基于通用生成函数的结构可靠性优化

蒋国盛, 周金宇, 朱达伟, 庄百亮

(1. 江苏理工学院机械工程学院, 江苏 常州 213001; 2. 金陵科技学院机电工程学院, 南京 211169;3. 机械科学研究总院江苏分院有限公司, 江苏 常州 213001)

可靠性优化设计是不确定性结构优化的主要途径, 可分为双循环法、单循环法和解耦法．双循环法是最直接的可靠性优化方法,于明等[1]通过双循环法将多学科优化与可靠性分析相结合,以离心式压气机叶轮为研究对象, 综合考虑环境和材料性能等随机因素的影响,提高了设计方案的准确性和可靠性．由于双循环法包含2个依次进行的循环过程, 计算效率较低,故研究人员在此基础上提出解耦法．解耦法的本质是将结构优化与可靠性分析分开, 将基于可靠性的优化问题转换为确定性序列的优化问题,从而提高计算效率．Yi等[2]对解耦法(sequential optimization and reliablity assessment, SORA)进行改进, 在可靠性评估中采用了近似最可能目标点和近似概率性能测度, 该方法比SORA和其他常用的可靠性优化方法效率高、鲁棒性强; Ho-Huu等[3]发现传统解耦法处理可靠性优化问题的最优结果依赖于初始点,故提出一种将SORA算法与改进的约束差分进化算法相结合的SORA-ICDE算法, 其具有全局搜索机制,提高了算法适用性．但双循环法和解耦法都是由优化循环和可靠性分析循环构成, 计算效率并无明显提高．为此,人们使用单循环法将可靠性分析过程用确定性约束条件代替．Mansour等[4]提出一种基于响应面法的单循环可靠性优化算法, 避开了最可能点, 具有较高的计算精度和效率．

通用生成函数(universal generating function, UGF)自1986年提出后便在可靠性领域得到广泛应用．21世纪初, 研究者提出了多种基于UGF的可靠性分析方法．Bisht等[5]提出一种利用UGF和欧文方法计算复杂桥梁网络的可靠性指标算法; 高贵兵等[6]为解决多状态系统组合爆炸问题, 提出了一种基于UGF的混流制造系统脆弱性量化评价方法; 刘成龙等[7]利用UGF对复合材料层进行可靠性分析,证明其适用于多变量、非线性、非正态功能函数结构系统．本文将通用生成函数引用到结构可靠性优化中, 通过k-means聚类[8-9]和同类项合并方法抑制组合爆炸的发生,提高高度非线性问题的计算精度和效率,为结构可靠性优化提供新的模型算法．

1 算法介绍

1.1 结构可靠性优化设计

结构可靠性优化设计的主要目的是在满足可靠性要求的条件下使目标函数最小或最大化．典型的可靠性优化设计模型[10-11]可表示为mind,μXf(d,μX,μP), s.t.Pr[Gi(d,P)≤0]≥R(i=1,2,…,n), 式中f为目标函数;d为确定性设计向量,X为随机设计变量的参数向量,P为随机不确定变量的参数向量,μX,μP分别表示为X,P的均值向量;Gi(d,P)≤0表示结构失效;Pr[]为失效概率向量;R为可靠性指标．

1.2 k-means聚类算法

1.3 基于UGF的结构可靠性优化流程

传统的可靠性优化设计在处理复杂的工程问题时,往往因非正态、非线性功能函数等因素出现计算效率低、精度不高等问题．故将UGF法引入结构可靠性优化中, 代替双循环法中的一次二阶矩法、二次二阶矩法以及蒙特卡罗法等传统算法,并在可靠性分析时加入k-means聚类和同类项合并以减少计算成本．图2为基于UGF的结构可靠性优化设计流程图,Uj表示结构系统的通用生成函数,Pab表示与性能值对应的概率值,gb表示随机变量的性能值,a,b分别为结构系统中的元件个数和元件状态的个数．

2 算例

2.1 数值算例

1) 线型极限功能函数数学模型．结构可靠性优化设计的数学模型为minf=m1+m2, s.t.Pr[g(M,T)≤0]≤Φ′(-β), 线性极限功能函数为g(M,T)=t1+t2+m1+m2, 式中M=(m1,m2)是设计变量的向量;T=(t1,t2)是随机变量的向量, 服从正态分布且相互独立;t1,t2的均值和标准差分别为[5, 3]和[1.5, 0.9]; 可靠度指标β为2.33;Φ′是可靠度指标转换系数．分别采用蒙特卡罗法、一次二阶矩法、二次二阶矩法以及UGF进行可靠性优化, 并以蒙特卡罗法的计算结果作为检测标准进行比较,优化结果见表1, 其中蒙特卡罗法的试验样本数为106, UGF(1), UGF(2), UGF(3)分别表示聚类后样本数为5, 10, 15的通用生成函数．由表1可知,UGF、一次二阶矩法、二次二阶矩法对于正态线性功能函数而言计算精度相近,但聚类后的样本数过少会影响UGF的计算精度．

表2 非线性极限功能函数模型的可靠性优化结果

2.2 工程实例

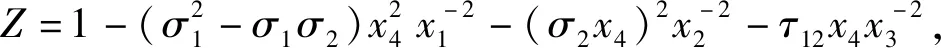
表3 复合材料层的可靠性优化结果

3 结论

基于通用生成函数的结构可靠性优化,相较于一次二阶矩法等传统可靠性方法,在解决非线性非正态问题时,依然保持较高的精度,具有广泛的适用性;相较于蒙特卡罗法,在保证精度的条件下,计算成本大幅度减少,具有良好的工程实用性．运用通用函数法进行结构可靠性优化时,通过同类项合并、k-means聚类算法简化计算,可抑制组合爆炸的发生,提高计算效率．