基于三维涡流场模型的变压器结构件损耗计算

周壮广，可欣荣，张建瓴

(华南农业大学 工程学院，广州 510642)

0 引言

配电变压器普遍应用在城市及农村电网中，实际使用负荷的情况不同，差异较大。配电网中出现的过载、三相不平衡、负载波动大、功率因数低等问题[1-3]，会导致变压器损耗增加，进而使变压器过热及运行效率低等问题日益凸显。在变压器研发、设计过程中，精确计算配电变压器在过载及低功率因数等运行状态下的结构件损耗，有助于提高其温度场和热点的计算精度，对提高变压器的运行可靠性、使用寿命及节能效果具有重要意义。

变压器结构件损耗的计算方法主要包括简化或经验公式法、有限元法(FEM)及间断伽辽金(DGM)等。文献[4-5]使用简化公式计算绕组损耗，提出了变压器热点计算的改进热路模型，但未考虑到过载时负载电压将随负载率的增大而减小；文献[6-7]在计算配电变压器的运行效率及经济性时，将有功功率损耗正比于负载率的平方和短路损耗，但该方法忽略了电压变化及功率因数的影响；文献[8]采用场路耦合的FEM法计算绕组电流及损耗，可以同时计及负载率及功率因数的影响，但实际电网中的等效负荷难以确定，考虑复杂运行工况时需解决系数矩阵不对称等问题；文献[9]在计算变压器涡流场时利用简化公式计算不同负载率下的绕组损耗，但该方法同样未考虑负载电流的精确计算及电压波动问题。

在实际工作中当变压器负载率和功率因数变化时，结构件的电磁损耗会发生改变。传统的损耗计算方法是将“额定负载电流负载率”作为负载电流，由于铁芯磁导率存在饱和现象，线圈电感随线圈电流变化，且变压器的外特性曲线是下降的[10](对感性负载而言)，计算出来的负载容量将与实际容量会存在一定差异，由此得到的变压器结构件损耗也将产生误差。特别是功率因数较低以及负载率较大时，因外特性曲线下降的幅度较大，误差就更大。因此在对铁心的电磁特性进行模拟计算的同时，有必要考虑负载电压对负载率及功率因数的影响，精确还原特定负载率下的负载容量，使计算得到的损耗值与实际运行情况更接近。

本文以S9-1600/10/0.4型配电变压器为例，提出了一种基于三维涡流场模型的变压器结构件损耗精确计算方法。首先用FEM计算变压器内部电磁场求得变压器外特性曲线，经数据拟合后得到变压器外特性曲线的一般表达式，由该表达式可求出不同功率因数和负载率下变压器的负载电流，再以此负载电流值作为三维涡流场模型中的电流激励，来计算变压器各结构件的损耗，并将此方法的计算结果与未修正的传统方法进行对比。

1 涡流场计算模型

1.1 材料模型及网格剖分

根据S9-1600/10/0.4型变压器的实际尺寸建立三维涡流场的几何模型，建模时忽略油箱外部散热器和拉板等，并将线圈设为均匀多匝线圈(几何体上表现为圆筒型)。绕组和油箱分别采用铜及合金钢。主要材料的电磁参数见表1。

表1 主要材料的电磁参数

图1所示为变压器的几何模型及网格剖分结果。其中，8级铁心采用扫略网格，按每级厚度分层扫略剖分；绕组为普通物理超细化剖分；夹件、变压器油和油箱为普通物理常规剖分。单元总数928 848个，以偏斜度为度量，平均单元质量为0.678 8 g。

图1 变压器几何模型和网格剖分图Fig.1 Transformer geometric model and mesh generation

将铁心等效为均匀铁心，并设y轴垂直于硅钢片轧制方向，x轴和z轴沿硅钢片轧制方向(见图1)，则铁心的电导率和磁导率张量分别为[11-12]：

(1)

(2)

其中，σ为叠片电导率，S·m-1；F为铁心叠积系数；a为叠片的宽度，mm；d为叠片厚度，mm；μfx，μfy和μfz分别为沿x，y和z方向的磁导率，H·m-1；μ0为真空磁导率，H·m-1。计算时，F取0.95，σ取4.3×106S·m-1，a为167 mm，d为0.3 mm，铁心沿轧制方向相对磁导率为4 000，垂直轧制方向相对磁导率为400。

1.2 场域方程与线圈模型

使用A-V-A法计算电磁场，在复频域中，铁心、夹件和油箱为导电涡流区，绕组及变压器油为非涡流区。频域似稳态下各求解域的控制方程为[13-15]：

(3)

式中，A为矢量磁位，Wb·m-1；V为标量电位，V；ω为角频率，rad·s-1；Je为绕组电流密度，A·m-2。电流密度Je由绕组实际相电流乘匝数后再除以绕组截面积求得。

S9-1600/10/0.4型变压器的额定参数见表2。该变压器的低压绕组由20条导线并绕，匝数14，单根导线截面积4.75 mm11.2 mm；高压绕组匝数367，单根导线截面积2.8 mm12.5 mm。由于模型设计的计算域为变压器的一半，因此计算中线圈的导线长度乘2，截面积不变。

变压器短路时，高压绕组施加短路电压，低压绕组短接。由于表2中的短路阻抗Uk是经换算到温度为75 ℃时的阻抗，计算时须将其还原到20 ℃时的值，此时高压线圈的各相激励电压可表示为：

(4)

其中，UAφ，UBφ和UCφ为高压绕组相电压，V；U1N为高压绕组额定线电压，V；s为温度修正系数，环境温度为20 ℃时，s=1.215 7。低压线圈短接，因此设置激励电压为零。由于连接组别为0，故低压三相电压相位与高压线圈相同。

变压器空载时，高压绕组施加额定电压，低压绕组开路。仿真计算时，高压绕组各相激励取额定相电压，相位相差120°。低压绕组三相激励电流均取为零。最后采用库仑规范对所有计算域添加矢量磁位A的散度约束。

1.3 约束条件

由于电磁场在油箱内表层的透入深度约为0.9 mm，而油箱厚度为10 mm，因此油箱的外表面可直接设为磁绝缘，同时也满足电绝缘条件。中间对称面采用磁绝缘边界条件。

根据变压器内部和外部的接地要求，铁心需要一点接地，铁心的接地点通过夹件与外壳连接，变压器外壳直接接地。仿真模型中直接指定接地点，该点处电位取为0，在铁心和夹件上分别取一点设为接地点，油箱上取一条长边接地。

2 短路及空载模型验证

在变压器短路及空载情况下对上述涡流场模型进行验证计算，计算频率设置为50 Hz，线圈几何参数采用MUMPS直接求解器，频域稳态下的线圈电流、场量A及V使用PRADISO直接求解器。

表3为短路时高、低压绕组线圈电流的计算结果。由表3可知，高低压绕组中B相电流幅值均小于A相和C相的电流幅值；高压绕组相电流的平均幅值与额定电流值的相对误差为7.218%，低压绕组相电流平均幅值与额定电流值的相对误差为7.214%。

短路时变压器各结构件损耗计算结果见表4。表中高低压绕组的损耗计算值是折算到75 ℃时的数值，短路时的总损耗额定值对应表2的短路损耗Ps。可以看出，短路时的总损耗计算值和额定值相比略有减小，相对误差为5.639%。

空载时变压器各结构件损耗计算结果见表4。表中空载时总损耗额定值对应表2的空载损耗P0。可以看出，空载时总损耗计算值和额定值相比稍小，相对误差为0.713 4%。而且，空载时损耗主要集中在铁心上，铁心损耗占到了总损耗的99.71%。

表2 S9-1 600/10/0.4型变压器的额定参数

表3 短路时各线圈电流幅值计算结果

表4 短路和空载时变压器损耗计算结果

表5 空载时高压绕组电流和低压绕组电压幅值计算结果

表5为空载时高压线圈各相电流幅值和低压线圈各相电压幅值的计算结果。空载时，低压绕组电压应为额定电压，高压绕组线圈电流应为空载电流，由表5可知，空载时高压绕组中B相绕组的电流幅值明显小于A，C两相的电流幅值，电流平均值与额定值的相对误差为0.651%。低压绕组各相电压与额定值的相对误差均为0.026%。

上述计算结果表明文中所建立的三维涡流场计算模型在短路、空载时的绕组电流、电压和损耗计算中具有较高精度，说明模型中电磁材料模型及线圈模型等是合理的，能满足工程计算的精度要求。

3 外特性曲线及结构件损耗计算

3.1 外特性曲线的一般表达式

变压器带负载时，一次绕组施加额定相电压激励，二次侧施加相电流激励，通过改变相电流大小算出不同负载电流下二次侧相电压，即可得到变压器的外特性曲线。考虑到变压器的连接组别，高压和低压绕组相电压的相位差为零，而低压侧相电流的相位由负载功率因数决定。因此，对感性负载而言，低压线圈施加的相电流激励可表示为：

(5)

式中，Iaφ，Ibφ和Icφ为低压绕组相电流，A；SN为变压器额定容量，kV·A；Lv为负载电流倍数；θ为功率因数角，rad；N1，N2分别为高压、低压绕组匝数。由于匝数比不等于25，因此模拟计算时以高压绕组电流为基准来计算低压绕组电流，高压线圈施加额定相电压激励。

计算中假设变压器绕组的温度为75 ℃，因此须将线圈导线的电导率换算到75 ℃时的电导率(4.947 8107S·m-1)。负载电流倍数Lv分别取0.25，0.50，0.75，1.00，1.25和1.50，利用涡流场模型分别计算不同功率因数时的二次侧相电压幅值的平均值，可得到变压器的外特性曲线如图2所示。由于模拟计算中铁心材料模型为线性模型，故外特性曲线为近似线性，对外特性曲线进行线性拟合，结果如表6所示，表中Uav和Iav分别为低压绕组相电压及相电流幅值的平均值，k为直线的斜率，b为空载时相电压幅值的平均值。

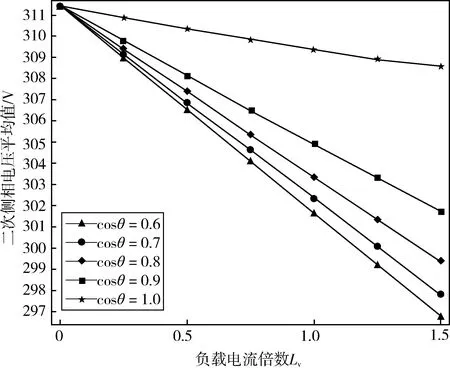
图2 不同功率因素下的外特性曲线Fig.2 Transformer external characteristic curves at different power factors

表6 变压器外特性曲线拟合结果

由图2和表6可知，随着功率因数减小，外特性曲线的倾斜程度变大，即二次侧相电压下降幅度加快。斜率k主要与功率因素有关，将k随cosθ变化的数据进行拟合可得：

k(cosθ)=0.063 9·(cosθ)3-0.136 2·(cosθ)2+0.098 4·(cosθ)-0.026 6 .

(6)

其中，k(cosθ)表示k为cosθ的函数。则二次侧相电压幅值可表示为相电流幅值Iav及功率因素cosθ的函数关系：

Uav=k(cosθ)·Iav+b.

(7)

式(7)即为变压器外特性曲线的一般表达式。

变压器实际运行时，负载率L的计算公式为：

(8)

其中，S为实际负载容量，kV·A；Uaφ，Ubφ和Ucφ为二次侧相电压幅值，V。假设变压器三相的负载相同，依据式(7)和(8)可得：

[k(cosθ)·Iav+b]·Iav=2L·SN/3 .

(9)

由上式可求解变压器在不同功率因数及负载率下的负载电流幅值Iav(平均值)，将其带入三维涡流场模型即可计算各结构件的损耗。

3.2 结构件损耗计算结果及分析

表7为功率因数cosθ=0.6时不同负载率下变压器低压绕组各相的负载容量平均值。表中的标准值为三相额定容量平均值与负载率的乘积；未修正值是将“负载额定电流负载率”作为负载电流时(利用三维涡流场模型)求得的负载容量；修正值是将式(9)计算求得的Iav作为负载电流时(利用三维涡流场模型)求得的负载容量。由表7可知，未修正时负载容量与标准值的相对误差随负载率的增大而增大，最大相对误差为4.725%。而利用Iav计算得到的负载容量与标准值的相对误差明显更小。

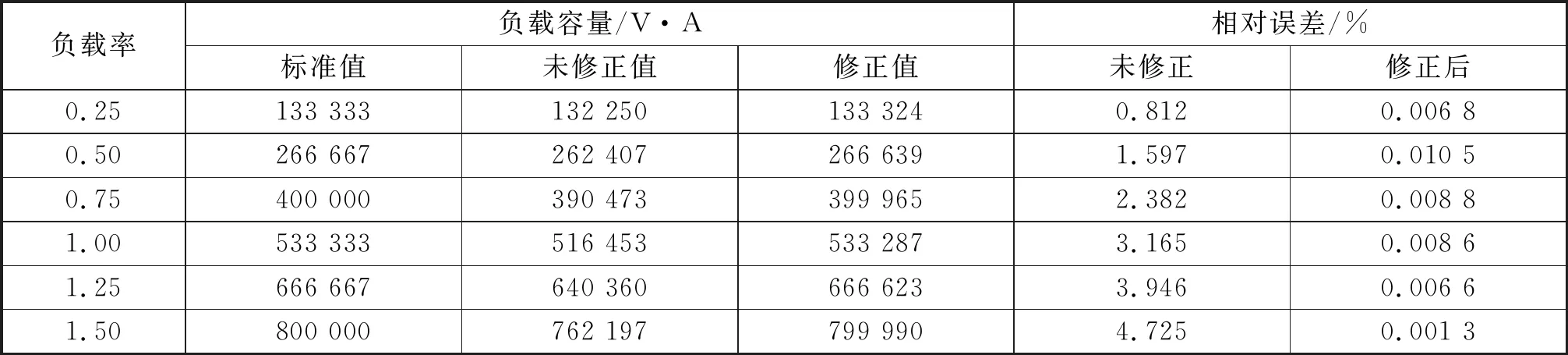
表7 功率因素为cosθ=0.6时负载容量计算结果

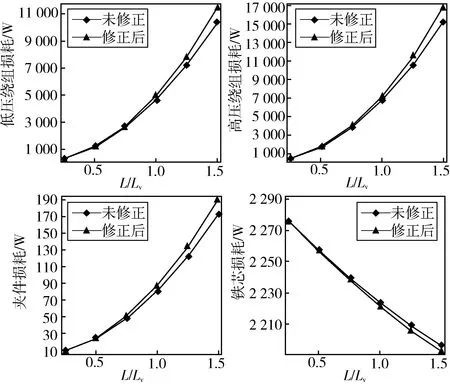
图3 功率因素cosθ=0.6时变压器各结构件损耗计算结果Fig.3 Calculation results of structural parts loss at cos θ=0.6

图3至图5分别为功率因数取0.6，0.8和1.0时，由三维涡流场模型计算的变压器各结构件损耗随负载率L(或负载电流倍数Lv)的变化规律。图中未修正值是将“负载额定电流负载率”作为负载电流时 (利用三维涡流场模型)求得的损耗值，修正值是将Iav作为负载电流时 (利用涡流场模型)求得的损耗值。可以看出，相对于铁心和夹件损耗来说，高低压绕组损耗受功率因素和负载率的影响较大；在一定功率因数下，高低压绕组和夹件损耗随负载率的增加而变大，铁心损耗则稍微减小。

由图3至图5也可以看出，利用Iav求得的高低压绕组和夹件损耗值相比传统计算方法得到的损耗值都有一定程度增加，而铁心损耗则略有减少，且随着负载率的增加其差异变大。例如功率因数0.6和负载率1.50时(图3)，低压绕组修正后损耗相比未修正损耗增大了1 117.52 W，增幅10.73%；高压绕组损耗增大了1 622.68 W，增幅10.67%；夹件损耗增大了17.70 W，增幅10.25%；铁心损耗则减小了3.72 W，减幅0.17%。当功率因数较大或负载率较小时，修正前后损耗计算值差异较小。例如功率因数取1.0及负载率取1.50时(图5)，低压绕组修正后损耗相对于未修正值增大了198.28 W，增幅1.90%；高压绕组损耗增大了285.98 W，增幅1.90%；夹件损耗增大了3.10 W，增幅1.84%；铁心损耗只减小了0.1 W。

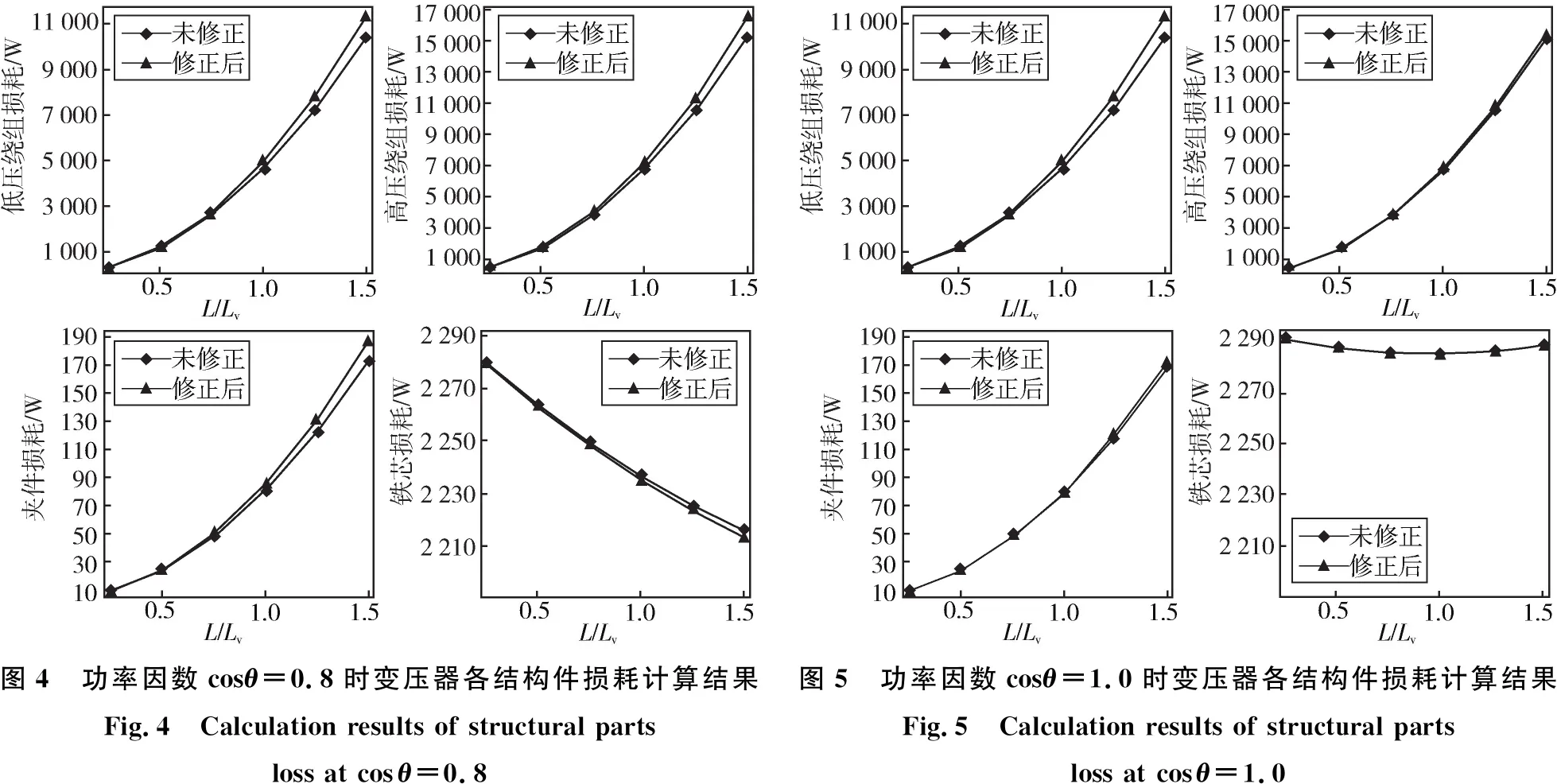
图4 功率因数cosθ=0.8时变压器各结构件损耗计算结果Fig.4 Calculation results of structural parts loss at cosθ=0.8图5 功率因数cosθ=1.0时变压器各结构件损耗计算结果Fig.5 Calculation results of structural parts loss at cosθ=1.0

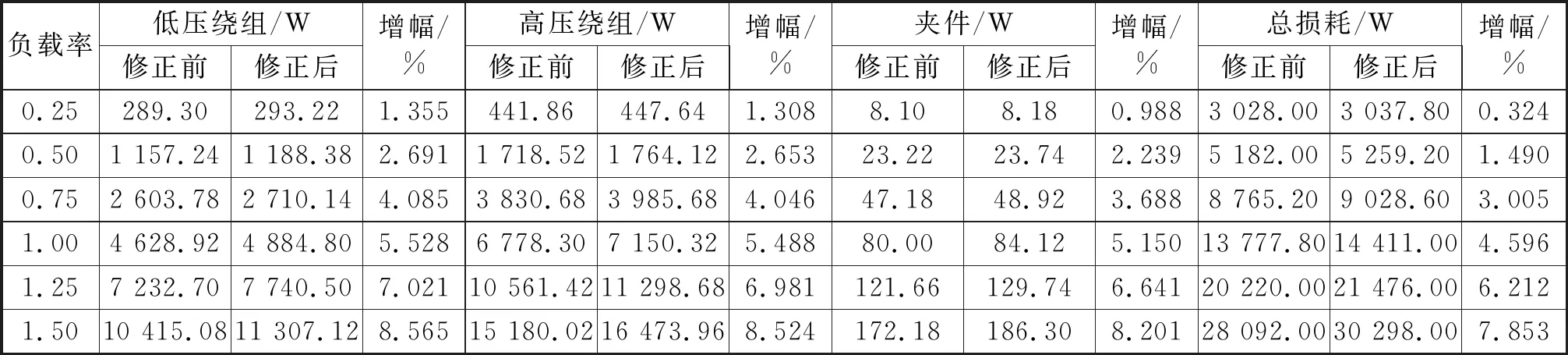
表8 功率因数cosθ=0.8时变压器损耗模拟计算结果

4 结论

本文利用Comsol软件建立了S9-1600/10/0.4型变压器的三维涡流场模型，并对该模型在变压器空载及短路情况下的计算精度进行了验证。在此基础上，提出了一种基于三维涡流场模型的变压器损耗精确计算方法，即利用三维涡流场模型计算得到变压器外特性曲线的一般表达式，由此求出变压器在不同功率因数和负载率下的负载电流，将此负载电流作为三维涡流场模型中的线圈电流激励，再计算变压器各结构件的损耗。该方法可以方便计算任意功率因数、任意负载率下变压器结构件的损耗，且由于考虑了实际负载电压随负载电流变化的因素，与传统损耗计算方法(文献[4]—[7]和[9])相比具有更高的精度和准确性。仿真算例的计算结果表明，在功率因数较小及负载率较大时，由本文方法计算得到的变压器损耗值和未修正的传统计算方法得到的损耗值之间存在较大差异；在功率因数较大及负载率较小时其差异不明显。在变压器研发设计过程中，对于设备可能运行在过载及低功率因数的情况，有必要考虑这种差异。