基于斑点鬣狗算法的风/光/抽水蓄能联合运行系统优化调度研究
2020-05-27张志浩黄泰相付翊航
钟 文,张志浩,管 鑫,陈 波,黄泰相,付翊航
(1.国网荆门供电公司,湖北 荆门 448000;2.国网湖北直流运检公司,湖北 宜昌 443002)
0 引言
为了解决分布式能源发电给电力系统带来的冲击问题,国内外学者们将目光投向了抽水蓄能电站与新能源发电协同合作上,将抽水蓄能电站作为新能源电站与电力系统中间的调节工具:当电力系统中的负荷曲线处于波谷时,抽水蓄能电站能够将电力系统和新能源发电中的多余电量转化为重力势能储存起来;当电力系统负荷曲线处于波峰时,抽水蓄能电站能够出力对波峰负荷进行补偿。用这一方式实现削峰填谷,解决新能源发电入网给电力系统带来的冲击问题,同时也改善了电力系统的运行环境[1,2]。
目前,诸多学者关于抽水蓄能电站与新能源发电协调运行的研究多集中在联合系统数学模型的建立,以及电网运行的经济效益方面。文献[3]建立风电与抽水蓄能电站协同运行的双目标优化模型,以最大化联合体的效益和平滑联合体的出力为目标,并通过多目标克隆选择算法求解模型。文献[4]等研究了传统火电站与抽水蓄能电站的联合运行系统,通过抽水蓄能电站的配合运行,减小传统火电站的运行成本,建立两者联合运行的优化模型。文献[5]研究了发电机组中含抽水蓄能机组的运行优化问题,并对比分析了不同的模型求解算法的优缺点和适用范畴。文献[6]对风力发电与抽水蓄能电站联合运行方式进行了研究,建立了相关的数学模型进行仿真分析。文献[7]在建立风能和抽水蓄能联合模型时,将电力系统中的运行工况和设备状态考虑在内,进一步完善了联合系统的数学模型。
本文拟建立抽水蓄能电站与新能源发电联合运行系统的数学模型,模型在考虑联合系统经济收益的同时,要求多种因素综合考虑最优,采用斑点鬣狗算法对模型进行求解。与应用最广泛的遗传算法、蚁群算法和粒子群算法等相比,斑点鬣狗算法具有较好的鲁棒性的同时,还拥有极快的搜索速度,并且没有陷入局部最优解的缺点。
1 联合发电系统并网分析
1.1 联合系统数学模型
在建立联合系统目标函数时,不仅需要考虑到联合系统的经济收益,还应考虑到系统对风能、太阳能的利用率,系统自身的能源损耗,对电力系统的运行影响,减少传统能源的污染排放量等,并且要多种因素综合考虑最优[8]。为了建立环境友好型的联合优化系统,本文在建立目标函数时考虑在联合系统运行时,以风能和太阳能发电出力最多为基础,即要求整个电力系统在最大程度上减少煤电消耗(或者说煤电消耗最小),同时合理控制剩余电量的调度分配,于是得到模型的目标函数为:
(1)
式中,F表示系统中的煤电消耗量,取得F最小时为最优结果;i表示系统中火电机组的台数;Mit表示第i台火电机组在t时刻的煤耗总量;mi表示第i台火电机组在启动或停运时的煤耗;ci表示周期内该台机组的启停变换次数。
1.1.1 系统功率平衡
在联合系统并网运行时,最基本的约束条件就是系统的功率能平衡,即要求任意时刻各类电源的发电量总和等于所有负荷的需求量总和,得到以下约束方程:
Pc(t)+Ph(t)+PW(t)+PS(t)=PLD(t)+Pp(t) .
(2)
式中,Pc(t)为传统电厂的输出功率,Ph(t)为抽水蓄能电站输出功率,PW(t)为风力发电输出功率,PS(t)为太阳能发电输出功率,PLD(t)为电力系统原有负荷,Pp(t)为抽水蓄能时水泵和电机的消耗的功率。
1.1.2 电网运行的包容性
电力系统在运行的过程中长期保持着动态平衡,新能源发电系统在电力系统中频繁的投退会对电力系统的安全运行造成一定威胁,如果随机投退的电源容量超过一定范围时,将超过电网运行的包容度,无法达到稳定运行的状态。因此,要求联合系统在电力系统中的输出功率能够在电网运行包容度范围内,本文设定联合系统中不稳定输出(风能和太阳能发电)的功率达到负载功率的20%时,将超出电网运行包容度,于是得到以下约束方程:
Ps,out+Pw,out≤0.2PLD.
(3)
式中,Ps,out表示太阳能发电并网功率,Pw,out表示风能并网功率。
1.1.3 电网能量传输限制
通常,风力发电场和光伏电站等电源安装在离市区较远的地方,一般需要架设专门的输电线路进行能量传输。在架设线路时需要考虑设备利用成本,因此其传输容量是有一定限制的,所以在风能和太阳能向电网输送能量时,会受到架空输电线路的能量传输限制,于是得到以下约束方程:
Pmin≤Ps,out+Pw,out≤Pmax.
(4)
式中,Pmin和Pmax分别表示架空线路正常工作时的最小传输功率和最大传输功率。
1.1.4 抽水蓄能电站机组约束
通常认为抽水蓄能电站不能同时工作在两种模式下,即不能在抽水蓄能期间启动水轮机组发电,同理也不能在发电时进行抽水蓄能。由此可得以下约束方程:
(5)
ρ(t)∈{0,1} .
(6)
0≤Ph(t)≤ρ(t)·Ph,max(t)·Nhp.
(7)
np(t)Pp,min≤Pp(t)≤np(t)Pp,max.
(8)
np(t)≤Nhp.
(9)
(10)
np(t+1)=np(t)+nsu(t+1)-nsd(t+1) .
(11)
式中:Nhp为抽水蓄能电站同型号的抽水-发电机组数目;Pp,max,Pp,min为水泵抽水功率上、下限;ρ(t)的值为1时表示机组出力在发电状态,值为0时表示其处于水泵抽水状态;np(t)为t时段工作的水泵总数;nsu(t)和nsd(t)为t时段启/停水泵机组台数。
1.1.5 水资源约束
水库中的水量是相对恒定的,在进行抽水蓄能或是水力发电时,需要保证上水库或下水库的蓄水量保持在允许范围内,于是得到以下约束方程:
Vu(t)=Vu(t-Δt)+fup(Pp(t),H(t))-fdown(Ph(t),H(t)) .
(12)
Vu(t)=Vd(t-Δt)-fup(Pp(t),H(t))+fdown(Ph(t),H(t)) .
(13)
Vu,min≤Vu(t)≤Vu,max.
(14)
Vd,min≤Vd(t)≤Vd,max.
(15)
式中,Vu(t),Vd(t)分别表示上、下水库中的蓄水量;Vu(t-Δt),Vd(t-Δt)分别表示上、下水库中t时刻变化前的蓄水量;fup(Pp(t),H(t))为以抽水功率和扬程为自变量的向上抽水流量函数;fdown(Ph(t),H(t))为以发电功率和水头为自变量的向下放水流量函数;Vu,min,Vd,min分别表示上、下水库中能储存的最少水量;Vu,max,Vd,max分别表示上、下水库中能储存的最多水量。
1.1.6 各类能源出力约束
在电力系统中的各类发电能源中,每一类能源均受其发电能力的限制,即各类能源发电量要求在对应机组发电能力的上限值和下限值之间,于是得到以下约束方程:
(16)
通常,在建立一个系统的数学模型时,给定的约束条件越完善,越能够真实说明实际情况,但随着约束条件的增多,所建立的数学模型复杂度也会增加,求解速度和难度进一步加大。在本文中选择了以上几个约束条件对实际模型进行简化,在抓住模型中主要影响因素的同时,尽量简化和忽略其他次要的影响因素。
在对基于风光互补的抽水蓄能电站的数学模型进行分析时,选择何种求解方法是一个讨论度很高的问题。在精确的数学模型下,求解问题显得更加棘手,容易出现维数过高、计算量巨大、计算速度慢、计算结果出现偏差等诸多问题。为了解决计算数学模型过程中存在的以上问题,学者们研究了多种智能算法来进行求解。这些算法的计算原理基本一致:通过计算机应用不同的筛选策略在所有的可行解中寻求最优解,其中应用较为广泛的有遗传算法、蚁群算法和粒子群算法等。遗传算法和蚁群算法在面对多约束和高维度的数学模型求最优问题时具有较好的全局优化性和鲁棒性;粒子群算法在具有较好的鲁棒性的同时,还拥有极快的搜索速度,但其缺点是容易陷入局部最优解。本文已建立较为简化的数学模型,在了解了以上算法模型后,决定选用斑点鬣狗算法来进行模型的求解分析。
1.2 斑点鬣狗算法
斑点鬣狗的行为可以简化为搜索、包围、狩猎和攻击猎物。建立粘性集群有助于斑点鬣狗之间的有效合作,也最大限度地提高适应性。本节对斑点鬣狗的狩猎技术和社会关系进行数学建模。这种行为的数学模型可由以下方程式表示:
(17)
(18)
(19)
(20)
(21)
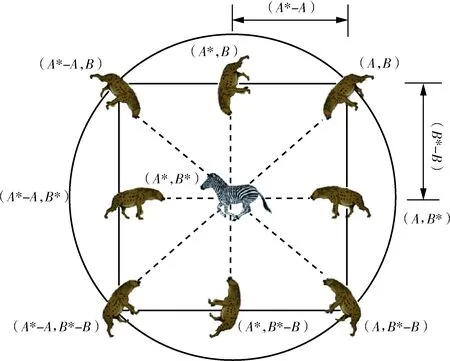
图1 斑点鬣狗的二维位置矢量Fig.1 Two-dimensional position vector of spotted hyena
斑点鬣狗是群居动物,通常依靠朋友间的信任关系和识别猎物位置的能力来捕猎。为了从数学上定义斑点鬣狗的行为,假设每一只斑点鬣狗都知道猎物的位置,斑点鬣狗组成一个集群向猎物的位置靠近,并留下到目前为止最好的狩猎路径来更新它们的位置。该行为可以用公式表示如下:
(22)
(23)
(24)
(25)
(26)
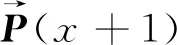
斑点鬣狗可以熟悉猎物的位置并包围它们。为了对斑点鬣狗的社会等级进行数学建模,我们认为目前的最佳候选解决方案是目标猎物或最优斑点鬣狗的位置,因为搜索空间先前未知,所以搜索时需不断接近最优。其他搜索代理将在定义最佳搜索候选解决方案后尝试更新其位置,以获得最佳候选解决方案。
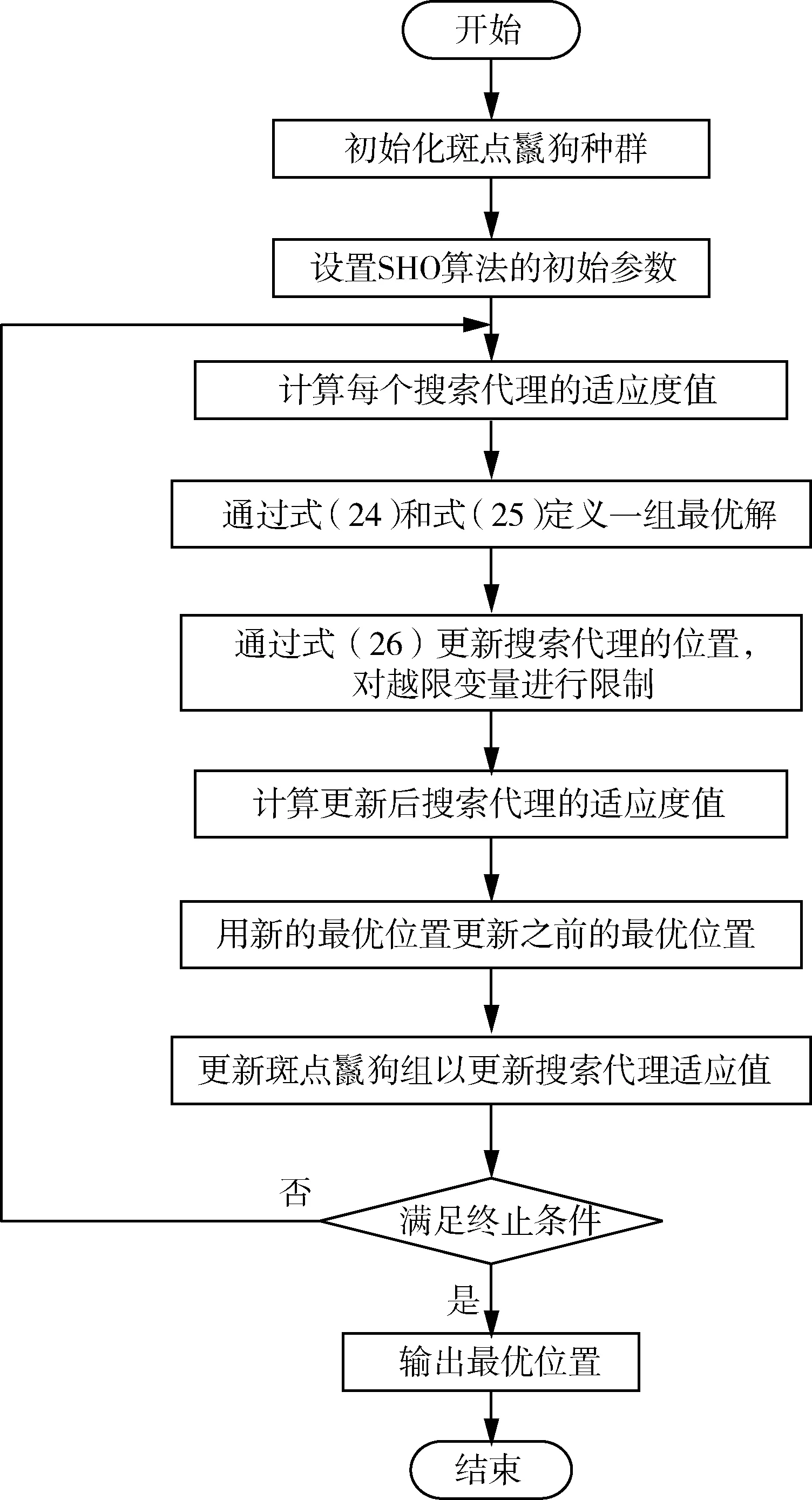
图2 联合系统优化调度算法流程图Fig.2 Flow chart of joint system optimization scheduling algorithm
用SHO算法解决优化问题时需要注意以下几点:
(1)该算法保留了迭代过程中获得的所有最佳解。
(2)所提出的斑点鬣狗搜寻机制定义了一个圆形的邻域周围的解决方案,可以扩展到更高的维度作为一个超球体。
(4)建议的狩猎方法允许候选解确定猎物的可能位置。
1.3 模型的求解
应用斑点鬣狗算法对风光抽水蓄能联合运行系统优化调度模型进行求解,其具体步骤如下,对应的流程图如图2所示。
(1)初始化种群。即产生符合式(2)-式(16)的初始值作为斑点鬣狗的初始位置;
(2)初始化参数。加载联合运行系统中各元件的参数(包括负荷曲线与可再生能源发电的输出功率曲线),确定能量调度策略,定义决策变量,设置种群规模和最大迭代次数等;
(3)评估适应度(目标)函数。计算每只斑点鬣狗对应的目标函数值;
(4)在给定的搜索空间中探索最佳搜索代理;
(5)定义一组最优解,即使用式(24)和式(25)直到找到满意的结果;
(6)使用式(26)更新搜索代理的位置;
(7)检查给定搜索空间中是否有搜索代理超出边界,并进行调整;
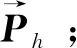
(10)迭代终止条件。重复步骤(5)—步骤(9)直至达到最大迭代次数时,最优目标函数值对应的位置即为决策解。
2 算例分析
2.1 模型参数设计
2.1.1 火电站参数设计
在对本模型参数进行设计时,参考我国某地区实际电网的模型,进行一定比例的负荷缩小和系统简化,得到本系统中的各项参数[9,10]。在本系统中,新能源发电量占总发电容量的10%,其余的发电量来自火电机组发电,火电机组容量取200 MW以下、300 MW以上、600 MW以上、1 000 MW四个等级,各等级机组台数占到火电总机组台数的15%,20%,25%和40%,机组的各项参数和性能如表1所示[11]。
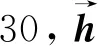
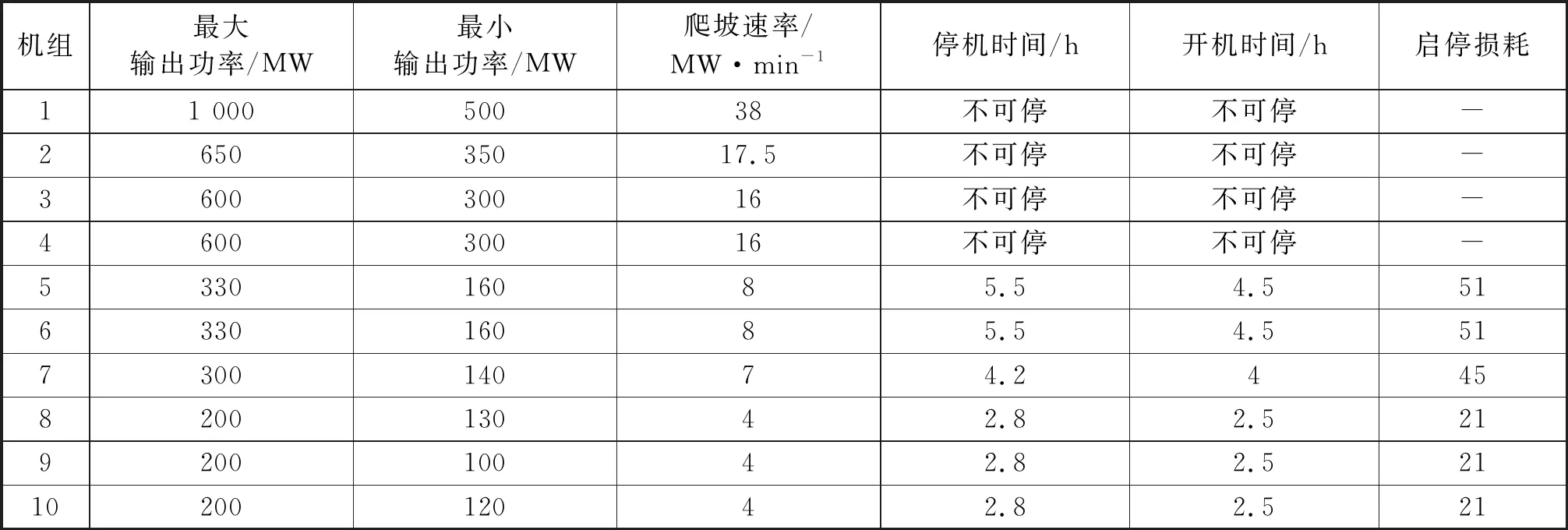
表1 火电机组参数与性能
经查阅相关资料,得知火电机组的煤炭消耗量可以按照以下公式进行计算。
在1 000 MW等级及以上容量的机组中,煤耗量可表示为:
(27)
在600 MW等级及以上容量的机组中,煤耗量可表示为:
(28)
在300 MW等级及以上容量的机组中,煤耗量可表示为:
(29)
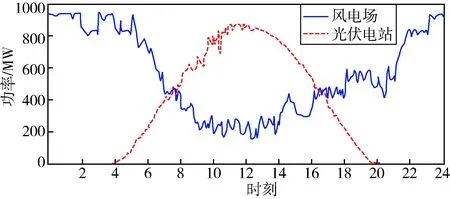
图3 风电场与光伏电站的出力情况Fig.3 Output of wind farm and photovoltaic power plants
在200 MW等级及以上容量的机组中,煤耗量可表示为:
(30)
上式中的La表示为火电机组的实际有功功率出力值。
2.1.2 风电场与光伏电站参数设计
如图3所示为模型中风力发电场和光伏电站的出力情况,其中虚线表示设计模型中的光伏电站的输出功率曲线,在中午12点时到达功率输出最大点,夜晚8点至次日凌晨4点输出为0;实线表示设计模型中的风电场的输出功率曲线,输出功率在凌晨时分达到最高峰,中午到达最低谷。
2.1.3 抽水蓄能电站的参数设计
在对抽水蓄能电站进行设计时,预设上水库的容量为3.6×106m3,不考虑下水库的水容量限制问题,抽水蓄能电站的机组参数如表2所示。
此外,对系统的其他要求进行规定:
(1)联合系统对外输送功率限制,输送功率最大值为780 MW,输送功率最小值为180 MW。
(2)本地电力系统允许电源变动率占负荷总量的15%。
(3)电力系统的运行频率在59.9~60.1 Hz的范围内波动。
(4)所有供电电源的容量总和应符合所有负荷大小的需求,偏差值应在1%以内。
2.2 风光协同并网系统的算例分析
为了与基于风光互补的抽水蓄能电站联合系统进行对比分析,首先进行了风光协同并网系统的仿真分析[12-13]。在风光协同并网系统中,由于缺少了抽水蓄能电站的能量存储作用,当风能与太阳能的发电量超过了输电线路的最大功率输送能力时,不得不弃用多余的发电量,增大了系统的弃风和弃光量。同时由于太阳能和风力发电具有不稳定性,系统中可靠的负荷调节仅可依靠火电机组来进行。
如图4所示是根据仿真结果得到的风光协同并网系统火电机组出力图,图中负荷基础部分功率由大容量机组提供,可以看出图中所圈部分出力较为稳定,大型机组通常保持在额定的范围内工作,仅在负荷最低点时进行了输出功率下调,在出力图标的上部分由小容量机组构成,通过控制小容量机组的出力和投退,来进行负荷调节,满足供电需求。图中可以看出,凌晨4:00—5:00和上午10:00—11:00期间,大容量机组参与了调峰出力,其他时候一般由小容量机组出力进行调整。0:00—8:00间,多个小型机组退出运行,增大了火电站的运行负担和电机启停损耗。
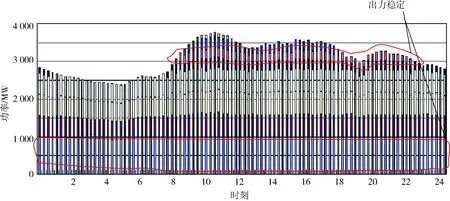
图4 风光协同并网系统火电机组出力时刻图Fig.4 Wind-solar coordinated grid-connected thermal power unit output schedule
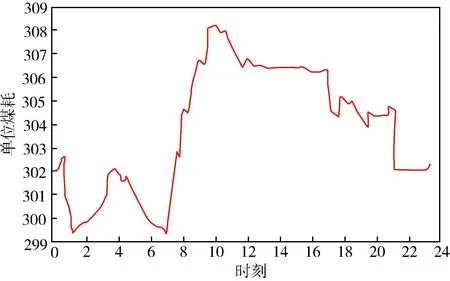
图5 火电机组平均单位煤耗Fig.5 Average unit coal consumption of thermal power units
如图5所示为风光协同并网系统中的火电机组平均单位煤耗,它反映的是在某一时刻,系统中煤炭资源的消耗总数与发电量之间的比值,平均单位煤耗越高表明对煤炭的利用率越低,平均单位煤耗越低则对煤炭的利用率越高。结合机组的投退情况,从图中的单位煤耗量可以看出,大机组参与负荷调压会使得机组的单位煤耗迅速增加。
根据以上的仿真结果可以看出,风光协同并网系统虽然在一定程度上弥补了单一的风力发电或太阳能发电出力的峰谷落差,但仍然是一个不稳定的系统,无法进行稳定的负荷补偿,在电力系统的峰谷补偿上并不能大规模减少火电机组的投退情况,从而降低系统损耗。因此接下来考虑在风光互补系统中加入抽水蓄能电站的情况。
2.3 加入抽水蓄能系统的算例分析
根据本文的理论研究部分,抽水蓄能电站能够减缓新能源发电的不确定性给电力系统带来的冲击,参与电力系统负荷曲线的峰谷调节,减少新能源发电的弃风和弃光率,从而有效提高光伏发电和风力发电的能源利用率,减少电网运行成本,减少传统火电站的煤炭能源消耗。下面对以上理论进行仿真验证。
如图6所示为加入抽水蓄能系统后的电网火电机组出力时刻图,从图中可以看出,大容量机组的输出功率较为平稳,但仍然参与部分负荷调节。在8:00—12:00的波峰区间内,可以明显看出加入抽水蓄能系统后,火电机组的出力减少了,且相较于加入抽水蓄能前其在波峰处更为平缓,验证了前文所述的抽水蓄能电站对电力系统的峰谷调节作用,同时减少了火电机组的输出和煤炭的消耗。
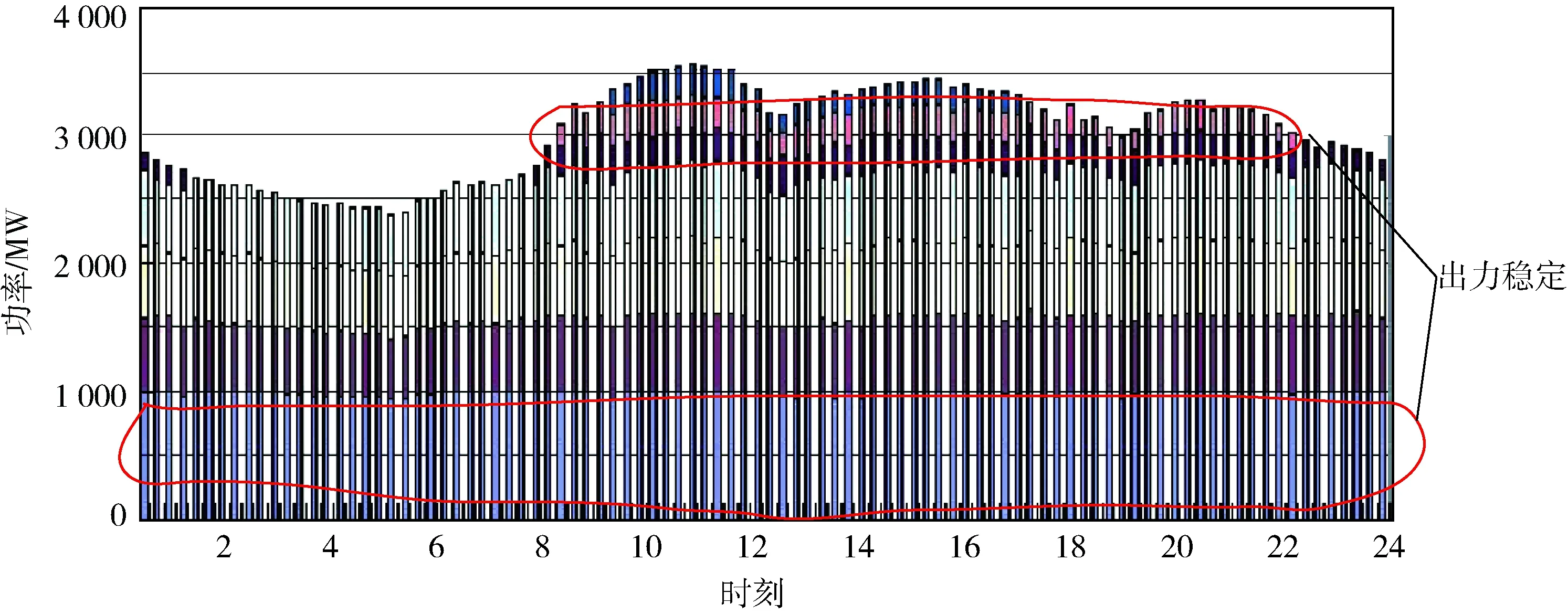
图6 加入抽水蓄能系统后的电网火电机组出力时刻图Fig.6 Power grid thermal power unit output schedule after adding pumped storage system
如图7、图8所示为抽水储能电站的上水库中的水量曲线和对外的输出功率图标。对比系统中火力发电机组的输出进行分析:在夜间的时候,上水库的水量逐渐增多,此时对外输出功率为负值,抽水蓄能电站吸收火电机组的额外输出功率,减少了火电机组退出运行的次数和频率;在白天负荷高峰时,上水库的水量减少,水能通过水轮机转换为电能,来填补电力系统中的电源缺额,也减少了火电机组投入运行的次数和频率。
因此,在风光协同并网系统中加入抽水蓄能电站后,整个系统能够在电力系统中充当额外的备用电源,同时也能够对电力负荷曲线进行削峰填谷,减少火电机组频繁投退造成的经济损失和能源消耗。
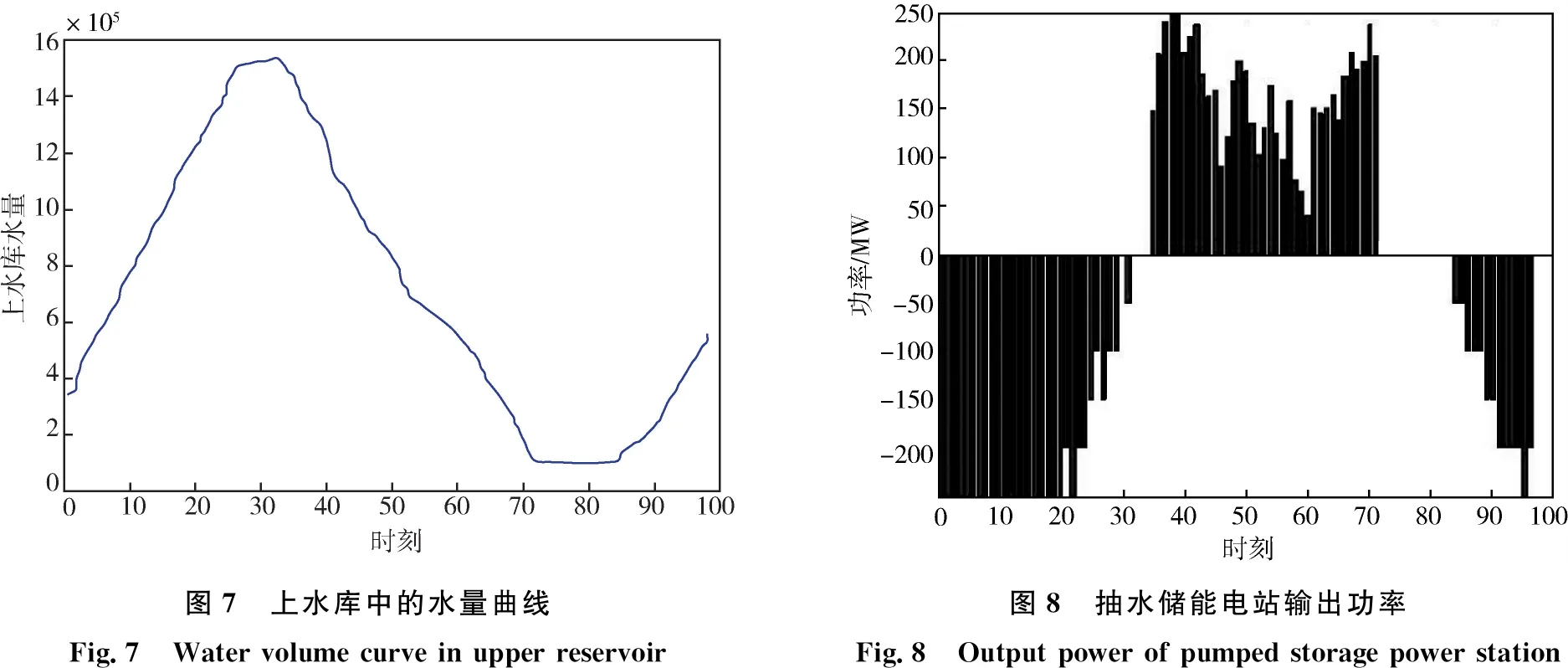
图7 上水库中的水量曲线Fig.7 Water volume curve in upper reservoir图8 抽水储能电站输出功率Fig.8 Output power of pumped storage power station
2.4 收益分析
2.4.1 增加发电量
基于风光互补的抽水蓄能电站,能够为电力系统提供大量的电能,将太阳能和风能通过电站转换为电能并入电力系统中。区别于单独运行的风力发电站和太阳能电站,联合系统能够将传输线路接受程度以外的能量进行储存,转换为水的势能作为备用电源,提高了能源利用率,减少了弃风和弃光现象。在提供能量的同时也相对应地减少了煤炭的使用量和对环境的污染。
2.4.2 削峰填谷
抽水蓄能电站作为缓冲系统,能够在需要的时候进行能量的储能和释放。一方面储存太阳能和风能的额外发电量,另一方面在电力系统负荷较轻的时候储存发电机组多出的输出功率。当电力系统中的负荷较重时,抽水蓄能电站能够将储存的能量向电网传输,以弥补当前机组输出容量不足的情况。在这个过程中,抽水蓄能电站对电力负荷曲线起到了削峰填谷的作用,同时也减少了火电机组频繁投退的现象。
2.4.3 增加最大发电容量
在现有的火电机组的基础上加入联合运行系统,新增加了风力发电机组、光伏发电机组、抽水蓄能机组等多个发电设备,大大增加了电力系统中的最大发电容量。电力系统中的容量裕度得到了增加,安全运行系数也能得到相应的提高。
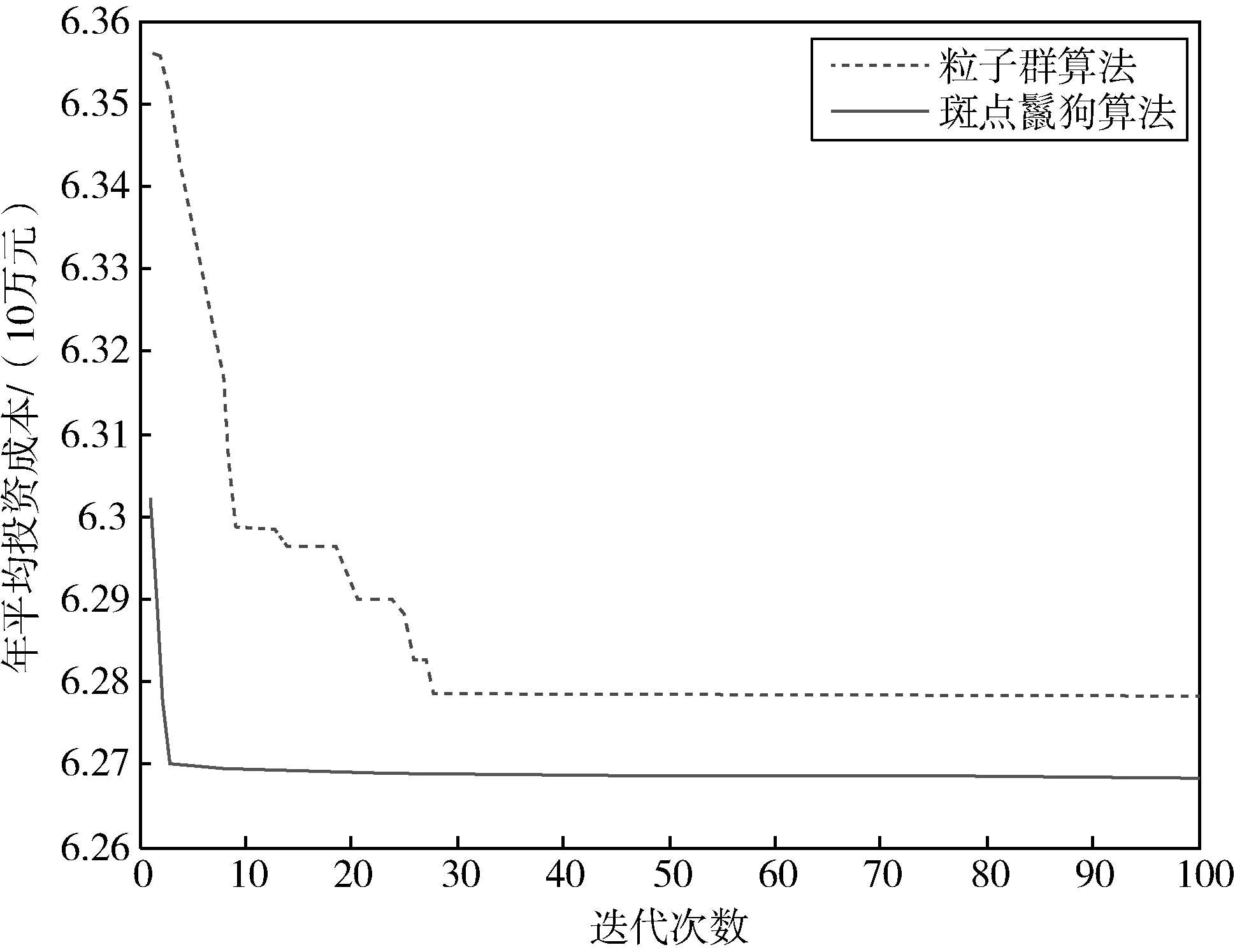
图9 斑点鬣狗算法和粒子群算法的收敛曲线Fig.9 Convergence curves of spotted hyena algorithm and particle swarm algorithm
2.5 斑点鬣狗算法与粒子群算法对比
考虑1.1节中的目标函数,分别使用斑点鬣狗算法和粒子群算法对上述算例进行求解。两种算法的收敛曲线如图9所示。
由图9可知,斑点鬣狗算法的全局寻优能力及收敛速度均优于粒子群算法。
3 总结与展望
基于风光互补的抽水蓄能电站联合运行系统在时间上和空间上都具有一定的互补性,从而提高了新能源发电的利用率,减少弃风弃光率,其削峰填谷效果亦有利于系统安全稳定的运行。基于此,本文做出了以下工作:
(1)构建出基于风光互补的抽水蓄能电站联合调度模型,确定其目标函数和约束条件;
(2)介绍了斑点鬣狗从生物行为衍变为优化算法的过程,期望通过斑点鬣狗算法来求解联合系统的数学模型;
(3)搭建了联合运行系统的模型仿真,对比分析了风光协同并网系统和加入抽水蓄能后的系统运行情况,仿真结果说明了基于风光互补的抽水蓄能电站带来的收益更有优势。
