基于改进粒子群优化LS-SVM的短期风速预测

范曼萍，周 冬

(三峡大学 电气与新能源学院，湖北 宜昌 443000)

近年来，随着我国对新能源的大幅开发，风电入网负荷正在逐年增加，清洁的风能在被人类利用的同时，也一定程度上影响了电力系统的稳定性[1]。自然风具有很大的随机波动性，风电在并入主网时，容易引起电压波形畸变、频率降低，影响电能质量，不利于电力系统的正常调度[2-3]。因此，及时掌握风速变化规律，做好风速预测工作，对电力系统调度计划的制定具有重要意义。

目前，智能算法在短期风速预测方面应用广泛，主要包括极限学习机、小波神经网络、卡尔曼滤波和支持向量机等[4-5]。文献[6]根据粗糙集理论，对风速预测的样本数据进行主成分分析，选取特征向量优化Elman的输入，进行了短期风速预测，该方法虽在一定程度上提高了风速预测精度，但所需样本容量太大，实用性不强。文献[7]根据小波变换理论，采用不同的方法分别对风速时间序列的近似分量和细节分量进行了计算，提出了一种风速组合预测方法。该方法只考虑了风速的时间特性，忽略了其他因素的影响。文献[8]通过对风速时间序列进行处理，采用传统粒子群(PSO)算法对LS-SVM参数进行优化，建立了短期风速预测模型，预测结果显示，该方法明显优于神经网络，但传统粒子群算法的粒子搜索方向性较差，该模型参数寻优的方法有待进一步改进。

针对上述风速预测方法中存在的不足，本文在粒子群优化算法的基础上，采用收缩因子对粒子速度更新的方式进行改进，加强粒子在寻优过程中的搜索能力，提出了采用改进PSO对LS-SVM参数寻优的方法，并建立基于改进PSO优化LS-SVM的短期风速预测模型，实例数据分析表明，基于改进PSO优化LS-SVM的风速预测方法在风速预测方面优于其他方法，验证了本文提出方法的正确性。

1 最小二乘支持向量机

最小二乘支持向量机(Least Squares Support Vector Machines，LS-SVM)是基于SVM的一种改进方法，它也遵循结构风险最小化原则，LS-SVM核函数的选择与SVM相同。二者的不同点在于，LS-SVM采用平方项作为优化指标，并将等式约束代替SVM的不等式约束[9]。

f(x)=w*φ(x)+b.

(1)

式中，φ(x)为非线性映射，w为权值向量，b为偏置量。

对于LS-SVM可将优化问题转化为：

(2)

式中，ξi为样本误差，C为惩罚因子，且C>0，其作用是对误差范围以外的样本数据进行调节。

此时，约束条件是：

yi[w·φ(xi)+b]=1-ξi, 其中i=1,2,…，l.

(3)

引入拉格朗日函数后可得：

(4)

式中，α为拉格朗日函数的乘子。根据KKT条件[10]得：

(5)

利用计算将w和ξi消去，得到如下方程组：

(6)

上式中：

(7)

令Ω=ZZT，带入核函数K(xi,xj)=φ(xi)T·φ(xj)，可得:

Ω=yiyjφ(xi)Tφ(xj)=yiyjK(xi,xj) .

(8)

故式(6)可写成如下形式：

(9)

利用最小二乘进行求解，即可得到LS-SVM的回归函数如下:

(10)

核函数的形式有多种，如线性、多项式和高斯径向基(RBF)等，在对样本进行回归分析时，通常采用高斯径向基核函数，RBF核函数的表达式如下:

(11)

式中，σ为核函数宽度，一般取常数。

2 改进粒子群优化算法

粒子群优化算法(Particle Swarm Optimization，PSO)是一种基于群体搜索的智能算法，它起源于飞鸟搜索食物，利用个体间保持竞争又相互合作的特点，在复杂的空间中找到最优解。因其具有简单，容易实现，并且没有较多的参数需要调节等优点，因此，经常被用于回归算法的参数寻优[11-12]。

假设D维空间存在种群X=(x1,x2,…,xN)，该种群包含N个粒子。把其中的第i个粒子看作是D维空间中的一个向量xi=(xi1,xi2,…,xil)T，即在D维空间中第i个粒子的位置。根据目标函数计算D维空间中各粒子位置xi的适应度值。第i个粒子速度的向量为Vi=(vi1,vi2,…,vil)T，个体极值的向量为Pi=(pi1,pi2,…,pil)T，群体极值的向量为Pg=(pg1,pg2,…,pgl)T。两个极值通过迭代更新粒子的速度和位置获得，即：

(12)

(13)

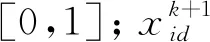
基本粒子群算法在搜索过程中过度依赖pbest和gbest，搜索能力有限，本文提出在PSO算法中引入收缩因子，收缩因子的变化既能保证PSO算法的收敛性，又能不受速度边界的影响，在加快种群的全局搜索速度的同时增强粒子的局部搜索能力。速度更新公式为：

(14)

(15)

式中，z为收缩因子，φ为总加速因子，gen为总迭代次数。K为收缩系数，用来控制PSO的全局和局部搜索能力，当它趋近1时，会造成大量的全局搜索行为，导致PSO算法收敛速度过慢；当它趋近0时，会造成大量的局部搜索，导致收敛速度过快。

仿真证明，在对多维函数进行优化时，引入收缩因子的粒子群算法在初始阶段拥有良好的全局搜索能力，而后期又能很好地进行局部寻优，其收敛性能良好，应用广泛。

3 改进PSO优化LS-SVM短期风速预测模型

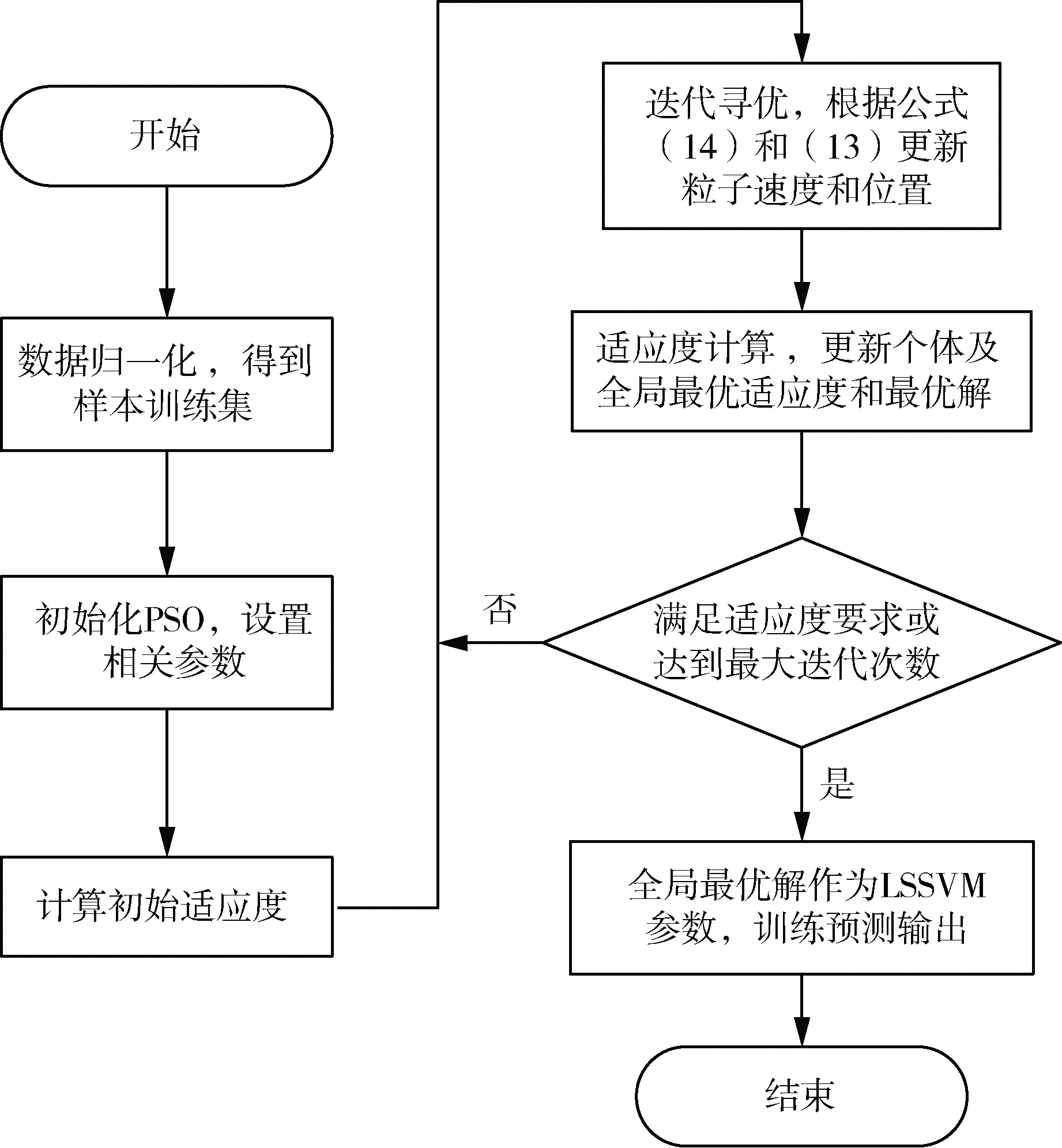
图1 预测流程图Fig.1 The flowchart of forecast

研究表明，LS-SVM算法非常适合小样本回归，具有较高的预测精度。但LS-SVM算法的预测效果受惩罚因子C和核函数参数σ的影响，当C和σ取值不当时，容易出现欠学习或者过学习的现象，均不利于样本回归。因此有必要采用寻优能力更强的改进粒子群算法，寻找LS-SVM算法的最佳参数组合。本文采用改进PSO优化LS-SVM算法的建模过程如图1所示。具体步骤如下：

(1)对风速样本进行预处理，样本数据由不同类别的数据组成，这些数据的单位均不相同，若直接建模，特征向量内积计算出的特征值太大不利于计算，本文采用公式(16)对样本数据进行归一化：

(16)

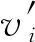
(2)初次训练LS-SVM，即初始化设置LS-SVM的核函数参数，令惩罚因子C=100，核函数宽度σ2=2.5，经预测模型运算后输出结果，然后根据下式计算适应度值。

(17)

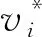
(3)初始化设置改进PSO参数，本文设置种群规模d=30，加速因子c1=c2=2.05，算法的总迭代次数gen=300，并采用线性递减的方法将惯性权重ω从0.9到0.4递减。

(4)把惩罚参数C和核函数参数σ作为粒子，初始值分别为C=100，σ2=2.5，将其记作当前个体最优解，并计算初始适应度值，搜索适应度值的最优解作为当前全局最优适应度值，与其对应的粒子即为全局最优解。

(5)迭代过程开始，根据式(13)和改进PSO公式(14)计算粒子新的速度及新的位置。

(6)将新的速度和位置作为核函数和惩罚因子重新带入LS-SVM算法进行训练输出，计算新适应度值。

(7)比较步骤(6)中的新适应度值和当前适应度值，如果新适应度值优于当前，则更新适应度值，并把新适应度值对应的粒子更新为个体最优值。

(8)如果新适应度值比全局适应度值更好，则更新为全局适应度值，并把与新适应度值相对应的速度和位置更新为全局最优解。

(9)判断迭代后的结果能否满足寻优及迭代次数的要求，若是则结束计算，输出全局最优解，若不满足则返回步骤(5)。

(10)将寻优后的核函数参数C和σ值带入LS-SVM风速预测模型，即可进行风速预测。

4 算例分析

引起风速变化的因素有很多，但主要因素为风向、温度和气压[13]。本文采用华北某风电场的在线监测装置中的数据进行仿真，监测装置距离风电场地面的高度为55 m，记录的时间间隔为10 min/次，记录的数据分别有风速、风向、气压和温度，在连续的时间序列上共选取100组数据用于仿真实验，依次编号为1到100，它们在时间序列上的变化如图2至图5所示。

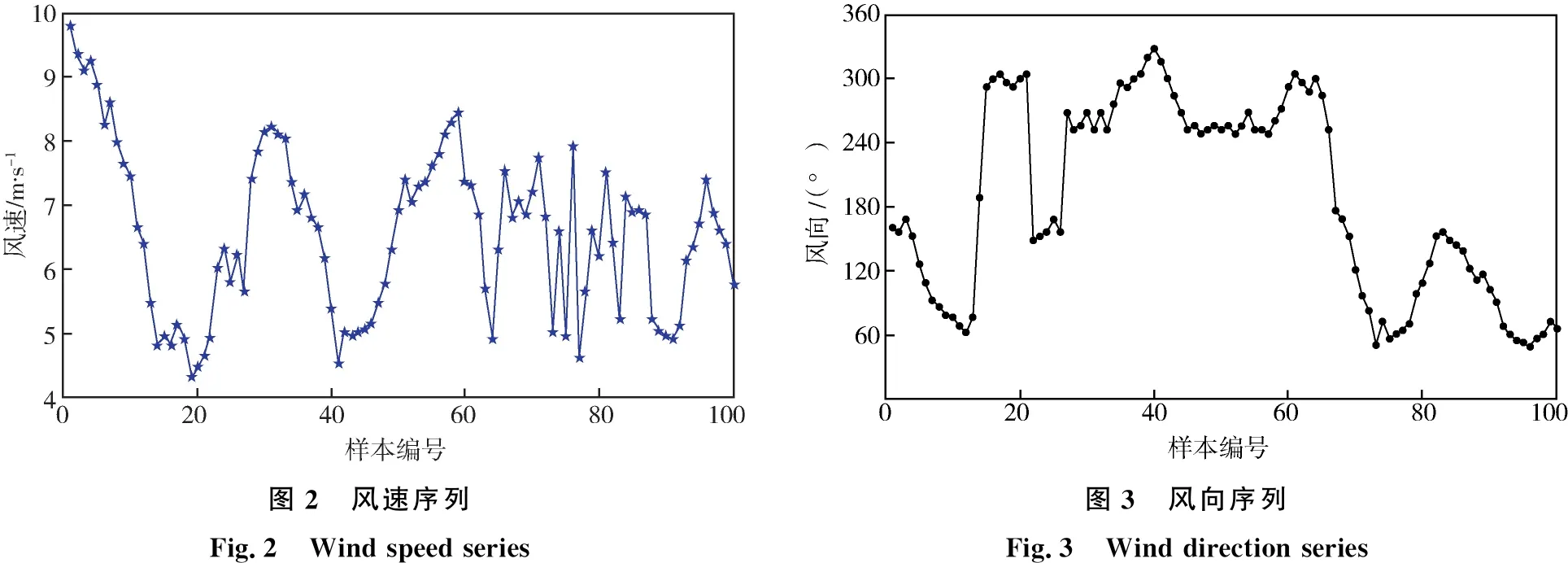
图2 风速序列Fig.2 Wind speed series图3 风向序列Fig.3 Wind direction series

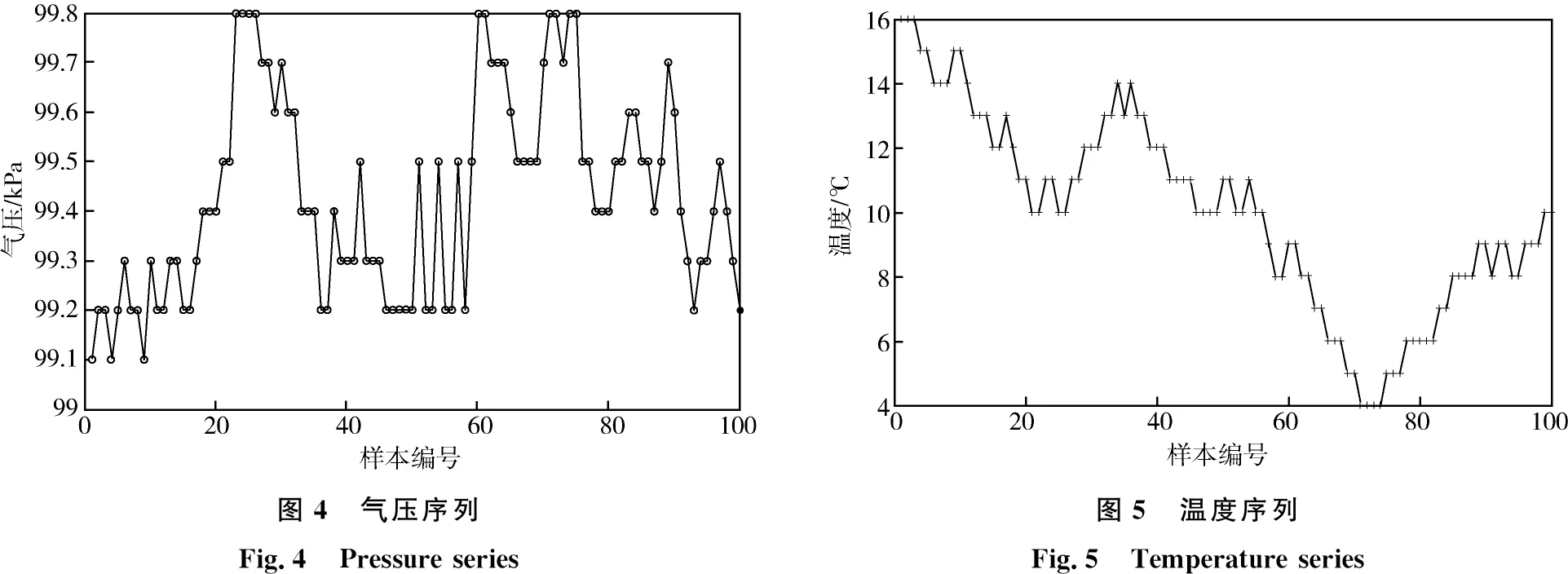
图4 气压序列Fig.4 Pressure series图5 温度序列Fig.5 Temperature series

为检验预测模型的精度，本文采用平均相对误差和均方根误差对本文提出的风速预测方法进行评价，平均相对误差和均方根误差计算公式如下:

(18)

(19)

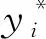
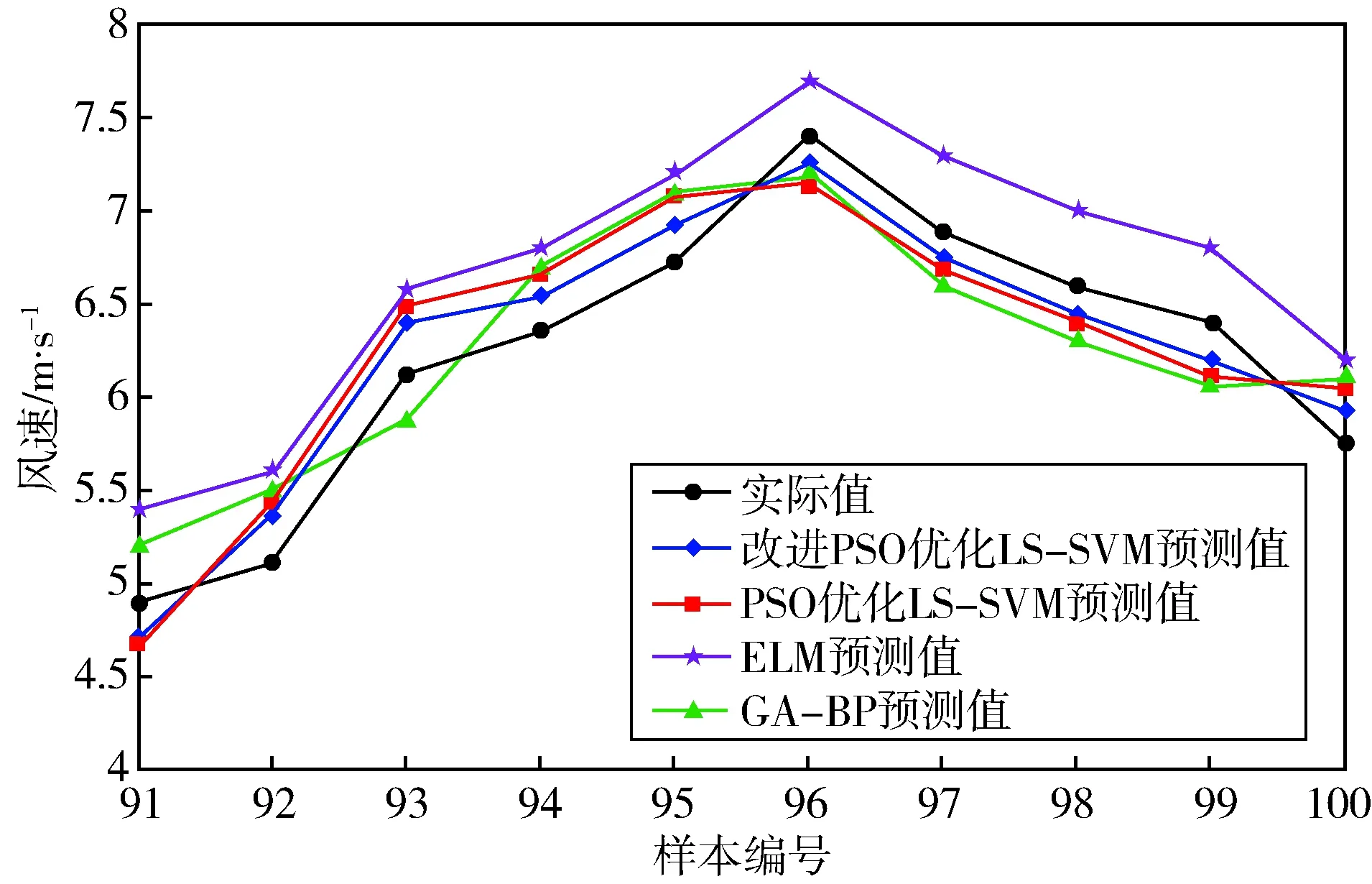
图6 测试集数据预测结果Fig.6 Prediction results of test set data

在MATLAB 2012b软件中进行仿真，本文把风向、气压和温度作为风速预测模型的支持向量，将100组样本数据分为两部分，前90组数据为训练集，后10组样本数据为测试集，采用训练集中的数据对预测模型进行训练，得出LS-SVM的最优参数组合为C=58.36和σ2=3.25，将最优参数赋给LS-SVM风速预测模型，对后10组测试集数据进行预测。采用相同数据建立PSO优化LS-SVM风速预测模型、ELM风速预测模型和GA-BP神经网络风速预测模型，四种风速预测模型的输出结果如图6所示。由图6可知，改进PSO优化LS-SVM风速预测模型的预测效果最好，ELM风速预测模型预测效果最差。

四种预测模型的平均相对误差和均方根误差如表1所示。由表1可知，改进PSO优化LS-SVM的风速预测模型的平均相对误差和均方根误差分别为3.72%和0.21，与其他模型相比均为最小，可见基于改进PSO优化LS-SVM的风速预测方法在风速预测方面优于其他方法，具有一定的应用价值。

表1 四种模型预测误差

5 结束语

(1)本文在粒子群优化算法的基础上，采用收缩因子对粒子速度更新的方式进行改进，保证粒子群算法在初始阶段拥有良好的全局搜索能力，而后期又能很好地进行局部寻优，提高算法的收敛性能，利用改进PSO对LS-SVM参数进行寻优，建立了基于改进PSO优化LS-SVM的短期风速预测模型。

(2)利用100组实际风速数据进行仿真，建立改进PSO优化LS-SVM风速预测模型、PSO优化LS-SVM风速预测模型、ELM风速预测模型和GA-BP神经网络风速预测模型进行对比分析，分析结果表明，改进PSO优化LS-SVM的风速预测模型的平均相对误差和均方根误差分别为3.72%和0.21，相较于其他模型，均为最小，验证了本文提出方法的正确性和实用性。