基于正交设计的糙条消能工评价方法

李凡琦，牧振伟，孙德旭，贾萍阳

(新疆农业大学水利与土木工程学院，新疆 乌鲁木齐 830052)

弯段溢洪道是水利工程中常见的溢洪道形态.水流进入弯道，由于受到离心力和边壁的顶托作用，在一个断面系统内形成封闭状态的横向环流，并在纵向水流的冲击下形成顺主流方向呈螺旋状的复杂水流.由于流动问题的复杂性和多元性，对于溢洪道弯段消能和导流方面的研究工作，一直是水利工程领域相当棘手的课题.

近年来，诸多学者主要是针对宽深比较小的(BH-1<2.5)溢洪道，在消能和导流方面进行了大量研究[1-3].现有的弯道消能导流措施多采用导流墩[4]、宽尾墩[5]、丁坝[6]和消力池[7-8]等，试图在设定的距离内调整弯道流态和控制横向环流的产生.

理论研究方面，罗索福斯基[9]借助量水管对弯道流速进行过系统测量，并推导出水面横比降和横向流速分布的计算公式；在此基础上，张红武等[10]、ODGAARD[11]分别对该公式进行了修正，其中，张红武公式与实际最为相符，且能反映底层环流较表层环流衰减更快的真实性.周建银等[12]采用量纲分析的方法，建立了考虑因素较传统理论公式更为全面的流速衰减长度经验公式；同期，周建银等[13]又在以往研究的基础上，针对弯道出流横向流速衰减公式忽略横比降的局限，推导出考虑横比降影响的横向流速发展的解析解.

研究方法方面，陈启刚等[14]通过全场无干扰的高频粒子图像测速仪(PIV)对高精度可变坡U型弯道三维时均流速场进行了多断面拍摄，为弯道流速的测量提供一种新的研究方法；同期，陈启钢等[15]将该法推广到明渠水流特征的研究中，并取得了良好的效果.

工程措施方面，白音包力皋等[16]以某电站进水管道为例，根据纵向流速分布沿横向的衰减与导流栅承担宽度(导流栅间距)增加一致的原理，并结合对弯道进口断面微元化处理的方法，导出了每个导流栅所承担的水流动量公式，为弯道导流方面的分析提供了一种新的方法.

在溢洪道消能和导流方面，国内外虽然进行了大量研究，以往的溢洪道弯段消能导流措施多适用于宽深比(溢洪道宽度与平均水深之比)较小的弯道，对于宽深比较大的弯段溢洪道消能导流问题研究较少，且在这方面理论知识匮乏、工程条件复杂.鉴于此，文中针对大宽深比(BH-1>5)的弯道消能和导流效果评价方法做研究.

1 试验概况

1.1 试验装置

试验模型由有机玻璃板拼接制成，分为模型主体、自循环供水系统和数据量测系统3个部分.模型主体分为进口直段、60°弯道段、出口调整段.模型断面形式全程采用矩形断面，其中进口直段长0.6 m，可充分保证水流在进入弯道前调整流速及水深.为了保证弯道水流的调整距离，出口调整段长1.40 m.弯道内外边壁由厚度3 mm的有机玻璃板热弯制成，可实现弯道转角的连续变化.溢洪道坡度系数i为0.025.试验过程中控制溢洪道宽度和下泄流量以改变宽深比，宽深比(B/H0)范围控制为5.20～14.50.试验模型具体结构示意及测点布置如图1所示.

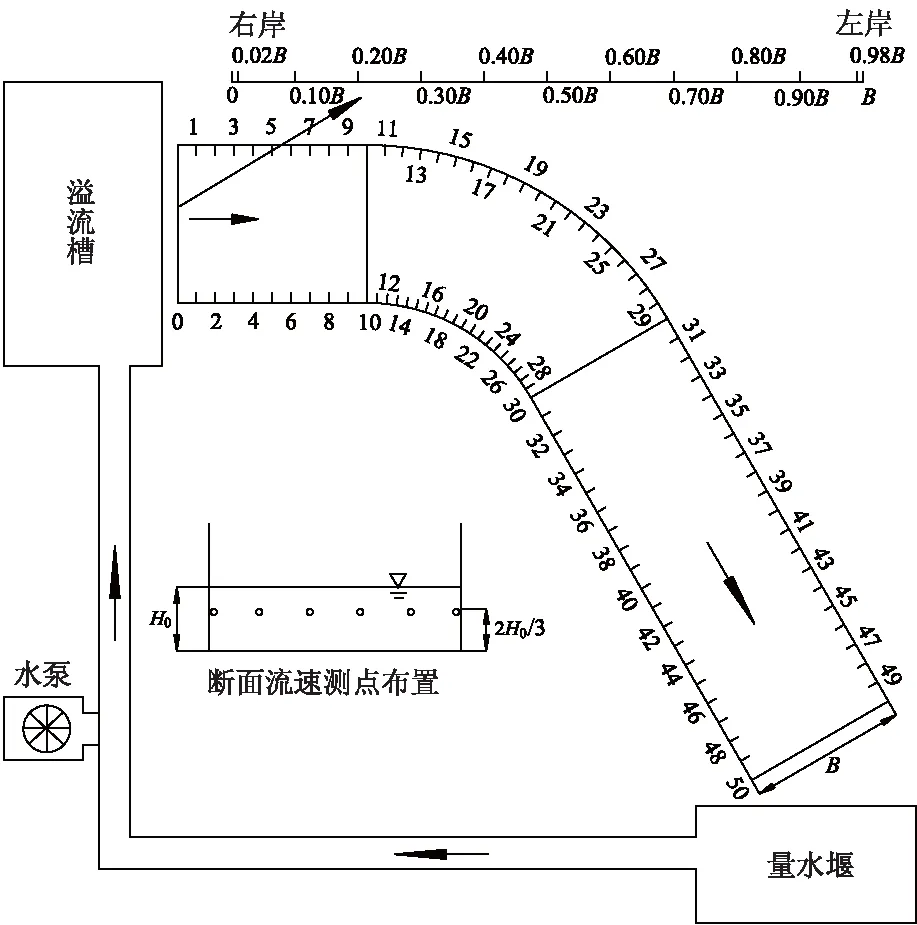
图1 试验模型具体结构示意及测点布置

糙条消能工主要布置在60°弯道段并紧贴床面，糙条中心沿弯道中轴线依次布置，糙条中心所在横断面与糙条之间的夹角θ分为18°，22°和26°，间距采用14，18，22 cm 3种布置形式；考虑到水流进入弯道后不均匀分布的因素，糙条布置高度h1-h2(h1为凹岸处糙条消能工的高度，h2为凸岸处糙条消能工的高度)分3种情况布置：凸岸为0.8，1.0，1.2 cm，对应凹岸高度为1.6，2.0，2.4 cm.糙条消能工布置结构及断面形式如图2所示.

图2 糙条消能工布置形式

1.2 试验测量

试验的下泄流量通过90°三角形薄壁堰进行测量，流量为

(1)

式中：H1为堰上水头高度；C0为三角形薄壁堰的流量系数.

(2)

式中：B为堰上游引水渠宽；P1为薄壁堰底板到堰角的距离.

通过测针对沿程断面水深依次测量.模型沿程选取51个测量断面，每个断面选取11个测点.测点0#和10#靠近边壁位置，分别选取距离边壁1 cm的位置作为测点，以减少边壁对测量结果的干扰.

由于溢洪道模型宽深比较大，沿程水深较浅，因此采用毕托管对时均流速进行测量.沿程共设置13个测流断面，每个断面均匀选取6个测点，测点位置为2H0/3处(H0为测点处的水深).靠近边壁处的测点同样选取距离边壁1 cm的位置进行测量.

2 建立评价指标

2.1 质量离散系数模型

为了更形象地反映糙条消能工对弯道段流速和水深的影响，提出了理想化断面质量分布模型.图3为其示意图，图中h(x)，v(x)分别为横断面x处的瞬时水深和瞬时纵向流速.将弯道横断面尽可能多地等分为x1，x2，x3，…，xn.

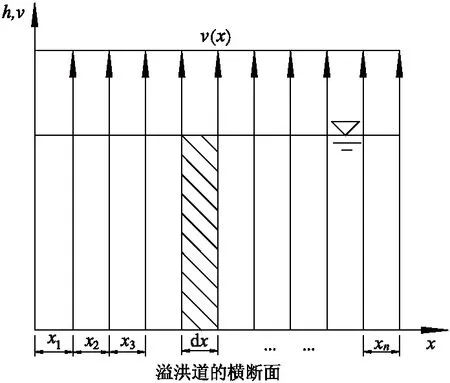
图3 弯道流体质量分布理想化模型示意图

理想状态下，假设糙条消能工的消能和导流作用使得横断面内各微元体所分布的水深和流速均相等，即

(3)

式中：ρ为流体密度；xi，xi-1为第i个微元体与第i-1个微元体之间的距离.

对公式(3)进行量纲分析，ρh(x)v(x)dx的量纲为[MT-1]，该等式表示单位时间通过微元体的质量.流体单位时间通过每个微元的质量用Mi表示，即

Mi=ρh(x)v(x)dx，

(4)

式中：Mi为第i个微元单位时间所分配的质量.

每个断面单位时间流体的质量离散程度用σ(标准差)反映，即

(5)

式中：σj为第j个断面质量分布的标准差.

为了方便对比分析各组试验之间的结果，正交试验结果分析应该考虑评价指标的整体性.将各断面瞬时质量分布的标准差进行叠加，并取其均值，得到能够反映整个弯道水深和流速分布情况的质量离散系数Cm，即

(6)

式中：j为初始断面标号；n为参加计算的断面个数.

质量离散系数Cm直接反映了断面水深和流速的离散情况，可以客观地对糙条消能工导流效果进行评价.

2.2 消能率

以弯道出口最低点处的水平面作为基准面.模型坡度系数为0.025.模型底面与水平面夹角较小，可以忽略坡度的影响.试验选取弯道的进口和出口断面为过水断面，过水断面上单位重量水体总机械能为

(7)

式中：E为过水断面上单位重量水体的总机械能；z0为位置水头高度；h为所取断面的平均水深；α为动能修正系数，取为1.0；v为断面平均流速；g为重力加速度.

消能率为

(8)

式中：η为消能率；E1，E2分别为上游和下游的过水断面上单位重量水体的总机械能.

3 正交试验设计

糙条消能工消能导流效果的影响因素众多，为了尽可能多地考虑各因素的影响，且减少试验数目，试验方案采用正交试验理论进行设计.选取糙条消能工的高度h1-h2、间距L、倾斜角度θ、弯道的曲率半径R、宽度B和下泄流量Q作为试验的因素，各因素分别用A′—F′表示，每个因素根据其自身特性分为3个水平.选取正交表L18(37)对试验进行设计，各参数的具体定量见表1.

表1 正交试验因素和水平

Tab.1 Factors and levels in orthogonal design of experiment

水平h1-h2/cmL/cmθ/(°)R/cmB/cmQ/(L·s-1)11.6-0.818181405020.022.0-1.024221706022.532.4-1.230262008025.0

评价弯道水流形态的水力要素众多，但在正交试验结果分析中，选取的评价指标应具有代表性和全面性.质量离散系数能够反映影响因素在导流方面的改善情况.消能率可以反映影响因素对水流的消能效果.因此，为了全面度量试验结果的优次，引入消能率和质量离散系数对试验结果进行评价.正交试验结果见表2.

表2 正交试验结果

4 结果分析

4.1 极差分析

采用极值分析法对试验结果进行分析.各水平试验结果的平均值Kxy为

(9)

式中：x为6种因素的集合，x∈{A′,B′,C′,D′,E′,F′}；y为水平数，y∈{1,2,3,}；Ixy为x因素第y水平的试验结果.

Ry表示Kxy的极差.Ry反映当各个因素的水平变动时，试验指标的变动幅度.也即Ry是反映6种因素的影响程度.Ry越大，说明对应因素的影响程度就越大；反之，Ry越小，说明对应因素的影响程度就越小.

表3为6种影响因素的极差分析结果.首先，使用Cm作为评价指标.从表中可以发现，流量对应的Ry最大，糙条消能工的间距对应的Ry最小.因此，就糙条消能工导流效果而言，流量的变化对试验结果影响最大.其次，使用η作为评价指标.在6种影响因素中，曲率半径对应的Ry最大，糙条消能工的间距对应的Ry最小.因此，曲率半径的变化对消能率影响最大.整体观察表3，糙条消能工的间距对2种评价指标的影响程度均是最低.

表3 影响因素极差分析

趋势图可直观地反映出试验指标随着水平变化而变化的规律，可以为下一步的试验指明方向.以各因素水平为横坐标，记作S；试验指标的平均值为纵坐标，记作T，绘制T-S趋势图，如图4所示.Cm的大小可以直接反映糙条消能工导流效果的优劣.Cm越趋近于1，则说明质量离散程度越小，也即弯道水深和流速分布越均匀；同样地，η越大，糙条消能工的消能效果越好.由图可知，以Cm为评价指标，可直观地看出最优参数组合为A′3B′2C′3D′2E′1F′3；通过η可得最优参数组合为A′3B′3C′1D′3E′3F′1.需要说明的是，上述参数组合并不是最佳组合，而是接近最佳组合.

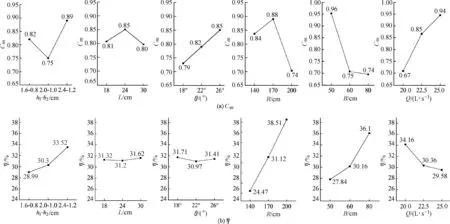
图4 T-S趋势图

4.2 相关性分析

影响糙条消能工消能导流效果的因素众多，各因素之间相互影响、相互制约.试验将糙条消能工的高度h、间距L和倾斜角度θ称为布置参数，将溢洪道的曲率半径Rf、宽度Bf和下泄流量Qf称为工程参数.为了找寻糙条消能工具有普适性的布置方法，定义量纲一因子Rd反映糙条消能工的综合特征，其表达式为

Rd=(ha/L)sinθ，

(10)

式中：ha为糙条消能工的平均高度，ha=(h1+h2)/2.

试验因素的相关性分析同样以Cm和η作为评价指标.图5为Rd与评价指标之间的对应关系，结果显示Cm和η均与Rd呈正比关系.Rd越大，Cm越趋近于1，也即糙条消能工的导流效果与Rd呈正向关系：Rd越大，糙条的导流效果越优.同样地，消能率也随着Rd增大而增大.但是，纯粹地研究Rd并不能全面地反映6种因素对评价指标的影响，Rd仅仅考虑了布置参数并没有考虑到工程参数的影响.因此，定义量纲一因子Rs反映工程参数的影响.Rs考虑了溢洪道的曲率半径Rf、宽度Bf和下泄流量Qf,同时考虑了黏性系数μ和弯道弯曲度Cu的影响.黏性系数μ的引入不仅考虑了边界条件(工程参数)，也考虑到了流体自身对导流效果的影响.

初步将各影响因素写成公式为

(11)

式中：Bf为溢洪道宽度；μ为运动学黏性系数，取为1.05×10-2Pa·s.

图5 Rd与评价指标之间的对应关系

弯曲度Cu是弧长与弦高之比，表示长条轧件(型、棒、管材)在长度方向上的弯曲程度.弯曲度囊括了弯道半径、转角等因素，能够更加客观地反映弯道特征，因此，采用弯曲度衡量溢洪道的弯曲特征显然也是合理的.弯道的弧长和弦高之间的关系如图6所示，Cu计算式为

(12)

式中：Rf为弯道曲率半径；β为弯道转角;l为弯道中轴线长.

图6 弯曲度计算示意图

式(11)可以写成

(13)

图7为Rs与评价指标之间的对应关系.对比图5a可以发现，Rs与Rd和Cm均存在正比例关系，但是Rs对Cm的影响明显大于Rd，就导流效果而言，工程参数的影响占主导地位；而且，随着Rs增大，Cm越趋近于1，也即消能工的导流效果与Rs呈正向关系.将图5b与图7b进行对比可以发现，Rd对η的影响较小，Rs对η的影响较大；随着Rs增大，η明显下降，这说明就消能方面而言，工程参数的影响仍然占主导地位.因此，在后续研究中，如果希望进一步提高糙条消能工的消能和导流效果，设计人员应从工程参数与布置参数两方面同时入手，找出两者之间的内在影响，方能真正地找寻两者之间的对应关系.限于篇幅，Rd与Rs之间的函数关系将另文探讨.

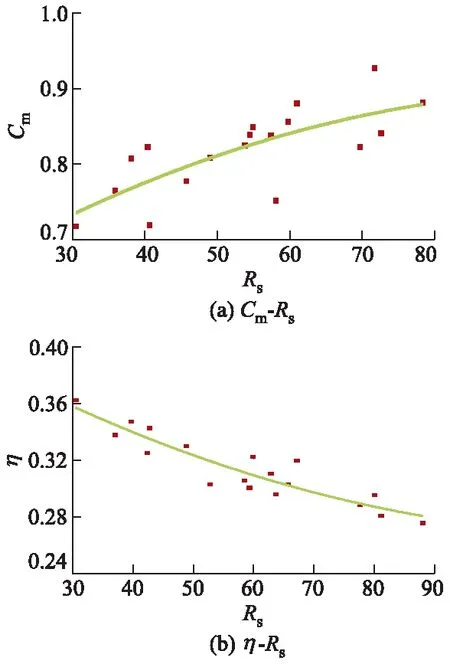
图7 Rs与评价指标之间的对应关系

5 结 论

采用正交设计的方法对宽深比较大的溢洪道布置糙条消能工进行模型试验.通过引入质量离散系数和消能率作为评价指标对试验结果进行分析.针对溢洪道消能和导流方面的研究工作，建立了一套系统的分析方法.通过上述结果分析，得到以下主要结论：

1) 评价指标可以直接反映糙条消能工的消能和导流效果.以Cm作为评价指标，各因素对Cm的影响程度从大到小依次是Q，B，h=R，θ，L，最优参数组合为A′3B′2C′3D′2E′1F′3.以η作为评价指标，各因素对η的影响程度从大到小依次是R，B，Q，h，θ，L，最优参数组合为A′3B′3C′1D′3E′3F′1.

2) 在整个弯段溢洪道水流形态研究中，布置参数Rd和工程参数Rs之间相互影响、相互制约.虽然从结果分析中观察到Rs对糙条消能工消能和导流效果的影响占主导地位，但是这并不能说明Rd对消能和导流效果的影响占次要地位，而只能说明对于不同的工程参数，都应有一个对应的最佳布置参数，使得Cm无限趋近于1.基于最佳Cm时Rd与Rs之间的函数关系仍需进一步研究.

3) 由于Mi具有真实的物理意义，因此，对于评价弯道导流措施的效果，Cm模型具有普遍的适用性.Rd和Rs均是量纲一参数，在找寻布置参数和工程参数之间的关系、推导糙条消能工布置公式方面，具有重要意义.