双蜗壳离心泵空化流动对隔舌处压力脉动特性的影响

杨敬江，李先军，潘中永，何松

(江苏大学国家水泵及系统工程技术研究中心,江苏 镇江 212013)

双蜗壳离心泵的结构特点是具有2个独立且对称布置的蜗壳流道，可以减小由于单蜗壳内不对称流动产生的径向力[1]，在大型离心泵中得到了广泛应用.谈明高等[2]通过数值模拟分析了双蜗壳泵在不同时刻泵内结构变形的特点.张帆等[3]通过数值计算发现双蜗壳离心泵压力脉动主要产生于叶轮出口和蜗壳进口的交界面位置，且主要脉动频率为叶频及其倍频.上述研究主要分析了双蜗壳结构对泵的性能和内部流动的影响，而较少关注双蜗壳离心泵空化流动对压力脉动的影响情况.

目前对于离心泵空化的研究主要有试验和数值模拟2种方法.FRIEDRICHS等[4]采用可视化手段得到了空泡的分布特点和空泡在叶轮内部的演变过程. SINGHAL等[5]建立完全空化数学模型，并通过试验验证其可准确模拟空泡的演变过程.刘厚林等[6]研究了不同空化模型在离心泵空化流动中的适用性.王松林等[7]利用数值模拟研究离心泵内空化流动和压力脉动特点，结果表明叶轮内压力脉动主频为叶轮转频.张德胜等[8]研究了轴流泵叶轮内空泡分布状态.高波等[9]研究了离心泵空化流动的非定常激励特点，探究了压力脉动强度和空化流动发展的关系.LEE等[10]研究了空化流动对叶轮所受径向力的影响.袁建平等[11]研究了离心泵回流旋涡的空化特点，发现在小流量工况下泵内发生回流空化且具有低频特性. LIU等[12]研究了混流泵的压力脉动与叶顶间隙泄漏涡之间的关系.

文中以一台双蜗壳离心泵为研究对象，采用SSTk-ω湍流模型和Zwart-Gerber-Belamri空化模型，对设计工况下的泵内空化流动和无空化流动进行非定常数值模拟，预测设计工况下泵内空化发生的位置和发展状态，研究空化流动诱导隔舌部位压力脉动的变化，旨在研究双蜗壳结构对空化流动的影响，为双蜗壳泵内空化状态监测和预防提供理论依据，给空化流动诱导泵振动噪声机理相关研究提供新的参考.

1 计算模型

选取的双蜗壳离心泵的最高效率点性能参数分别为流量Qd=185.4 m3/h，扬程Hd=82.5 m，转速n=2 950 r/min，比转数ns=89.2.泵的主要几何参数分别为叶轮进口直径D1=160 mm，轮毂直径dh=60 mm，叶轮出口宽度b2=16 mm，叶片数Z=5，隔舌安放角φ0=25°，排出口直径Dd=100 mm，双蜗壳的隔板位置见图1.图2为采用UG软件对泵水体进行三维造型.

图1 蜗壳平面图

图2 三维造型

2 数值计算

2.1 网格划分

对泵进行全流道数值计算，包括泵进口段、叶轮、蜗壳及泵出口段，叶轮和双蜗壳结构复杂，采用适应性好的非结构网格，并且在蜗壳的隔舌处进行了网格加密.表1为3组不同数量N的网格无关性验证，表中Ht,Hc分别为扬程的试验值和计算值.选用网格2为计算网格，各部件的网格质量在0.35以上，且叶轮部分的y+值为36，符合数值计算要求，主要部件网格划分结果如图3所示，最终确定计算域网格总数为2 548 957.

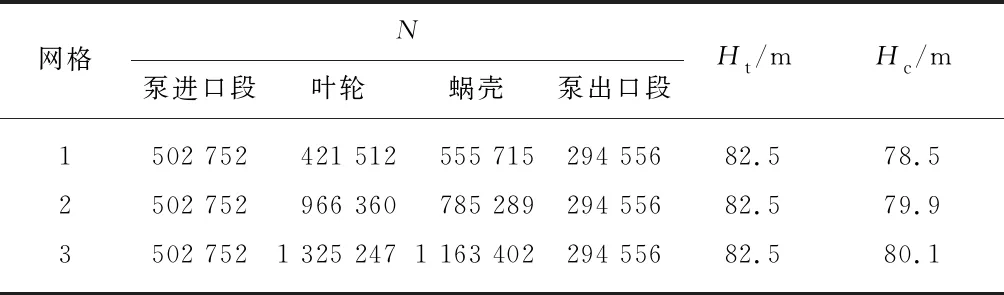
表1 网格无关性验证

图3 计算网格

2.2 控制方程

离心泵内空化流动可以看成一种均匀气液混合物流动，采用基于均质多相传输模型的连续性方程和动量方程来描述空化流动.

(1)

(2)

ρm=ρlαl+ρvαv,

(3)

式中:ρ为密度；α为体积分数；ui,uj为速度分量；p为压强；δij为克罗内克数；μ,μt分别为混合物的动力黏度和湍流黏度；下标m,l和v分别为混合相、液相和气相.

湍流模型选用在水力机械空化流计算中较为理想的SSTk-ω模型.

2.3 空化模型

空化模型采用ANSYS-CFX软件中集成的基于Rayleigh-Plesset方程的Zwart-Gerber-Belamri空化模型，其气相控制方程为

(4)

R=Re-Rc,

(5)

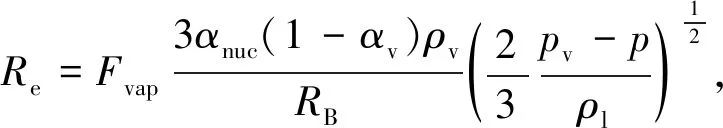
(6)

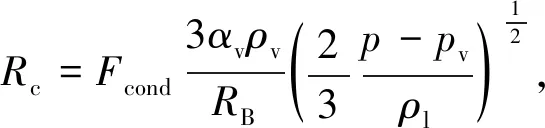
(7)

式中:αv为气相体积分数；R为相间质量传输率；ρv为气相密度；ui为气相速度；Re为蒸气生成率；Rv为蒸气凝结率；Fvap为蒸发经验系数,Fvap=50；Fcond为凝结经验系数,Fcond=0.01；αnuc为成核位置体积分数；RB为空泡半径;p为流场压力；pv为介质在工作温度下的饱和蒸气压.

2.4 边界条件和时间步长设置

流体域的进口为压力进口，出口为质量流量出口，壁面设为绝热无滑移壁面，在进行空化计算时，进口处的液相和气相的体积分数分别为1和0.计算时间步长为叶轮旋转2°所需时间，为1.13×10-4s，计算总时长为叶轮旋转10周所需时间，为0.203 s.

3 计算结果分析

3.1 外特性分析

如图4所示，设计工况下，扬程和效率的计算值与试验值误差分别为3.2%和2.0%，非设计工况下的计算值与试验值基本一致，且计算值略低于试验值，最大误差不超过5.0%，表明选用的计算模型能满足要求.

图4 泵水力性能曲线

3.2 空化模拟分析

泵的有效空化余量NPSHA的计算公式为

(8)

式中:pin为泵进口压力；pva为流体在工作温度下的饱和蒸气压；vs为泵进口的流体速度；ρ,g分别为流体密度和重力加速度.

根据泵的有效空化余量的计算公式和模拟结果绘制成预测空化性能曲线，如图5所示.

图5 设计工况下泵空化性能预测曲线

泵扬程下降3%时所对应的装置空化余量为临界空化余量NPSHC,根据数值模拟结果,计算出在设计工况下的临界空化余量为NPSHC=4.05 m.

图6为泵在设计工况点不同空化余量下，叶轮内部的空泡体积分布.由图6可以看出：随着装置空化余量降低，叶轮内部发生空化的程度加剧，尤其是当装置空化余量降低到临界空化余量以下时，叶轮内部出现大规模空化状态，叶片吸力面产生大量空泡，进而导致叶片吸力面被空泡覆盖，堵塞流道，严重削弱叶片做功能力，导致扬程急剧降低；泵内空化的空泡初始产生于叶轮叶片进口吸力面根部，随着空化余量的降低，空泡云沿着叶片吸力面向叶片出口和前盖板方向发展，叶轮内部空泡的发展并不均匀，加剧了叶轮内部流动的不稳定性.

图6 不同空化余量下空泡分布图

3.3 空化压力脉动特性

为了准确描述双蜗壳离心泵的空化流动对隔舌处的压力脉动影响，在隔舌A和B处各设置了3个相邻间隔5°的压力脉动监测点，分别为P1,P2,P3,P4,P5和P6，如图7所示.

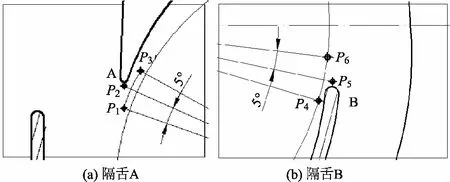
图7 压力脉动监测点设置

采用压力系数Cp分析压力脉动特点，即

(9)

图8为设计工况时，在空化和无空化流动状态下，叶轮旋转1周的压力脉动时域信号图，可以看出：隔舌A处的监测点P1，P2和P3的压力脉动具有明显的周期性特点，监测点P1在空化与无空化流动状态下的压力脉动规律一致，表明该处的流动受泵内空化影响较小；受到隔舌位置附近紊乱的流动影响，监测点P2在空化与无空化流动状态下的压力脉动规律有明显差异，压力脉动幅值受空化流动影响较大，空化流动状态下的压力脉动峰值是无空化流动状态压力脉动峰值的2倍；在无空化流动状态下，监测点P3与监测点P1的压力脉动变化规律基本一致，而在蜗壳断面与隔舌的共同作用下，监测点P3的压力脉动受到空化流动的影响，但在空化流动状态下的压力脉动峰值变化不大；隔舌B处的监测点P4，P5和P6的压力脉动同样具有周期性的特点；监测点P4和P5在空化与无空化流动状态下的压力脉动变化规律一致，空化流动对监测点P4的压力脉动影响较小，而监测点P5的压力脉动受空化流动影响较大，且该处空化流动状态下的压力脉动峰值是无空化流动状态下压力脉动峰值的2倍；监测点P6位于隔板进口的上游位置，流动状态受隔板影响较小，在空化与无空化流动状态下的压力脉动规律与监测点P4和P5差异较大，监测点P6在空化流动状态与无空化流动状态下的压力脉动变化一致，表明该处受空化流动的影响较小.

图8 隔舌A和B不同监测点的压力脉动时域图

图9为相应的压力脉动频域图，可以看出，在设计工况点，泵内发生空化和无空化状态下，监测点P1，P2，P3，P4和P6处的压力脉动主频均为245.8 Hz，为叶轮叶片通过频率，而点P5在空化状态下压力脉动主频为叶频，在无空化状态下压力脉动主频为2倍叶频.

图9 隔舌A和B不同监测点的压力脉动频域图

4 结 论

1) 在设计工况下，双蜗壳离心泵内发生空化时，空泡初始产生于叶轮叶片进口吸力面根部.随着装置空化余量的降低，空泡云沿着叶轮叶片吸力面向叶片出口和前盖板方向发展.叶轮内部空泡的发展并不均匀，叶轮内部不稳定流动加剧，导致泵振动产生噪声.

2) 在空化状态下，双蜗壳离心泵隔舌A，B处的压力脉动均呈现出周期性，不同监测点的主频均为叶频，且在靠近隔舌位置的点P2，P5的压力脉动幅值有显著增长，其峰值均为对应无空化状态下压力脉动峰值的2倍.