基于改进Hodrick-Prescott分解模型的近红外自适应降噪方法
2020-05-25谢德红李俊锋万晓霞
谢德红,李俊锋,刘 菂,万晓霞,叶 艺
1. 南京林业大学轻工与食品学院,江苏 南京 210037 2. 河南牧业经济学院包装与印刷工程学院,河南 郑州 450046 3. 北京工商大学食品安全大数据技术北京市重点实验室,北京 100048 4. 武汉大学湖北省文物颜色信息数字化与虚拟再现工程研究中心,湖北 武汉 430079
引 言
农药的高效防治功能,对促进农作物增产、缓解农产品供需矛盾有举足轻重的作用。然而,农药大量不合理使用,导致农药残留超过食品安全标准,引发诸多食品安全问题[1]。当前一些化学、生物等检测方法精度虽高,但存在耗时费力、破损被测物、污染环境等缺点,难以满足现代农业快速、无损、批量及实时检测的需求。近红外光谱因其无损、快速、无污染的特点,在农药残留定性和定量检测应用中优势明显。但是,近红外光谱是典型的弱信号,被测物化学组分的谱峰相对微弱且重叠度高。此外,由于近红外光谱采集仪器和采集环境等因素,实测近红外光谱常受噪声干扰。在后续近红外光谱数据分类中,无法有效区别此光谱中被测物化学组分信息和噪声,进而影响分类精度。有效地去除光谱数据中的噪声,对建立稳定性好、分类精度高的农药残留检测的分类模型十分重要。
小波分解[2-3]和经验模太分解(empirical mode decomposition, EMD)[4-5]可较好刻画光谱信号的特征,近些年常被用于近红外等各类光谱信号的降噪中,并在信噪比小时有一定抑制噪声的效果。小波分解方法是在小波分解的基础上通过阈值手段去除噪声,因此小波分解的基函数(即小波基)和阈值选择与染噪光谱特征的适应性对降噪至关重要。有研究[3]提出利用Stein无偏风险估计(Stein’s unbiased estimate of risk, SURE)有效地解决了阈值自适应问题,但小波基与染噪光谱特征的匹配问题却鲜有研究关注。据文献[6]研究发现,当小波基与被分解信号特征不匹配时,重构信号易产生Gibbs震荡现象。此震荡波破坏了光谱的几何特征,导致在后续近红外光谱数据分类中易被误认为被测物化学组分的谱峰,恶化分类精度、影响微弱的农药残留成分的正确分析。EMD克服了小波基与被分解信号相适应的要求,可将任意特征的光谱信号分解成不同的震荡成分,即本征模态函数(intrinsic mode functions, IMFs),但在信号重构时易产生混叠模态问题。混叠模态是由经验模分解的过程中信号因局部极值在很短的时间(或很短的波段)间隔内发生多次跳变导致的。在光谱信号染噪后,混叠模态中的信号状态很难完全避免。为此,有学者提出了集合模态分解(ensemble empirical mode decomposition,EEMD)[4]。此方法是一种噪声协助分析方法,因而当分解出的IMFs数量比较有限时,各IMFs不可避免的存在噪声,导致重构信号的信噪比降低。互补集合模态分解(complete ensemble empirical mode decomposition, CEEMD)[5]可抑制IMFs里的残余噪声,但当参数选择不当时,会产生错误成分使最后获得的IMFs不能真正满足IMFs的定义,导致重构信号仍会存在一些小震荡,在近红外光谱中呈现为额外的谱峰。为了提高近红外光谱的信噪比、减少光谱信号的失真以及额外谱峰的产生或残留、满足果蔬农药残留定性检测的应用需求,本研究提出了L曲线与Hodrick-Prescott分解模型相结合的自适应降噪方法,复原被测物表面原始近红外光谱,为后续近红外光谱数据分类、农药残留检测、及农药残留化学组分信息分析和挖掘奠定基础。
1 改进Hodrick-Prescott降噪的原理与方法
Hodrick-Prescott分解模型[7]是一种信号分离方法,广泛用于经济数据中经济趋势和各时间点震荡波的分离。在果蔬农药残留的近红外光谱中,用以表征被测物化学组分的谱峰相对较弱且时常发生重叠,因而其光谱波形随波长的变化相对缓慢,如同经济趋势的特征; 通常,近红外光谱采集过程中所产生的噪声随波长变化相对剧烈,如同经济数据中随时间点变化的震荡波特征。因此将依据染噪近红外光谱的特征,建立基于Hodrick-Prescott分解模型的近红外光谱降噪的方法,并与bior6.8小波分解方法、sym8小波分解方法、互补集合模态分解方法进行比较,验证本方法的有效性。
1.1 Hodrick-Prescott降噪原理与方法
设被测物的原始近红外光谱(即未染噪声的近红外光谱)为f=(fi,…,fj)∈Rn,其近红外光谱在采集过程中受广义高斯噪声的污染获得染噪近红外光谱为s=(si,…,sj)T∈Rn,它们与噪声e=(ei,…,ej)T∈Rn,关系如下
s=f+e
(1)
下标i和j表示波长,n为近红外波长范围内的波长点的数量。
利用Hodrick-Prescott分解方法降噪是通过引入一定约束条件,将光谱信号复原为具有存在性、唯一性且适定的结果,且此结果为受噪声干扰小的过程。已知染噪近红外光谱信号s,求原始近红外光谱f的Hodrick-Prescott分解方法可转化为目标函数J(f)的最小化问题
J(f)=(1/2)‖s-f‖2+κ‖Df‖2
(2)
此目标函数由残差项和正则化项两部分构成。其中,‖s-f‖2为残差项,保证复原信号的保真度; ‖Df‖2为正则化项,约束近红外光谱f的波形特征;D(n-2)×n为二阶差分矩阵

(3)
用于惩罚复原光谱信号的震荡波动,迫使其趋向梯度减少的方向。‖·‖2表示l2范数。κ≥0为正则化参数,用以调整目标函数两部分的权重。若κ=0,正则化项的惩罚作用失效,求得的复原光谱信号f趋于染噪光谱信号; 反之,若κ→+∞, 则正则化项惩罚起主导作用,求得的复原光谱信号f只会尽可能满足‖Df‖2最小,因而其复原光谱信号逼真程度比较差、偏离原始光谱信号,甚至无法呈现原始光谱信号的基本波形。由此可知,选择合适的正则化参数κ,对获得最优降噪效果至关重要。
1.2 正则化参数自适应获取方法
依上所析,正则化参数κ越大、惩罚越严重,复原出的光谱信号越平滑、含震荡波动程度越弱。虽易去除噪声,但也存在平滑掉有利于数据分类的小谱峰的危险; 反之,正则化参数κ越小,正则化项的惩罚作用越小,复原光谱信号则越易残留噪声。此外,原始Hodrick-Prescott方法中的正则化参数κ的选择是非自适应的,选择一个固定值,难以适应实测近红外光谱非稳定特征及实测近红外光谱信噪比有大有小的状况。基于此,为了使正则化参数与实测染噪近红外光谱能自适应,提出利用L-曲线方法[8]获得Hodrick-Prescott方法中的自适应值。
L-曲线是指各正则化参数下对应复原光谱信号的残差项‖s-fκ‖2与正则化项‖Df‖2所构成的log-log尺度曲线,其形状接近L形。
l:={(log‖s-fκ‖2, log‖Dfκ‖2):κ≥0}
(4)
其中,“l”表示L-曲线,fκ为每个κ值下的复原光谱信号。由式可知,每个κ值均存在一个最优fκ使目标函数J(f)趋于最小。由此,L-曲线上每个点则表示每个κ值下的最小J(f)值,其拐点表示所有最小J(f)值中最小值,且拐点处对应的κ值则为与当前染噪光谱信号最优适应值。
2 结果与讨论
实验采集341个上海青(一种青菜)近红外光谱样本,并在采集的近红外光谱上人工添加广义高斯噪声作为降噪对象。为验证本方法的有效性,选用bior6.8和sym8小波基的SURE阈值方法[3]及CEEMD方法[5]作对比,并采用信噪比(signal noise ratios, SNR)、均方根误差(root mean square error, RMSE)及降噪光谱数据训练所得分类模型识别率评价降噪效果。
2.1 实验数据
以无锡迅杰光远科技有限公司的IAS-2000近红外光谱仪为近红外光谱采集设备,光谱仪采集参数设置如下: 平均采样次数为30次,采集波段为900~1 700 nm,测量间隔为1 nm。光谱采集环境: 装有空调的恒温环境(23 ℃)内。采集的实验样品为无农药残留上海青和喷洒了乐果(农药,C5H12NO3PS2)的上海青。其中,无农药残留上海青购自农贸市场,并通过小苏打和食盐浸泡、自来冲、蒸馏水先后冲洗晾干; 残留农药上海青则由无农药残留上海青喷晒不同浓度配比的乐果溶液并晾干所得。其中,乐果为河南省周口市德贝尔生物化学品工程有限生产的40%乐果乳油; 不同浓度配比的乐果溶液由蒸馏水稀释所得,且稀释的最小和最大倍数分别为50倍和1 500倍。实验分别采集残留农药样本291个、未残留农药样本50个。从农药残留样本和未残留农药样本中分别选取146个农药残留样本和25个未残留农药样本构成训练样本集,剩余为测试样本集。其中,146个农药残留样本上的乐果浓度横跨最小与最大配比。
为了便于验证降噪效果,设定上述采集的近红外吸收光谱为原始纯光谱信号,模拟叠加不同程度高斯噪声后的光谱为实验待处理的染噪光谱。图1上排图为稀释50倍的农药残留样本,叠加噪声后的近红外光谱信噪比分别为19.07 dB[如图1(a)]和18.79 dB[如图1(b)]。

图1 染噪近红外光谱和其L-曲线(a): SNR=19.07 dB; (b): SNR=18.79 dBFig.1 Noise-contaminated NIR spectroscopy and their L-curve(a): SNR=19.07 dB; (b): SNR=18.79 dB
2.2 降噪效果与分析
对任一组染噪近红外光谱,可利用L-曲线方法获得此光谱的自适应κ值,其步骤执行如下: 先设定κ的范围和步长,设定κ=0.001, 0.002, …, 29.999, 30; 然后分别计算各κ值下残差项‖s-fκ‖2与正则化项‖Df‖2的值,在获得L-曲线的基础上,获取曲线最大曲率点处的κ值; 最后,在此κ值下,利用Hodrick-Prescott方法复原的近红外光谱fκ即为降噪后的近红外光谱。依上述步骤,图1中两组染噪近红外光谱的自适应正则化参数分别为0.91和0.11,如图1(a,b)下排图所示。
为了衡量、比较降噪效果,首先采用了SNR和RMSE两个指标。其中,SNR值大小与降噪效果成正比,RMSE值大小则与降噪效果成反比。表1利用SNR和RMSE两个指标比较了bior6.8和sym8小波的SURE阈值方法(均为五层小波分解)[3]、CEEMD方法[5]、以及本方法。首先,通过SNR和RMSE值的横向比较发现,本方法的SNR值最大、RMSE值最小,说明相对其他三种方法,本方法的降噪效果最优。其次,结合两组染噪近红外光谱的纵向数据比较发现,降噪方法优劣顺序未随噪声不同而变化,说明本文方法对不同噪声的降噪效果相对稳定。SNR和RMSE均是从全局的角度考察降噪前后光谱相似程度,未能反映局部缺陷,而局部缺陷恰恰容易恶化后续数据的分类精度。例如,当降噪后光谱出现沿未染噪光谱上下波动的小波峰波谷,且波峰和波谷构成的增加和减少的面积能相互抵消时,SNR和RMSE则不能从数据上体现额外小波峰波谷的局部缺陷存在,但此额外产生的小波峰波谷在后续数据分类中又极易误认为是物质化学组分的谱峰,影响分类的精确度。因此,本研究将继续从局部和后续数据分类精度进一步验证降噪效果。
当被测物含量有限时,其近红外光谱(或其对应化学组分的近红外光谱谱峰)也比较弱。例如,在本实验中,上海青本身的化学组分含量一般远高于残留农药的化学组分,因而农药残留上海青的近红外光谱中除较弱的、反映农药化学组分的谱峰外,主要为宽波段特征、且信号较强的上海青化学组分的近红外光谱。此特点使得残留样本的近红外光谱与未残留样本的近红外光谱识别度小。为了增强农药谱峰的可识别度,在近红外光谱数据分类、判断农药残留与否的过程中,常用导数处理方式抑制背景光谱信号(如上海青的近红外光谱)、增强目标识别物化学组分的谱峰(如农药化学组分的谱峰)。一阶导数的处理方式是双刃剑,会增强农药化学组分谱峰也会放大噪声等非光谱成份,但均有利于从局部判断降噪后光谱与原未染噪光谱的相似度。因此,利用光谱一阶导数谱图进一步评判各方法的降噪效果,如图2所示。
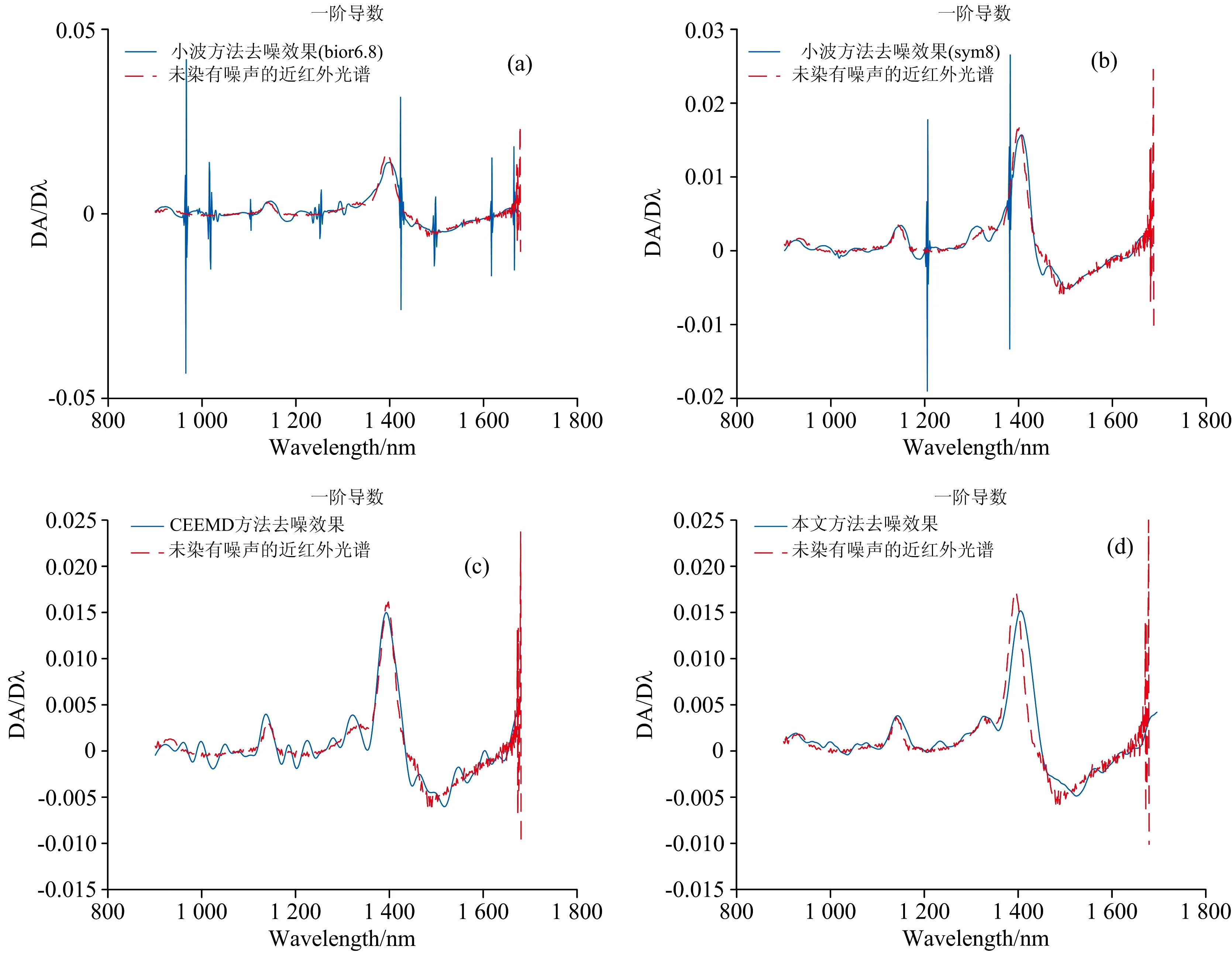
图2 降噪后光谱和未染噪声光谱的一阶导数谱图(a): 小波法(bior6.8小波核); (b): 小波法(sym8); (c): CEEMD法; (d): 本方法Fig.2 First derivative spectrum of the denoised NIR spectroscopy and its original(a): Wavelet method (with bior6.8 wavelet kernel); (b): Wavelet method (with sym8 wavelet kernel);(c): CEEMD method; (d): The proposed method
图2各分图均为图1(a)对应染噪近红外光谱经过降噪和一阶求导后的结果。图中实线代表降噪后光谱的一阶求导结果,虚线则代表原未染噪声光谱的一阶求导结果。在图2(a)中,实线图谱大约于980,1 020,1 100,1 290,1 410,1 500和1 620 nm等波段处呈现明显的震荡波,而此震荡波在虚线的谱图上均不可见。由此推测,此额外震荡波为bior6.8小波方法降噪所产生、非被测物化学组分,会干扰后续光谱数据的分类、恶化分类精度; 图2(b)显示sym8小波方法也会产生较强的震荡波; 图2(c)实线图谱中虽无明显的震荡波,但相对于虚线所示谱图,仍然呈现额外的小波峰波谷,此小波峰波谷与某些物质化学组分的近红外二级和三级倍频波[9]难以区分,也极易被误当作上海青或农药的化学组分的小谱峰; 图2(d)中实线与虚线表示的谱图比较接近,且无明显额外的震荡波和小谱峰。由此分析可知,从局部特征判断,相对上述其他三种降噪方法,本方法降噪后的效果优,也更有益于后续化学组分分析以及农药残留检测为目的的数据分类。
表1 降噪前后近红外光谱信噪比与均方根误差对比
Table 1 Comparison of signal-to-noise ratio and the root mean square error of the denoised NIR spectroscopy

染噪光谱SNR评价指标sym8bior6.8CEEMD本方法19.07SNR32.6332.5633.0735.75RMSE0.011 70.011 80.011 10.008 218.79SNR31.6931.5031.7133.35RMSE0.013 00.013 30.013 00.010 8

表2 降噪前后近红外数据的SVM分类结果Table 2 SVM classification results baseddifferent denoising methods
研究近红外光谱降噪的主要目的是减少噪声对后续农药残留检测中数据分类的干扰,从而提高训练所得分类模型的拟合能力和泛化能力。由此,对染噪训练样本数据和测试样本数据降噪处理后,再经过一阶导数预处理、主成分分析(PCA)选取十维特征的前提下,建立检测农药残留与否的支持向量机(SVM)[10]分类模型,并分别通过训练样本数据和测试样本数据获得此分类模型的识别率,以进一步评价降噪方法优劣。表2比较了原未染噪光谱及四种方法降噪后光谱的分类效果。由分类原理可知,上述额外震荡波和小谱峰的存在,会导致分类数据在特征空间的分布结构发生变化,不仅影响训练所得分类模型拟合数据的能力,更会恶化分类模型的泛化能力(即正确识别非训练近红外光谱数据所属类别的能力)。表2中的数据显示了与理论推导一致的结论。由表2中的分类模型的识别率还可发现,本方法降噪后的光谱数据训练所得的SVM分类模型,其训练集和测试集的识别率远高于其他三种方法的结果,接近原始无噪声近红外光谱数据的结果。此结果表明,本方法降噪效果优良,且对分类模型的准确率影响最优。
3 结 论
提出了一种改进Hodrick-Prescott分解模型的自适应近红外光谱降噪方法,充分利用Hodrick-Prescott分解模型中正则化项对复原光谱的惩罚作用,迫使复原光谱倾向于梯度减少的方向,并结合L-曲线方法自适应地获取了Hodrick-Prescott分解模型中正则化参数,从而实现了染噪近红外光谱自适应降噪的目的。实验从信噪比、均方根误差及分类模型识别率数据证明了本降噪方法具有一定的优越性,可为近红外光谱定性检测提供可靠的噪声预处理方法。
