激光焊接等离子体光谱辐射传输模型
2020-05-25朱日宏
王 念,沈 华*,朱日宏
1. 南京理工大学电子工程与光电技术学院, 江苏 南京 210094 2. 南京理工大学先进固体激光工业和信息化部重点实验室,江苏 南京 210094
引 言
近年来,激光焊接以其形变小、熔深大、效率高的优点[1],已经逐步取代传统焊接技术,在造船、车辆制造、航空航天等领域得到广泛应用[2-5],激光焊接工艺的好坏,对这些行业的发展有着重要的影响。激光焊接过程往往伴随着光致等离子体的产生,了解等离子体在多个波长下的光谱辐射场三维分布,能够帮助研究人员获取等离子体的温度场分布、电子密度场分布以及其他一些物理量的三维分布,对于改进激光焊接工艺具有重要的意义。
当利用CCD等探测器从某个方向对等离子体进行探测时,其靶面上所接收到的光谱辐射强度,是沿着其观测方向上等离子体辐射的累积效应。通过探测器各像素上的积分值去反演观测路径上的辐射强度变化,以得到整个等离子体光谱辐射场的三维分布是研究人员着重研究的方向,该问题可归结为由投影重建图像的问题。要解决这一问题,首先要弄清楚等离子体的辐射传输过程,掌握辐射叠加到探测器表面这一物理过程,并进行相应的建模。目前常用的辐射传输模型有平行投影模型与中心投影模型。平行投影模型[6]是基于医学CT应用场合下的模型,其光源为平行光源,探测器各像素所获得的光谱辐射来自于平行于光轴的投影线上的等离子体各发光点,且各像素的投影线互相平行。然而在利用CCD进行探测时,在光学镜头的成像作用下,对各像素表面的辐射产生贡献的发光点不再是平行于光轴的投影线上的发光点,此时利用平行投影模型就会产生较大的误差。上海交通大学孙大为等[7-8]在前者的基础上,提出了更为准确的中心投影模型。该模型将CCD镜头看作针孔,以针孔为中心,以像素与针孔的连接线作为投影线,认为对像素灰度产生贡献的是该投影线上的各等离子体发光点。该模型采用针孔模型作为CCD镜头的成像模型,在镜头口径较小时是适用的。然而在实际应用时,若要满足更高的光谱辐射场反演的空间分辨率要求,则要采用较大的镜头口径,此时针孔模型与实际的成像模型之间存在较大的差异,这将导致辐射传输模型精度下降,并最终影响激光焊接三维光谱辐射场的重建。针对以上模型存在的缺陷,本文基于辐射度量学与光学成像的原理,针对大口径观测设备的需求提出了一种新的等离子体光谱辐射传输模型,为提高激光焊接等离子体光谱辐射场的反演精度奠定模型基础。
1 光谱辐射传输模型
若将等离子体离散的划分为j=m×n×l个正方体的网格,则各网格的光谱辐射叠加到CCD靶面上某一像素的过程可表示为式(1)
(1)
式(1)中,Pi为像素i所接收到的光谱辐射值;ωi, m, n, l为辐射比例系数,其定义为像素i所接收到来自网格(m,n,l)的辐射通量占其总辐射通量的比例,f(m,n,l)表示网格(m,n,l)的光谱辐射通量。若遍历CCD靶面各像素对应的光谱辐射接收过程,则式(1)可用矩阵表示为
I=WX
(2)
式(2)中,I表示二维投影,即CCD靶面各像素所接收到的光谱辐射通量值;W是辐射比例系数矩阵,由辐射比例系数ωi, m, n, l组成;X代表各等离子体网格的待重建光谱辐射值。
本文所建辐射传输模型,即是要将W准确的表达出来: 将网格(m,n,l)被探测器镜头所接收到的光谱辐射通量占其向周围空间发出的总光谱辐射通量的比例定义为辐射比例系数ω1,将网格(m,n,l)被像素i所接收到的光谱辐射通量占其被探测器接收到的光谱辐射通量的比例定义为辐射比例系数ω2。各网格的光谱辐射比例系数ω可由两个部分相乘所得,即ω=ω1ω2。
1.1 辐射传递模型ω1的建立
将等离子体中的任一点看作点光源,以球面波的形式向外发出辐射。CCD所接收到的辐射通量占点光源所发出的总辐射通量的比例ω1,应为被CCD镜头占据的球冠所对应的立体角与整个球面立体角之比,即该部分球冠覆盖的球面面积Sg与整个辐射球面面积S之比。
1.1.1 轴上点模型
当点光源位于光轴上时,镜头所占据的是正上方的球冠,即整球冠。设透镜半径为R,点光源与镜头表面之间的轴向距离为L,辐射球面半径为r,则位于探测器镜头轴上等离子体任一点的比例系数ω1为
(3)
1.1.2 轴外点模型
对于等离子体中那些位于光轴之外的点而言,其占据的是部分球冠。则位于探测器镜头轴外等离子体任一点的比例系数ω1的表达式为
(4)

1.2 光学成像模型ω2的建立
等离子体被划分为网格后,各网格经CCD镜头成像,于靶面上形成光斑,其发出的辐射能量均匀的分布在光斑上。网格(m,n,l)的辐射比例系数ω2,应为网格在CCD靶面上的光斑与像素i的重叠面积SC和光斑总面积SB之比。利用CCD观察等离子体时,由于网格边长远小于网格与镜头之间的轴向距离,因此可以将网格看作一个没有厚度的正方形薄片来代替其成像情况。
1.2.1 网格在最佳物面上的成像模型
设镜头焦距为f′,CCD靶面到镜头的距离为L′。当网格(m,n,l)位于距离镜头L的最佳物面(即靶面关于镜头的共轭物面)上时,在靶面上所形成的光斑为薄片经镜头所成的像。如图1所示,光斑的位置以及轮廓,可由薄片的四个顶点的像点A′,B′,C′和D′确定。设CCD靶面与最佳物面之间的垂轴放大率为β,由高斯公式和垂轴放大率公式,可得A′,B′,C′和D′的坐标,以及光斑的面积
(5)

(6)
因此,当网格位于最佳物面时,其辐射比例系数ω2的表达式为
(7)
1.2.2 网格不在最佳物面上的成像模型

(8)
此时网格在CCD靶面上所形成的光斑轮廓如图2(b)所示: 由正方形A′B′C′D′轮廓上各点以其弥散斑向外拓展所得。由光斑面积SB、光斑与像素i的重叠面积SC,可得当网格(m,n,l)不在最佳物面时,辐射比例系数ω2的表达式为
(9)

图1 等离子体中位于最佳物面上的网格成像示意图Fig.1 Imaging of cubes on the optimum surface

图2 光斑与像素重叠情况示意图(a): 网格位于最佳物面上时; (b): 网格不在最佳物面上时Fig.2 Overlapping of spot and pixel(a): When the cube is on the optimum surface;(b): The cube is not on the optimum surface
2 仿真实验
将等离子体辐射场尺寸设定为Lx×Ly×Lz=6 mm×6 mm×6 mm,划分为30×30×30个网格。为模拟真实辐射场分布,将等离子体温度设定在1 000~3 000 ℃之间。根据普朗克辐射定律,利用发射率函数基形式不变法[9],由各网格的表面积计算其光谱辐射通量,得到等离子体在波长为λ1=400 nm,λ2=500 nm,λ3=600 nm、λ4=700 nm的设定光谱辐射场。分别在等离子体正上、正面、侧面距离120 mm处放置CCD,镜头焦距为50 mm,通光口径D为100 mm。根据辐射度量学原理,模拟CCD靶面探测到的光谱辐射分布。利用不同的辐射传输模型计算辐射比例系数,由式(2)建立各自的方程组,通过代数重建法[10](algebra reconstruction technique, ART)反解,重建光谱辐射场分布,重建误差采用均方根误差,即
(10)
式(10)中:X为等离子体辐射场设定值,X*为反演值。
2.1 对称场
设定对称等离子体辐射场的温度分布表达式为
(11)
式(11)中,h为距离工件表面的长度,x和y为以焊接激光光轴为z轴下的平面直角坐标。分别利用本文所提模型、中心投影模型重建等离子体光谱辐射通量分布场,并与原设定场比较,结果如表1所示。由表1可以看出,利用本文模型进行重建的相对误差在8%以下,中心投影模型的相对误差在9%左右。说明在对称场下,本文模型具有较好的重建精确度。本文模型反演所得到的400 nm波长下的光谱辐射场,在某一截面的分布与设定场的分布对比,如图3所示。由图3可见反演分布与设定分布呈现很好的一致性。

表1 单峰对称等离子体辐射场重建精度对比Tabel 1 Comparison of reconstruction accuracy of single-peak symmetrical radiation field
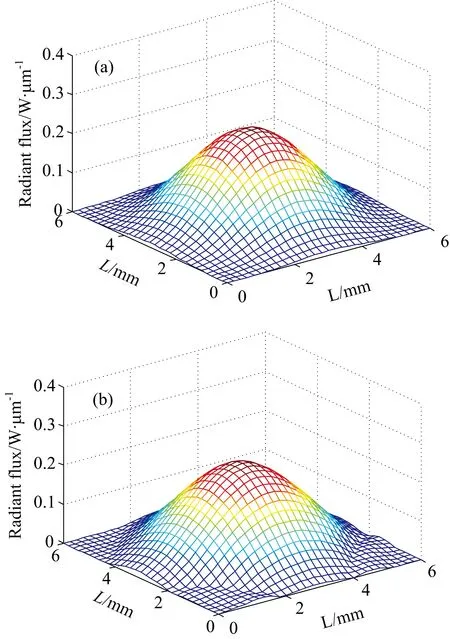
图3 本文模型反演结果与对称设定场对比(λ1=400 nm)(a): 设定辐射场; (b): 反演结果
Fig.3 Comparison between the reconstruction result with the model presented in this paper and the set symmetrical radiation field (λ1=400 nm)
(a): The set field; (b): The reconstruction result
2.2 非对称场
设定非对称等离子体辐射场的温度分布表达式为
(12)
式(12)中,x1=0.6,y1=0.6;x2=0.6,y2=-0.6;x3=-0.6,y3=0.6;x4=-0.6,y4=-0.6。等离子体某一截面上的温度分布如图4所示。
分别利用本文模型、中心投影模型重建光谱辐射场,结果如表2所示。由表2可以看出,本文模型重建相对误差在11%以下,中心投影模型在27%左右。说明在非对称场下,本文模型具有较好的重建精确度。本文模型反演所得到的400 nm波长光谱辐射场,在某一截面与设定场对比,如图5所示。由图5可见二者呈现很好的一致性。

图4 非对称辐射场某一截面的温度分布Fig.4 Temperature distribution of a section of a asymmetrical radiation field

表2 四峰非对称等离子体辐射场重建精度对比Tabel 2 Comparison of reconstruction accuracy of four-peak asymmetrical radiation field

图5 本文模型反演结果与非对称设定场对比(λ1=400 nm)(a): 设定辐射场; (b): 反演结果
Fig.5 Comparison between the reconstruction result with the model presented in this paper and the set asymmetrical radiation field (λ1=400 nm)
(a): The set field; (b): The reconstruction result
3 结 论
针对激光焊接等离子体光谱辐射场重建领域大口径观测设备的需求,分别基于辐射度量学与光学成像原理,对光谱辐射从等离子体发出到被观测镜头收集的过程与辐射进入镜头后到达探测器靶面的过程进行研究,提出了一种基于光学成像的光谱辐射传输模型。与现有模型相比,该模型具有较好的反演精度,能够为精确的解算激光焊接等离子体辐射场提供模型基础。
