求解伪单调型变分不等式的一种投影算法

陈 园， 何诣然

（四川师范大学 数学科学学院，四川 成都610066）

设F 是Rn→Rn的一个连续映射，C 为Rn 的一非空闭凸子集.本文考虑经典的Hartman -Stampacchia变分不等式问题：求x*∈C使得

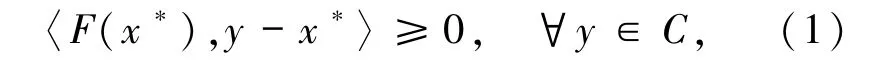
其中〈·，·〉是欧几里德内积.

变分不等式在经济、交通等领域中有着广泛的应用.关于用数值迭代法求解变分不等式的研究，已有着丰富的成果［1-12］.投影算法是求解单调型变分不等式的主要算法，削弱变分不等式单调性假设条件是研究变分不等式的重要内容.文献［3］中的算法3.2 及文献［11］中第72 页的算法，为叙述简便将其分别记为算法1 和2，具有以下的迭代形式：

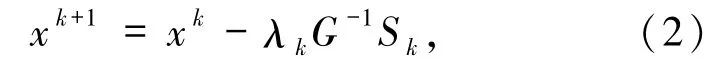
其中λk是严格大于0 的步长，G 是一对称正定矩阵，Sk是第k次迭代步选取的迭代方向.近年来，关于（2）式的算法研究可参见文献［13 -19］.为使算法简洁，将对称正定矩阵G取为单位矩阵.

算法1 在每一步迭代中，通过Armijo 线性搜索

确定τk，令

其中τk＝αnkτk-1，nk是满足（3）式成立的最小非负整数，α∈（0，1），τ -1∈（0，∞），

ΠC（x）表示x到闭凸集C上的投影，θ∈（0，2），δ∈（0，1）.该算法在F 为单调连续映射且（1）式有解的条件下是全局收敛的.

算法2 在每一迭代步中，使用（3）式的Armijo线性搜索，并令

其中

该算法在F 为单调连续映射且（1）式的解集非空的条件下是全局收敛的.

注意到算法2 的迭代步，由

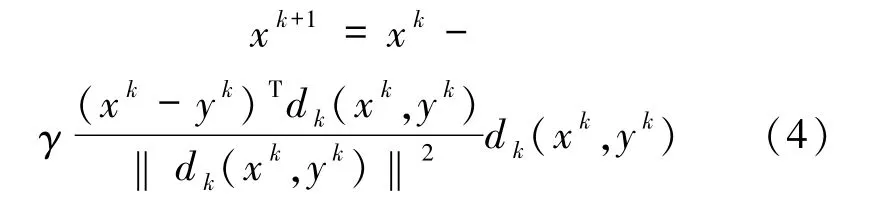
易得，xk+1恰为xk在超平面

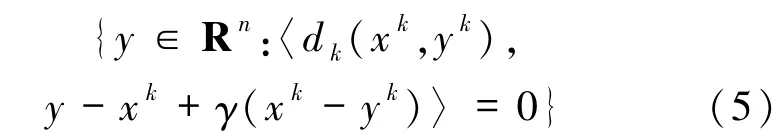
上的投影.本文令γ∈（0，1］，τk：＝αnk，α∈（0，1），通过（5）式中的超平面，证明了当变分不等式（1）的解集非空且F 为伪单调连续映射时，所提算法3.1 是全局收敛的，其中nk是满足（3）式成立的最小非负整数.

近20 年来，已有较多的文献研究了用投影型算法求解伪单调型变分不等式问题，如文献［4 -9］.为后文叙述方便，对任意一个正实数μ，任意x∈Rn，记rμ（x）＝x -ΠC（x -μF（x））.文献［4 -9］中共使用了2 种与（3）式不同的Armijo 线性搜索.文献［4，6，8］中使用了Armijo线性搜索

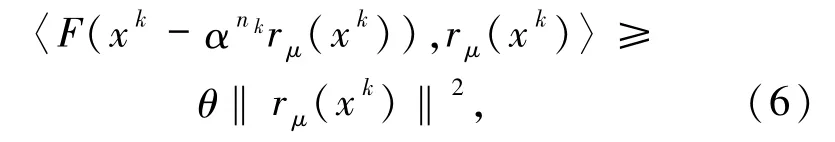
而文献［5，7，9］中使用的Armijo线性搜索为

其中α∈（0，1），θ与μ均为正数且取值相关，nk是满足不等式（6）或（7）成立的最小非负整数.易得，在每次迭代中Armijo线性搜索（6）与（7）式较之于（3）式，计算投影算子的次数更少，事实上使用（3）式，每一次nk取值的变动将计算一次投影算子.本文中使用的Armijo 线搜索与（6）和（7）式虽不同，但可以将文献［4 -9］及本文中的算法获得下一迭代步xk+1的步骤统一为如下形式：

其中Hk为某超平面或半空间，αk为第k 步的步长，dk为第k步的迭代方向.则文献［4，7 -9］中的算法对任意非负整数k，αk＝0，文献［4，8］的

文献［7，9］中的算法4 的

文献［6］中算法对任意非负整数k，Hk为全空间Rn，

且需满足

文献［5］中算法NVE-2 的

而本文算法在生成下一迭代步xk+1时，对任意非负整数k，

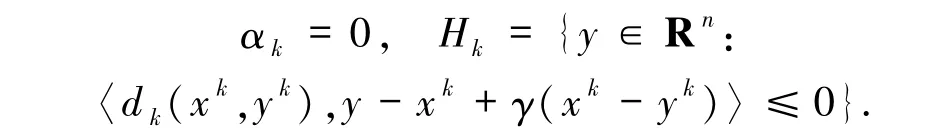
文献［10］的算法1 使用了与（3）、（6）和（7）式形式均不同的Armijo线性搜索

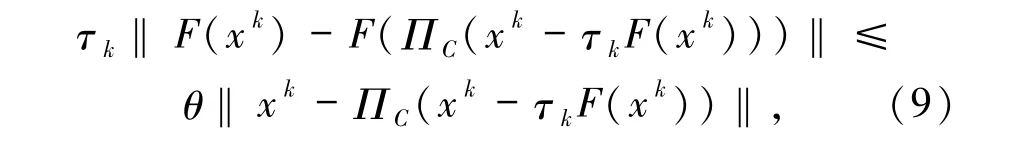
且生成下一迭代步xk+1的等式形如（2）式，该算法的

其中

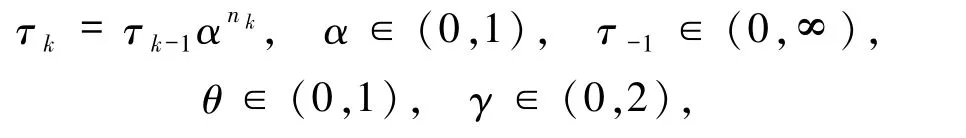
nk是使（9）式成立的最小非负整数.易知（9）式的Armijo线性搜索较之于（6）和（7）式，在每次迭代中仍可能计算更多次的投影算子.本文引理2.1 的证明中指出了它与Armijo 线性搜索（3）式的关系，该算法在F 为伪单调连续映射且（1）式的解集非空的条件下，全局收敛.

为书写简洁，将文献［7］的算法1. 1 与文献［10］的算法1，分别记为算法3 和4.虽然本文算法2.1 中的Armijo线性搜索较之于（6）和（7）式，在每次迭代中可能计算更多次的投影算子，但不失为一种新的投影型算法，且本文关于例3.1 的数值计算结果可说明，在求解某些变分不等式问题时，本文算法2.1 比算法1 ～4 收敛得更快.记问题（1）的解集为S，本文始终假定S≠Ø，F为伪单调连续映射.

3 数值实验

本节给出数值实验，在Windows 10，处理器为Intel（R）Core（TM）i5 -3317UCPU＠1.70GHz的系统环境下，使用版本为R2015b，优化工具为toolbox 7.3 的MATLAB 进行数值实验.在计算过程中，允许误差为ε ＝10-8，即当‖r1（xk）‖2≤10-8程序终止.令算法2.1 中参数取为：τ0＝1，δ ＝0.2，α ＝0.5，γ ＝0.8，并将其与算法1 ～4 比较，其中算法1的参数取值为τ -1＝1，θ ＝1.5，δ ＝0.1，α ＝0.3；算法2 的参数取值为γ ＝1.5，α ＝0.5，δ ＝0.2，τ -1＝1；算法3 中参数的取值为α ＝0.5，θ ＝4，μ ＝0.2；算法4 中G取单位矩阵，α -1＝1，α ＝0.5，γ ＝1.5，θ ＝0.5.令x0代表初始点，nf表示计算f的次数，i表示程序迭代的次数，t代表程序运行所需的时间，x 表示最后一个迭代点.

例3.1 令C ＝［10，20］，F（x）＝x3，则F（x）在C上是单调映射，易得10 是该变分不等式问题的解，将算法2.1 与算法1 ～4 进行比较，得到的数值结果如表1 ～4 所示.

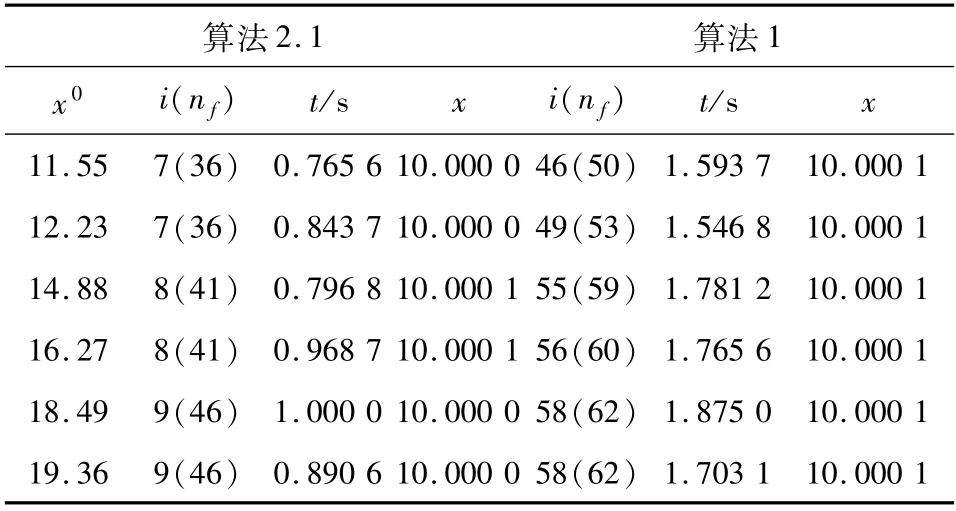
表1 例3.1 的数值结果Tab. 1 Numerical results of example 3.1

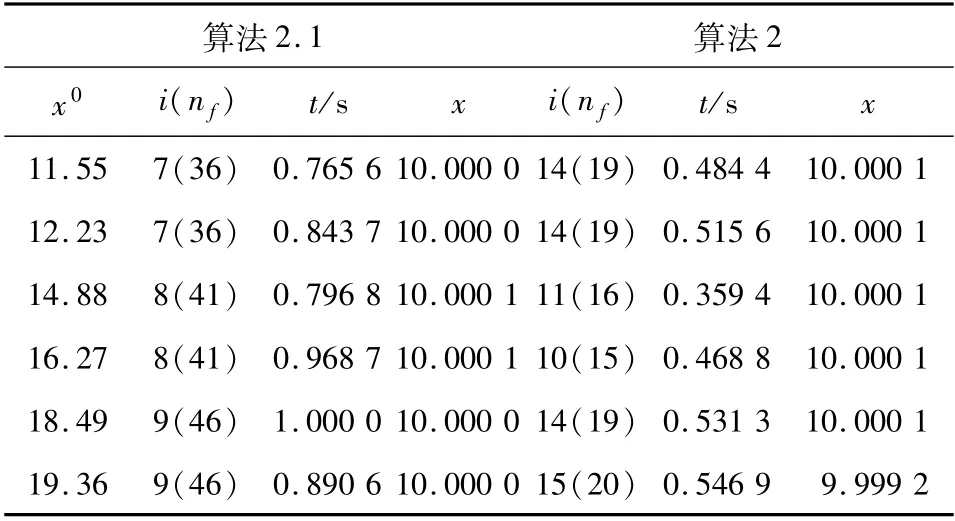
表2 例3.1 的数值结果Tab. 2 Numerical results of example 3.1

表3 例3.1 的数值结果Tab. 3 Numerical results of example 3.1

表4 例3.1 的数值结果Tab. 4 Numerical results of example 3.1

4 结论

本文算法2.1 可用于求解伪单调型变分不等式.在例3.1 中，较之于算法1 ～4，算法2.1 有更好的收敛效果.能否进一步削弱变分不等式的条件及探索算法2.1 的更多应用，是将来进一步的工作.