带磁场项的非线性Schrödinger 方程解的有限时间爆破

帅 鲲， 潘志刚， 蒲志林， 熊 胤

（1.电子科技大学 成都学院，四川 成都611731； 2.西南交通大学 数学学院，四川 成都610031；3.四川师范大学 数学科学学院，四川 成都610066； 4.四川师范大学 法学院，四川 成都610066）

本文考虑如下带磁场项的非线性Schrödinger方程：

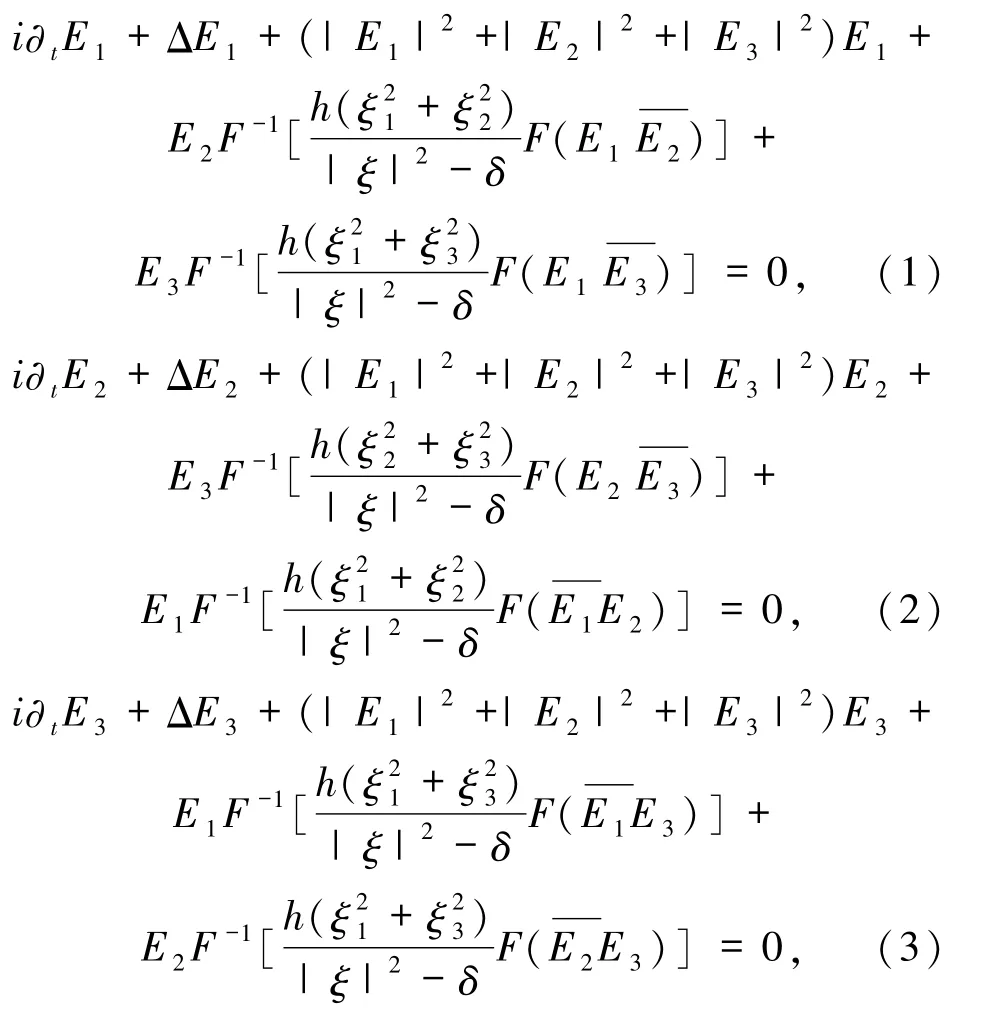
其初值满足：

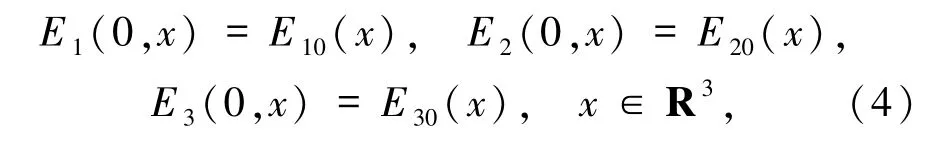
其中，E（t，x）为R+×R3到C3的矢量函数，常数δ≤0，h ＞0.方程（1）～（3）也称为带奇异积分算子的非线性Schrödinger方程.

若不考虑磁场项的影响，方程（1）～（3）简化为

其中E ＝（E1，E2，E3）.该方程为量子力学中的经典模型.目前，关于不带磁场项的Schrödinger 方程的解爆破性质的研究已经比较成熟［1-2］.然而，对带磁场项的Schrödinger 方程（1）～（3），尽管物理学上已经表明了解在有限时间爆破［3-4］，据我们所知还没有方程（1）～（3）奇异解存在的结果.

基于文献［5 -8］的方法，克服非线性奇异积分算子的困难，得到了方程（1）～（4）柯西问题在有限时间爆破的初值条件.

1 预备知识

令wi＞0，Ei（t，x）＝eiwitui（x），i ＝1，2，3，（u1（x），u2（x），u3（x））为以下静态问题的解：

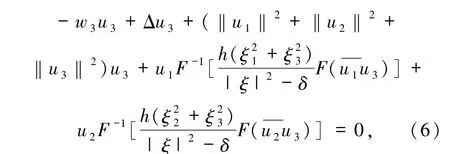
其中（u1，u2，u3）∈H1（R3）×H1（R3）×H1（R3），（u1，u2，u3）≠（0，0，0）.定义以下泛函：

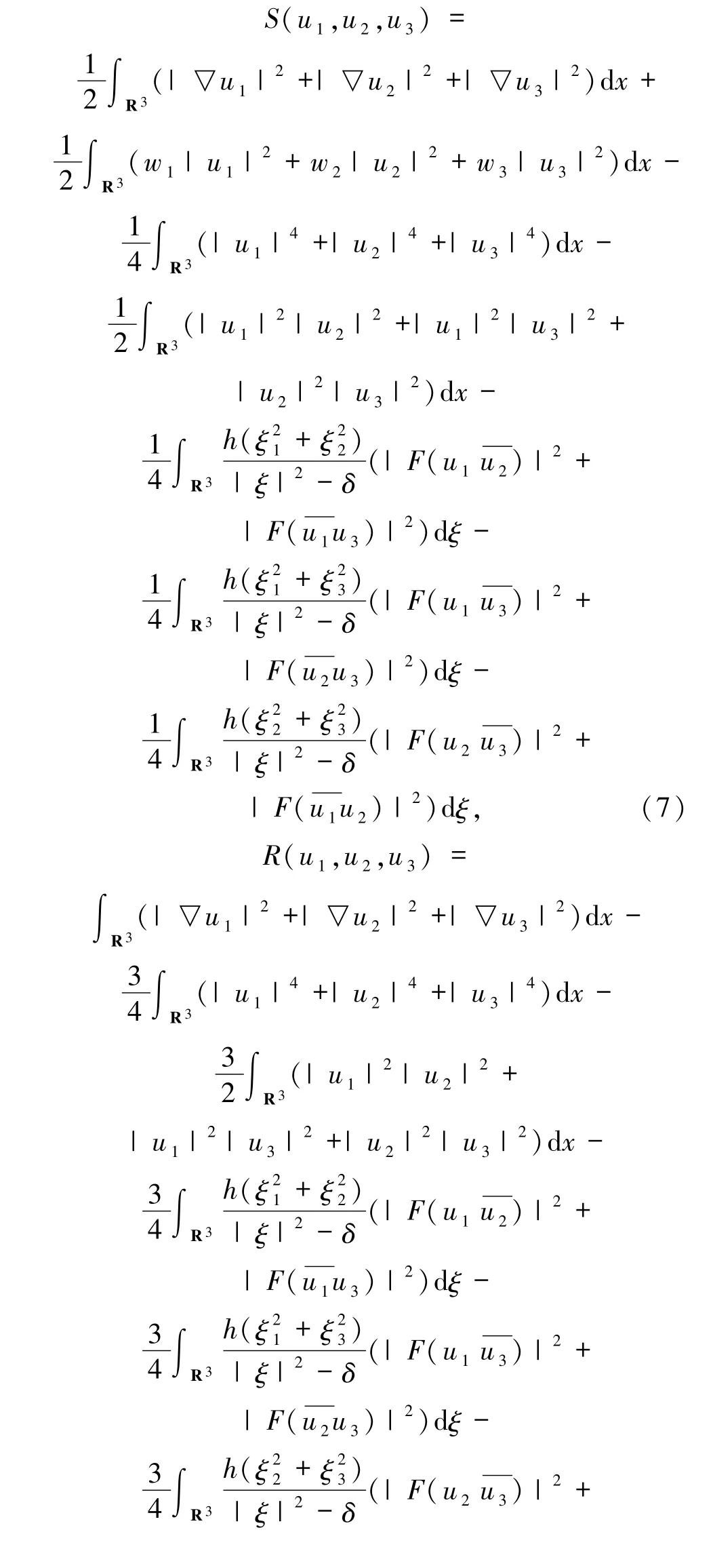
由Sobolev 嵌入定理和傅里叶变换，知S（u1，u2，u3）和R（u1，u2，u3）都是适定的.

此外，定义集合M为

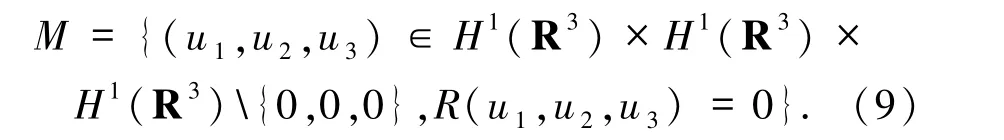
强制变分问题为

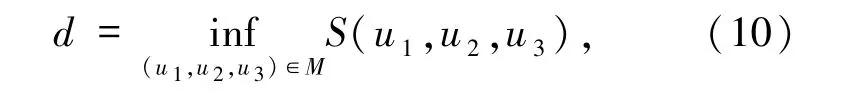
参见文献［9］，知道存在（Q，P，V）∈H1（R3）×H1（R3）×H1（R3）＼｛（0，0，0）｝满足

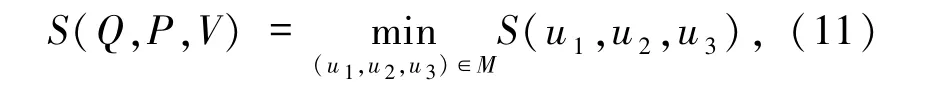
而以下结论成立.

引理1.1 由（11）式，则R（Q，P，V）＝0 且

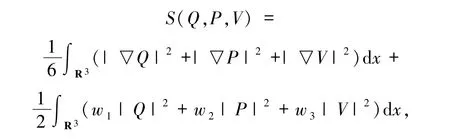
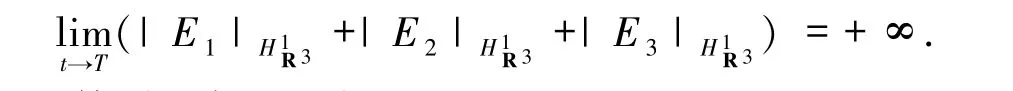
此外，得到以下引理.

引理1.2 令（E1，E2，E3）为柯西问题（1）～（4）的光滑解，则总质量和能量守恒

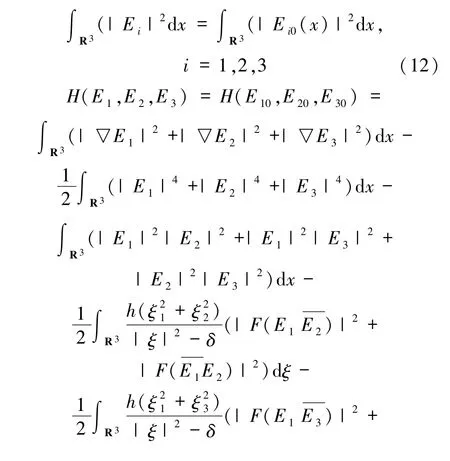
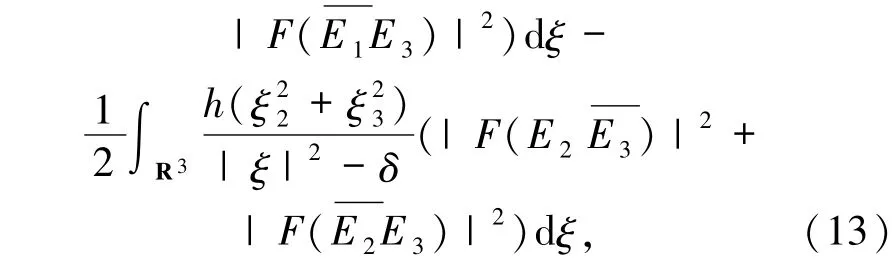
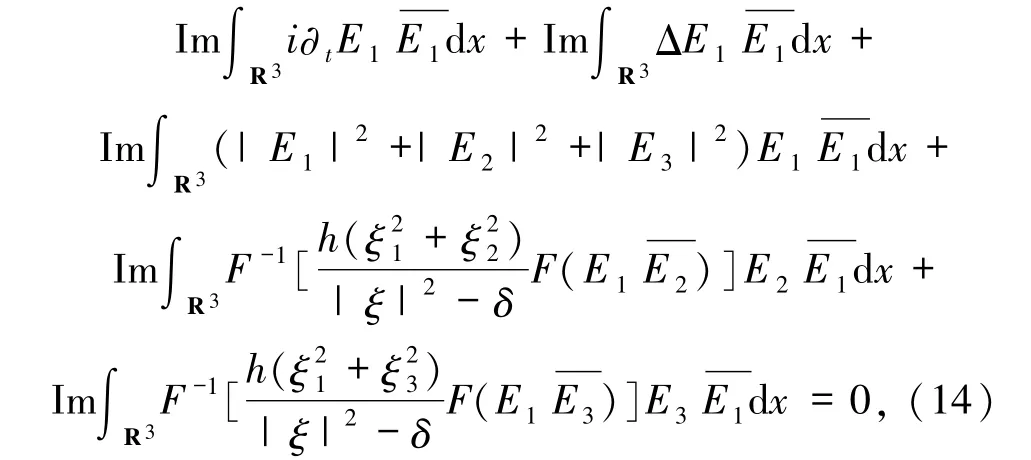
通过积分运算，则有

得到

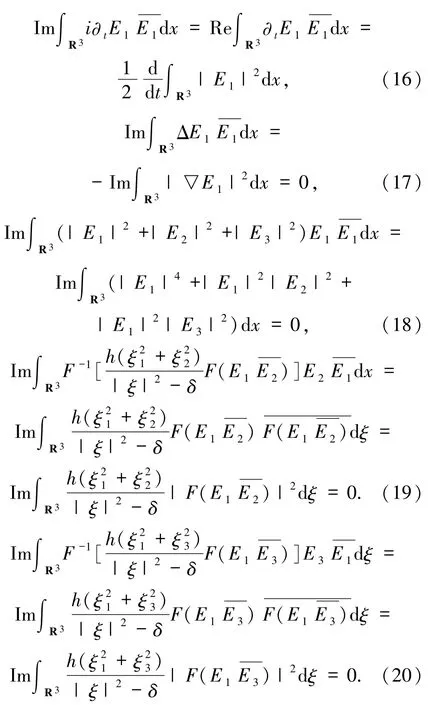
把（15）～（18）式代入（14）式，得到

同理可得

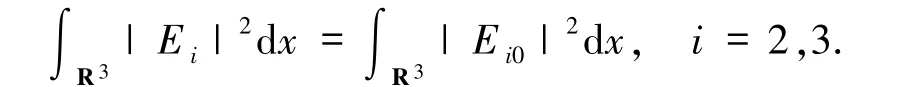
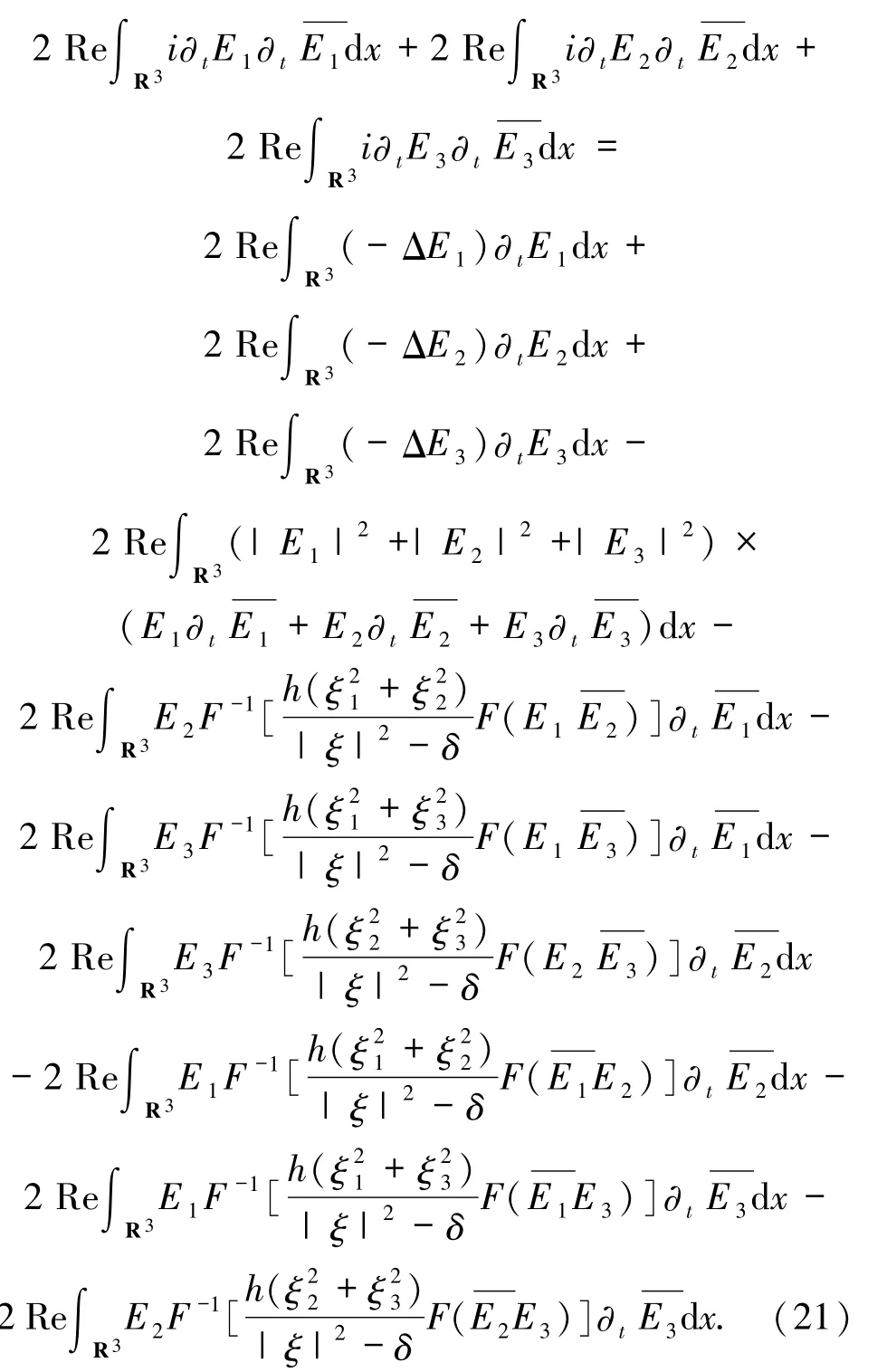
积分运算可得：

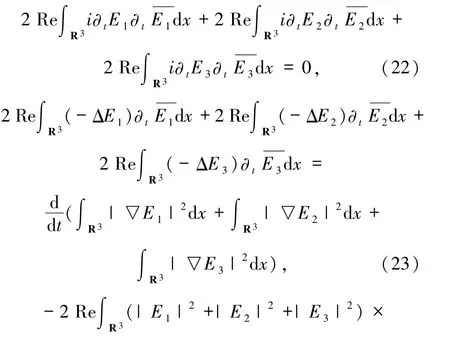
通过对（25）式积分运算，得到

把（22）～（27）式代入（21）式，得到

因此（13）式成立.

2 主要结果

令

命题2.1 令（E10，E20，E30）∈Σ 且（E1，E2，E3）∈C（［0，T］；Σ）为柯西问题（1）～（4）在［0，T）上的解.记

则

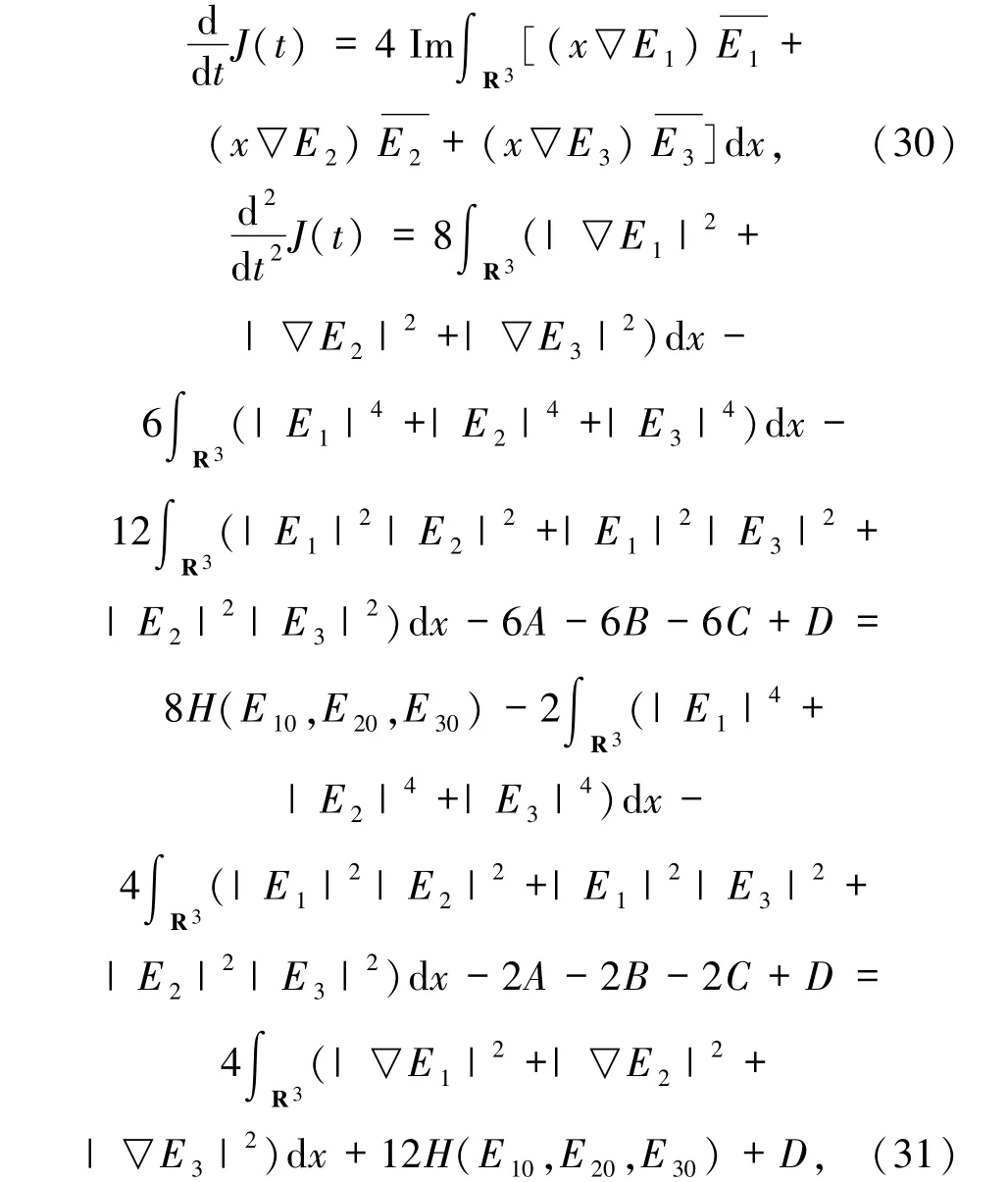
其中

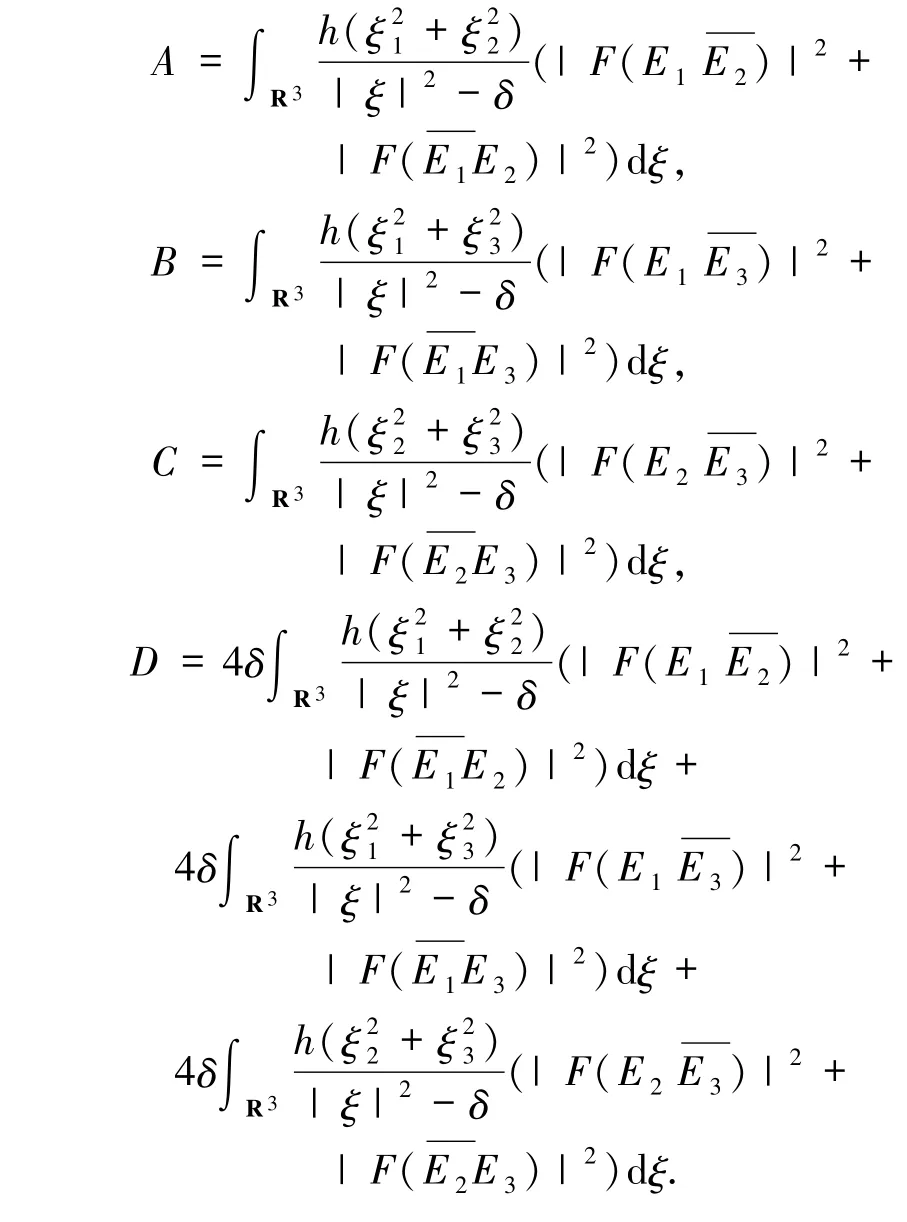
证明 因为（E1，E2，E3）∈C（［0，T］；Σ）是柯西问题（1）～（4）式在［0，T）上的解.由（E10，E20，E30）∈Σ 和文献［14］，有（E1，E2，E3）∈Σ.由（1）～（3）和（29）式可得

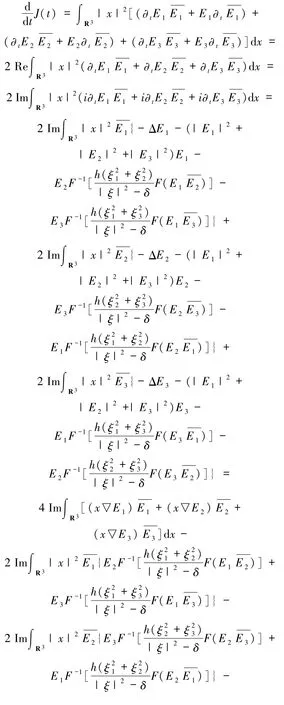
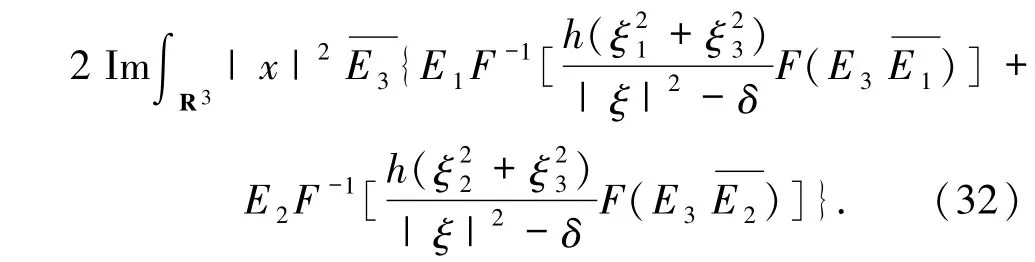
又因为

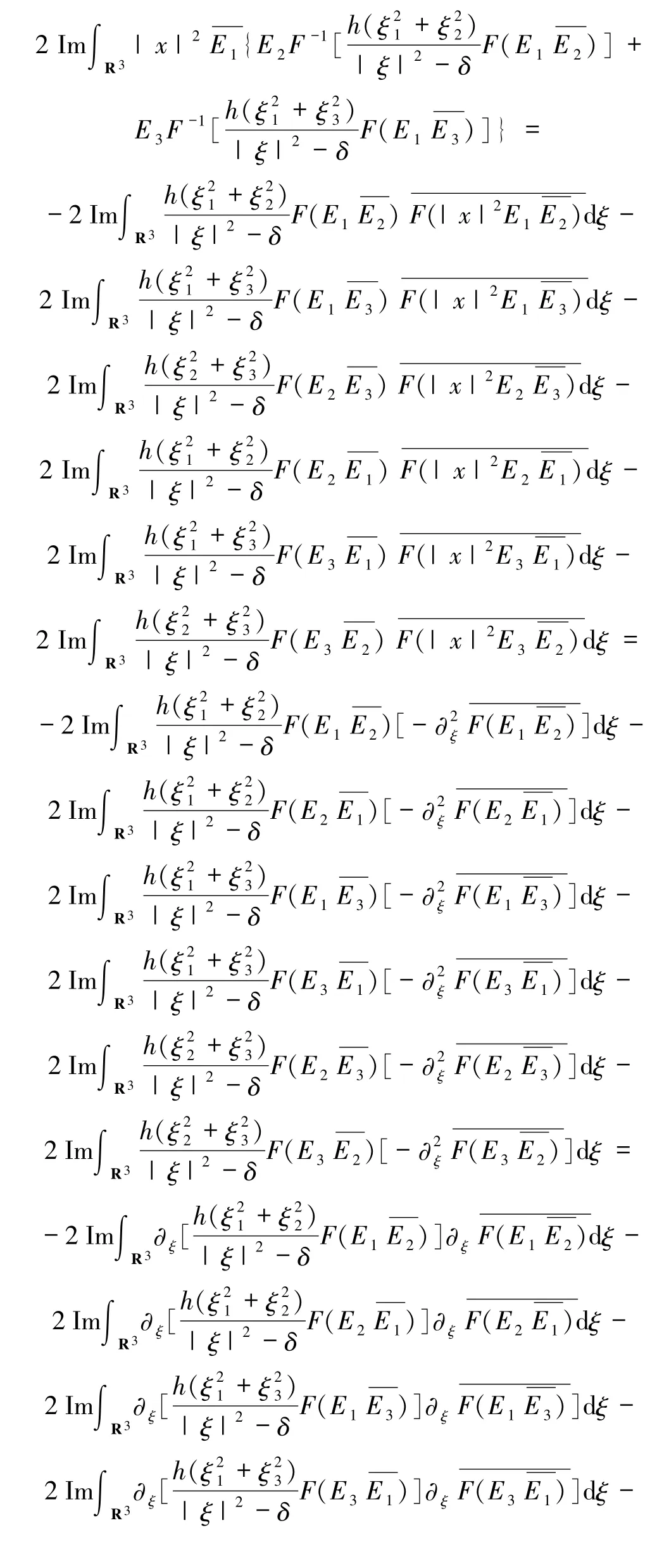
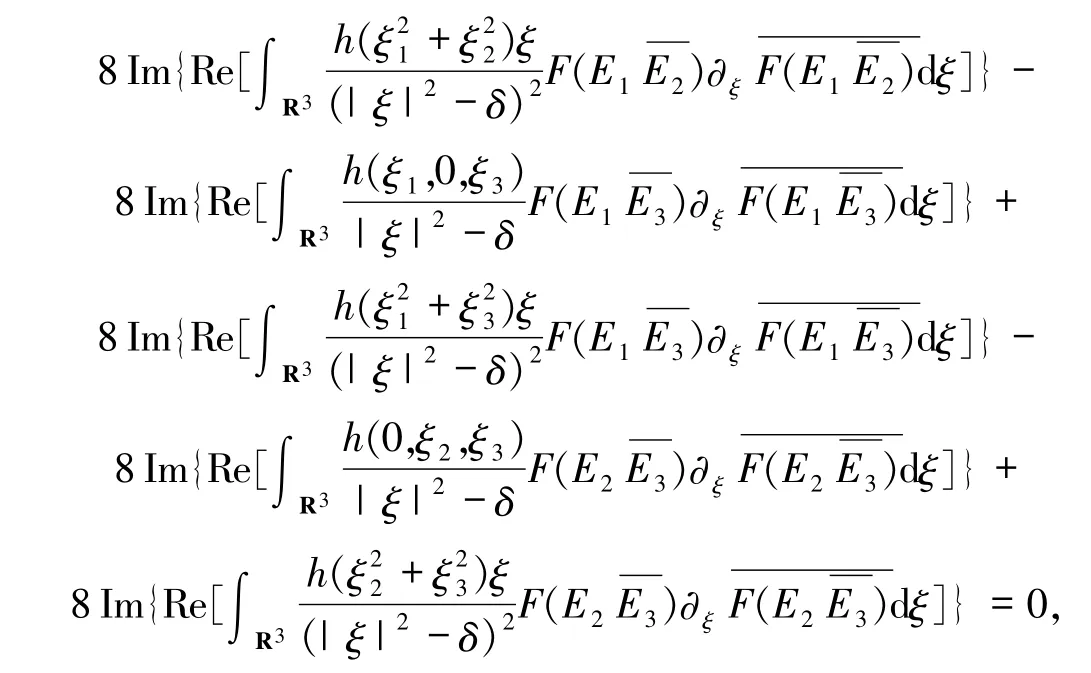
根据（32）式可得

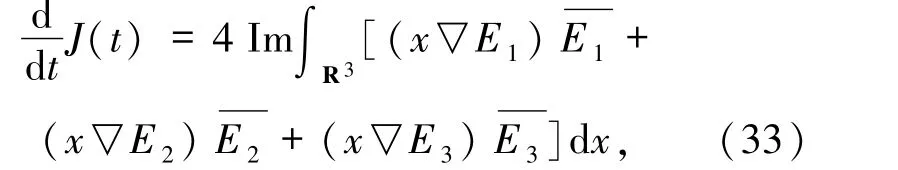
在（33）式中关于t求导，运用（1）～（3）式得到+

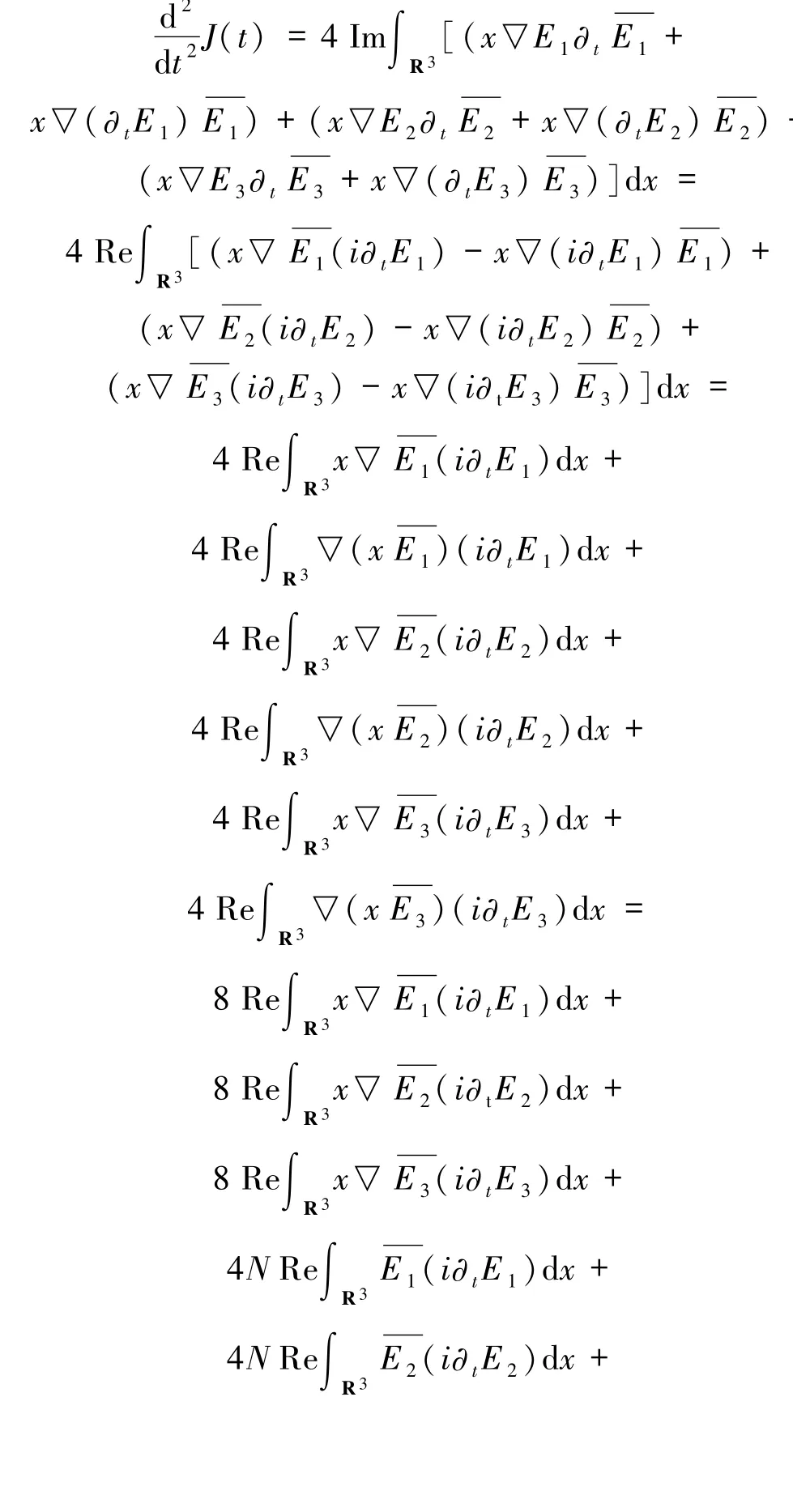
由（34）式积分可得：

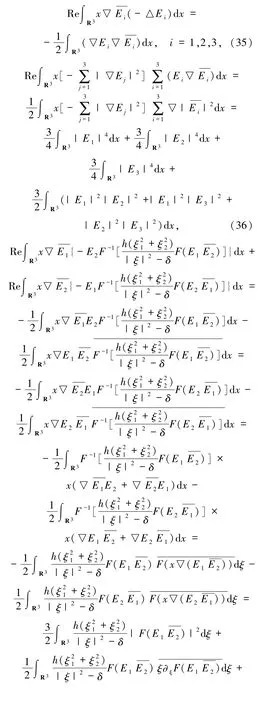
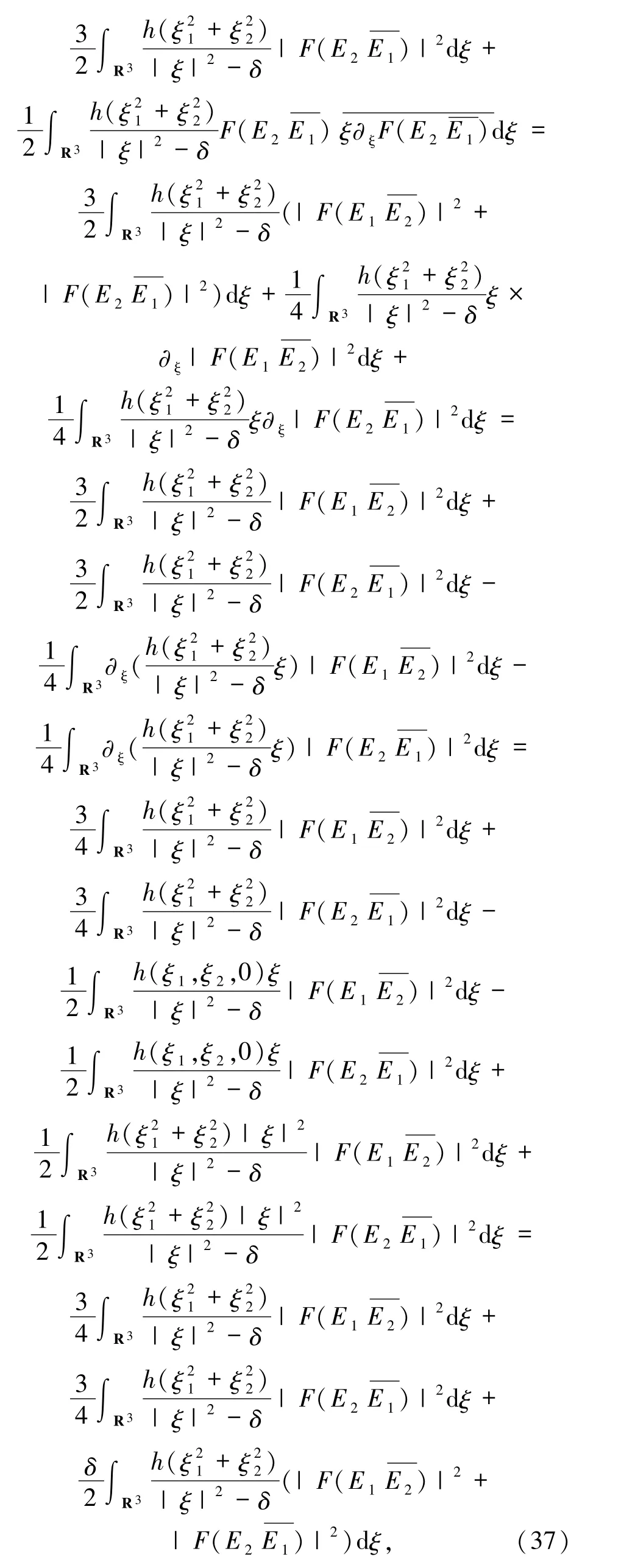
同理，（37）式通过积分运算得到

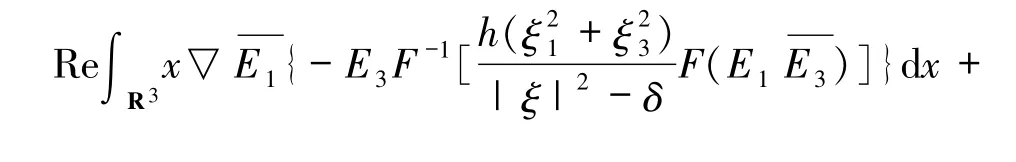
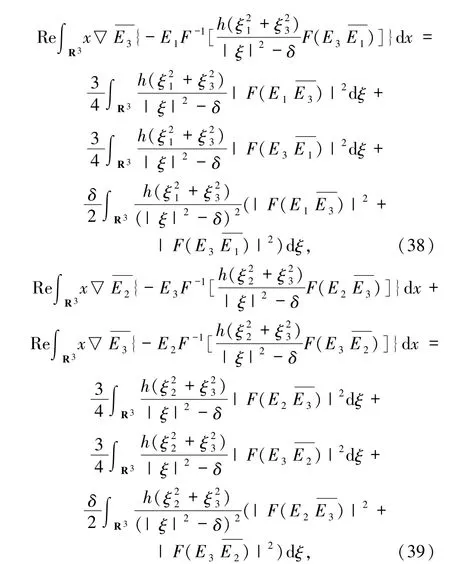
此外有

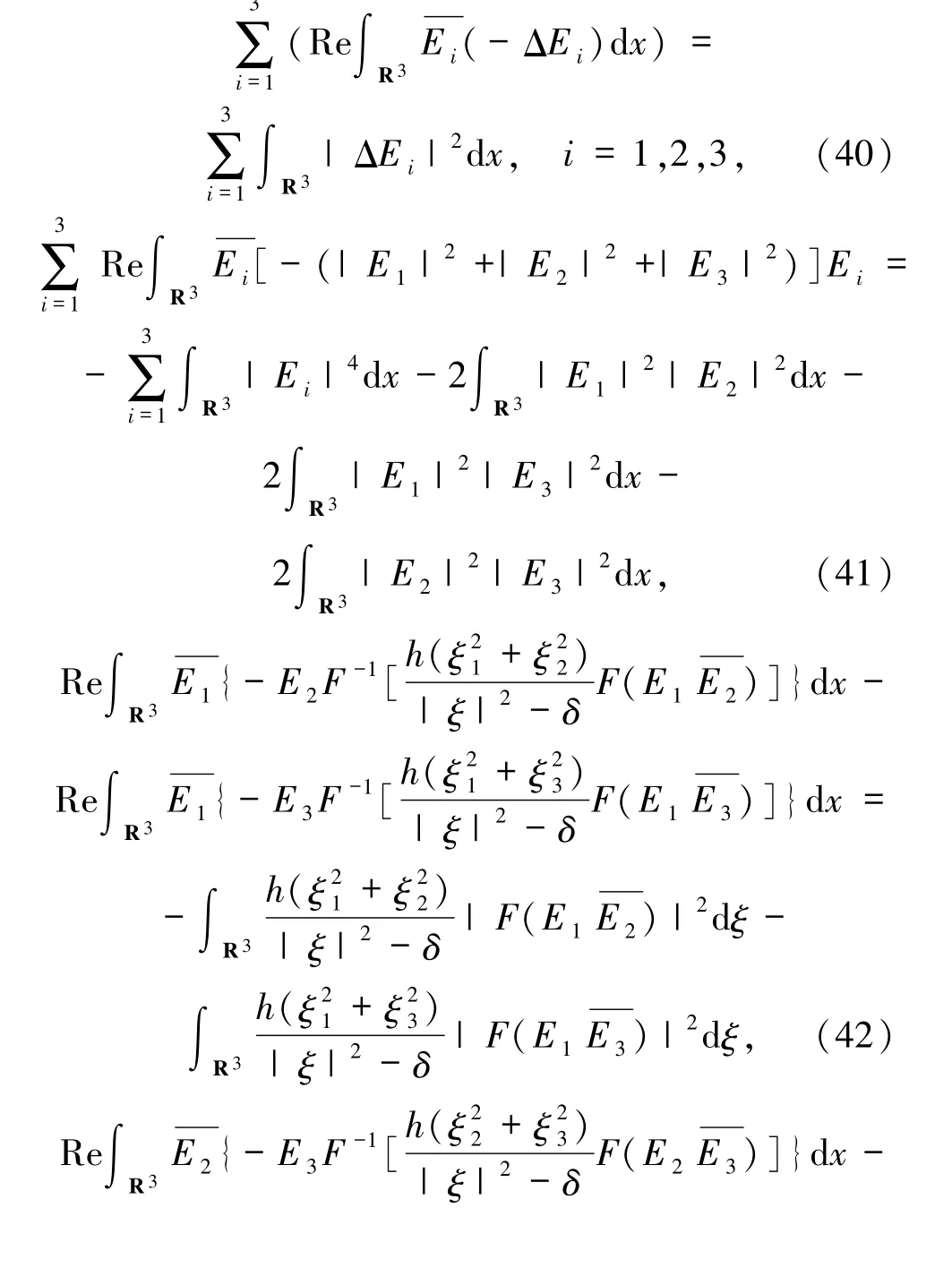
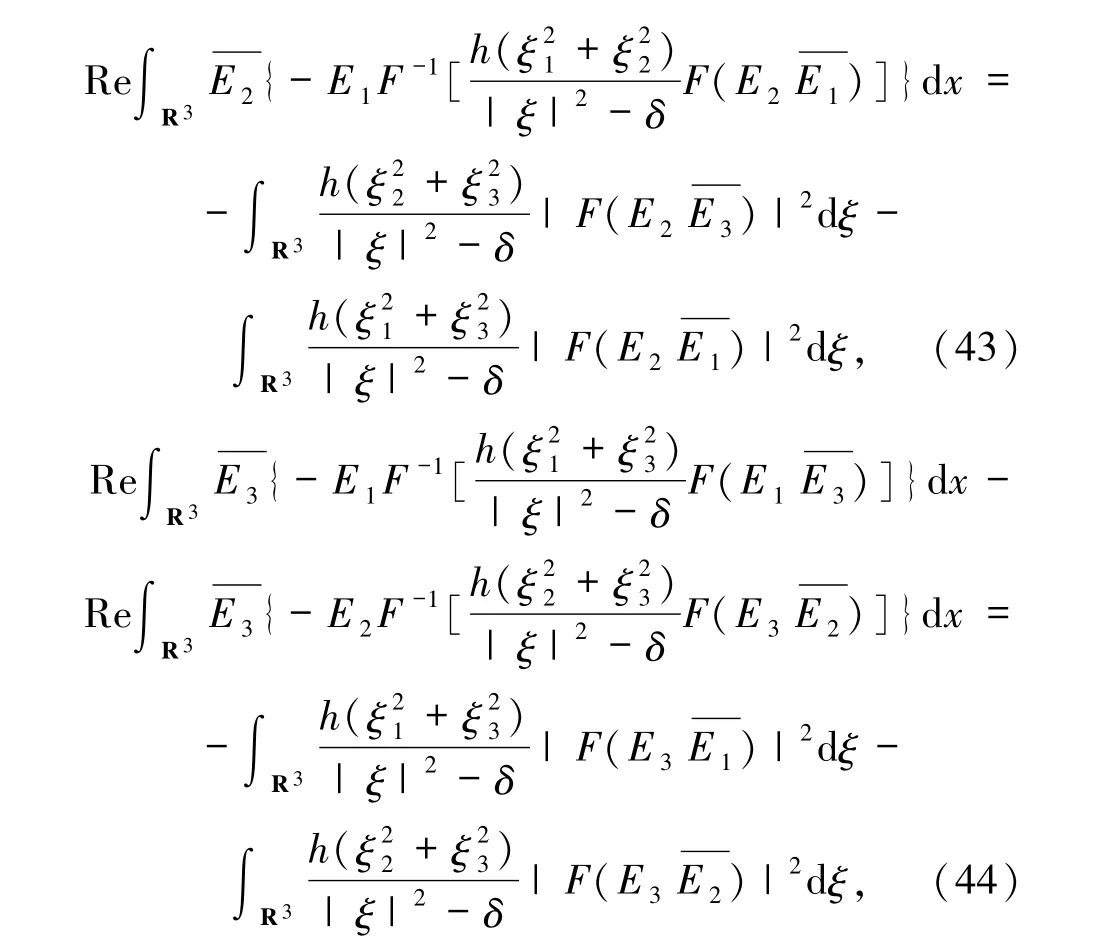
把（35）～（44）式代入（34）式可得

至此，命题2.1 的证明完毕.

参见文献［15］有如下引理.

引理2.1 令f是标量函数，如果｜x ｜f和▽f在L2（RN）中，则f在L2（RN）中并且满足

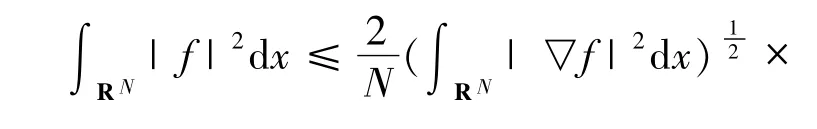
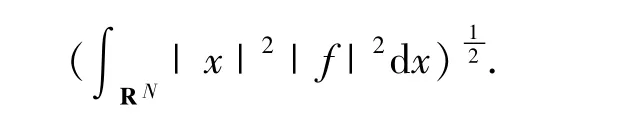
定理2.1 设（E1，E2，E3）为方程（1）～（4）的一类径向对称解且（E10，E20，E30）∈S，若

（i）H（E10，E20，E30）≤0；

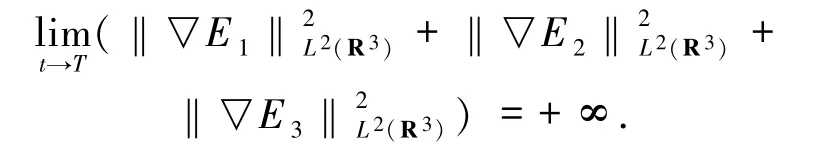
证明 令

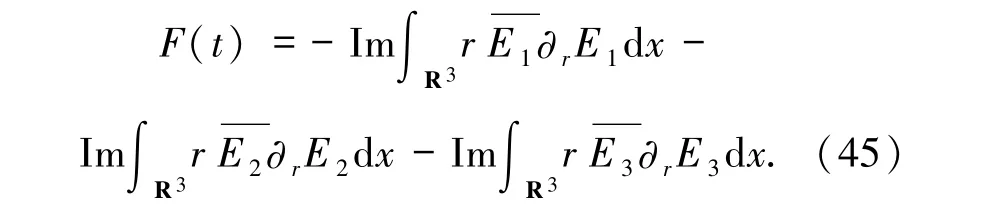
由（ii）可得F（0）＞0.此外，由命题2.1 有

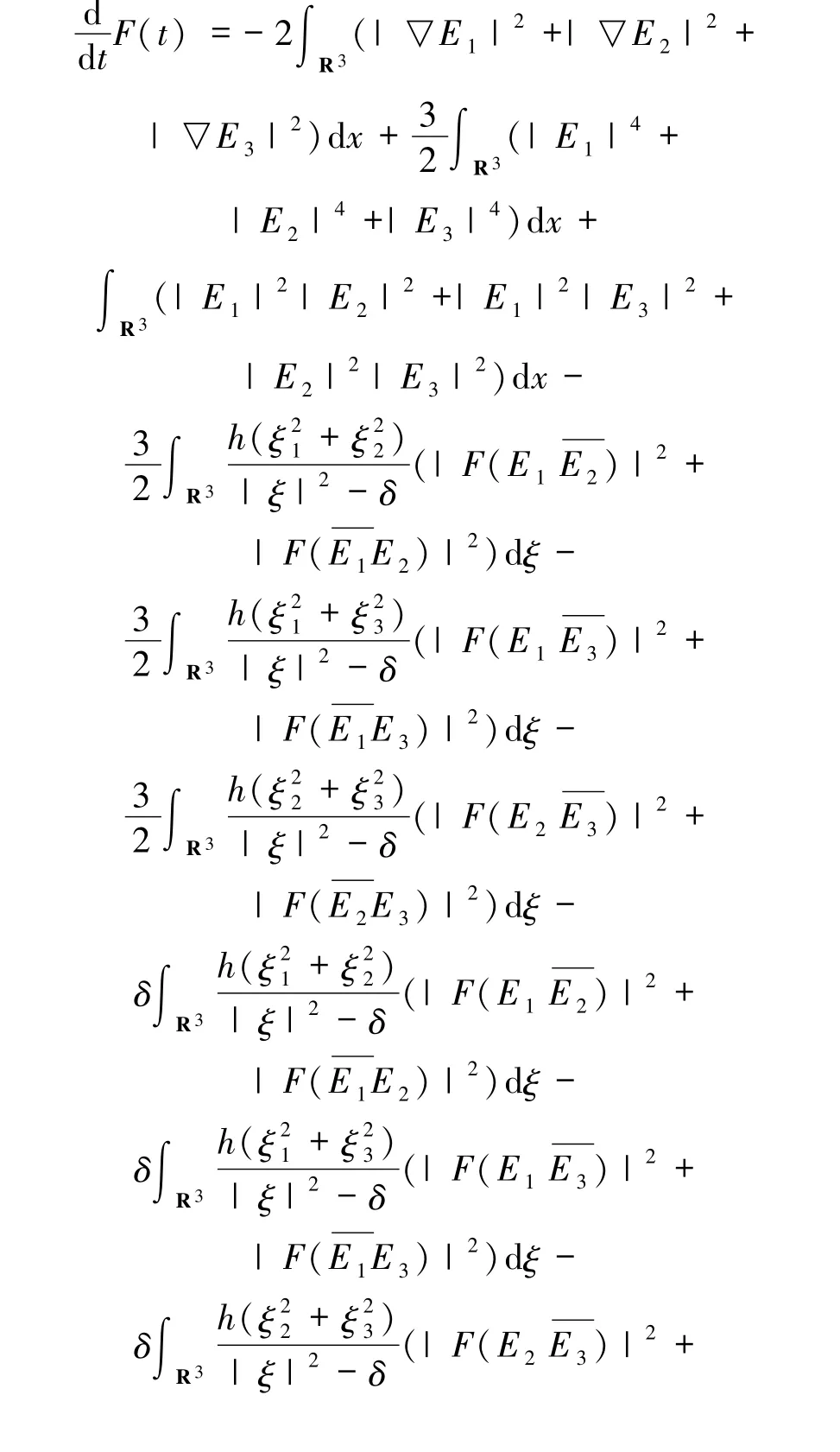
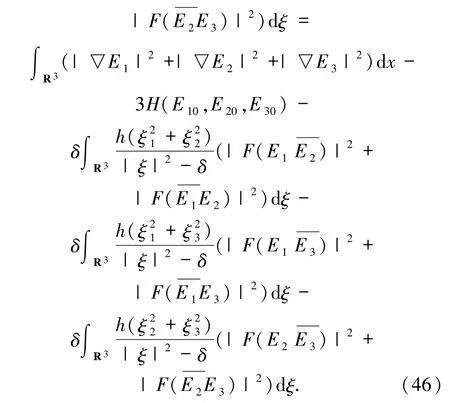
由于h ＞0 且δ≤0，（i）蕴含了

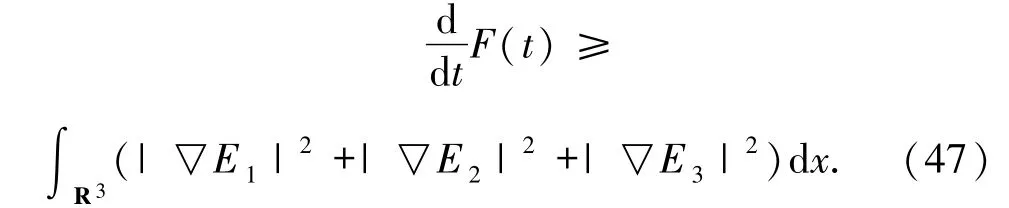
由F（0）＞0 和（47）式，可得F（t）＞0，由（E1，E2，E3）存在性和（30）式有

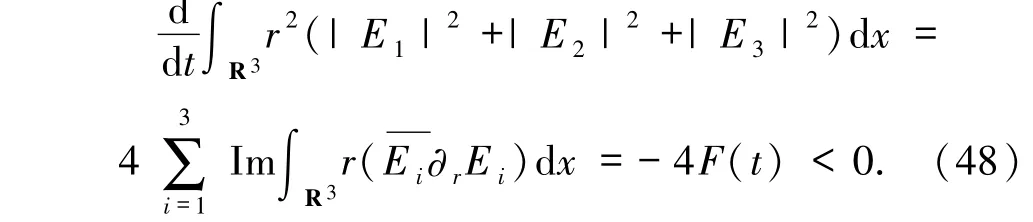
因此，

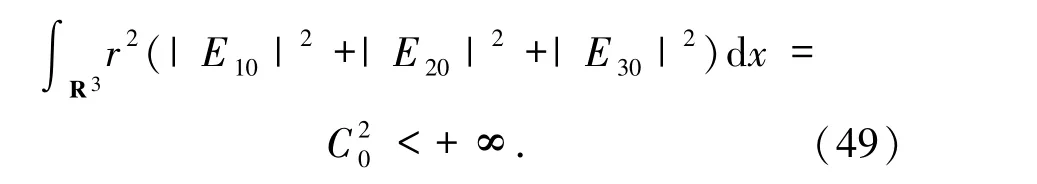
运用Schwarz不等式可得

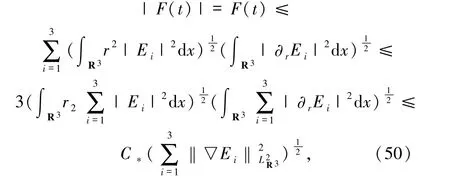
其中C*≥3C0.因此，由（47）和（50）式蕴含了

成立，从而

致谢 天津大学数学系的甘在会教授在论文写作过程中给予的指导与宝贵建议，谨致谢意.