数学实验,从问题开始
2020-05-25江苏扬州市四季园小学王兴伟
江苏扬州市四季园小学 王兴伟
数学实验是新课改后一线教师使用较广的一种方法,一个完整的数学实验主要包括“发现和提出问题、猜想或假设、设计和进行实验、分析和得出结论”等环节。数学课程标准提出:“要让学生在提出问题、分析问题、解决问题的过程中自主学习,享受学习的快乐。”那么如何在数学实验中恰当地引导学生发现和提出问题,使学生敢问、会问、善问呢?笔者在以下几方面做了尝试:
一、情境提问——因果策略
要培养学生的问题意识,首先必须激起学生的兴趣。创设趣味性的教学情境,促使学生自主、自愿地去想、去问,并且乐在其中。情境中蕴含着丰富的数学信息与问题,应用情境提问的策略就是让学生从情境中整理信息,提出要解决的问题,继而引导学生思考“为什么设置这样的情境”,从而去解决问题。
【案例1】 圆的认识
上课伊始,教师设计了一个与学生比赛的实验情境:全班挑选两个平时数学成绩最好、能力最强的学生,在黑板上用一个点固定一根线,老师和学生一起画圆,比赛谁画得又快又好。在全体学生热烈的加油声中,学生发现老师虽然慢条斯理却很快就画出了一个漂漂亮亮的圆,而全班选出的数学成绩最好的两个学生用了很长一段时间,始终画不出完整的圆。见此情景,有细心的学生很快发现了问题,大声提出“比赛不公平”,老师微笑问他为什么。学生拿起刚才的画圆工具说:“我们拿着的线是可以伸缩的,在画的过程中不能固定其长度。”教师由此引导学生思考,学生提出了一连串问题:“画圆为什么要固定一点”“这个点与圆有什么关系”“画圆的线为什么要不能伸缩”“不同长度的线画出的圆是什么样子”?在这种真实有趣的比赛情境中,隐含着对数学本质的探究。学生在这样的情境中,用数学的眼光发现数学问题,用数学的语言提出问题,问题意识不断增强。
二、 问题还原——比较策略
研究表明,当学生面对一个问题时,自觉或不自觉地会主动联系其已有经验,利用其已有经验中的表征方式进行同化。在数学实验中,可以让学生充分比较同一数学规律在不同情境下的应用,比较互相矛盾的解释、说法和理论,从中发现并提出问题。用此策略,当学生面对问题时,要充分调动其已有经验,对问题进行判断或选择,从而把问题还原到其已有的经验架构内,当不同主体经验碰撞时产生矛盾冲突,自然就形成新的问题,促使学生一探究竟,深入研究。
【案例2】两、三位数乘一位数笔算
在学习过两、三位数乘一位数笔算例题后,学生得出基本算法:数位对齐,从个位乘起。这个规定,大多数学生只是机械地记住了算法。课堂上,一个学生提出了这样的一个疑问:“两、三位数乘一位数,要从个位开始乘起,如果从最高位开始乘,是不是结果就不一样了呢?”听到这个问题,笔者灵机一动,先让学生猜猜看,结果发现有人认为不一样,有人认为肯定一样。
接着笔者提供了两个算式:34×2和132×3,学生通过计算比较,很快验证了猜想,得出了一致的结论:从个位乘起和从最高位乘起,结果一模一样,而且都很方便。这时候,又有学生提出:“既然结果一样,为什么还做这样的规定?”
在教师的启发下,大家纷纷建议,可以再写几个算式,自己试着再算一算。当每个学生分别从个位算起和从最高位算起后,经过比较,很快就发现问题了:“如果是不进位的乘法,随便从个位还是最高位开始,都很方便;但是如果是进位乘法,从最高位开始乘就不方便了。”于是,“进位乘法”的法则学生们通过计算实验,已经很明白了。通过比较,学生们不但知其然,并且知其所以然,为他们发现问题、解决问题提供了可能。
三、问题组块——扩大策略
数学实验中,教师要让学生在活动中多想想会遇到什么问题、为什么会有这些问题以及怎么解决问题,使学生自觉地经常把这些问题进行组块,形成一个“问题场”,学生置身“问题场”中不断得以浸染,在解决问题时,会不断产生“怎么办”“为什么这么办”等主动意识。教师要不断启发学生思考:从这个现象中总结出的规律,推广到更大范围或一般情况还能成立吗?这个规律是具有普遍性还是只适合于某些特殊情况?怎样改动才可以应用到另外的情况?教师在课堂教学中,要多问“为什么”,给学生表达思维过程的机会,培养学生的批判性思维,进而不断发现问题,学会提问。
【案例3】钉子板上的多边形
教师首先让学生观察图1,提出问题:这4个多边形的面积与每个多边形边上的钉子有什么关系?你能用一个关系式表达吗?学生通过观察、计算, 很快概括出规律:用S表示面积,n表示钉子数,S=n÷2。
然后教师呈现3幅图,如图2,让学生数出它边上的钉子数和面积数,快速验证,并思考有什么问题。结果学生发现,前两个符合这样的规律,第三个不符合,从而产生新问题:为什么有的符合,有的不符合呢?经过观察比较,学生发现:这个规律必须满足“内部有a枚钉子,a=1”这个条件,也就是a=1时,S=n÷2才成立。
教师接着启发学生:这个规律推广到更大范围还能成立吗?让学生分组研究多边形里面有2枚钉子的规律。学生通过和小组成员先画一画、数一数、算一算,发现当a=2时, S=n÷2+1,教师相机板书。
至此,学生的思维已经被激活,他们马上会思考:a=3有怎样的规律?a=4呢? a除了可以是1、2、3、4,还可以表示什么?有什么方法去验证呢?学生通过分组实验,很快验证了这些结论。教师将这些公式一一进行板书,启发学生:你能用一个式子将这么多式子概括出来吗?学生通过抽象,自然得出:S=n÷2+a-1。
在以上的过程中,教师设计了层层递进、环环相扣的问题组,由表及里,不断地引领学生向数学规律的本质挺进,学生在“提出问题—解决问题—又提出新问题—再解决问题”的循环往复中,充分经历了数学建构的过程,感受到了数学学习的有趣好玩与挑战性,点燃了思维的火花。
四、反思拓展——变化策略
每一次的数学实验活动都是学生探究学习的“加油站”,每次活动的结束只是又把学生带到另一个新的起点,因此教师对于每次实验都要做好反思与拓展,让学生能主动认识到活动中存在的问题,以及为什么会出现这样的问题。教师要经常引导学生思考:在通常情况下成立的理论与规律,放到极端条件下还会出现或成立吗?会不会出现新的问题?正面的问题,反过来会怎样?这个结果还有没有其他的结论?如果条件改变,结果会怎样?从而不断内化认识,积累并升华学生提出问题的经验。
【案例4】奇妙的百分率
教师首先分别出示小明和小华第一阶段和第二阶段比赛的表格。让学生观察在第一阶段和第二阶段,谁的命中率高。学生观察后得出:两个阶段,小明的命中率都比小华高。
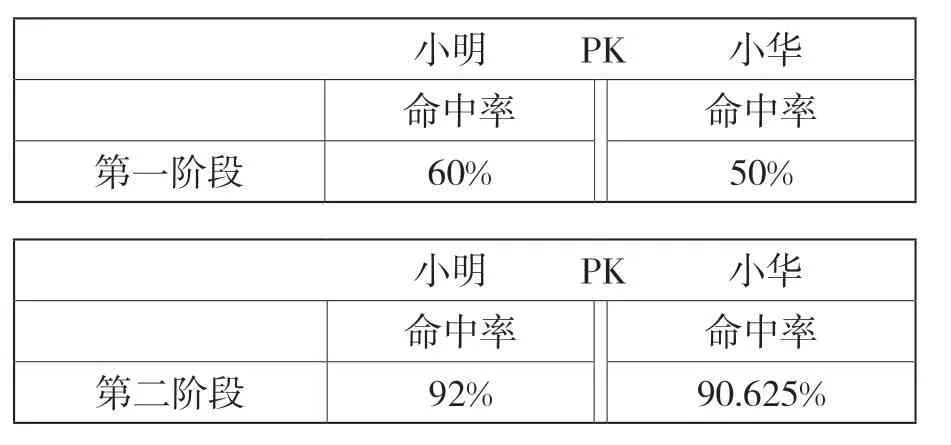
小明 PK 小华命中率 命中率第一阶段 60% 50%小明 P K 小华命中率 命中率第二阶段 92% 90.625%
然后,教师将上面两个表格合二为一,提出:将两阶段投篮的情况结合起来考虑,你认为谁投篮的命中率高?这时,学生几乎不假思索,一致都认为:仍然是小明命中率高。只有个别学生表示怀疑,但也说不出理由。

小明 PK 小华命中率 命中率第一阶段 60% 50%第二阶段 92% 90.625%
接着,教师完整出示如下表格,引导学生观察后思考有什么问题。有了具体的数据支撑,学生马上就提出:小华两阶段的投篮命中率都比小明低,总的投篮命中率却超过了小明,这是为什么?
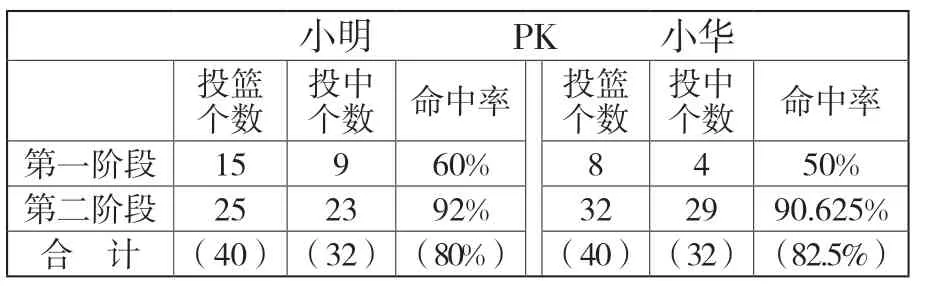
小明 P K 小华投个篮数投个中数 命中率 投个篮数投个中数 命中率第一阶段 15 9 60% 8 4 50%第二阶段 25 23 92% 32 29 90.625%合 计 (40)(32)(80%) (40)(32)(82.5%)
教师让学生先将想法写下来,在小组内交流,再组织全班讨论。通过交流,学生会发现:小华命中率低的时候投篮个数非常少,而命中率提高的时候投篮个数却很多,小明两次投篮的个数相差不大。阶段比赛的单位“1”不同,仅靠这两个阶段的命中率不足以准确判断,只有比较总命中率才能正确判断。
这里,当学生的已有知识经验与眼前的情境发生冲突时,往往会引起学生的关注和探索,通常成立的规律,为什么放到这里不成立呢?此时学生在心理上产生填补这些空白的强烈欲望,教师及时抓住学生的迫切心理,让学生自主探究,往往会收到超预期的教学效果,学生的问题意识会得到明显的提升。
五、激励评价——量化策略
美国心理学家罗杰斯认为,“成功的教学依赖于一种真诚的理解和信任的师生关系,依赖于一种和谐安全的课堂气氛。”教师要正确对待学生的提问,发掘其可贵之处,建立一套合适的激励评价策略。
首先,教师要注意在师生间建立平等、民主、亲切、和谐的关系,用风趣、幽默的语言,亲切和谐的笑容,为消除学生心理障碍创设良好氛围。
其次,在课堂教学中,教师要做到当学生提出的问题不符合要求时,教师也同样要给予鼓励;当学生在提出问题的过程中,由于紧张或考虑不充分而词不达意、语无伦次时,教师也要认真倾听,不能打断学生的发言;当学生提出错误的问题时,教师也不能嘲笑、讽刺、指责。一句话,要让学生在课堂上能够“自由地呼吸”,敢想、敢说、敢做,能充分表达自己的见解。
第三,教师可以设计一张表格,根据表格中学生的行为,定期请小组互评,作为平时成绩评定的依据。有了行为指标,学生的行动就有了指南和方向。
笔者根据对学生平时的观察,制定了下列量表:
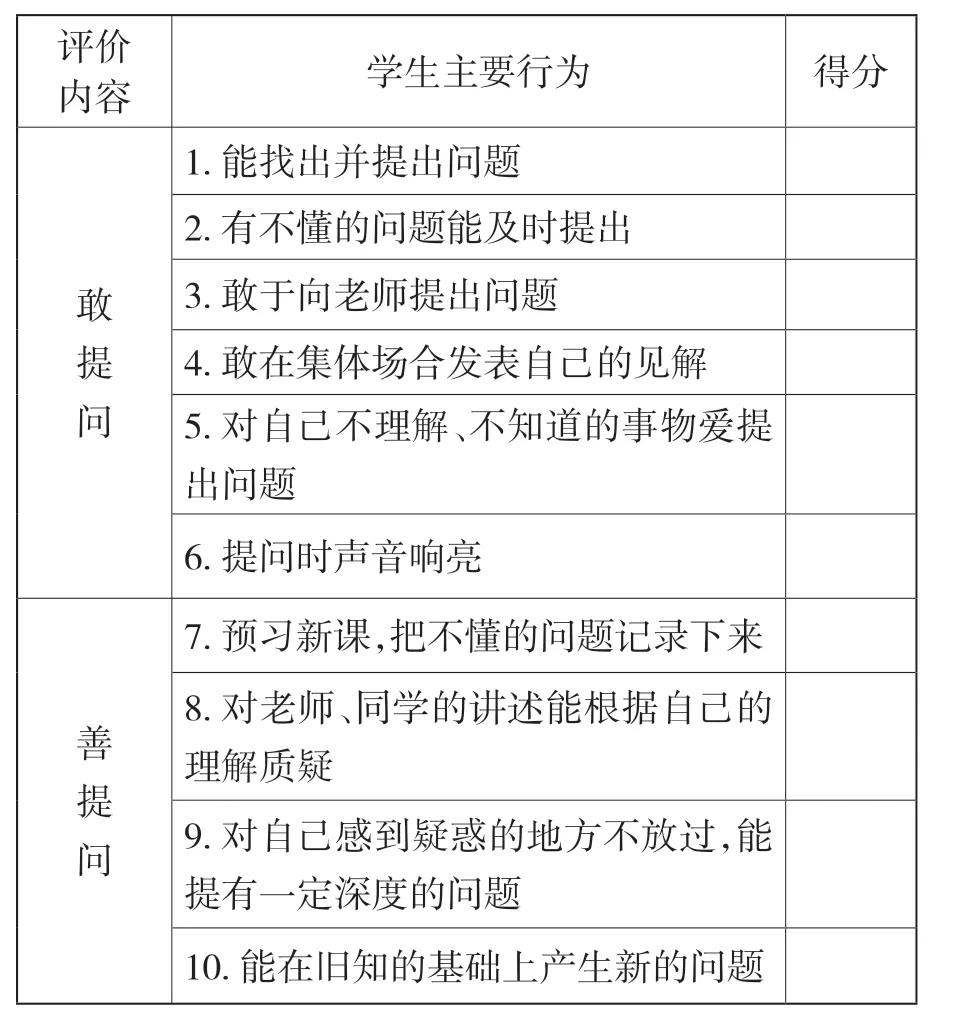
评内价容 学生主要行为 得分1.能找出并提出问题2.有不懂的问题能及时提出敢3.敢于向老师提出问题提4.敢在集体场合发表自己的见解问5.对自己不理解、不知道的事物爱提出问题6.提问时声音响亮7.预习新课,把不懂的问题记录下来善提问8理9提..对解 对有老质 自一疑 定师 己深、 感同度到学的疑的问惑讲题的述 地能 方根 不据 放自 过己 ,的 能10.能在旧知的基础上产生新的问题
在教学中,教师要根据学情和教材特点,灵活使用上述策略。在数学实验活动中,教师还要充分引导学生在实验中开展猜想、假设、实验、比较、分析、论证、评估、交流等活动,这样才能有效地激发学生发现问题、提炼问题、分析问题、解决问题的意识;强化学生“问题意识”,进而全面提升学生核心素养。
