作战兵力数量系统动力学研究
2020-05-24齐小刚翟豆豆刘学星
齐小刚,翟豆豆,刘学星
(1.西安电子科技大学 数学与统计学院,陕西 西安 710071;2.中国电子科技集团有限公司数据链技术重点实验室,陕西 西安 710068)
随着各国军事力量的不断壮大,现代战争已成为作战体系与体系之间的对抗[1],一体化联合作战是现代战争的基本作战样式。两方作战,考察的不仅是彼此的武器装备,更是对由双方的武器装备、人员配备所组成体系的整体力量的衡量,军种间的支援配合在现代战争中的作用日益凸显。观察、判断、决策、行动(Observe,orient,decide,and act,OODA)作战环模型用不断往复循环的“观察、判断、决策、行动”来描述战场上的指挥过程[2,3]。它是一个严格的闭合环路,每次作战行动都可以看成一个OODA循环过程。系统动力学是一门认识和解决系统问题、分析和研究系统内部信息反馈机制的学科[4],是定量模型与概念模型的统一,被广泛应用于各种类型反馈系统的研究与管理。
在OODA环的基础上,用系统动力学研究体系作战可以明确地反映体系内部的反馈关系。李大亮等[5]利用OODA环理论对信息化战场信息安全保障过程进行分析,用系统动力学方法对其进行建模仿真。韩潇弘毅等[6]对协同决策的结构、参与者和信息反馈关系进行分析,构建了基于系统动力学的协同决策模型。申普兵等[7]从信息流转的角度研究了作战指挥流程,运用系统动力学方法构建了体系对抗下作战模型。黄建明等[8]基于OODA作战环理论,利用系统动力学构建了信息化条件下的作战对抗模型。
本文在前人研究的基础上,探讨红蓝作战中的兵力数量变化问题,主要是基于系统动力学,采用OODA环描述红蓝双方作战中的对抗过程,建立双方作战的系统动力学模型,探索观察环节的因素对作战结果的影响,以及OODA环中的其他因素对这种影响是否有改变,对OODA环中影响红蓝双方作战结果的因素进行分析讨论。
1 系统动力学建模过程
系统动力学模型的构建是研究系统问题的关键环节,建模过程是一个有序、科学、严密的过程,也是一个在提出问题、产生假设、数据搜集、写方程、测试、分析之间的持续反复过程[9,10]。在建模过程中不断地深入问题本身,洞察模型的各种细节,并适当做出简化,才可以在清楚定义问题的同时解决问题。
对于作战问题,战争中的任何一方都想在击败敌方的同时使己方的兵力数量损失尽可能少,分析可知,本文建模目的是为了分析作战中双方兵力数量的变化情况。整个作战过程包括指挥、准备、部署、协同、保障等环节,所涉及的变量众多,不可能对全部变量加以考虑,本文的模型是在OODA环的基础上构建的,仅需要选出与观察、判断、决策、行动相关的变量进行研究分析。
系统动力学模型中有状态变量、速率变量、辅助变量以及常量,与OODA环相关的变量有兵力数量(状态变量)、损耗率(速率变量)、决策能力(辅助变量)、决策时间(常量)等,有必要对这些系统内部要素进行定义与分类。系统内部要素之间存在因果反馈关系,如损耗率越大,兵力数量下降越快,需要对变量进行逻辑分析,绘制它们的因果关系图以及存量流量图。在对系统变量反馈因果关系研究的基础上,分析变量之间线性、非线性或脉冲的数学关系,建立它们之间的数学模型,在存量流量图中输入数学方程,完成系统动力学模型的建立。对已经构建的模型,不断调整其中的变量参数,包括常量的数值、辅助变量中的参数、状态变量的初始值等,进行仿真模拟,并根据具体的仿真情况对模型中不合理之处进行适当修改,给出恰当合理的解释。
运用系统动力学理论解决实际问题是一种直观且便捷的方式,它可以对作战中的定性指标进行分析,描述作战环节中各因素的复杂相互关系,设置程序化的建模过程,采用简单易行的模型调整方式,具体流程如图1所示。
2 系统边界的确定
由于认知的局限性以及作战系统涉及的变量众多,无法对全部变量进行分析,建模时需对系统的边界进行界定[11]。假定外部环境因素的变化不会引起系统内部因素的变化,同时也不受内部动态行为的控制。本文仅考虑红蓝双方对抗作战,不讨论复杂的社会、政治、经济条件对兵力数量、作战方式、决策能力等的影响。
首先,对于红蓝双方作战兵力数量变化问题,主要是围绕着双方作战展开,作战中任何一方都想击败对方,同时使己方的兵力数量损失尽可能少,又因OODA环可以用来描述双方的对抗过程,故基于OODA环的红蓝双方作战之间的相关关系是研究重点。OODA环中的观察、判断、决策、行动环节都是最为关注的内容。
其次,划分系统边界时,系统内部的反馈回路需为一个完整的闭合回路且界限封闭,这样才能准确地研究模型中各个因素之间的相关关系以及该关系对系统动态行为的影响。OODA环中的观察、判断、决策、行动本身就是一个完整的闭合回路,又因为红方的行动会影响蓝方的观察和行动,蓝方的行动会影响红方的观察和行动,由此可以形成其他闭合回路。
基于以上两点,红蓝作战的系统边界如图2所示。
3 红蓝作战的系统动力学模型
3.1 因果关系图
因果关系图是系统动力学中用来表示系统反馈结构的重要工具,它是由变量以及表示变量之间因果关系的箭头所组成。本文的研究对象是OODA作战环下的红蓝双方作战兵力情况,红蓝双方对抗是模型中的关键环节,因果关系主要是以OODA环为基础展开,详细描述了红蓝双方在对抗中的相互影响关系以及红蓝双方自身的影响因素,由此绘制的红蓝双方作战因果关系如图3所示。
3.2 存量流量图
对红蓝双方作战的因果关系进行分析,构建OODA作战环下的红蓝双方对抗存量流量图,并建立变量之间的数学方程式,完成红蓝双方对抗的系统动力学模型的建立。依据存量流量图中的4种变量类型,在Vensim PLE环境下构建存量流量模型,如图4所示。
3.3 数学方程式
红蓝双方除探测获取信息的速度有差别外,其他变量均一致。
根据存量流量的定义,存量是数量对时间的积累,由流量来决定,可以得到红方兵力数量与其损耗率的数学方程式为
式中:Nr(t)为红方兵力数量,rr(t)为红方的损耗率。兵力数量由于损耗而随时间减少。
红方的损耗率与红方兵力数量、蓝方兵力数量、蓝方对红方的损耗系数以及蓝方的决策能力之间的数学方程为
rr(t)=α×Db(t)×Sr(t)×Nr(t)×Nb(t)
式中:rr(t)为红方的损耗率,α为常数项系数,Db(t)为蓝方的决策能力,Sr(t)为蓝方对红方的损耗系数,Nr(t)为红方的兵力数量,Nb(t)为蓝方的兵力数量。
红方综合判断能力是由红方观察能力和红方综合判断的准确率决定,由于管理者接收到观察的信息后,进行判断需要一定的时间,会造成延迟,由此得到红方综合判断能力的数学方程式为
Zr=GYr×PZr
式中:Zr为红方综合判断能力,GYr为经过一定时间延迟后的红方观察能力,PZr为红方综合判断的准确度。
红方获取有效信息的速率是由红方探测获取信息的速度和蓝方阻止红方获取信息的速度共同决定,它们之间的数学方程为
Vr=VTr-VZr
式中:Vr为红方获取有效信息的速率,VTr为红方探测获取信息的速度,VZr为蓝方阻止红方获取信息的速度。
红方观察能力的数学方程式为
Gr=Xr×Kr
式中:Gr是红方的观察能力,Xr是红方获取的信息量,Kr为红方获取信息的可靠性。
红方探测获取信息是由电子设备完成,为了防止被蓝方检测到,需要间断性的探测,为了表示这种周期性的状态,可以用一个多脉冲函数来表示红方探测获取信息的速度,则数学方程式为
VTr=α×f
式中:VTr为红方探测获取信息的速度,α为常数项系数,f是一个多脉冲函数。
模型中常量的初始值设置如表1所示。
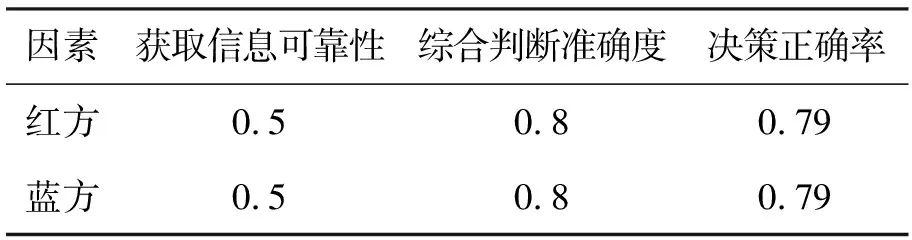
表1 常量初始值
4 仿真实验及结果分析
4.1 初始仿真结果
不妨假定红蓝双方作战的总时长为350 min,对第3节所建模型进行仿真实验,可以得到作战过程中红蓝双方兵力数量随时间的动态变化过程,初始仿真参数下的作战仿真结果如图5所示。
在保证红蓝双方其他变量相同的前提下,仅使它们探测获取信息的速度有所差异,得到的模型仿真结果如图5所示,从图5可以看出,红蓝双方的兵力数量都呈现一个递减的趋势,但是蓝方兵力数量的下降趋势明显快于红方,且在蓝方兵力数量接近于0时,红方的兵力数量处于一个比较稳定的状态,这是因为蓝方兵力趋近于0时,基本丧失战斗力,不会再对红方造成损伤,因此红方的兵力数量基本保持恒定,与实际情况相符。由此可知,红方探测获取信息的速度越快,红方的观察能力也会越强,从而使红方在OODA环上占据优势,率先破坏蓝方的OODA循环过程,使蓝方被动应战,蓝方兵力损伤的速率快于红方。
从仿真模拟中还可以得到红蓝双方具体的作战结果,如表2所示。
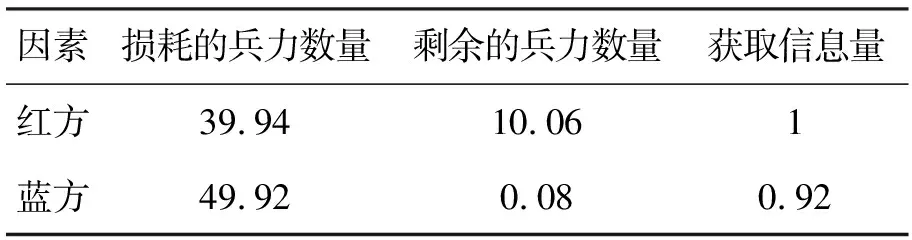
表2 红蓝双方作战结果
从表2可以看出,红蓝双方作战结束时,红方累积获取的信息量为1,达到了最高值,且从图5中可以看出,红方在300 min左右已经达到最高,而蓝方在战斗结束时为0.92,且一直处于累积的状态;红方在作战结束时,大约剩余1/5的兵力,而蓝方几乎全部战毁,可见获取信息量的多少会影响战争的最终结果。
4.2 实验分析
从上述分析可知,由于蓝方获取信息的速度较慢,只能处于被动应战状态,致使兵力数量下降较快,蓝方如果想要改变这种状态,就需要调整蓝方OODA环中的其他因素,即改变蓝方决策的正确率、蓝方综合判断的准确度以及蓝方观察信息的可靠性等某一个变量,分析其变化对红蓝双方兵力数量变化的影响。
(1)调整蓝方决策正确率:在初始模型的基础上,仅改变蓝方决策的正确率。经过反复模拟仿真,发现随着蓝方决策的正确率提高,红蓝双方的兵力数量下降趋势越来越接近,在蓝方决策的正确率从0.79提高为1时,红蓝双方的兵力数量变化曲线完全重合,仿真结果如图6所示。
(2)调整蓝方综合判断准确度:在初始模型的基础上,仅改变蓝方综合判断的准确度,对其进行多次调整。当蓝方综合判断的准确度从0.8提高为1时,红蓝双方的兵力数量下降趋势基本重合,仿真结果如图7所示。
(3)调整蓝方获取信息的可靠性:在初始模型的基础上,仅改变蓝方获取信息的可靠性,对其进行多次调整。当蓝方获取信息的可靠性从0.5提高为0.63时,红蓝双方的兵力数量下降趋势基本重合。当蓝方获取信息的可靠性大于0.63时,蓝方兵力数量的下降速度慢于红方,蓝方在战斗结束时存在剩余兵力,而红方全部战损,图8是蓝方获取信息可靠性为0.75时的双方作战结果。
从上述实验分析可以看出,当蓝方决策的正确率从0.79提高为1时,红蓝双方的兵力数量变化曲线完全重合;当蓝方综合判断的准确度从0.8提高为1时,红蓝双方的兵力数量下降趋势基本重合;当蓝方获取信息的可靠性从0.5提高为0.63时,红蓝双方的兵力数量下降趋势基本重合;当蓝方获取信息的可靠性超过0.63时,蓝方作战效果优于红方。由此可知,在红蓝双方作战时,若红方在获取信息方面处于优势,则蓝方可以通过提高决策的正确率、综合判断的准确度或获取信息的可靠性来降低蓝方兵力的损耗,使双方的数量变化趋势基本一致,甚至使蓝方作战效果优于红方。
5 结论
通过构建红蓝双方对抗的系统动力学模型及仿真分析可知,红蓝双方除探测获取信息的速度这一变量外,在其他变量均相同的前提下,探测获取信息的速度对双方对抗的结果起决定作用,探测获取信息速度较快的一方,其兵力数量下降相对缓慢,另一方如果想要改变这种趋势,可以通过提高己方决策的正确率、综合判断的准确度或获取信息的可靠性来实现。提高至某一比例时,作战效果甚至优于对方。本文所构建的OODA作战环系统动力学模型并没有考虑外部环境因素的影响,下一步工作将会考虑社会、政治、经济、文化因素对作战兵力数量变化的影响,找出制约兵力数量变化的关键因素,为军事领域的决策者提供技术支撑。
