纵扭共振旋转超声加工系统设计

顾 磊,郑 侃,董 松

(南京理工大学 机械工程学院,江苏 南京 210094)

近年来,旋转超声加工技术在结构陶瓷、复合材料及高温合金等材料加工领域逐步得到了认可[1-3]。通过在刀具的轴向施加高频振动冲击,不仅可有效降低切削力,还可实现高精度低损伤加工。然而传统的旋转超声振动加工系统的振动方向是单一的纵振方向,在铣削加工时其主要铣削力方向与刀具振动方向存在差异,这样就极大地限制了超声加工的表现形式。而纵扭共振超声旋转系统具有更广泛的应用范围,相比于单一的普通旋转超声加工系统,其加工效率更高,切削力更小,加工表面质量更好。

Takuya[4]等设计了一种带斜槽的空心型阶梯变幅杆实现超声纵扭振动,并试验验证了该超声系统比传统纵振刀柄更有利于钻孔加工。文献[5]采用模式退化方法,利用波路径的几何修改将换能器中轴向极化压电陶瓷片激发的纵向响应转换为换能器前盖板中的纵扭振动。文献[6]利用切向极化压电陶瓷和轴向极化压电陶瓷组合来产生纵扭复合振动,并设计一种指数型变幅杆来放大纵扭超声换能器的振幅,但由于切向极化压电陶瓷造价昂贵,故没有得到广泛应用。唐军等[7,8]在分析纵扭超声加工机理的基础上,建立了分离纵扭复合超声铣削的动力学模型和稳定区域解析模型,并提出一种斜梁式纵扭超声加工系统。Chen T[9]等人设计了一种带有4个均匀斜槽的纵向扭转超声振动系统,采用有限元分析优化了振动系统的机械结构,对振动系统的动态特性进行了数值研究,分析了对角狭缝与共振频率和纵向扭转振幅的关系。

关于纵扭旋转超声加工设备的研究起步较晚,各国学者对纵扭复合超声波振动的各种转换结构(斜槽、斜梁)和叠加结构进行大量探索,并取得了一些理论研究成果。针对目前纵扭超声加工系统中存在的振动方向单一、加工难度大等问题,本文设计了一种小型化、轻量化纵扭共振旋转超声系统,通过在变幅杆上设计螺旋槽实现纵扭振动。研究表明该旋转超声加工系统可以较好地产生纵扭复合振动,适应多种加工环境。

1 纵扭超声系统结构设计

目前常用的两种超声换能器材料是夹心式压电换能器和磁致伸缩超声换能器,由于夹心式压电换能器具有结构简单、成本更低、能量转换效率更高等优点,本文选用夹心式压电换能器将激励源所产生的电压信号转化为纵向机械振动的能量形式,换能器谐振频率的设计值为30 kHz。

如图1所示,根据牛顿一维纵向振动传动原理的动力学方程[10],有

(1)

式中:S=S(x)为杆的任一横截面处的面积函数,ξ=ξ(x)为质点位移函数。

由于v=jωξ表示任意节面处波的振动速度,将式(1)变化为

(2)

当压电陶瓷组和后盖板为均匀的等截面杆,即S(x)=常数,式(2)可简化为

(3)

v(x)=Asinkx+Bcoskx

(4)

F(x)=-jZ(Acoskx-Bsinkx)

(5)

式中:F(x)为纵向弹性力;Z为各部分的声阻抗,Z=ρcS;A、B为待定系数。

如图1所示,将节面设置在压电陶瓷堆和前盖板之间,在节面左侧部分速度和力的边界为

v1(0)=vf

v1(l1)=v2(0)

v2(l2)=0

(6)

F1(l1)=F2(0)

F1(0)=0

(7)

式中:vf为后盖板左端的表面振速。将上列边界条件带入式(4)和(5),解得节面左侧频率方程

(8)

在节面右侧是一个圆柱形和指数形的复合杆,l3部分和l5部分根据式(3)和式(4)来确定,l4部分为指数变截面部分,假设大端的半径为R,小端的半径为r,则有函数关系

R=r·e-αx

S=S·e-αx

(9)

将式(9)带入式(2)中,可得任一指数型截面处质点的振速方程

(10)

对式(10)求解,可得指数型变幅杆任一质点处的通解

v(x)=eαx(Asink′x+Bcosk′x)

Beαx(αcosk′x-k′sink′x)]

(11)

节面右侧的边界条件为

v3(0)=0

v3(l3)=v4(0)

v4(l4)=v5(0)

v5(l5)=ve

(12)

F3(l3)=F4(0)

F4(l4)=F5(0)

F5(l5)=0

(13)

将式(12)、(13)带入式(4)、(5)、(11)中,解得节面右侧的频率方程

(k3-k5)αtank′4l4=k3k4+k4k5

(14)

由于压电陶瓷片的直径一般小于传递波长的1/4,因此有

(15)

2 纵扭共振超声系统有限元仿真

由于纵向振动波和扭向振动波在弹性体中的传播速度不同,导致同阶的纵振(Longitudinal vibration)与扭振(Torsional vibration)频率差异较大,因此本文考虑了纵振频率和扭振频率的差异性。而纵扭超声加工系统的谐振频率与系统的外形结构有直接关系,因此本文通过改变结构参数来改变谐振频率。螺旋槽式变幅杆不属于常规的变幅杆,传统的解析方法不适用于分析这种变幅杆,因此本文采用有限元分析方法来探讨螺旋槽对换能器的影响。

使用PROE建立纵扭共振超声系统三维模型,将换能器的三维模型另存为.xt文件,导入有限元分析软件WorkBench中,对换能器进行模态分析及动态响应分析。压电陶瓷材料选用SOLID226单元,金属材料选用SOLID187单元。设置材料参数如表1所示,运用自由网格模式进行网格划分,网格划分如图2所示。

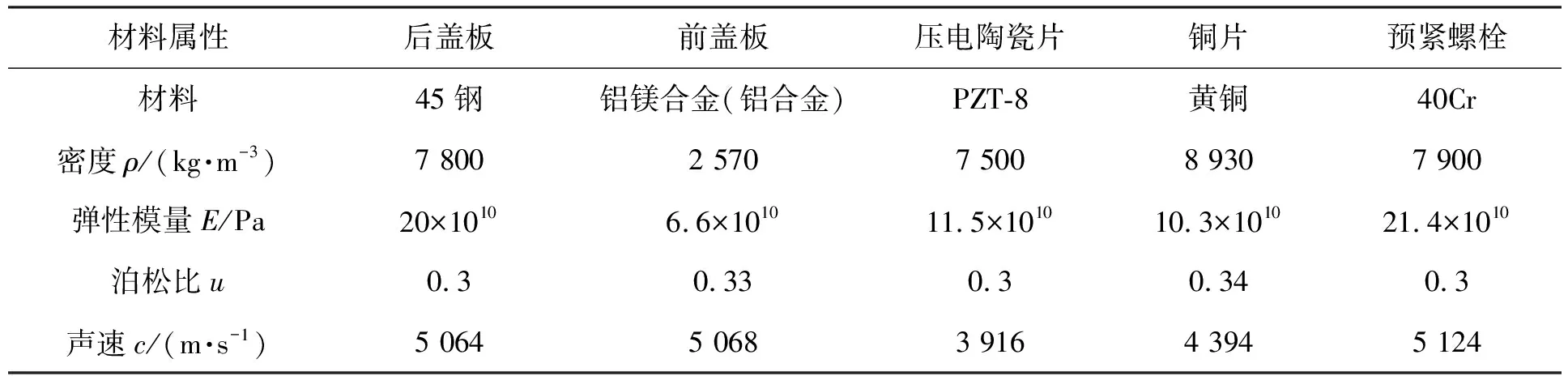
表1 材料基本属性

本文综合考虑螺旋槽的6个变化参数对纵扭振动的影响,受所采用结构的限制,各个参数只能在有限的范围内变化,由此确定实验方案。

螺旋槽切口形状的变化会导致谐振频率及扭振分量的不同,本文考虑矩形切割、梯形切割和1/4圆形切割3种不同的横截面,分析切口形状对变幅杆性能参数的影响。控制3种螺旋切口的面积基本一致,从而减小变幅杆的质量变化对谐振频率的影响。通过图3(a)可以发现,当切口的面积变化不大时,三者的谐振频率变化幅度微小,且三者纵振振幅的变化幅度小于1 μm,而1/4圆和矩形切口的扭振分量大于梯形切口的分量。考虑到加工难度及制作成本,选用矩形切口螺旋槽,以下分析皆以矩形螺旋槽为研究对象。

如图4(a)所示,在螺旋槽其他参数不变的情况下,纵振频率和扭振频率随着螺旋槽个数的增加而降低,两者的差值较为稳定。当螺旋槽数为5时,两谐振频率差值最小。随着螺旋槽数量的增加,系统的刚度随之减小,导致两者之间频率较为接近,此时由于变幅杆结构的限制,加工难度增大,且加工完成后的变幅杆存在应力集中问题。因此,须从扭振分量的角度来考虑螺旋槽数量问题,在其他条件一定的情况下,纵、扭振动振幅与螺旋槽数的关系如图4(b)所示。由图4可见,随着螺旋槽数量的增加,扭振振幅先增加后减少,当螺旋槽数为3时,扭振振幅达到最大,此时纵振振幅也较大,应力集中问题表现不突出,因此选择螺旋槽数为3。

螺旋槽数量确定后,需明确螺旋槽旋转角度与纵、扭谐振频率及振幅的关系。从图5(a)可以看出,随着螺旋角的增大,纵振频率逐渐减小,而扭振频率逐渐增大。在螺旋角达216°以后基本保持不变,两者的大小逐渐接近,螺旋角越大,频率简并的效果越明显。从图5(b)可以看出,当螺旋角逐渐增大时,扭振振幅先增大后减小,当螺旋角为288°时,扭振效果最好。综合考虑谐振频率及振幅大小,兼顾加工难度、加工成本及应力集中问题,选择螺旋角为288°。

从图6(a)可以看出,随着螺旋槽长度的增大,纵振频率和扭振频率的大小都逐渐减小,超过20 mm后,两个频率的差值相对稳定,约为1 000 Hz。而从图6(b)可以看出,随着螺旋长度的增大,纵振振幅先增大后减小,在20 mm处达到最大值并产生振幅突变。而扭振频率逐渐减小,超过20 mm后减小的趋势逐渐缓和,并趋于稳定。造成上述现象的原因是当螺旋槽长度达到20 mm时,纵振波的波峰位置处于螺旋槽位置,大部分传递的能量被螺旋槽吸收,从而导致振幅突变。综合考虑谐振频率及振幅大小,兼顾应力集中等问题,选择螺旋槽长度为20 mm。

比较图7可以发现,螺旋槽深度和宽度对于频率及纵振振幅的影响大致相同,随着槽深的增大,扭振振幅逐渐增大。由于螺旋槽深度的增大导致能量传递过程中滞留于沟槽中的能量更多,促使螺旋槽产生的扭振振幅更大;随着槽宽的增大,扭振振幅先增大后减小,槽宽增大后扭振振幅减小的可能原因是滞留于沟槽中的能量没有完全转化为扭振,由于沟槽宽度过大,导致能量更容易流失,造成更多的损耗。另外,过大的沟槽会导致变幅杆在加工过程中的刚性太弱,更容易引起加工颤振及加工误差,因此选择槽深为1.5 mm,槽宽为2 mm。

对最优参数下的纵扭超声系统进行模态分析及瞬态分析,设置压电陶瓷堆外界激励的幅值为250 V,分为40个子步。该系统的纵扭振动频率为30.723 kHz,图8为系统的总位移云图和位移矢量图。从图8看出,在系统末端产生明显的纵扭超声振动,而单一的纵向振动在经过螺旋槽时分解为纵振和扭振,可以看出位移矢量图末端的矢量有一定的角度,产生了两个方向的振动。仿真结果显示纵振振幅为11.7 μm,扭振振幅为5.1 μm。

3 纵扭共振超声系统振幅测量

3.1 实验设备

利用日本基恩士生产的OFV-525型激光测振仪对超声换能器的振幅进行测量,采用OFV-5000控制箱进行数据分析,并通过示波器解码控制箱输出的电压信号,分析振动波形及振幅大小。利用USP-G3超声电源给换能器提供电能,电源的工作频率为20～30 kHz。将各组件的线路连接好,并调整三脚架的位置及高度,将激光测振仪的激光对准纵扭超声刀柄的刀头,并在刀头上贴一层专用反光纸,聚焦后到控制箱的指示条信号达到稳定时开始测量。通过控制箱的数据采集卡采集信号,幅度为200 mm/(s·V-1)。利用示波器记录控制箱输出的电压信号,通过公式换算得到电压信号对应的超声振幅,每组实验测量3次,取其平均值。

3.2 实验结果

测量超声电流在0～100 mA变化时纵扭共振旋转超声系统所对应的纵振振幅和扭振振幅,超声电流在80mA时超声换能器纵向振动和扭振振动的电压信号如图9所示。由图9可见,由于控制箱输出的速度信号与位移信号的变化曲线具有一致性,可以看出电压信号为稳定规律的正弦曲线,即超声加工系统的振幅为稳定的正弦曲线,振幅大小通过式(16)求得,超声装置的纵振振幅为9.3 μm,扭振振幅为4.5 μm,实测结果与仿真结果误差小于10%。电压信号和刀柄振幅转换公式为

(16)

测量不同电流下纵扭共振超声刀柄的纵振振幅和扭振振幅,实验结果如图10所示。由图10可见,超声加工系统的纵振振幅和扭振振幅都随着超声电源电流的增大先增大后减小,并非单一的线性增大,在电流值为80 mA时振幅值最大,此时,纵振振幅为9.3 μm,扭振振幅为4.5 μm。超声刀柄的输出较为稳定,发热量较小,工作状态较为稳定。而随着功率的增大,换能器中的损耗及发热量提升,改变了压电陶瓷的性能,从而影响了换能器的输出振幅,最终导致刀柄的振幅减小。

4 结论

针对目前纵扭共振超声系统存在的扭振分量小、加工难度大等问题,本文设计了一种新型纵扭共振旋转超声加工系统,通过在变幅杆上开螺旋槽的方式来实现纵扭振动,研究表明该超声刀柄扭振分量较大,能够长时间稳定工作:

(1)根据一维动力学方程及振动传播理论,通过传统方法与有限元分析相结合的方式,分析了装置的结构参数对纵扭谐振频率和振幅的影响。由于螺旋槽的存在,纵扭复合振动在变幅杆中产生,因此纵扭振动特性取决于变幅杆的结构及螺旋槽的外形结构。螺旋槽的数量和长度在对谐振频率的影响中起主要作用,螺旋槽的深度和宽度主要影响纵波的传递与转换,而螺旋角主要影响纵振和扭振的耦合效果,并且螺旋槽各参数与频率和振幅的关系并不是单一的线性关系;

(2)运用激光振动测量仪对所设计的纵扭共振超声系统在不同电流下的纵向位移和扭转位移进行测量,采集了相关共振频率数据和振幅数据,进一步验证了结构设计的合理性。实验分析结果和仿真结果误差在10%以内,在谐振频率下,纵扭超声系统的纵振与扭振振幅均随超声电源功率增大先增大后减小,在电流值达到80 mA时振幅值最大。此时,纵振振幅为9.3 μm,扭振振幅为4.5 μm。而随着电流的增大,换能器中的损耗及发热量提升,改变了压电陶瓷的性能,从而影响了换能器的输出振幅。