基于量子粒子群与标准粒子群混合算法的框架结构异构体系模型参数辨识

张 迁,丁建国

(南京理工大学 理学院,江苏 南京 210094)

由于框架结构空间分隔灵敏,自重轻,同时能够节约材料,在选用现浇混凝构造的特色土构造框架结构时,结构的整体性和刚度较好,同时也能达到较好的抗震作用,因此,框架结构在实际工程中的应用很多。目前,对于框架结构异构体系模型简化的相关研究较少,而采用多体系统传递矩阵法研究地震碰撞的模型简化更少,本文提出了一种简化框架结构异构体系的方法,模型中的各个参数通过参数识别的方法来确定。

目前,识别参数的方法主要有遗传算法、蚁群算法、神经网络算法、微分进化算法、粒子群算法等,但是单独的参数识别方法往往识别精度不高,收敛速度较慢,所以现在关于改进参数识别方法的研究较多,改进的途径主要有两种:一是利用其他优化技术自适应调整算法的相关参数;二是将两种或者多种优化算法进行结合。李世光等[1]在基本的量子粒子群算法基础上引入微分进化算子来保证种群选择的多样性,提高全局搜索能力,并且引入混沌扰动来加快算法后期收敛速度,从而提高搜索精度,并将该方法应用于解决大型船舶配电网的故障问题;谢源等[2]利用柯西变异能快速跳出局部极小值的优点,将量子粒子群算法的收缩扩张因子进行改进,并将改进的算法应用于变差函数球状模型的拟合;李盼池等[3]分别基于Delta势阱、谐振子和方势阱提出了改进的量子势阱粒子群优化算法,并提出了基于统计量均值的控制参数设计方法;徐珊珊等[4]在惯性权重自适应调整的量子粒子群优化算法基础上,提出了带全局判据的改进量子粒子群优化算法。郭蕴华等[5]在标准量子粒子群算法的基础上,加入动态修正粒子更新位置的方法,从而使算法的寻优能力加强,收敛速度加快,并且将该算法应用于无人机路径规划问题;彭广等[6]在粒子群算法中引入动态量子旋转门,并且采用相位角进行实数编码方法,改进了量子粒子群算法的性能,并通过两个测试函数测试了该方法的寻优性能。陈功贵等[7]对标准量子粒子群算法的收缩扩张系数采用指数下降型修正,从而提高了算法的局部搜索能力和全局搜索能力;黄丽等[8]采用正弦混沌序列提高初始化粒子位置的遍历性及种群多样性,并结合模拟退火算法能跳出局部最优的特点来增强量子粒子群寻找全局最优能力,提出一种改进的量子粒子群算法;胡皞等[9]在标准量子粒子群算法中引入同化和竞争思想,该改进算法将民族间的同化竞争思想引入粒子寻优过程,以全局最优粒子作为中心粒子,不断同化其余粒子,使粒子之间保持不断竞争关系,以改进粒子的进化方式,提高粒子的寻优性能,并将改进算法应用于结构模态参数识别,采用简支梁数值模型对该算法的有效性进行验证;李建平等[10]改进了量子粒子群算法,该算法中初始化种群采用Beta分布,惯性权重更新采用逆不完全伽马函数,并将基于差分进化的新算子引入到速度更新式中,对粒子进行越界处理,以50个不同类型的数值函数作为优化实例进行验证;冯仲恺等[11]通过混沌搜索增强初始种群质量,在更新种群最优位置中心时进行加权,使种群的进化模式得到改善,从而使算法的收敛速度得到提升;赵莉[12]在量子粒子群算法中,为了防止早熟现象的出现,引入随机序列对粒子的平均最优位置进行扰动,从而使粒子的多样性增加,避免算法陷入局部最优解,提升了算法的寻优能力。

粒子群算法(PSO)是一种新型的仿生算法,由Kennedy和Eberhart于1995年提出,该算法是基于群体的智能算法,其功能与遗传算法非常相似,粒子群算法因为调节的参数少,并且简单易于实现,越来越多地应用于函数优化、神经网络训练、模式分类以及其他领域。

由于粒子群优化算法不是一个全局收敛算法,并且全局搜索能力对速度上限的过度依靠降低了粒子群优化算法的鲁棒性,同时参数选择有一定困难,所以孙俊等提出了具有量子行为的粒子群优化算法(QPSO),并且证实了该方法在寻优能力和收敛速度上都优于标准的粒子群优化算法。

由于标准粒子群算法和量子粒子群算法的识别精度不高,并且两种算法的收敛速度也不快,所以本文基于标准量子粒子群算法提出了一种将量子粒子群与标准粒子群混合的参数辨识算法,并将其应用于框架结构异构体系模型的参数辨识。

1 力学模型的建立

通常一个实际的物理模型会对应多个力学模型,本文为了方便多体系统传递矩阵法(MS-TMM)计算相邻结构的地震碰撞问题,将一个多层的框架结构简化为一个树形拓扑动力学模型,既将每层的所有梁柱以及楼板简化为一个集中质量,将每层的所有柱简化为若干个集中质量和无质量弹性梁,简化的力学模型如图1所示。

2 参数辨识

在进行MS-TMM地震碰撞计算时,传递矩阵的相关参数无法确定,所以将框架结构通过Ansys进行建模,通过模态分析求出该框架的前若干阶频率,从前n阶频率中挑选出m阶与简化力学模型相同的频率。

令目标函数

(1)

式中:wk为Ansys计算的频率,w′k为多体系统传递矩阵法(MS-TMM)计算的频率。

通过参数识别的方法求出目标函数的最小值,此时对应的EI(抗弯刚度)参数即为识别结果。

2.1 量子粒子群算法(QPSO)

关于QPSO的进化方程为,如果粒子在以点P为中心的一维δ势阱中运动,采用蒙特卡罗法得出粒子的位置方程为

(2)

式中:μ=U(0,1),L为δ势阱特征长度,随时间变化。

经推导,粒子更新方程为

(3)

pid=φpij+(1-φ)Gj

(4)

(5)

式(2)-(5)中:m为粒子数,n为维数,φ～U(0,1),pij为由个体经验知识确定的最优值,Gj为由群体知识确定的群体最优值。α为收缩扩张系数,其计算式为

(6)

式中:α1和α2分别为α的初始值和终止值,t为迭代次数,Imax为最大迭代次数。

QPSO算法计算流程如图2所示。

2.2 自适应粒子群算法

自适应粒子群优化(APSO)算法在PSO算法的基础上对惯性权重系数进行了改进,使该算法在收敛速度和稳定性上均得到了提升,其数学描述为

(7)

(8)

(9)

式中:k为当前迭代次数,ωmax为权重最大值,取0.9,ωmin为权重最小值,取0.4,Imax为最大迭代次数。

APSO算法的计算流程如图3所示。

2.3 量子粒子群与标准粒子群混合算法

为了提高量子粒子群算法的收敛速度和寻优精度,本文提出了一种量子粒子群与标准粒子群相结合的混合算法。由于标准的量子粒子群算法只有收缩扩张系数α一个控制参数,本文在PSO算法的基础上加入了惯性权重系数ω和学习因子c1,c2,从而提高了算法的收敛速度和计算精度。其数学描述为

(10)

(11)

(12)

式中:α1取1.0,α2取0.5。c1,c2为学习引子,其计算公式为

(13)

式中:ω为惯性权重系数,定义为

(14)

式中:k为当前迭代次数,ωmax为权重最大值,取0.9;ωmin为权重最小值,取0.4;Imax为最大迭代次数。量子粒子群与标准粒子群混合算法的计算流程见图4。

3 多体系统传递矩阵法基本原理

3.1 典型原件的传递矩阵

3.1.1 一端输入一端输出集中质量

根据文献[13],一端输入一端输出集中质量的受力情况如图5所示,其中质量为m,输入端为I,输出端为O。

集中质量的输入端和输出端的状态矢量在物理坐标下可以表示为

(15)

根据集中质量的特点可得

(16)

由受力关系可得

(17)

输入、输出端的状态矢量在模态坐标下为

(18)

根据物理坐标和模态坐标的关系有

(19)

其中系统的固有频率为ω。

集中质量单元的传递方程为ZO=UZI,根据式(16)、(17)、(19)可得一端输入一端输出集中质量的传递矩阵为

(20)

3.1.2 纵向无质量弹性梁

根据文献[13],纵向无质量弹性梁的受力情况如图6所示,弹性梁的长度和抗弯刚度分别为l和EI,弹性梁的输入端和输出端分别为I,O。

输入、输出端在物理坐标下的状态矢量为

(21)

由受力平衡可得

(22)

以弹性梁输入端I为坐标原点,建立坐标系,不考虑弹性梁轴线方向的变形,则其输出端O的转角和横向位移分别为

(23)

根据式(22)、(23)可得输出端和输入端的变形关系为

(24)

该单元的传递方程为ZO=UZI,根据式(22)、(23)、(24)以及单元的物理坐标和模态坐标之间的关系,可得纵向无质量弹性梁的传递矩阵为

(25)

3.2 总传递矩阵与传递方程

系统总传递矩阵与传递方程为

Uall=Un×Un-1×Un-2×…×U3×U2×U1

(26)

计算结构频率时根据图7所示的计算流程,并采用Matlab语言编制程序。

4 工程算例

本算例引用文献[17]中的试验模型,为三层钢筋混凝土框架结构,整体尺寸为 1 000 mm×1 000 mm×2 400 mm,梁、柱截面尺寸为70 mm×70 mm,板厚为70 mm,混凝土密度ρ=2 450 kg/m3,泊松比为0.2,弹性模量为30 GPa。

在Ansys数值模拟[18]中,使用beam188单元来模拟梁柱单元,使用shell181单元模拟楼板单元,在划分网格时,所有的梁和柱都取5个单元,每一层楼板取25个单元,整个模型beam188单元共60个,shell181单元共75个。所建Ansys模型如图8所示。

在简化为树形拓扑动力学模型时,将每层的4根柱简化为4个质量相等的集中质量m1=43.904/4 kg和5根长度相等的无质量弹性梁,将每层的所有梁和楼板简化为一个集中质量m2=219.52 kg,简化的力学模型如图9所示。

通过多体系统传递矩阵法的相关内容求解结构的固有频率,其中传递矩阵中抗弯刚度EI为待识别参数,共有15个待识别参数,因为简化之后的模型主要考虑x方向的振动,所以从Ansys计算结果的前100阶模态中选取4阶(第1,第7,第51,第65阶)x方向的振动作为识别标准(振型见图10),分别通过量子粒子群算法、自适应粒子群算法和量子粒子群与标准粒子群混合算法来识别参数。在进行参数辨识时,3种方法选取的迭代次数均为10 000次,并且经过多次不同种群规模数量验证,选择种群规模为300,为了保证实验结果的可靠性,两种方法都进行10次实验,并将10次实验的结果取平均值。3种方法的适应度变化情况如图11所示,3种算法的参数识别结果见表1。

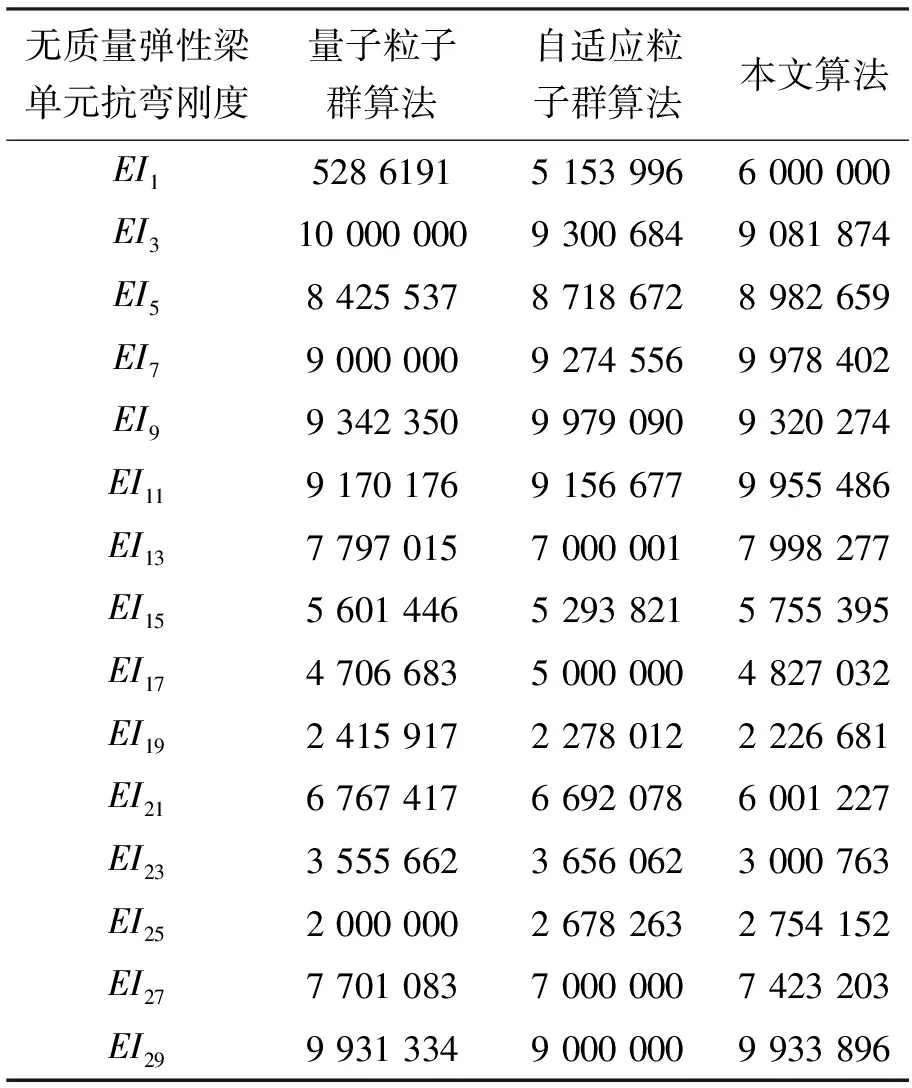
表1 3种算法参数识别结果

为了验证识别结果的可靠性,将参数识别的结果利用MS-TMM相关方法计算结构的自振频率,并与Ansys计算结果进行比较,结果见表2。

表2 自振频率计算结果误差分析结果

从识别结果可以看出,对于1、2阶频率来说,量子粒子群与标准粒子群混合算法的识别精度更高,而对于3、4阶频率,量子粒子群算法的识别精度更高,但是由于低阶频率对于动力学模型力学参数的影响更大,且对于前两阶频率来说,Ansys模型的变形和所转化的树形拓扑动力学模型的变形更加相似,因此,本文提出的量子粒子群与标准粒子群混合算法对辨识框架结构树形拓扑动力学模型力学参数的辨识效果更好。

5 结论

(1)基于多体系统传递矩阵法建立了框架结构的树形拓扑动力学模型,并推导了模型中相关元件的传递矩阵、整个系统的总传递矩阵和总传递方程。

(2)在量子粒子群算法的基础上,引入标准粒子群算法的惯性权重系数和学习因子两个控制参数,提出了一种将量子粒子群和标准粒子群混合的参数辨识方法,并将此方法应用于框架结构树形拓扑动力学模型相关力学参数的辨识。

(3)本文提出的量子粒子群与标准粒子群混合的参数辨识方法在进行框架结构树形拓扑动力学模型力学参数辨识时,前两阶频率的误差分别为6.3%和0.1%,明显低于其他两种方法,因此,相对于普通的量子粒子群算法和自适应粒子群算法,本文算法识别精度更高。