血管造影锥形束CT重建算法中的滤波器设计研究*

冯聪聪 宣 晓* 高 上 黄 岩 申 杰 王东海

目前，锥形束计算机断层摄影(cone-beam computed tomography，CBCT)成像技术已被广泛应用于医疗诊断和治疗过程中，在血管介入治疗领域，神经血管的CBCT成像对诊断和治疗具有重要意义，尤其是在颅内动脉瘤、颅内血管畸形、血管狭窄、颅内出血、颅内血管内支架成形术等脑血管疾病手术中[1]。由于普通的二维X光成像在物体深度方向为重叠，不利于显示血管间、血管和组织间的相对关系，而CBCT生成的三维血管图像可以全面显示不同血管和组织结构间的相对位置关系，可根据感兴趣的病变位置，按任意角度旋转图像进行观察，找到最佳治疗位置。在三维图像上可对血管瘤大小、血管最窄及最宽直径等指标进行测量，而二维图像只有一个投影面，测量结果不全面。此外，如果有弹簧圈或者支架等植入，还可以在三维图像中观察植入物和血管的相对位置，便于分析治疗效果[2]。三维血管图像的质量直接影响医生的诊断和治疗，如果血管模糊、边缘显示不清，不仅不利于观察，还可能会对测量精度产生影响。目前，无论是普通CT还是CBCT，三维重建大都采用的是FDK(由Feldkamp-Davis-Kress名字命名)三维图像重建算法(FDK算法)[3-4]。FDK算法具有成熟和速度快的优点，重建效果好，其基本原理为：①对二维投影数据进行加权，适当地修正体素到源点的距离和角度差；②对不同投影角度的加权投影数据进行水平方向的一维滤波；③沿X射线方向进行加权反投影重构。

1 FDK算法与滤波函数

FDK算法关键步骤是滤波，常见的滤波器有汉明滤波器(Hamming)、斜坡滤波器(Ram-Lak)及谢普·洛根滤波器(Shepp-Logan)等[5-7]。这些滤波器如果直接使用，算法得到的血管束主干血管是可见的，但都会有各自的问题。如血管边缘不够清晰光滑，周边有毛刺伪影，细小分支显示较模糊等，影响医生对血管畸形、狭窄等情况的判断和测量。为此，本研究对FDK重建算法的滤波部分进行设计，优化滤波函数，除添加平滑与截止滤波函数外，设计了一种新的高频增强滤波函数，用这种组合滤波器的方式起到增强血管，消除周边伪影的作用，进而提升三维血管图像质量。

1.1 标准滤波函数

使用Shepp-Logan滤波器作为标准滤波函数，其时域滤波函数[8-9]计算为公式1：

1.2 平滑滤波函数

由于三维血管图像以显示血管形态为主，要求血管边缘光滑无毛刺，因此本研究设计了一个基于高斯函数的平滑滤波函数，在Shepp-Logan标准滤波函数基础上乘以平滑滤波函数，可以平滑血管，减小噪声，其频域平滑滤波函数计算为公式3：

式中S为可调节参数，典型值为S=2，x∈(0，N-1)，N为探测器宽度的像素数。

当重建矩阵的体素尺寸大于探测器像素尺寸时，意味着重建体的分辨率低于探测器的原始图像，则重建图像无法将高频信息进行完全表示，可能会出现高频混叠伪影，而且噪声会增加，因此需要进行额外的滤波来截断高频。定义M=N×sizeprojectedpixel/sizevoxel，其中，sizeprojectedpixel是探测器像素尺寸，sizevoxel是重建体素尺寸。

当x∈(0，M-1)时，其频域截止滤波函数计算为公式4：

否则为公式5：

由于Shepp-Logan公式是时域滤波函数公式，需要进行快速傅里叶变换(fast Fourier transform，FFT)至频域，再与其他滤波函数相乘，最后进行逆变换，结果记为基本滤波函数，所以三维重建所需的基本滤波函数计算为公式6：

1.3 高频增强滤波函数

经过标准滤波函数和平滑滤波函数组成的基本滤波函数，图像的噪声已经被抑制，血管得到了平滑。但是，血管本身的对比度，以及血管边缘的锐利程度还需要提高。为了增强断层图像中血管的显示，在上述基础上又设计了指数型高频增强滤波器。

否则滤波函数计算为公式8：

式中power1和boost1为增强参数，设置参数的目的是使滤波器更灵活，可以通过改变参数自行去设计高频滤波的程度，达到想要的滤波效果。典型值如boost1=1，power1=6，此时高频滤波函数在频域的曲线见图1。

图1 高频滤波指数型函数曲线

如果boost1=0，此时的滤波函数实际上是一个常数1，不起到增强作用。如果boost1＞0，则可以对高频成分进行增强，power1可以控制增强的频率范围。

为了达到最优的效果，在公式(7)和(8)基础上仍可以继续叠加指数型滤波函数，改变参数实现对不同频段的增强。具体为：定义，当，即时，其滤波函数计算满足公式9：

否则滤波函数计算为公式10：

式中boost2和power2为增强参数，典型值如boost2=2，power2=10。

从滤波函数公式上可以看出，根据需要滤波器可分开使用，也可以组合在一起，通过调节参数，达到更为灵活的调节效果。两个指数型滤波器叠加在一起与单独滤波器对比曲线见图2。

图2 高频滤波函数对比曲线

在基本滤波函数基础上加入高频增强滤波器后的滤波函数记为F′，其计算为公式11：

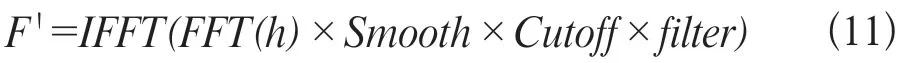
式中filter为最终的高频增强滤波函数。

为了更好的表明高频增强函数的作用，基本滤波函数与加入高频增强滤波函数进行比较，图像的中高频部分得到了增强。通过调节参数，应使增强部分恰好对应血管信号的频率域，能够实现有针对性的血管增强。基本滤波函数和加入高频增强滤波函数比较见图3。

图3 基本滤波函数和加入高频增强滤波函数比较

标准滤波函数、平滑滤波函数和高频增强滤波函数均为一维滤波，本研究是对二维图像进行处理，因此在探测器高度方向同样需要进行上述滤波函数计算，其方法相同。

2 研究资料与方法

2.1 研究资料

使用东软医疗血管机NeuAngio 30C在山东大学齐鲁医院进行了50例脑血管三维旋转造影，采集到的原始数据自动传输至后处理工作站自动进行三维重建，得到断层图像，工作站界面会自动显示三维血管图像，验证CBCT在重建三维血管图像算法中的滤波器设计的可行性和临床意义。

2.2 研究方法

选取4组具有代表性的患者数据，分别使用基本滤波函数和加入高频增强滤波器的滤波函数进行三维重建，并对基本滤波函数与高频增强滤波函数重建结果进行比较。

3 结果

3.1 两种滤波函数断层图像比较

使用基本滤波函数进行三维重建，得到的断层图像结果与在基本滤波函数基础上加入高频增强滤波器的断层图像结果的比较显示，高频增强滤波函数断层图像中血管部分与背景的对比度更强，边缘更锐利[10]。两种滤波函数断层图像比较见图4。

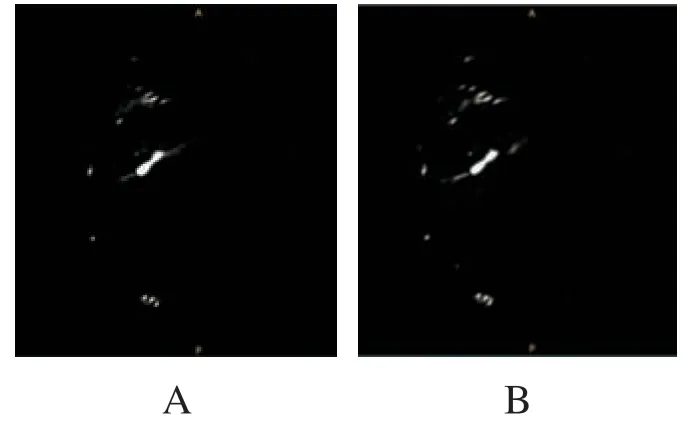
图4 两种滤波函数断层图像比较

3.2 两种滤波函数三维血管图像比较

使用基本滤波函数进行三维重建得到的三维血管图像，与在基本滤波函数基础上加入高频增强滤波器进行三维重建得到的三维血管图像进行比较，其结果见图5。

图5 两种滤波函数三维图像比较

3.3 两种滤波函数三维放大血管图像比较

在后处理工作站放大三维血管束，从细节对比滤波器改进前后血管质量的变化。使用基本滤波函数进行三维重建得到的三维血管放大结果与在基本滤波函数基础上加入高频增强滤波器进行三维重建得到的三维血管放大图像进行比较，其结果见图6。

图6 两种滤波函数三维放大血管图像比较

3.4 滤波器改进前后不同角度下血管变化比较

旋转三维血管束，从不同角度对比滤波器改进前后血管发生的变化，加入高频增强滤波器进行三维重建得到的三维血管束效果有明显的改善，可以显示更多的血管，细小分支显示清晰，血管边缘光滑锐利、管壁连续完整。滤波器改进前后不同角度下血管变化比较见图7。

图7 滤波器改进前后不同角度下血管变化比较

4 结论

本研究提出的一种新的组合滤波函数，主要方法是在标准Shepp-Logan滤波函数基础上，加入平滑滤波和高频增强滤波器，能够有效地消除血管图像周边伪影，增强血管边缘，得到更高图像质量的三维血管图像。临床患者试验结果证实，加入平滑滤波和高频增强滤波器组合能够起到增强血管的作用，提高断层图像的质量，使三维血管渲染效果更好，有助于临床诊断与治疗，具有重要的临床意义。