基于ECC与同态加密的加密算法
2020-05-22郎显赫裴少婧
刘 艳,郎显赫+,裴少婧
(1.大连大学 辽宁省北斗高精度位置服务技术工程实验室,辽宁 大连 116622;2.大连大学 大连市环境感知与智能控制重点实验室,辽宁 大连 116622;3.中原工学院 机电学院,河南 郑州 450007)
0 引 言
随着互联网与云计算的发展,人们在私人信息搜索、移动代码与电子投票等方面的需求日益增加,同态加密[1]变得更加重要。Rivest等提出RSA加密方案,利用同态加密的性质进行对数据进行加密,之后同态加密技术得到了进一步发展,取得了一些代表性的研究成果,彭长根等[2]基于同态加密提出一种可传递的签名方案,利用同态加密的密文可运算特性实现了可传递签名及验签的通用模型。杨玉龙等[3]提出防止SQL注入攻击的同态加密解决方案,段淑敏等[4]提出基于RSA代理重加密的同态加密方案,杨攀等[5]提出支持密文四则运算的CESIL同态加密方案。但是这些传统的同态加密方法存在公钥尺寸过大,计算复杂度高,运算效率低等缺点,不能实际应用于云中,本文针对这一问题,提出一种基于ECC与同态加密技术的加密方案,该方案具有高效的运算效率和高安全强度。
1 同态加密技术
同态加密允许服务器在不知道原始明文的情况下做加密数据的操作,允许对加密后的数据执行特定的数学运算并且解密结果和对应明文进行运算后的结果是一致的,从而保护了数据[6]。数据加密解密基本流程如图1所示。
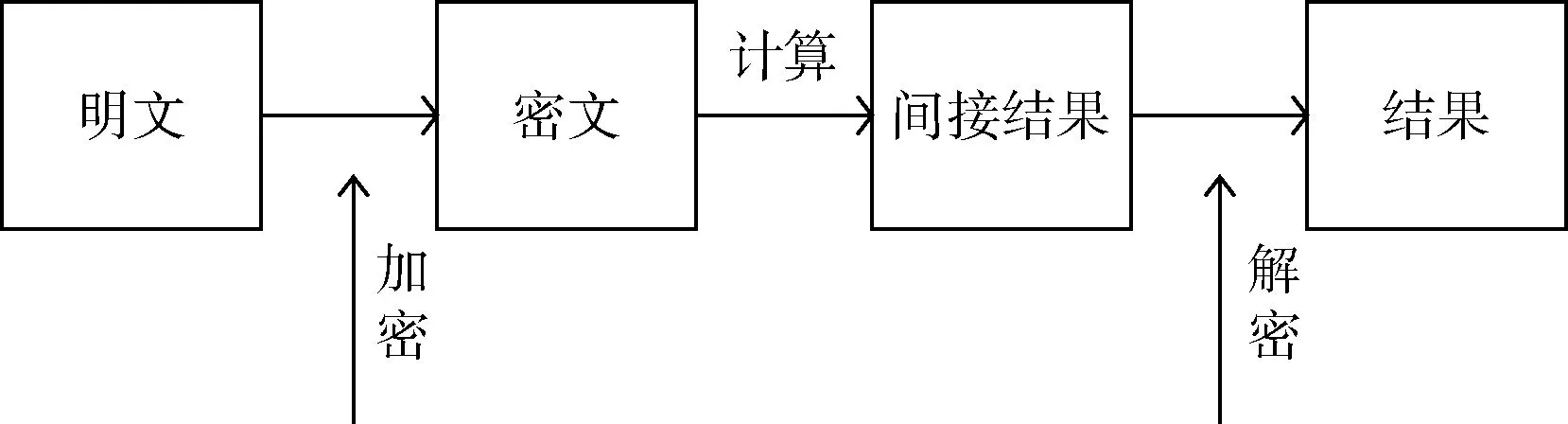
图1 数据加密解密基本流程
假设一个加密系统中加密算法为CK,解密算法为DK,明文为n、m,则同态加密满足如下属性
DK(CK(n)*CK(m))=n*m
(1)
DK(CK(n)+CK(m))=n+m
(2)
上述加密方法第一个属性是乘法同态加密,第二个属性是加法同态加密,如果两个属性同属满足,则加密算法成为完全同态加密[7]。由于加法同态加密运算较少,相对于乘法可忽略不计,所以本文仅研究乘法同态加密,为后续进一步密文检索技术的研究提供技术支撑。
2 椭圆曲线加密技术
椭圆曲线并不是椭圆,之所以称为椭圆曲线加密是因为它的曲线方程与计算椭圆周长的方程相似。一般椭圆曲线指的是维尔斯特拉斯(Weierstrass)方程所确定的椭圆曲线,形如:y2+axy+by=x3+cx2+dx+e,它是由方程全部解(x,y)加上一个无穷远点O构成的一个集合。椭圆曲线加密算法的安全性建立在求椭圆曲线离散对数解困难性(ECDLP)[8]之上,设曲线E及曲线上的两点G和Q,其中Q=xG,求x就是椭圆曲线的离散对数问题[9]。
设基础域F,x,y属于F且满足如下:
y2+axy+by=x3+cx2+dx+e,通过坐标变换转换为下述形式
E∶y2=x3+ax+b
式中:a、b、x、y属于有限域Fp,其中p是一个大于3的大质数。假设曲线上的两点P(x1,y1),Q(x2,y2),连接它们的直线L的斜率Δ=(y2-y1)/(x2-x1)。L恰与椭圆曲线相交于另一点R(x3,y3),则R为Q与P之和的负元,即P+Q=-R。 其中
x3=Δ2-x1-x2
(3)
y3=-x1+Δ(x1-x3)
(4)
点加几何表示如图2所示。
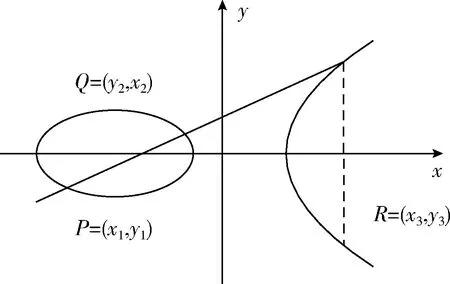
图2 点加几何表示
为计算点P的两倍,过P点画一条切线并找出另一交点S(x3,y3),则P+P=2P=-S,其中
(5)
(6)
椭圆曲线加密技术是一个很有前途的加密体制,加密时需将明文嵌入椭圆曲线上的随机一点,解密时需要把椭圆曲线上的点解码为明文信息,加密解密用公钥Q和私钥k进行[10]。椭圆曲线加密过程如图3所示。
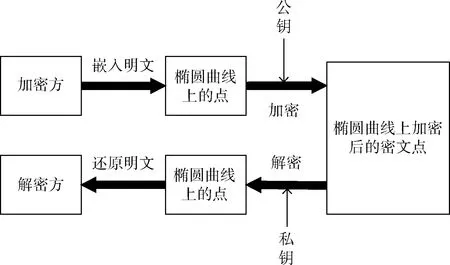
图3 椭圆曲线加密过程
3 基于ECC的同态加密改进算法
本文提出的改进同态加密算法,兼顾了ECC的低运算复杂度、高安全性与同态加密的密文可操作性。通常加密数据用时仅几秒甚至几毫秒,可密钥存储在云端会几年甚至几十年,攻击者拿到密文后有足够的时间来破解。为此,为了加强数据的传输及存储安全性,本文使用不同的私钥k对明文进行加密,旨在提高基于ECC的同态加密算法的安全性。
设用户A将上传并存储明文 (M1,M2,…,Mn) 到云端,加解密过程如下:
(1)用户A在本地生成椭圆曲线E及曲线上随机基点G,同时选择不同的私钥 (k1,k2,…,kn) 生成公钥加密明文以加强整体数据的安全性;
(2)用户A将基点G与私钥 (k1,k2,…,kn) 进行标量乘运算生成公钥 (Q1,Q2,…,Qn),其中Qi=G·ki,客户端保存私钥 (k1,k2,…,kn) 到本地;
(3)为了对明文 (M1,M2,…,Mn) 进行加密操作,用户A要将明文嵌入到选好的椭圆曲线E中,得到明文点 (Pm1,Pm2,…,Pmn);
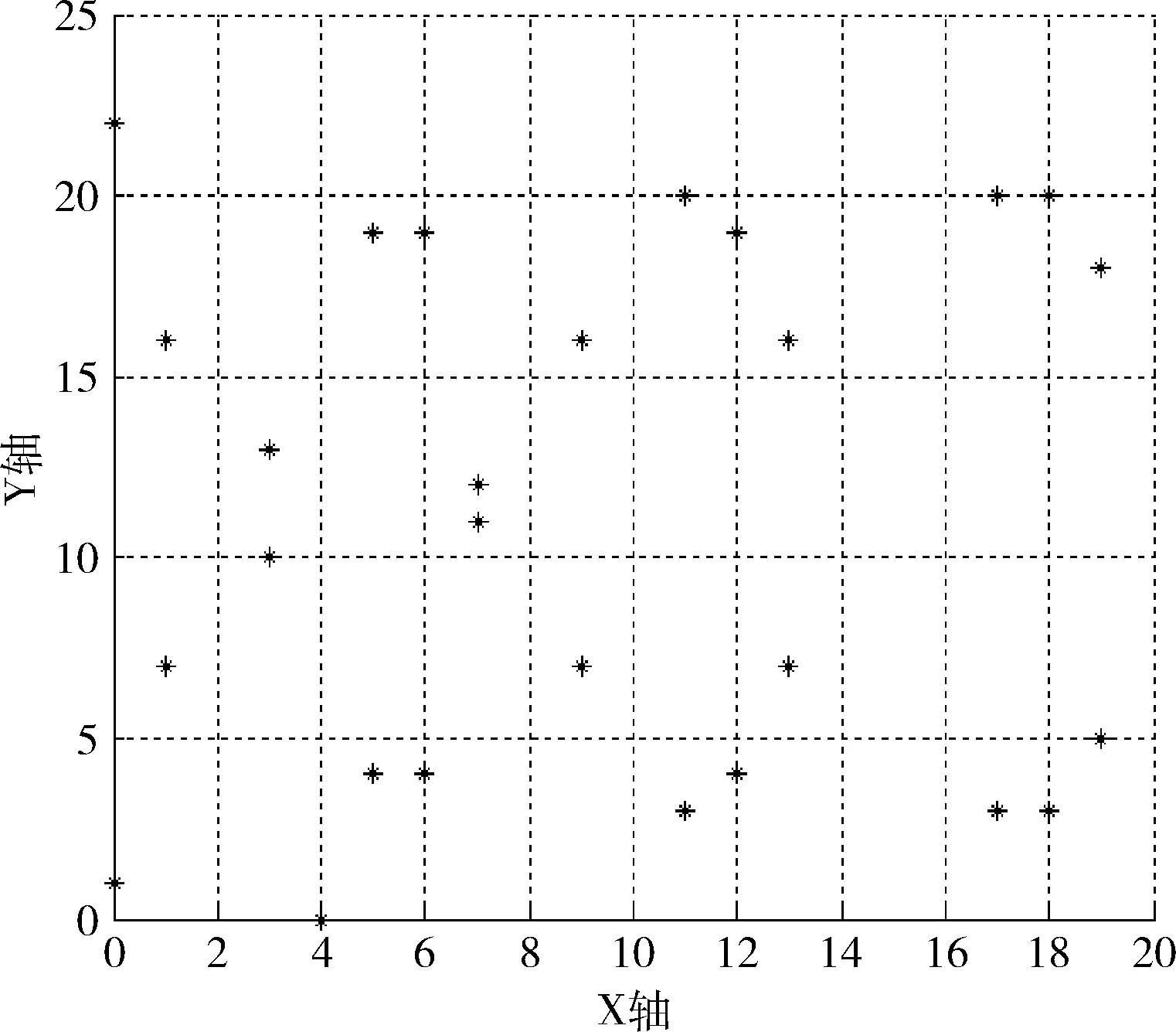
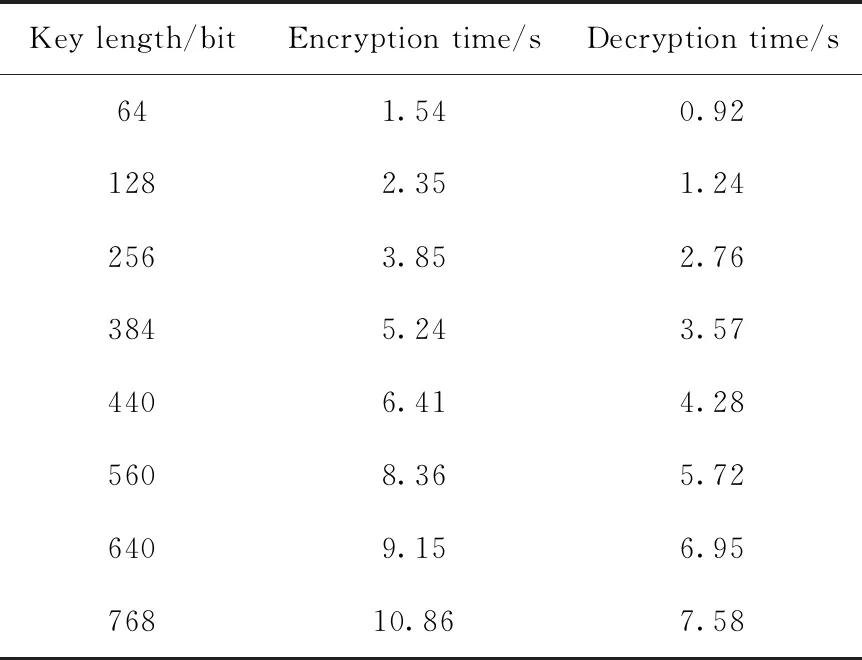
(4)用户A随机生成整数 (r1,r2,…,rn),其中随机数r C1i=ri·G (7) C2i=C3i·Pmi (8) C3i=ri·Qi (9) 加密后的密文为 C1(C11,C21)…Cn(C1n,C2n) (10) (11) (6)用户A利用本地存储的私钥 (k1,k2,…,kn) 解密 (12) 则 (13) 云端只接收了加密后的密文,无其它可用数据,从而防止了私密消息在云端内部的泄露,同时使用不同的私钥k对明文加密,极大地加强了安全强度。因此,本文算法既有椭圆曲线加密技术算法的高计算效率、高安全强度,也有同态性。 为了对本文算法的计算性能进行测试,本文采用i5处理器、8GRAM,并使用JDK1.8模拟客户端对用户的私密信息进行加解密,并将密文传输到腾讯云平台中。 ECC的安全性取决于椭圆曲线群上离散对数的求解,而椭圆曲线离散对数求解的困难性远大于分解大素数的困难性,所以基于椭圆曲线加密技术的同态加密相对于RSA同态加密有着更高的安全性。例如曲线y2=x3+x+1,P=23,其散射点分布如图4所示,包括无穷远点在内的散射点多达28个,呈现了较强的无序性与离散性。实际工程应用多达200个点以上[11],所以文中所提的加密算法足以保证实际应用加密算法的有效性。 图4 椭圆曲线散点 相对于一般加密方式,使用同态加密可以在密文上直接运算,即保证了数据安全和数据隐私,又提高了密文传输速率。由于椭圆曲线加密技术的密钥尺寸和系统参数相对于RSA,DSA要小很多,所以ECC所占存储空间要小很多[12]。椭圆曲线加密技术的安全强度相对于RSA,DSA有非常明显的优势,由表1可知,160位密钥的椭圆曲线加密技术算法安全强度就相当于1024位密钥的RSA/DSA算法安全强度,有效地解决了因提高安全强度而增加密钥长度所带来的工程实现难的问题。使用不同的私钥k对明文加密的方式,使该方法的安全性在椭圆曲线加密技术的安全性基础上又有了极大的提高。所以基于ECC的同态加密方法相对于RSA/DSA同态加密方法有更高的安全性和加密性能。 表1 相同安全等级ECC/RSA/DSA所需密钥长度 为了满足实际工程的安全需求,实验采用256 bit的有限域P,同时使用不同长度的密钥对明文进行加密解密时间见表2。 表2 加密/解密时间 基于椭圆曲线加密技术同态加密方法的加密解密部分基于ECC,明文密文运算基于同态加密,由表1、表2易见随着密钥长度的增加,基于椭圆曲线加密技术同态加密方法节约空间的优势明显,并且随着加密强度的提高,该加密方法密钥长度变化不大,因而基于椭圆曲线加密技术的同态加密方法密钥短的优点是非常明显的。本文算法和RSA同态加密算法加解密相同明文的平均时间见表3,本文算法的加解密效率相对RSA同态加密算法具有明显的优势,RSA加密算法由于受到素数产生技术的限制,导致密钥产生很麻烦,因此RSA同态加密的运算效率很低[13]。而本文中使用不同长度的密钥对本文中的方法进行实验,加密解密效率理想。 表3 本文算法与RSA算法运算100次平均时间 随着云计算与大数据的迅速发展,安全问题成为了急需解决的问题。本文结合椭圆曲线加密技术与同态加密技术,提出了一种改进的同态加密方法,该方法既有椭圆曲线加密技术算法的高计算效率、短密钥、高安全强度,也有同态加密的密文可操作特性。使用不同的私钥k对数据加密,解决了一个私钥被破解,全部数据都泄露的问题,从而极大地提高了基于椭圆曲线加密技术的同态加密的安全性。
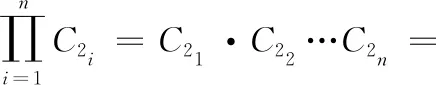
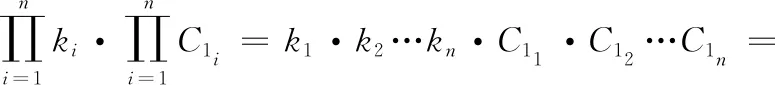
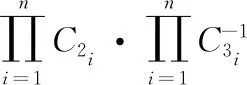
4 实验结果与分析
4.1 安全性分析

4.2 计算性能分析

5 结束语
