基于快速响应码的非线性光学图像加密算法
2020-05-22张文惠丁世飞谭云兰
张文惠,丁世飞,谭云兰
(1.中国矿业大学 计算机科学与技术学院,江苏 徐州 221116;2.徐州幼儿师范高等专科学校信息网络中心,江苏 徐州 221004;3.井冈山大学 电子与信息工程学院,江西 吉安 343009)
0 引 言
如何确保图像在网络中安全传输已是学者的关注热点[1-3]。在已有的数据安全技术中,较为流行的方案包括混沌加密[4-7]与光学加密[8-10]。
混沌加密系方案是依赖其较高的不可预测性等优点来改变像素位置与像素值,如王瑶等[4]利用混合混沌系统所输出混沌序列来改变像素在明文的位置,同时,建立多方向连续扩散机制,利用不同方向对应的加密函数来改变像素值。Musheer等[5]利用粒子群优化来构建图像加密方法,借助粒子群算法获得优化的加密效果,利用明文内容来生成Logistic映射的初始条件,根据式输出的随机序列来构建加密函数,实现明文的像素扩散,获取密文。Chai等[6]对图像进行离散小波变换,得到稀疏系数矩阵,并联合Zigzag方法与初等元胞自动机来置乱该矩阵,通过混沌系统产生的测量矩阵对置乱矩阵进行压缩感知,从而获取密文。但是上述技术在反复迭代过程中存在明显的周期性,削弱了加密系统的抗非法攻击能力[7]。
为了解决这个不足,国内外人员提出了光学加密技术,如肖宁等[8]基于离轴圆谐分量展开方法,将明文对应的Gyrator频谱分解成零阶与非零阶圆谐分量,通过球面相位因子,对零阶圆谐分量进行调制,借助迭代相位检索来编码调制结果,获取密文。但是,在其光电结构中,只采用了混沌掩码,存在严重的光轴校准问题,限制了其安全性。Zhu等[9]利用Logistic映射,通过生成多个随机相位掩码,并将其加载到空间光调制器中,准直激光束通过分束器后,得到多个光束,对明文实现干涉加密,并利用离散小波变换将干涉结果变换为稀疏图像,基于鬼成像原理,对稀疏图像完成加密。此技术忽略了明文内容,降低了对明文的敏感性,且无法解决光轴校准问题,使其对外来攻击的鲁棒性不理想。李建军等[10]通过设计复合掩码,并利用Gyrator变换与小波变换所构建的混合小波变换,对明文实施调制,并引入幅度-相位阶段机制,对调制结果实施处理,获取密文,但其鲁棒性不佳,在遇到裁剪攻击时,其复原质量较低。
为了解决光学加密过程中存在的光轴校准问题,并改善其在外来攻击下的复原质量,本文提出了一种非线性光学加密机制。该技术融入了QR码自身强大的纠错与容错能力,可增强密文对外来攻击的鲁棒性。利用SHA-256哈希方法来建立交叉置乱方法,有效增强密文对明文内容的敏感性,再将置乱结果转换为QR码,借助Shearlet变换与安全图像来形成对应的过渡图像,联合Hilbert变换与波带片相位模型,设计调制掩码,通过Gyrator变换与光电装置,对QR码实施加密,输出Gyrator频谱,有效解决光轴校准问题,再借助幅度-相位截断,将Gyrator频谱实施分割,输出密文。最后,验证了所提光学加密方案的安全性与抗攻击能力。
1 Gyrator变换
Gyrator变换[11]是图像领域中常用的2D信号处理措施。令初始信号为fi(xi,yi),则其Gyrator变换模型为
(1)
其中,α是旋转角度;Gα[] 为Gyrator变换;(xi,yi)、 (x0,y0) 分别为初始和输出坐标;O(x0,y0) 是复杂场函数。
为了重构信号,需要对其实施逆处理,因此,式(1)对应的Gyrator逆变换为
G-α(O(xi,yi))=G2π-α(O(xi,yi))
(2)
在Gyrator变换中,当参数α=0时,那么Gα[] 为一种恒等变换;当参数α=π时,Gα[] 等价于式(2)。当α=π/2、α=3π/2时,Gα[] 演变为Fourier变换及其对应的可逆变换。在图像的光学加密过程中,Gyrator变换是依赖一种级联结构来实现的,相应的光学结构如图1所示。其中,图1(a)是式(1)的光学结构,由透镜L1、L2、L3组成,而且相邻二者间的距离都是Z;但是,而透镜L2的焦距是Z/2。P1、P2分别为初始与输出平面。图1(b)代表式(1)的透镜内部结构。α1,α2均为旋转角度,满足如下关系
α1=-α;α2=α-π/2
(3)
当fi(xi,yi) 从P1端进入时,通过Gyrator变换调制后,在P2端可得到相应的Gyrator频谱
(4)
其中,λ是光波波长。
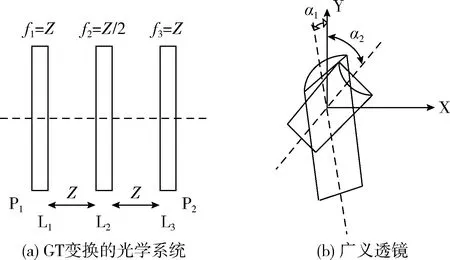
图1 Gyrator变换的光学系统
2 所提光学图像加密算法
所提的基于快速响应码与Shearlet变换的非线性光学图像加密算法过程如图2所示。根据其过程发现,该方案主要分为3个阶段:①基于非线性复合混沌系统的明文置乱与QR码生成;②基于Shearlet变换的QR码分解;③基于Gyrator变换与幅度-相位截断的密文生成。
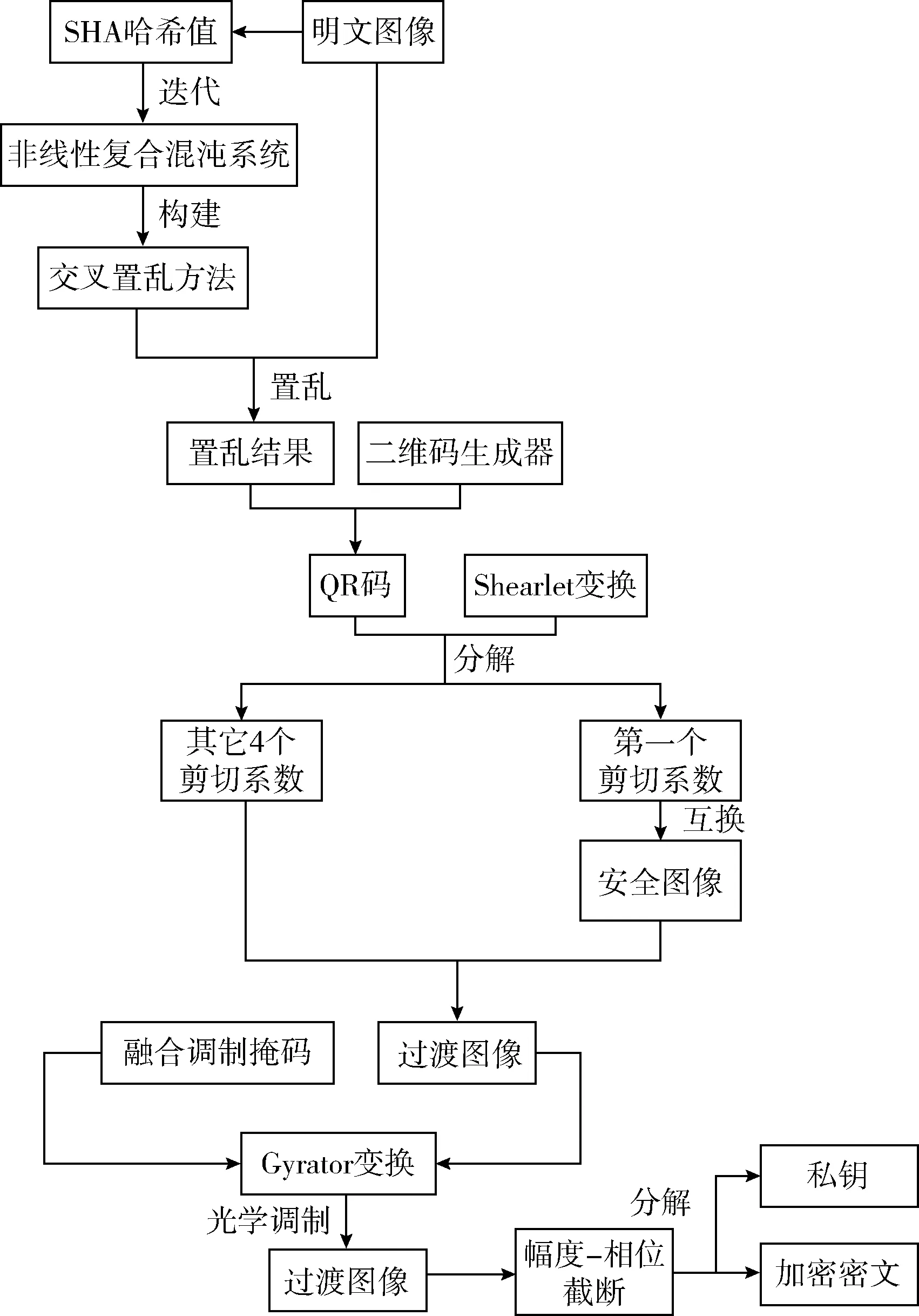
图2 所提光学加密算法的过程
2.1 基于复合混沌系统的明文置乱与QR码生成
本文通过二维码生成器[12]来获取明文f(x,y) 对应的QR码。令明文f(x,y) 的大小为M×N,为了改善加密系统对明文内容的敏感性,借助SHA-256函数[13]来生成明文的哈希值K,再把K分割为子密钥ki
K=k1,k2,k3,…,k32
(5)
为了平衡密文的生成效率及其鲁棒性,引入非线性复合混沌系统来设计交叉置乱方法,其主要由Logistic和Sine两个映射构成[14]
(6)
再根据式(5)中的32个ki来计算3个偏差因子l1、l2与l3

(7)
根据式(7)的l1、l2和l3,生成式(6)的初始条件u0、x0和y0

(8)
其中,u′0、x′0与y′0均为用户预设初值;mod是求余运算符号;⊕代表异或运算。
通过对式(6)迭代M×N次,可形成两个序列X={x1,x2…xM×N}、Y={y1,y2…yM×N}。 随后,分别在X={x1,x2…xM×N}、Y={y1,y2…yM×N} 中选择前M×N/2、 后M×N/2个元素,并将其依据升序方法组合成新的数组Z={z1,z2…zM×N}。 引入交叉运算[15],构建像素交叉置乱方法
ai=i+mod(floor(z(i+1000)×1010),M×N-1),i∈[1,M×N]
(9)
[P(i),P(ai)]=swap{P(i),P(ai)}
(10)
其中,ai为待交叉的位置;P(i) 为第i个像素的灰度值;floor() 是向下取整操作;swap为交叉运算符号。
在所提的加密方案过程中,主要依据式(9)和式(10)来改变QR码的像素位置。以图3(a)为样本,其经过交叉置乱后,形成的结果如图3(b)所示;随后,根据二维码生成器,形成对应的QR码,如图3(c)所示。

图3 置乱结果及其对应的QR码
2.2 基于Shearlet变换的QR码分解[16]
为了提供图像的多分辨率分析,本文引入离散Shearlet变换(discrete Shearlet transform,DST)来处理QR码。DST是一种新的多尺度方向离散表示方法,主要有多尺度表示和捕获多维数据的两种能力,其过程如图4所示。它是一个包含单母剪切函数的仿射系统,通过缩放、剪切和平移等参数化来捕获奇点的方向。在图像处理中,DST主要是依赖拉普拉斯金字塔和方向变换来实现的,令图像为I,其对应的DST映射为
I→SHφI(a,s,x)
(11)
其中,a>0为尺度参数;s为方向参数;x为位置参数;φ为母剪切函数;SHφ为剪切变换,其函数如下
(12)
根据文献[16]可知,剪切主要是通过膨胀、剪切和平移来产生的。对于每个母函数φ,其剪切函数为
φj,k,m(x)=|detA|j/2φ(BkAjx-m)∶j,k∈Z,m∈Z2
(13)
其中,j为尺度因子;k为剪切方向数量;m是平移量;φ为母剪切函数;SHφ为剪切变换,A,B是2×2的可逆矩阵,分别表示膨胀与几何变换
(14)
其中,b的经典取值为4;s的经典取值为1。
因此,对于每个母函数φ,其DST变换为
SH{φj,k,m=2(3/4)jφ(SkAj-m)∶j,k∈Z,m∈Z2}
(15)
对于母函数在特定水平下的DST,若其分解系数的总量为n,则其方向剪切矢量d(i) 的长度为
d(i)=[x1,x2,x3…xl]
(16)
根据式(16)可知,对于第i级DST分解,则其生产的剪切系数总量为
n=2x1+2x2+…2xl+1
(17)
例如,当d(i)=[1 1] 时,则n=21+21+1=5。 在本文加密方案中,选择5级DST分解,从而可获取5个剪切系数C1,C2,C3,C4,C5。
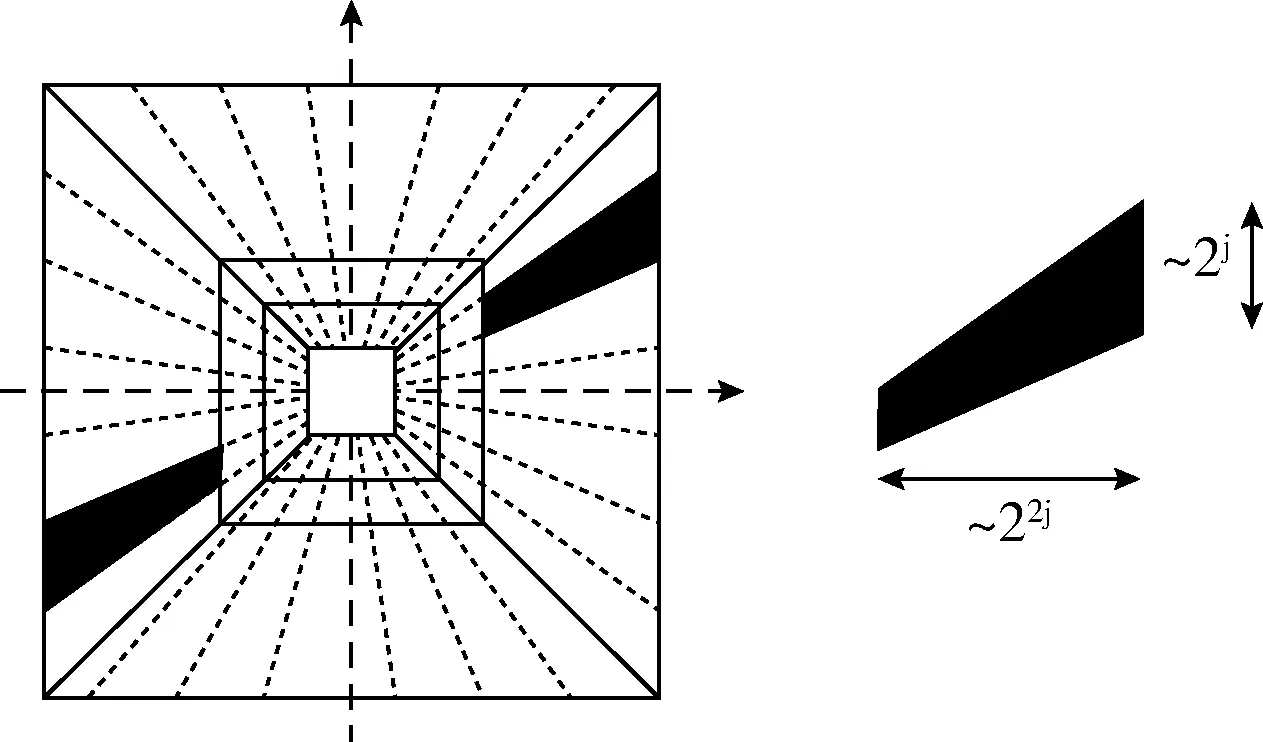
图4 Shearlet变换的分解
为了改善加密系统的安全性,本文设置一个安全密钥图像,将其与剪切系数C1实施交换,再根据可逆Shearlet变换,联合剩余的4个系数C2,C3,C4,C5,可输出一个过渡图像。以图5(a)为密钥图像,根据上述过程,形成的结果如图5(b)所示。

图5 过渡图像的生成
2.3 基于Gyrator变换与幅度-相位截断的密文生成
在光学加密装置中,普通的混沌相位掩码会引起光轴对准问题[10],限制了密文的安全性。故在所提方案中,引入Hilbert变换[10]与波带片相位模型来设计调制融合掩码,通过二者的自身特性来实现光轴校准。Hilbert变换的任意径向线存在一个Pπ弧度的相对位误差[10],有助于对准光学装置的轴线,其模型为[10]
H(r,φ)=exp[ipφ]
(18)
其中,p是阶数;(r,φ) 代表Cartesian坐标,计算函数为

(19)
而波带片相位模型中含有一个聚焦环,可作为光电装置中的衍射光学元件,能够与光轴对齐[17]
(20)
其中,λ代表光波波长;g是透镜焦距。
随后,联合H(r,φ)、R(r,φ),设计一个融合调制掩码
(21)
根据式(21)输出的R(r,φ),基于Gyrator变换,以及图6所示的光电混合装置,对过渡图像I′(x,y) 实施调制
IC(u,v)=Gα(I′(x,y)×S(r,φ))
(22)
其中,IC为加密结果。
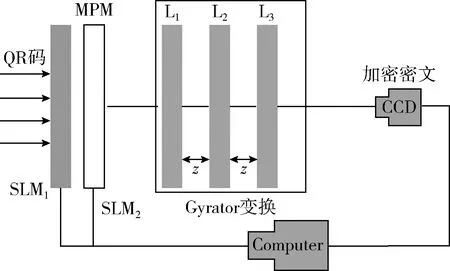
图6 所提的光电混合装置
最后,为了破坏加密系统的线性关系,本文引入幅度-相位截断[18]方法,对IC实施处理,从而得到最终密文
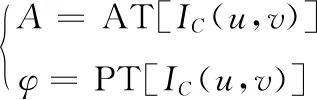
(23)
其中,PT代表相位截断;AT代表幅度截断;A是幅度信息;φ是相位信息,作为私钥。
根据文献[10]和文献[17]中的经典参数,设置p=1,r=3,g=40mm,λ=632.8mm,通过式(18)~式(21),构成的H(r,φ)、R(r,φ) 与S(r,φ) 分别如图7(a)~图7(c)所示。通过式(18)的加密,输出结果如图7(d)所示。利用式(23)来处理图7(d),得到的幅度与相位信息分别如图7(e)~图7(f)所示。

图7 加密效果测试
3 实验结果与分析
为了验证本文光学加密方案的优势,通过Matlab 7.0平台来实施测试,并将新颖的光学加密机制当作本次测试的对照组,分别是文献[9]和文献[10],此二者都是非线性光学加密方案,能够较好地用于灰度与彩色明文的加密,具备较好的安全性,且实验平台也为Matlab。因此,文献[9]和文献[10],与所提算法具备较好的可比性。实施测试的参数为:μ′0=3.92,x′0=0.35,y′0=0.52,n=5,p=2,r=3,g=50mm,λ=632.8mm。
3.1 光学加密效果测试
将图8(a)作为此次实验的样本,借助所提方案、文献[9]与文献[10]技术对其实施光学调制,获取的密文如图8(b)~图8(d)所示。由测试效果发现,3种方案都能够较好地隐藏明文信息,人眼无法清晰看到明文的相关内容,具备较好的安全保密性。为了客观评估三者的安全性差异,引入密文熵值[2]来衡量,计算数据见表1。由输出数据发现,所提方案的加密结果具有更大的熵值,达到了7.997,与理论值“8”非常接近,而文献[9]、文献[10]方案的密文熵值分别为7.984、7.992,都要小于本文方案。因此,相对于文献[9]和文献[10]而言,所提光学加密方案具有更高的保密安全性。这主要是因为所提方案采用了Shearlet变换来分解明文对应的QR码,并利用与明文不同的安全图像来替换剪切系数,利用Hilbert变换与波带片相位模型构建的融合掩码,借助Gyrator变换来实施光学调制,而且引入了幅度-相位截断方法来破坏密文的线性关系,使其具备理想的安全性。文献[9]虽然是采用压缩鬼影与多路光束干涉来实施明文的加密,但是在光电混合装置中,只利用混沌相位掩码,易引起严重的光轴校准问题,使其安全性不佳。而文献[10]则是利用混沌相位掩码与螺旋掩码来构建调制掩码,通过Gyrator小波变换来获取密文,其考虑了掩码的随机性,并能解决光轴校准问题,但该技术是直接将光束作用于明文,限制了其安全性。

图8 3种方案的加密结果

表1 密文熵值测试
3.2 抗选择明文攻击能力测试
选择明文攻击是当前加密算法常遇到的攻击手段,攻击者可利用明文攻击方法和大量的测试实验来解密密文,给加密系统带来了风险[2]。由国内外相关研究结果发现,NPCR、UACI曲线是衡量密文对选择明文攻击的鲁棒性的经典指标,二者的计算模型为[10]
(24)
(25)

(26)
其中,W×H是密文尺寸;I是初始明文对应的密文;I′是修改明文对应的密文,且其与I之间只有1个像素不同。
将图8(a)当作此次实验的样本,记为I,把位于(98,84)处的像素值59改为95,从而得到一个新的图像,标记为I′;再借助所提方案、文献[10]和文献[9]对I与I′实施光学调制,形成相应的加密结果;随后,通过式(24)~式(26),得到3种技术的NPCR、UACI曲线,相关数据如图9所示。根据统计数据发现,文献[10]加密方案具有更高的抵御明文攻击能力,另外,本文方案对明文攻击也具有相近水平的鲁棒性,但是,文献[9]对选择明文攻击的鲁棒性最低。在图9中,文献[10]的稳定NPCR=99.27%、UACI=35.73%,所提方案的稳定NPCR=98.94%、UACI=35.54%,而文献[9]的稳定NPCR=96.75%、UACI=35.16%。 这主要是因为文献[10]算法与所提方案的调制掩码都与明文内容相关,增强了系统对明文内容的敏感性,但是由于文献[10]的Gyrator变换的旋转角度也是依赖明文信息来计算的,从而使其对选择明文攻击的鲁棒性更高。而文献[9]方案的整个光学加密过程都忽略了明文内容,使其对明文修改缺乏敏感性。
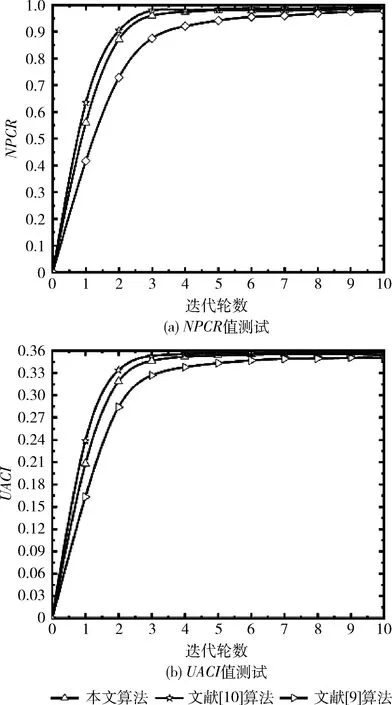
图9 抵御选择明文攻击能力测试
3.3 密钥敏感性测试分析
密钥敏感性是客观衡量加密系统安全性的重要指标,需要满足严格的“雪崩效应”[7]。故在此次实验中,本文验证了μ′0=3.92的敏感性。借助修改因子Δ=10-16来调整μ′0,形成 (μ′0-Δ) 与 (μ′0+Δ)。 再联合其它密钥,得到3组测试数据。最后,利用这3组密钥,对图8(b)实施复原,并统计了不同μ′0的对应的MSE(mean square error)值,结果如图10所示。观察图10(a)和图10(b)发现,即使对μ′0实施10-16的调整,这种错误密钥也是不能复原图像,所得的结果均不能清晰地看到明文内容,对应的MSE值均大于3500;观察图10(c)发现,只有完全无误的密钥才能对图9(b)实施复原,获取相应的QR码与清晰的明文内容;这种情况下的MSE值趋于0,如图10(e)所示。这组实验数据显示了本文方案具有较好的敏感性,符合 “雪崩效应”。

图10 密钥敏感性测试
3.4 噪声与裁剪攻击的鲁棒性测试
为了测试加密系统对噪声攻击的鲁棒性,将不同程度的高斯噪声作用于图8(b)~图8(d),得到的攻击结果为
E′=E(1+KN)
(27)
其中,E′为攻击后的密文;K代表噪声强度系数;N为高斯噪声。
不同强度噪声干扰下的密文复原效果如图11所示。根据测试数据发现,当噪声干扰程度越大时,3种方案的复原图像的MSE值越大。但是,所提方案对噪声具备更强的鲁棒性,在噪声干扰强度增大时,其复原图像的MSE值较为平稳,而文献[9]和文献[10]在轻度噪声攻击时可获取较为满意的复原质量,但是,当噪声强度超过0.6时,其复原图像质量较差,对应的MSE值迅速增大。例如,当噪声强度为0.7时,所提方案的复原图像对应的MSE值仅为155.60,而文献[9]和文献[10]的MSE值分别为493.33、358.53。此次实验数据充分显示了所提方案对噪声具有更好的鲁棒性。
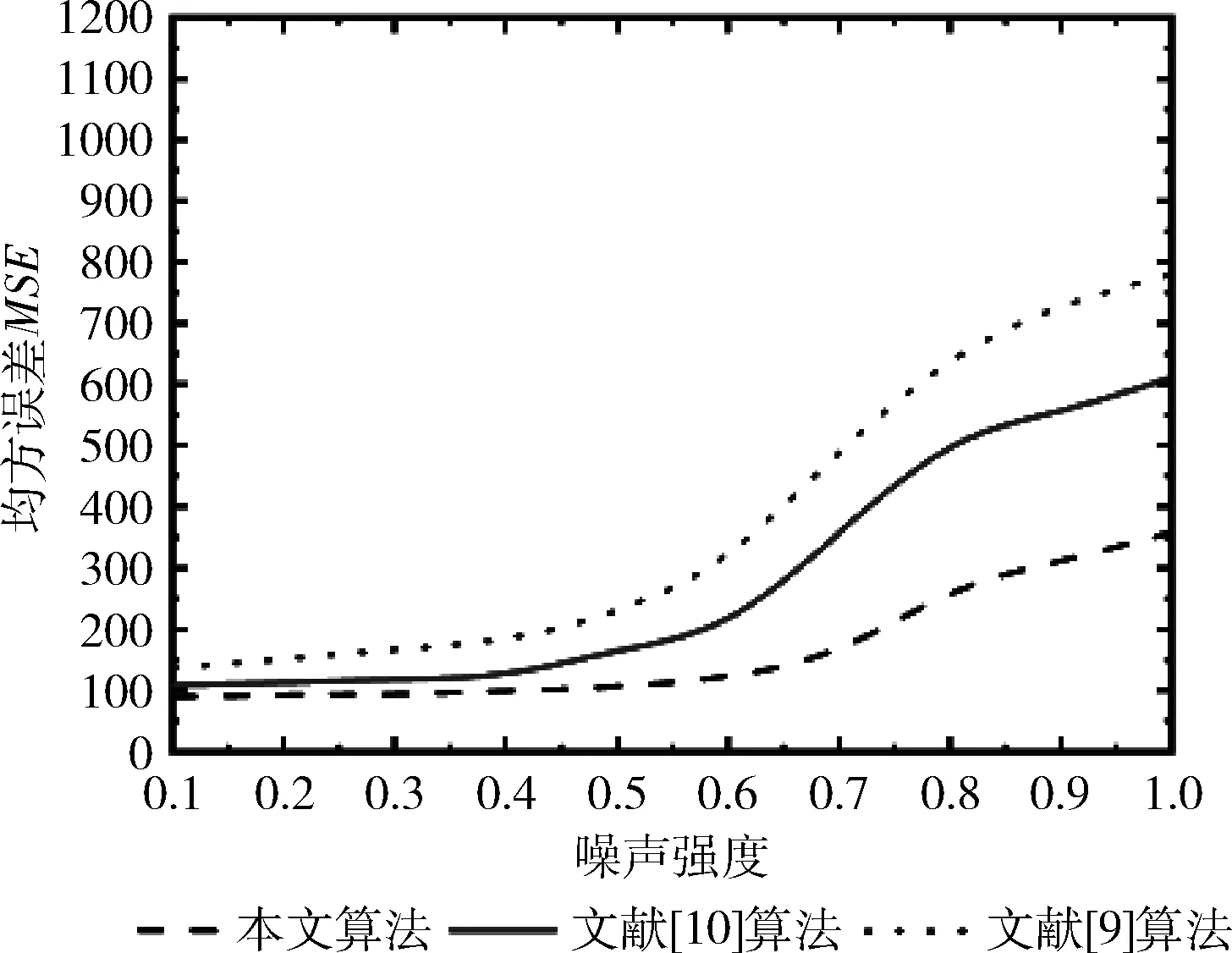
图11 不同光学加密方案的抗噪攻击能力测试
剪切攻击也是衡量加密技术鲁棒性的重要指标[8]。所以,以图8(b)~图8(d)为对象,对其作用于相同程度的剪切攻击,形成的干扰密文,如图12(a)、图12(c)、图12(e)所示,随后,借助所提方案与文献[9]、文献[10]方法,对三者实施复原,得到的结果如图12(b)、图12(d)、图12(f)所示。根据输出结果发现,所提算法对剪切攻击具备更强的鲁棒性,其复原质量最佳,细节清晰可见,只有轻微模糊现象,如图12(b)所示。而文献[9]的复原质量较低,丢失了大量的细节信息,如地面上的文案,如图12(e)所示。文献[10]的抗裁剪攻击能力也不理想,其复原质量要低于所提方案,存在模糊现象,如图12(d)所示。

图12 不同方案对裁剪攻击的鲁棒性测试
4 结束语
为了解决光学加密方案的光轴校准问题,并提高加密系统对裁剪等攻击的鲁棒性,本文提出了基于快速响应码与Shearlet变换的非线性光学图像加密算法。所提方案是将激光器的光束作用在QR码上,充分利用QR码的纠错与容错特性来增强密文对噪声与裁剪的鲁棒性。通过利用一个与明文不同的安全图像来替换Shearlet剪切系数,以及借助幅度-相位截断机制来增强所提方案的非线性特征。另外,为了提高密文对明文的攻击鲁棒性,利用SHA-256哈希方法与非线性复合混沌系统来置乱QR码,使其对明文内容具备较高的敏感性。同时,通过构建融合掩码,借助Gyrator变换对置乱QR码实施调制,有效解决光电加密装置的校准问题。通过多组实验测试数据显示:所提加密方案具备较高的保密安全性与敏感性,对噪声、裁剪与明文攻击具备较好的鲁棒性。
