MIMO-OFDM信号参数盲估计方法
2020-05-22范聪聪张天骐梁先明
范聪聪,张天骐,梁先明
(1.重庆邮电大学 通信与信息工程学院,重庆 400065;2.中国西南电子技术研究所,四川 成都 610036)
0 引 言
正交频分复用(orthogonal frequency division multiplexing,OFDM)是一种多载波调制技术,其子载波之间相互正交且部分重叠,因此在频谱的利用率方面有很大的提升;MIMO技术可以改善数据的传输速率;将两者结合的MIMO-OFDM技术继承了它们的优势[1]。在非协作通信中,必须知道信号的参数以分析截获的信号,因此对MIMO-OFDM信号参数的盲估计具有重要意义。
目前文献对MIMO-OFDM信号的同步、峰均比抑制以及信道估计[2-5]研究较多,而对参数估计鲜有涉及。文献[6]利用最大似然函数结合动态粒子群优化的方法估计OFDM信号的符号周期,但未对信号的子载波参数进行估计;文献[7]首先利用盲源分离的思想去除分布式MIMO-OFDM系统中信道的干扰,进而对载波的频偏进行估计;文献[8]推导了不同调制模式下OFDM的四阶循环累积量的理论值,通过设置相应的阈值完成对子载波调制方式的识别,该方法可有效抑制噪声对计算结果的影响;文献[9,10]验证了OFDM的周期平稳性,并对其进行了参数的估计以及子载波调制方式的识别;文献[11,12]在单接收天线下利用高阶统计量的方法识别MIMO系统中的空时编码方式。
本文首先建立MIMO-OFDM信号的模型,然后对它的循环自相关函数进行推导,通过对3维图切面的分析,可得到符号周期等相关参数。接着又对它的四阶循环累积量进行推导,通过分析可得到子载波相关的参数。最后分别对两个算法进行仿真验证及性能分析。
1 信号模型
根据发送和接收天线之间位置的不同,可将MIMO-OFDM系统分为两种:分布式和集中式,本文研究集中式MIMO-OFDM系统,该系统中收发两端放置的天线相对集中。图1为MIMO-OFDM信号的生成框架,发送数据经处理后得到多路并行的OFDM信号,再由多根天线发送出去。
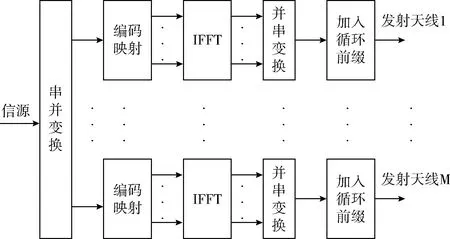
图1 MIMO-OFDM信号流程
发送端第i根天线上产生的OFDM信号xi(t) 为
(1)
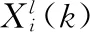
(2)
在集中式 MIMO-OFDM 系统中,接收天线以集中方式放置,因此可以忽略它们之间的距离,各路信号以叠加方式同时到达接收端。在不考虑频偏和初始延时的情况下,第m个天线接收到的信号为

(3)
式中:n(t) 为平稳高斯白噪声,且与信号独立。nT为发射天线数量。本文以r(t)为例进行分析。
2 算法原理
2.1 循环自相关算法
复信号x(t) 的自相关函数可表示为
(4)
式中:τ表示时延,E[·] 表示求期望,*表示取共轭。若Rx(t,τ) 是t的周期函数,则Rx(t,τ) 可展开成Fourier级数形式
(5)
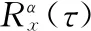
(6)
2.2 四阶循环累积量算法
信号x(t) 的k阶矩表示为
Mkx(τ1,τ2,…,τk-1) = E[x(n)x(n+τ1)…x(n+τk-1)]
(7)
式中:τ1,τ2,…,τk-1表示时延,x(t) 的k阶样本循环矩可表示为
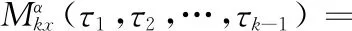
(8)
式中:T表示观测时间,〈·〉t表示关于时间求均值,N表示采样点数。x(t) 的四阶循环累积量为
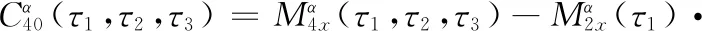
(9)
当τ1=τ2=τ3=0时,可得

(10)
3 MIMO-OFDM的循环自相关函数分析
为便于计算,定义非对称自相关函数为
Rx(t,τ)=E[x(t)x*(t+τ)]
(11)
第m个接收天线上的MIMO-OFDM信号r(t) 的自相关函数为
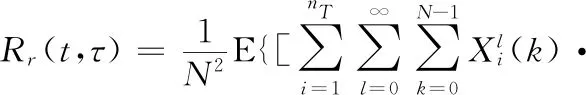
(12)
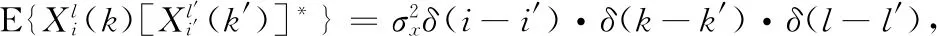

(13)
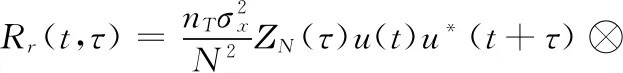
(14)
分析ΖN(τ) 可得,当τ为Tu的整数倍时,ΖN(τ)≠0,又根据u(t) 的特点,当0≤|τ|≤Ts时,使Rr(t,τ) 不等于零的τ值只有0,±Tu,即Rr(t,τ) 仅在τ=0,±Tu时存在非零值。
根据文献[10]可得Rr(t,τ) 是周期函数,周期为Ts,所以MIMO-OFDM信号存在循环自相关函数。根据
(15)
式中:FT[·]表示Fourier变换,对Rr(t,τ) 进行Fourier变换,可得循环自相关函数为
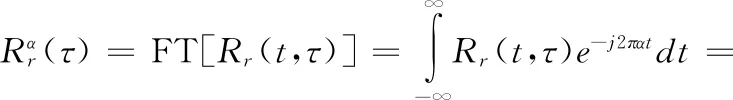
(16)
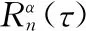
4 MIMO-OFDM的四阶循环累积量分析
由于所有发射天线上的OFDM信号采用相同的调制方式,所以各天线上的子载波只有幅度不同,而频率和相位均相同,因此第i个发送天线上的OFDM信号xi(t) 也可表示为如下形式
(17)
式中:fn为第n路子载波的频率,基带相位为θn,Pi,n(t) 为天线i上第n路子载波的幅度。
第m个接收天线上的信号可表示为
(18)
式中:φn为初始相位偏差。
当阶数大于2时,噪声n(t) 的高阶循环累积量等于0,在计算中可以忽略。由于天线间彼此独立,子载波间也彼此独立,因此接收信号的四阶循环累积量可以表示为多个发射天线上多路子载波信号的叠加。根据等式(10)和式(18)可求得MIMO-OFDM的四阶循环累积量为
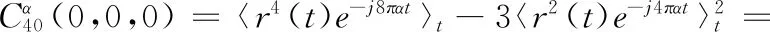
(19)
式中:Qn(t)=P1,n(t)+P2,n(t)+…+PnT,n(t) 是各发射天线上第n路子载波幅度之和。
当α取值为子载波频率 (α=fk) 时
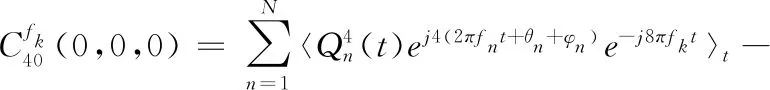
(20)
当α≠fk时
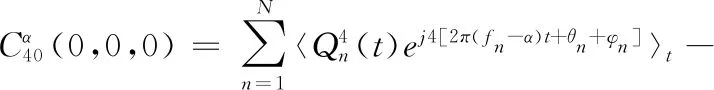
(21)
因此,MIMO-OFDM的四阶循环累积量为
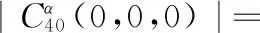
(22)
式中:|·| 表示取模值。
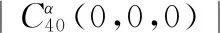
5 计算机仿真
由于对信号进行分析时选取的是任意单个天线接收的数据,所以以下各仿真实验中接收天线数均为1。
实验1:循环自相关算法估计Ts、Tu和Tg。 信息码的数量是3600,发射天线数nT取2和4,子载波数N=12,子载波均为4PSK调制,循环前缀长度为N/4,符号周期Ts=10μs,信号带宽1.5 MHz,4倍过采样,信道为高斯白噪声信道,信噪比SNR=-10dB。
图2为nT=2时MIMO-OFDM的循环自相关三维图。图中对幅值进行了归一化处理,从图中可以看出,α=0,τ=0处的幅值远高于其它位置,这是由于噪声仅在该处对信号有影响,噪声和信号叠加造成的。
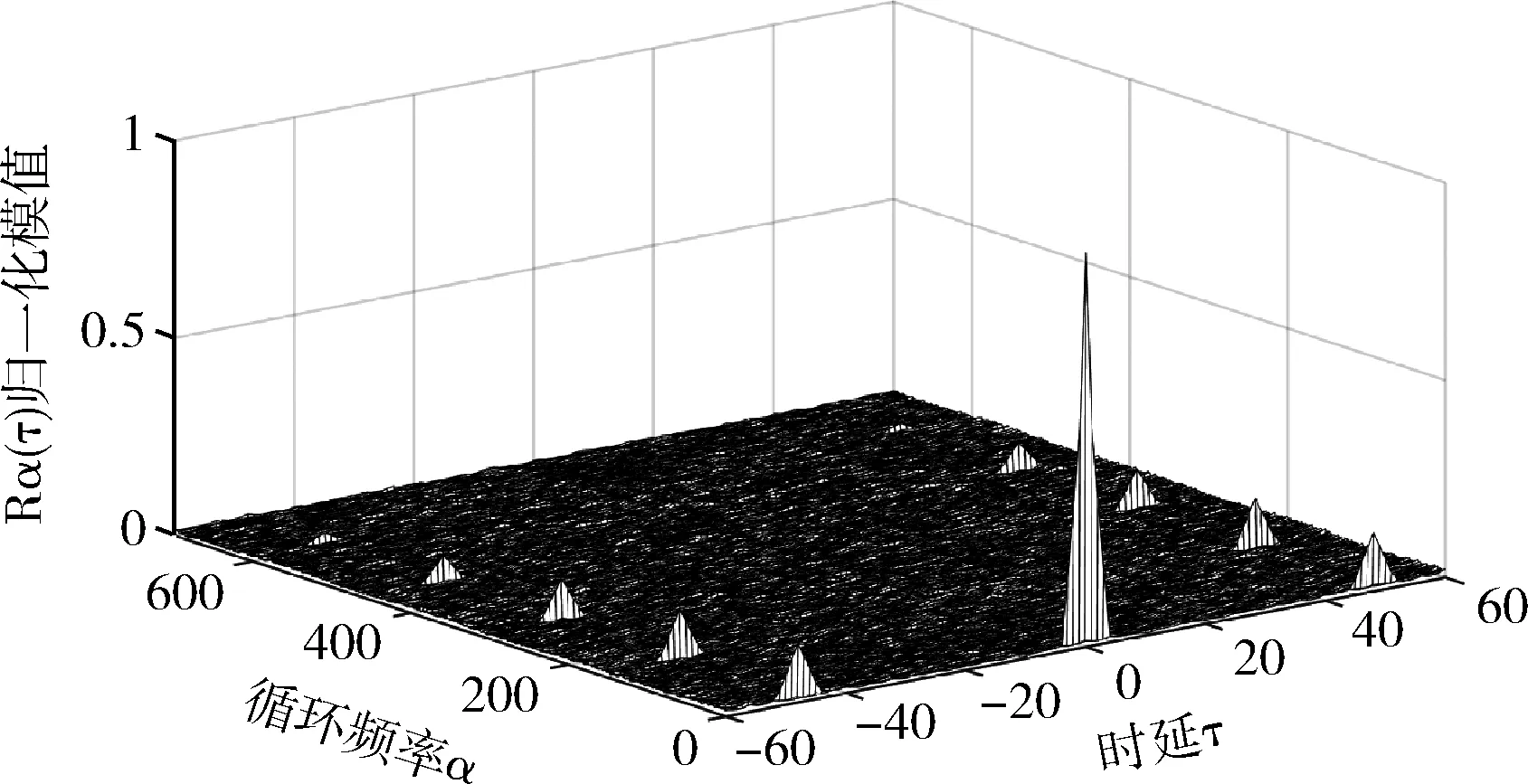
图2 MIMO-OFDM的循环自相关(nT=2)
图3为循环自相关函数在α=0处的切面。由于过采样的影响,主峰处出现了一些小的副峰。从图中可以看出,峰值出现在τ=0,±Tu处,通过检测峰值之间的距离可以得到MIMO-OFDM的有用符号时间Tu=8μs。
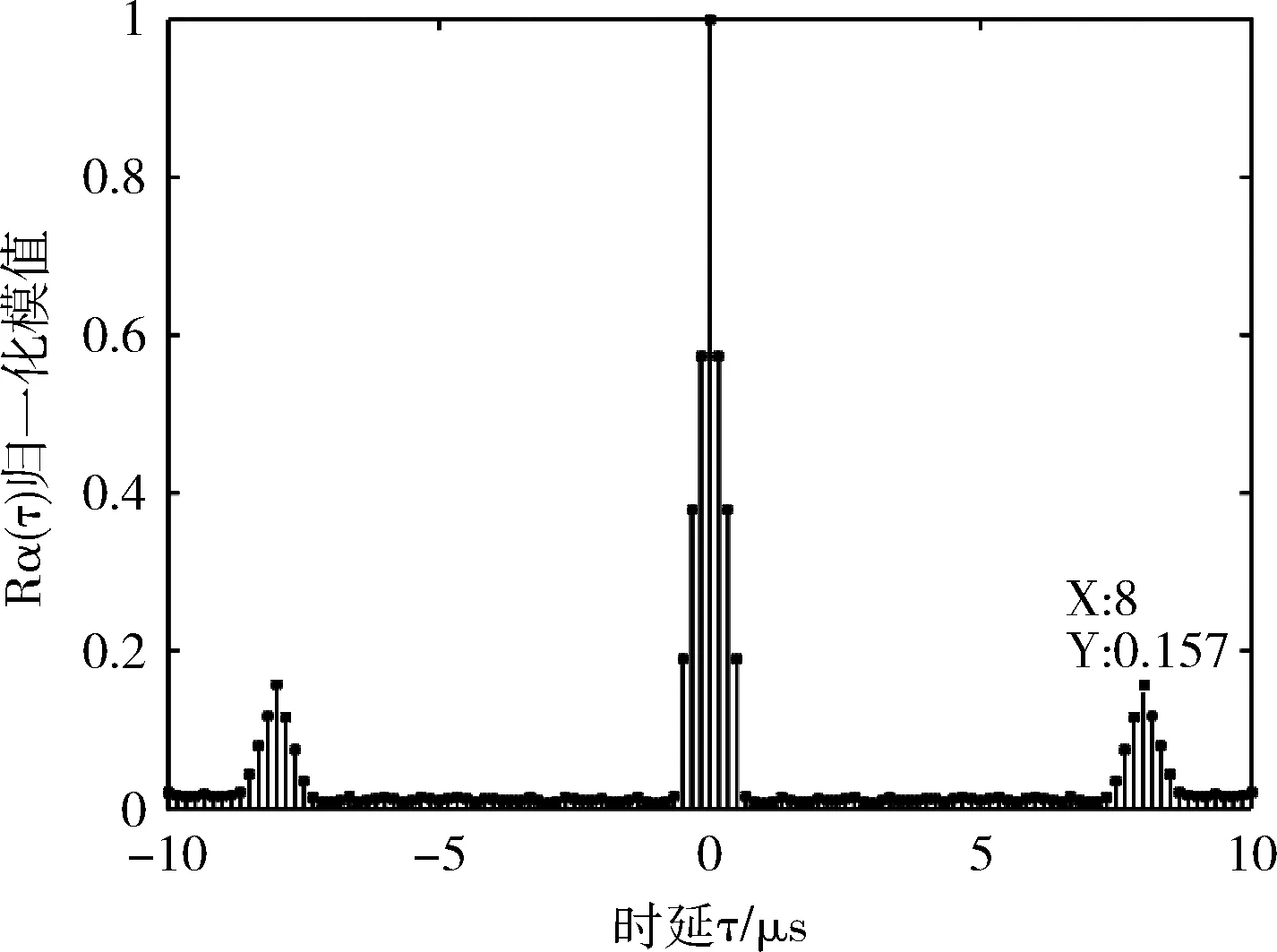
图3 α=0切面(nT=2)
图4为循环自相关函数在时延τ=Tu处的切面。图中峰值间距记为Δα,由Δα=1/Ts可得Ts=10μs。 再利用Tg=Ts-Tu可得循环前缀时间Tg=2μs,所得结果与仿真设置的参数一致,验证了理论分析的正确性。
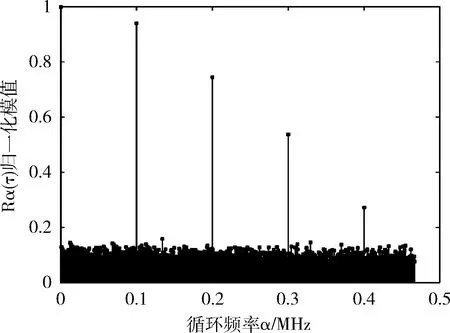
图4 τ=Tu切面(nT=2)
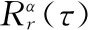
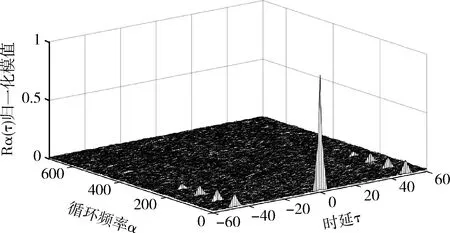
图5 MIMO-OFDM的循环自相关(nT=4)
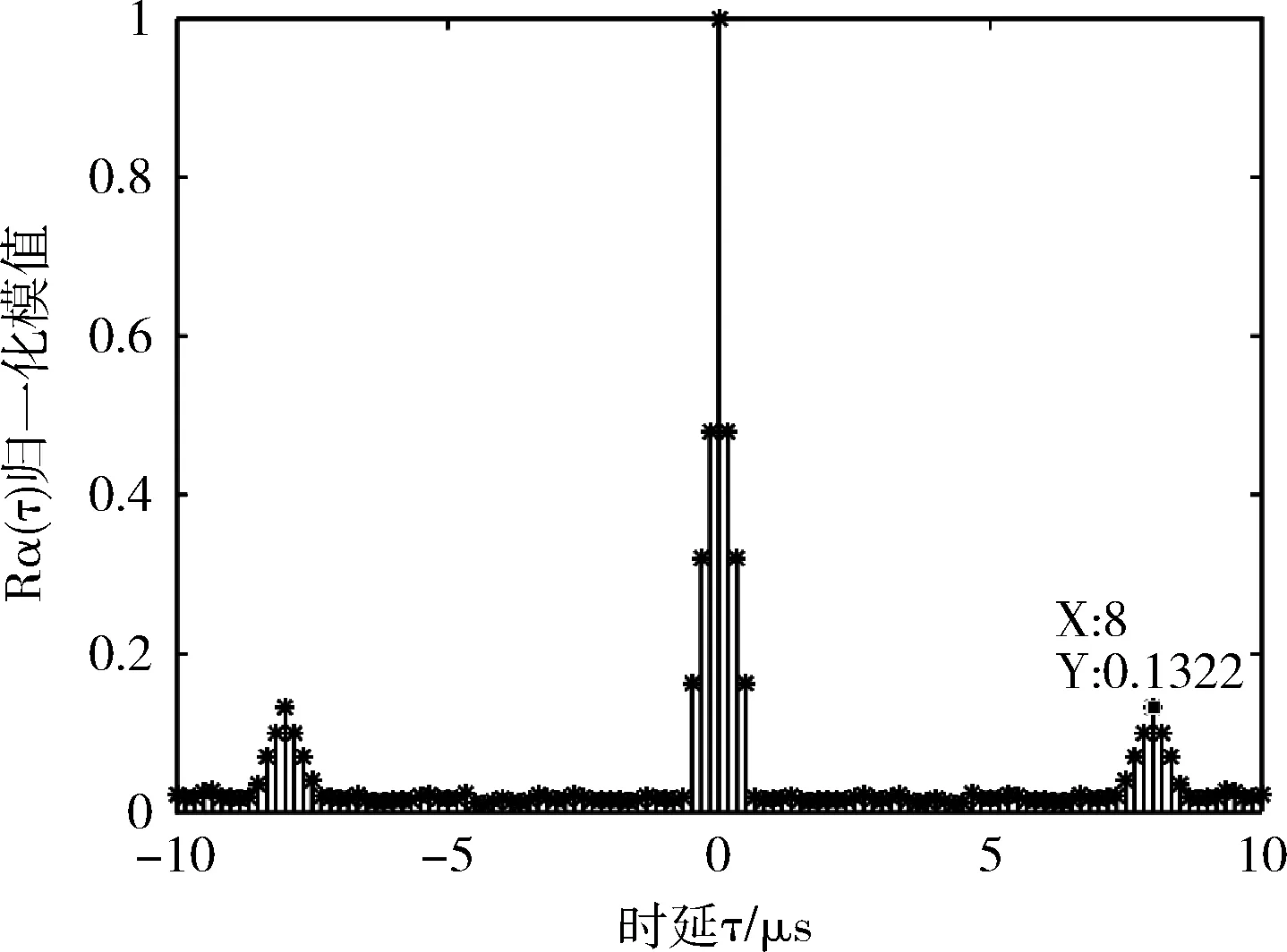
图6 α=0切面(nT=4)
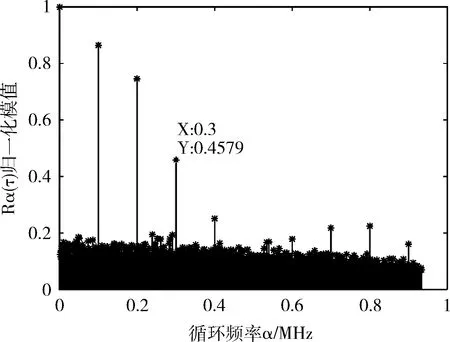
图7 τ=Tu切面(nT=4)
实验2:算法性能分析。在不同SNR以及不同nT下检测Tu和Ts的正确估计概率,nT分别取2,3,4,SNR的范围为-25 dB~-5 dB,其余参数设置与实验1相同,400次Monte Carlo仿真。
图8为不同SNR及不同nT下Tu的正确估计概率曲线。从图中可以看出,当nT增加时,算法对Tu的估计性能虽然有些下降,但在SNR>-11dB时,不同nT下Tu的正确估计概率均达到100%。

图8 Tu的正确估计概率曲线
图9为Ts的正确估计概率曲线,其性能与图8类似。在SNR>-9dB时,不同nT下Ts的正确估计概率均达到100%。从性能曲线可以得出,循环自相关算法可在低SNR下对Tu和Ts进行有效估计。
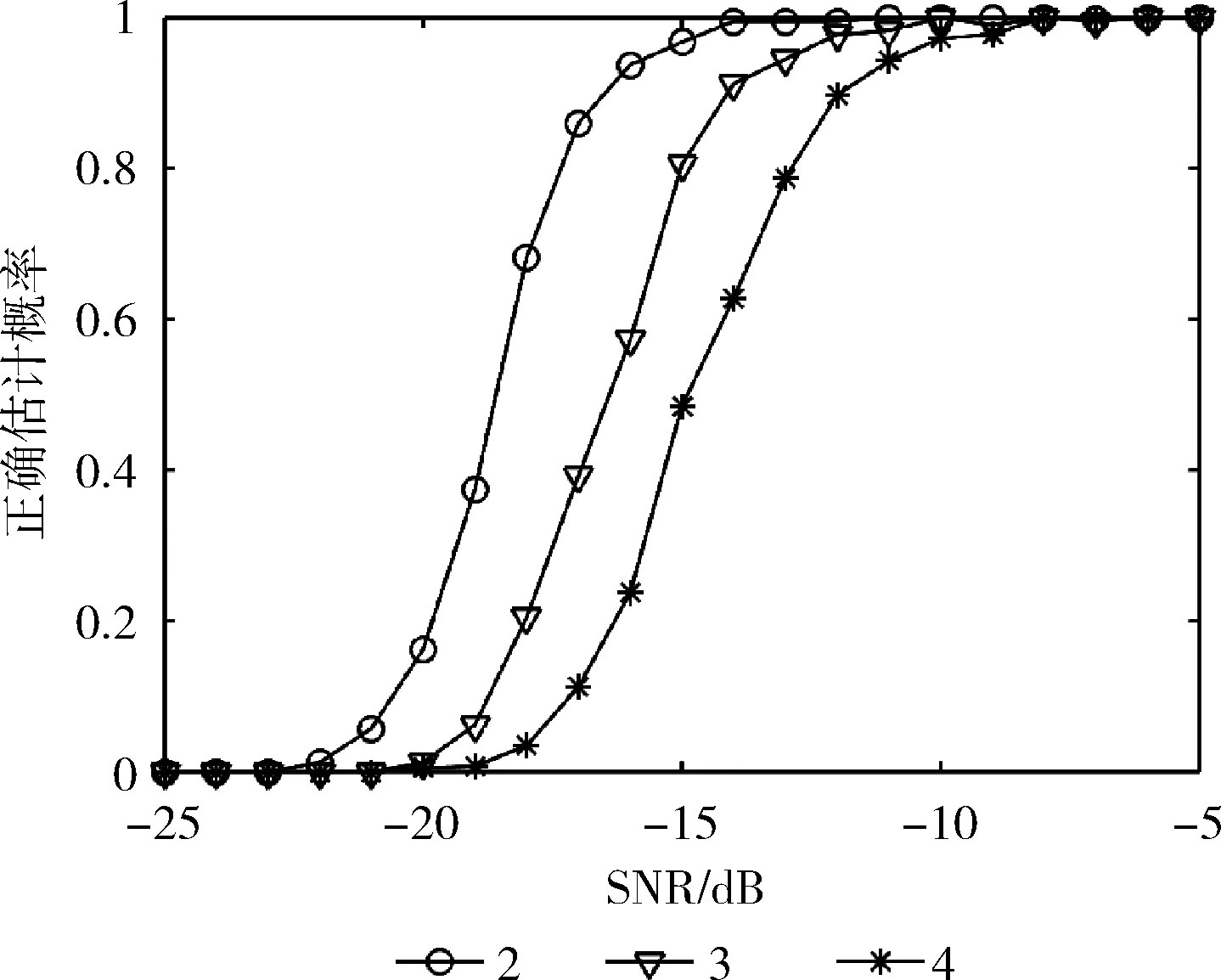
图9 Ts的正确估计概率曲线
比较图8和图9可以发现,在相同发射天线数下,Tu的估计性能要好于Ts,这是因为在估计Ts时,对自相关函数进行了一次Fourier变换,其性能与Fourier变换的点数有关,点数越多,估计性能越好。
实验3:验证四阶循环累积量算法。子载波数N=12,子载波初始频率为6 kHz,频率间隔为0.2 kHZ,SNR=-5dB,其余参数与实验1相同。
图10为nT=2时MIMO-OFDM的四阶循环累积量,从图中可以看出,当α=fk时会出现峰值,峰值间隔为0.2 kHz。由峰值的数目可得N=12,由峰值对应的α值可得各子载波的频率,其中第1个子载波的频率为6 kHz,第12个为8.2 kHz,仿真结果与设置的参数一致。

图10 MIMO-OFDM的四阶循环累积量(nT=2)
图11为nT=4时的仿真图,由图也可得出子载波的参数,从而说明了算法的正确性。
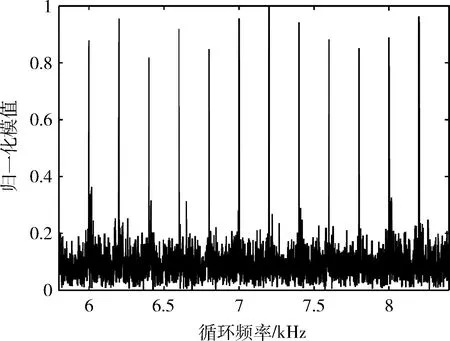
图11 MIMO-OFDM的四阶循环累积量(nT=4)
实验4:算法性能分析。在不同SNR以及不同nT下检测子载波参数的正确估计概率。nT分别取2,3,4,SNR的范围为-15 dB~5 dB,其余参数设置与实验1相同,400次Monte Carlo仿真。
图12为不同SNR和不同nT下子载波参数的正确估计概率曲线。从图中可以看出,当nT增加时,其估计性能虽有下降,但在SNR>-3dB时,不同nT下的子载波参数正确估计概率均能达到100%。

图12 子载波参数的正确估计概率曲线
6 结束语
本文研究了非协作通信中MIMO-OFDM信号参数的盲估计方法。利用循环自相关算法,可估计出符号周期、有用符号时间以及循环前缀时间;利用四阶循环累积量算法,可估计出子载波的数量以及频率。从仿真结果可以得出,在不同发射天线数下,所提算法均可在较低信噪比下准确估计出信号的各项参数。本文仅分析了集中式MIMO-OFDM系统,而关于分布式MIMO-OFDM系统,由于其天线位置较分散,会引入更多的干扰,对其参数的盲估计将更加复杂,是下一步研究的重点。
