液压振动挖掘试验与分析

(福建农林大学 机电工程学院， 福建 福州 350002)

引言

目前世界上各类施工工程中，利用液压挖掘机完成的土方挖掘作业量大约占总挖掘量的65%～70%[1-2]。据统计，到2017年底,我国工程机械主要产品保有量约为690～7747万台[3]。因此，液压挖掘机的发展对推动社会建设、经济发展具有着重要意义。振动掘削在农业机械得到广泛运用，如马铃薯振动挖掘机[4-5]、根茎类中药材振动挖掘机[6-7]、振动式花生收获机[8-9]等。并且国外关于振动挖掘减阻很早就进行了研究，其中YOW等[10]对一维正弦振动耕作进行了实验和理论分析得到同一运动速度下，振动可以使最大切削阻力减低40%。GUPTAR等[11]利用振荡耕作工具产生不同的振幅和频率对土壤进行破碎效果的试验分析。RADITE等[12]利用振动技术降低潜耕机牵伸要求的试验研究。ZENKOW等[13]在零下温度下，建立振动挖掘对地面运动关系的数学模型，分析高频振动对地面滑动阻力的影响。国内对于振动挖掘机的研究仍处于理论研究阶段，振动减阻理论研究还不够完善，振动挖掘技术的运用研究还不够成熟。针对振动挖掘特性，对振动挖掘试验平台进行土壤的试验研究，分析振动参数与挖掘阻力之间的变化关系，并获得土壤的最佳振动挖掘参数。研究结果将有助于推动振动挖掘技术在液压挖掘机上的运用和发展，使得液压挖掘机更加适应社会发展需求。

1 振动挖掘机的结构及原理

1.1 振动减阻机理

液压振动挖掘装置具有双作用切削土壤特点：当土壤被切削时，不仅受到装置前进方向上的切削力，还受到垂直于前进方向上的作用力；切削完的土壤随着装置一起振动，土壤振动时会吸收部分振动能量使自身内应力变大，内应力越大，土壤越容易破碎[14]。振动式挖掘作业过程相对于振动式挖掘是对土壤快速剪切的挖掘，在对土壤进行有无振动剪切试验中，大量的试验数据表明[15]：在保持土壤的竖向应力不变且都有一定压缩的条件下，快速剪切所得到的土壤内摩擦角φ的值较小，抗剪强度较小。并且慢速剪切所测得的土壤内摩擦角和抗剪强度都相对较大，从而振动能够使得土壤的抗剪切强度、土壤间摩擦力、粘附力下降，从而使得挖掘阻力下降。

1.2 振动挖掘机的结构

液压振动挖掘装置的结构图，如图1所示；振动方式原理，如图2所示。装置利用串联振动液压缸的振动方式，可以通过控制振动液压缸的往复收缩，作用与铲斗使得铲斗产生振动，再利用原有的铲斗油缸的伸缩，推动振动油缸整体向前作用在铲斗上，此时铲斗油缸的作用与振动油缸的作用就会进行叠加，从而实现完整振动挖掘作业。如果振动油缸保持不动，可将振动油缸等效为连杆，此时铲斗油缸推动振动油缸对铲斗进行作用，只产生铲斗的静态挖掘动作力，此时即为常规的挖掘作业。

1.斗杆臂 2.铲斗油缸 3.振动油缸 4.铲斗图1 液压振动挖掘装置结构示意图

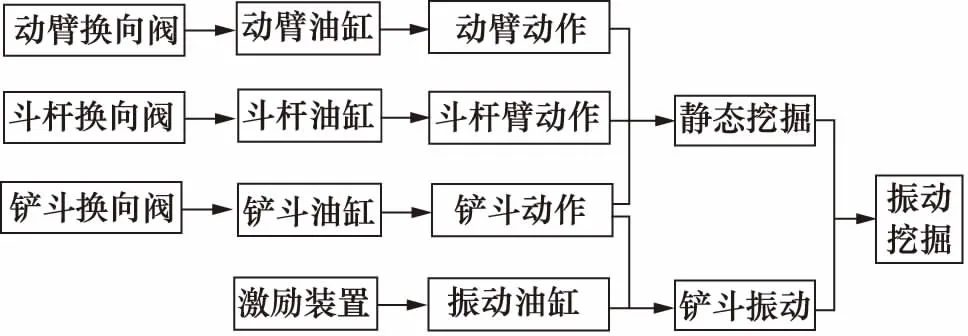
图2 振动实现方式原理图

2 振动挖掘试验

2.1 试验设备及系统组成

以1台1.5 t型的液压振动挖掘臂为实验设备，一套振动挖掘控制系统，按照振动挖掘机试验平台的设计结构和液压系统工作原理，以及振动挖掘试验条件要求，可以将整个智能控制系统分成三大组成模块，分别为检测模块、控制处理模块和动作输出模块。整体模块图如图3所示。

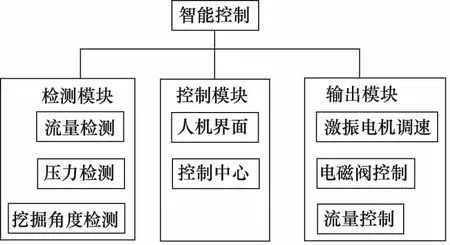
图3 总体控制方案模块图

2.2 试验方案

以福州地区普遍存在的黄性土壤振动试验挖掘对象，因试验主要考虑振动参数对液压振动挖掘的影响，土壤特性的差异性未纳入考虑范围。试验分别就振动频率、振动幅度、挖掘速度3个振动挖掘参数进行单因素挖掘试验，并在单因素试验结果的基础上，再对黄土以振动频率、振动幅度、挖掘速度为3个影响因子进行二次回归正交试验，采用Box-Behnken Design中心实验组合设计方案，如表1所示。最后以挖掘阻力为响应值进行响应面法分析，建立二次多项式数学模型并进行方差分析3个影响因子之间的交互作用，并得出相应土壤的最佳振动挖掘参数。

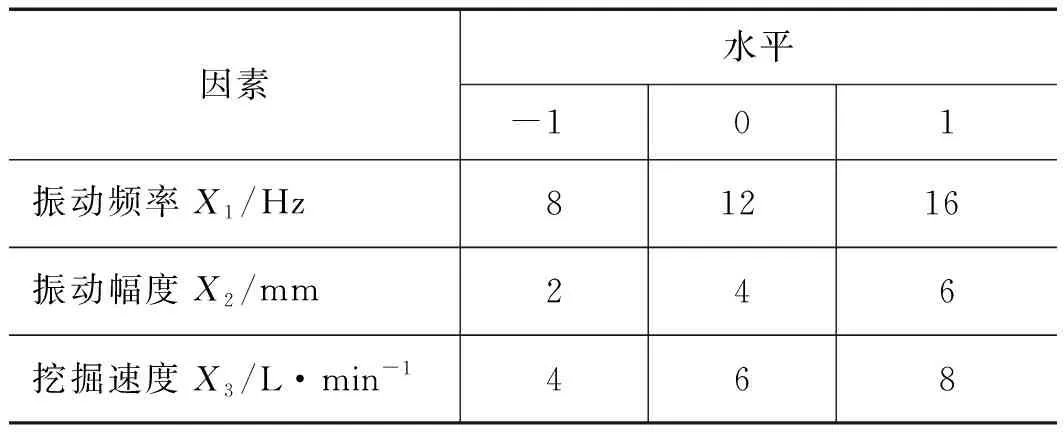
表1 Box-Behnken Design中心实验组合设计方案

3 试验结果与分析

3.1 单因素试验结果

1) 频率变化的单因素振动挖掘试验

振幅为3 mm，挖掘速度为6 L/min，频率为变化因素的单因素试验的结果数据如表2所示。

图4 液压振动挖掘试验图

表2 振动频率试验结果

2) 振幅变化的单因素振动挖掘试验

振动频率为12 Hz，挖掘速度为6 L/min，振幅为变化因素的单因素试验结果如表3所示。

表3 振动幅度试验数据结果

3) 挖掘速度变化的单因素振动挖掘试验

振动频率为12 Hz，振幅为3 mm，挖掘速度为变化因素的单因素试验结果如表4所示。

表4 挖掘速度试验结果

3.2 二次回归正交试验结果

根据Box-Behnken Design中心实验组合设计方案进行振动挖掘试验，得到结果如表5所示。

按照表5顺序进行挖掘试验得到挖掘阻力结果之后，应用Design Expert 8.0.6软件进行多元回归拟合分析，可以得到挖掘阻力Y关于振动频率X1、振动幅度X2、挖掘速度X3的真实值二次多项式响应面回归模型方程,为：

Y=4.23-0.16X1-0.39X2+0.28X3+0.16X1X2-

表5 黄土Box-Behnken试验设计结果

3.3 方差及响应面分析

根据二次多项式响应面回归模型，进行方差分析结果如表6所示。

由表6可以得出，通过拟合分析得到的真实值二次多项式响应面回归模型方程的P值远小于显著要求的数值，体现出非常显著的特性，且该模型方程的失拟项P值大于显著的要求数值，为非显著特性。因而该回归方程模型与试验得到的数据拟合较好，能够反应出真实中的3个因素与挖掘阻力之间的变化关系，可以利用该模型来分析和推导黄土的最佳振动挖掘参数。

由响应面分析软件进一步得到3个因素与挖掘阻力的响应曲面关系图和等高线关系图。如图5～图7所示，根据图中的三维曲面和等高线得出振动频率和振动幅度两个因素的交叉作用对挖掘阻力的影响大于其他组合因素的交叉作用影响，且3个因素对挖掘阻力的影响程度顺序为：第一振动幅度，其次挖掘速度最后为振动频率。结合前面的真实值二次多项式响应面回归模型，响应面分析特性以及软件计算分析，得出黄土的最佳振动挖掘参数是： 振动频率11.99 Hz， 振动幅度4.69 mm，挖掘速度4 L/min。此时挖掘阻力达到最小为4.018 MPa，根据所得到的最佳振动参数后再进行多次振动试验验证，得到的实际挖掘阻力值与模型得到的最小挖掘阻力值得偏差均在5%以内，在允许误差范围之内，得到的最佳振动参数具有一定可靠性。

表6 黄土振动挖掘的响应面二次方差分析表

注：**表示极显著(P<0.01)； *表示显著(P<0.05)。

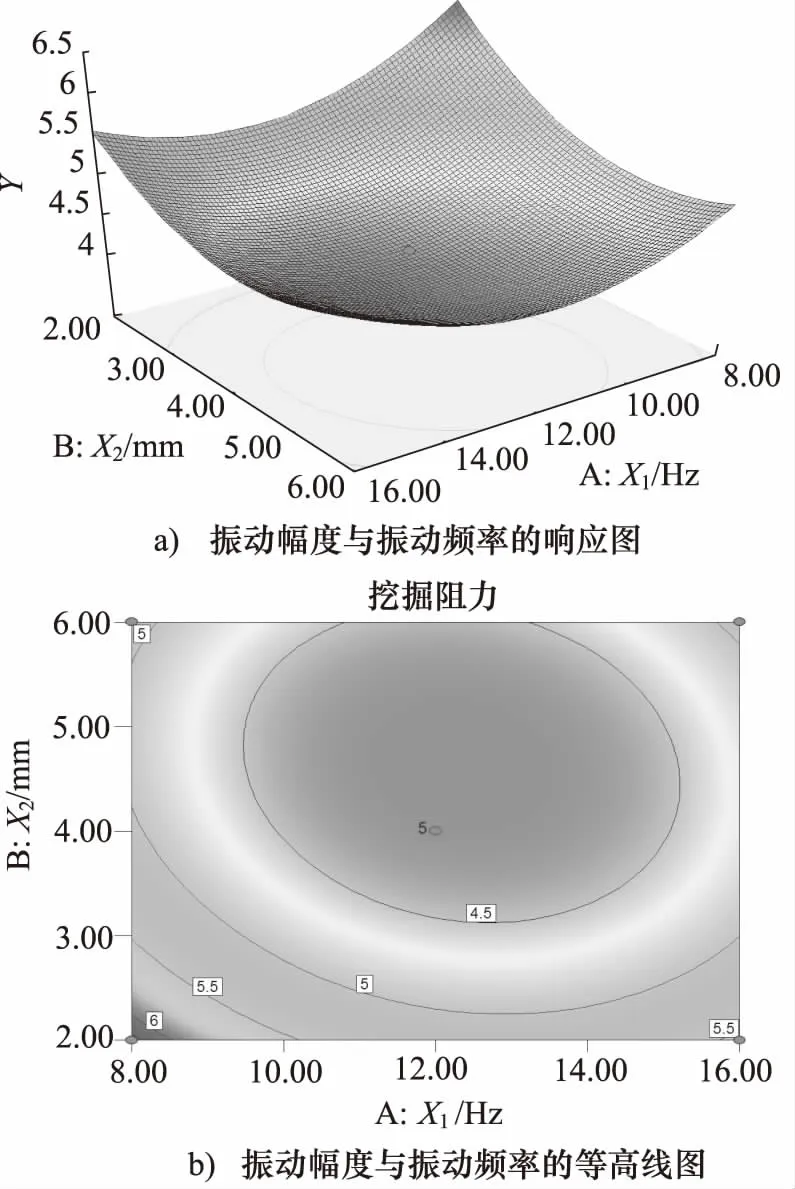
图5 振动幅度、振动频率与挖掘阻力关系图

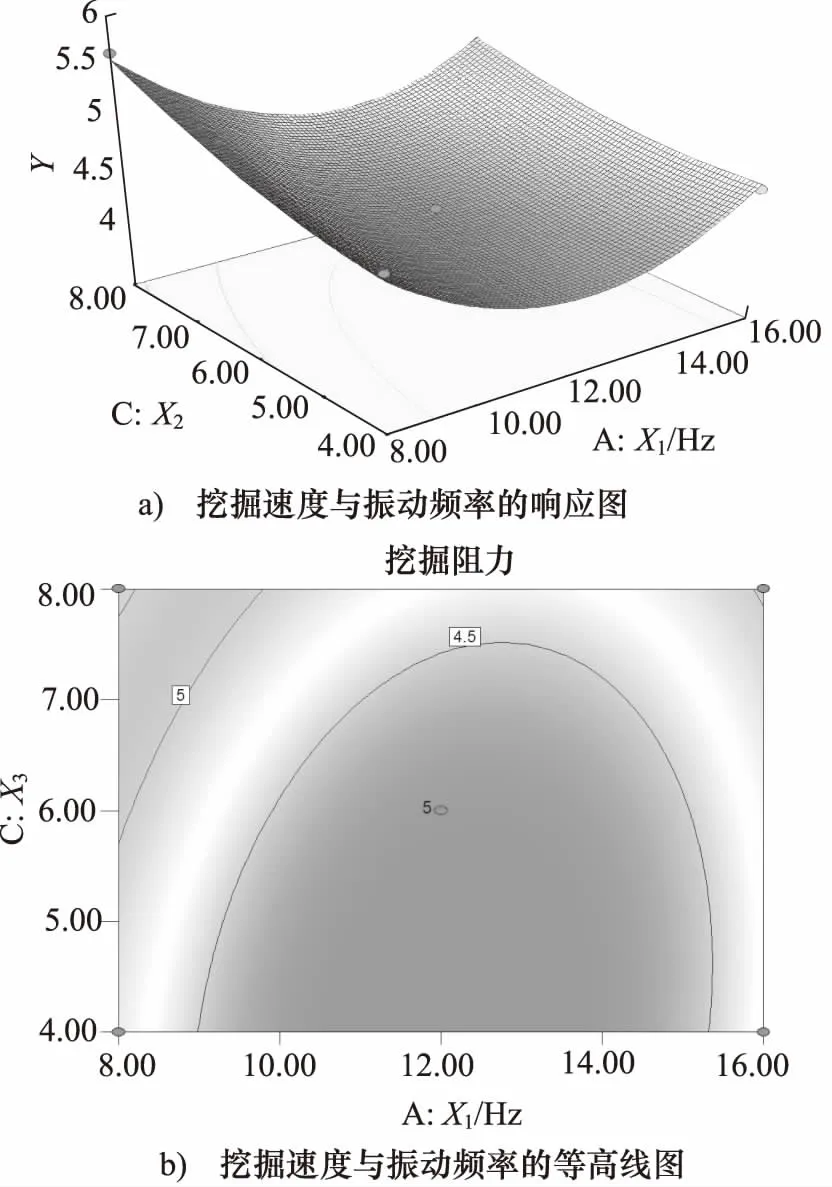
图6 挖掘速度、振动频率与挖掘阻力关系图

图7 挖掘速度、振动幅度与挖掘阻力关系图

4 结论

(1) 振动作用下进行对土壤的挖掘，能够有效的降低挖掘阻力，且振动频率在土壤的固体频率时的挖掘阻力最小，振幅的增大可以降低挖掘阻力，而挖掘速度的增大则会增加挖掘阻力；

(2) 对于黄土，3个振动因素对挖掘阻力的影响程度大小顺序为：振动幅度，其次为挖掘速度，最后为振动频率。同时得到黄土的最佳挖掘参数为：振动频率11.99 Hz，振动幅度4.69 mm，挖掘速度4 L/min。试验验证了振动参数对于液压振动挖掘的影响作用，对于其他土壤，比如砂土、红土等土壤也有推广作用。