两端铰接直线气缸弯曲振动研究
2020-05-22
(华南理工大学 机械与汽车工程学院, 广东 广州 510640)
引言
气缸作为工业自动化系统中非常重要的执行元件,被广泛地应用于各个工业设备生产制造的过程中,是实现工业自动化和气动技术广泛应用的关键零部件[1]。随着工业4.0和绿色制造理念的不断深入,人们对气缸的性能也提出了更多的要求[2]。在多年以来的可靠性试验研究中,发现气缸存在如下几种常见的失效模式:耐磨环与导向套的磨损,螺纹松动导致端盖破坏以及气缸偏磨损。因此有必要研究气缸的失效机理以及各因素对气缸内部接触力的影响,从而提高气缸的可靠性。一直以来,对于气缸内部以及活塞杆的分析大多集中在活塞轴向动力学研究上[3-4]。李飞等[5]针对气缸在轴向方向的冲击进行了有限元仿真分析。孙智权等[6]将活塞与端盖冲击过程中的接触介质等效为1个弹簧,对气缸活塞在行程末端的冲击过程建立解析模型。以上研究均未考虑活塞杆在运动过程中的弯曲振动问题。针对气缸的偏磨损现象,也无法得到有效的理论分析。
基于以上原因,本研究针对两端铰接固定的直线气缸进行动力学分析,将模型抽象为摆动导杆机构进行建模,得到气缸导向套与活塞杆,缸筒与耐磨环这2个关键部位接触力的解析表达式,并与有限元仿真数值解进行了对比,从而验证解析式的可靠性。另外,还通过灵敏度分析得到接触力与各影响因素之间的关系表达式,从而为减小气缸的内部接触力,提高气缸的可靠性提供了理论依据。
1 两端铰接固定气缸建模与解析
两端气缸铰接固定气缸在工业中应用广泛,在生产线、喷洒机构、起重器等生产设备上都有应用[7-11]。本研究将两端铰接固定气缸抽象为如图1所示的摆动导杆机构。
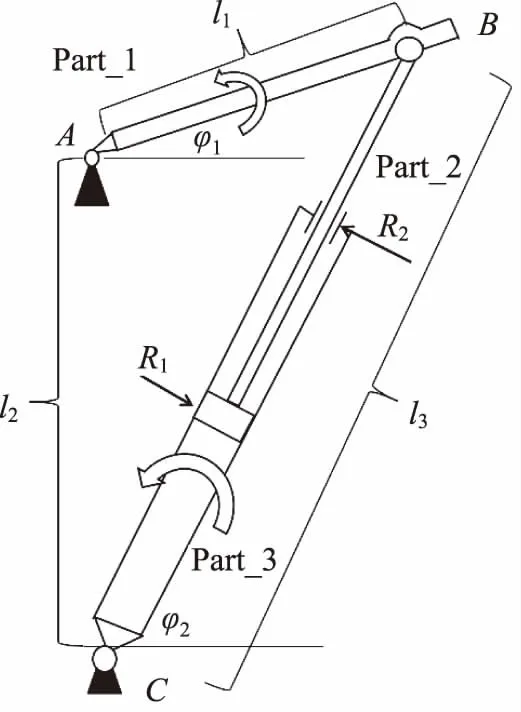
图1 两端铰接固定气缸模型
表1 基本技术参数
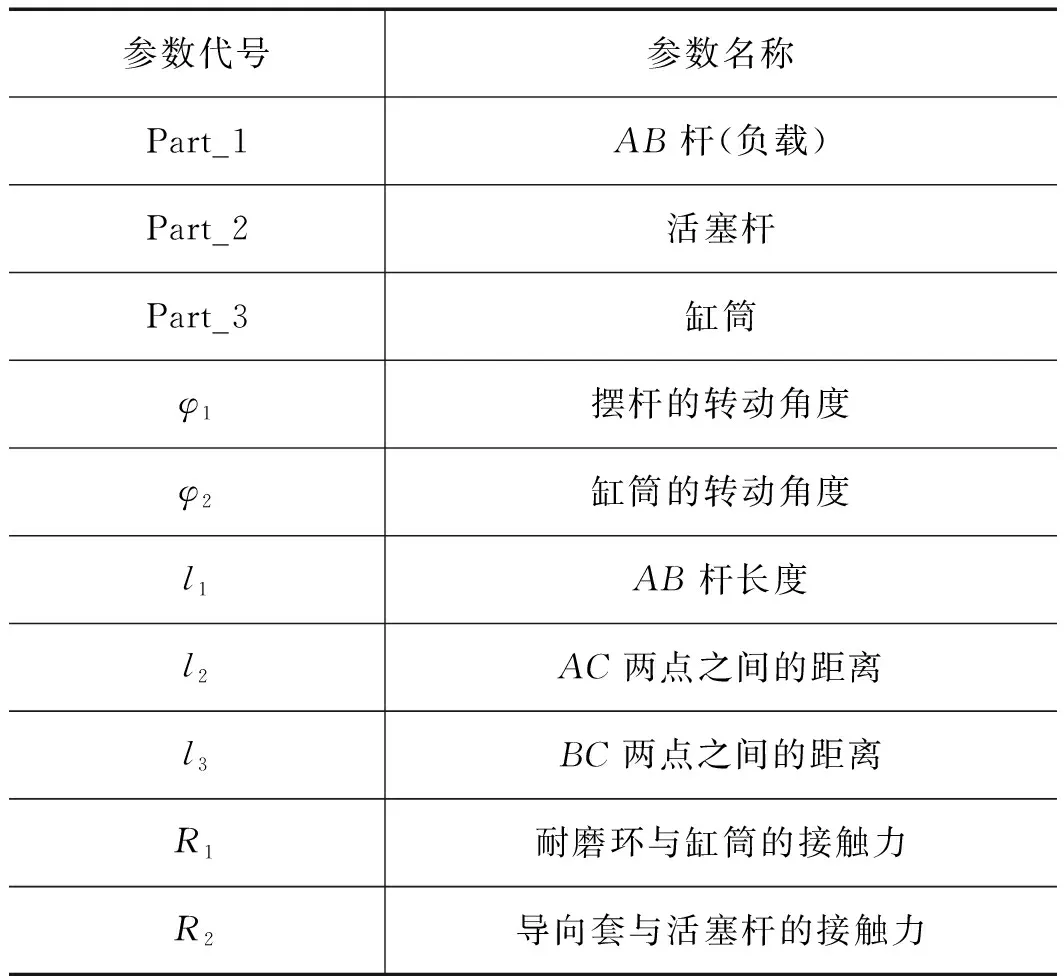
参数代号参数名称Part_1AB杆(负载)Part_2活塞杆Part_3缸筒φ1摆杆的转动角度φ2缸筒的转动角度l1AB杆长度l2AC两点之间的距离l3BC两点之间的距离R1耐磨环与缸筒的接触力R2导向套与活塞杆的接触力
本研究的气缸为标准型单杆双作用气缸,在对气缸系统进行数学建模时,为了便于简化分析,将气缸活塞杆假设为匀速运动。在气缸运动的过程中,计算图1中R1和R2随时间的变化关系。
1.1 运动学分析
假设图1中活塞杆的运动速度为v,可以得到图1中BC两点之间的距离为:
l3=l0+vt
(1)
式中,l0为整个机构未开始运动时,BC两点之间的长度。
图1中的ABC三点之间的距离可构成封闭三角形,通过余弦定理可以得到l1,l2,l3之间的关系。
(2)
(3)
式中,l1——AB杆长度
l2——AC两点之间的距离
l3——BC两点之间的距离
φ1—— 摆杆的转动角度
φ2—— 缸筒的转动角度
通过三角变换,可以求得φ1,φ2关于时间的表达式:
(4)
(5)

如图2所示为摆动导杆机构的运动学求解结果。
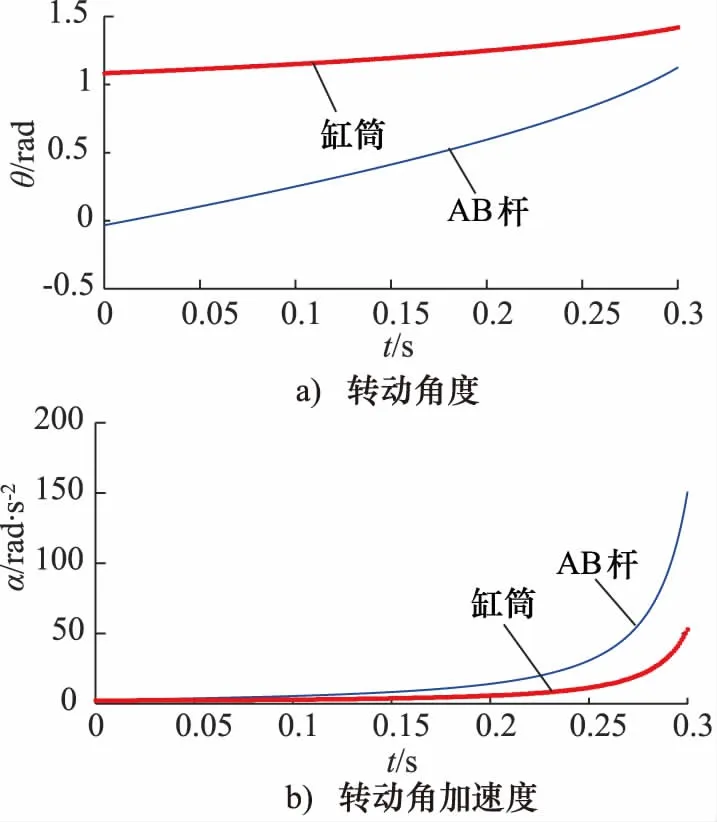
图2 运动学求解结果
1.2 动力学分析
为了求解出R1和R2随着时间的变化关系,可以将摆动导杆机构中的AB杆,缸筒,活塞杆分别进行受力分析。
AB杆的受力分析如图3所示。
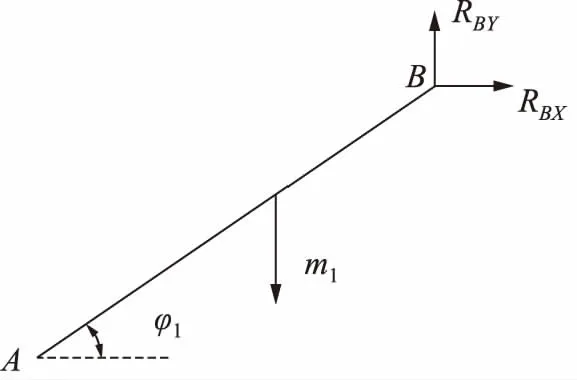
图3 AB杆受力分析
首先对于AB杆,它受到图3中B点的支撑力,在支撑力的作用下,AB杆绕A点做定轴转动,B点的支撑力可以分解为沿X轴和Y轴2个方向,在考虑重力的作用下,可以得到式(6):
(6)
式中,RBX—— 活塞杆在B点的力沿X轴的分量
RBY—— 活塞杆在B点的力沿Y轴的分量
m1——AB杆的质量
g—— 重力加速度
r1——AB杆的质心到A点的距离
J1——AB杆绕A点的转动惯量

活塞杆的受力分析如图4所示。

图4 活塞杆受力分析
对于活塞杆,受到气缸两腔气压形成的推力作用,活塞杆重力,活塞杆和缸筒两个接触位置的接触力以及B点的支撑力。
沿活塞杆轴向方向的受力使得活塞杆沿轴向运动,可以得到式(7):
(7)
式中,P—— 活塞杆受到的推力
m2—— 活塞杆的质量

受到垂直于杆轴向方向的力使得活塞杆随着缸筒一起绕C点做定轴转动,可以得到式(8):
RBX(l0+s)sinφ2-RBY(l0+s)cosφ2-
(8)
式中,s—— 活塞杆的伸出长度
d1,R2—— 作用点到C点的初始距离;
d2——R1作用点到C点的初始距离
r2—— 活塞杆的质心到C点的初始距离
J2—— 活塞杆C点的转动惯量

缸筒的受力分析如图5所示。
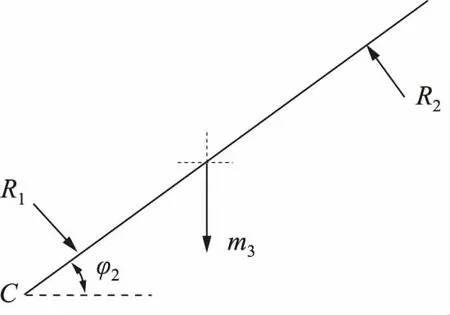
图5 缸筒受力分析
缸筒受到活塞杆与其的接触力作用以及自身的重力,绕C点做定轴转动。
(9)
式中,m3—— 缸筒的质量
r3—— 缸筒的质心到C点的距离
J3—— 缸筒绕C点的转动惯量
联立上述4个方程,可以得到摆动导杆机构接触力计算的解析模型:
(10)
2 基于ADAMS的动力学仿真分析
在ADAMS中建立摆动导杆机构模型的主要步骤如下:
(1) 在SOLIDWORKS中绘制摆动导杆机构的三维模型,将模型保存为.x_t格式并导入到ADAMS中;
(2) 根据机构实际使用材料定义各个零件的材料属性。相关零部件的材料属性如表3所示;
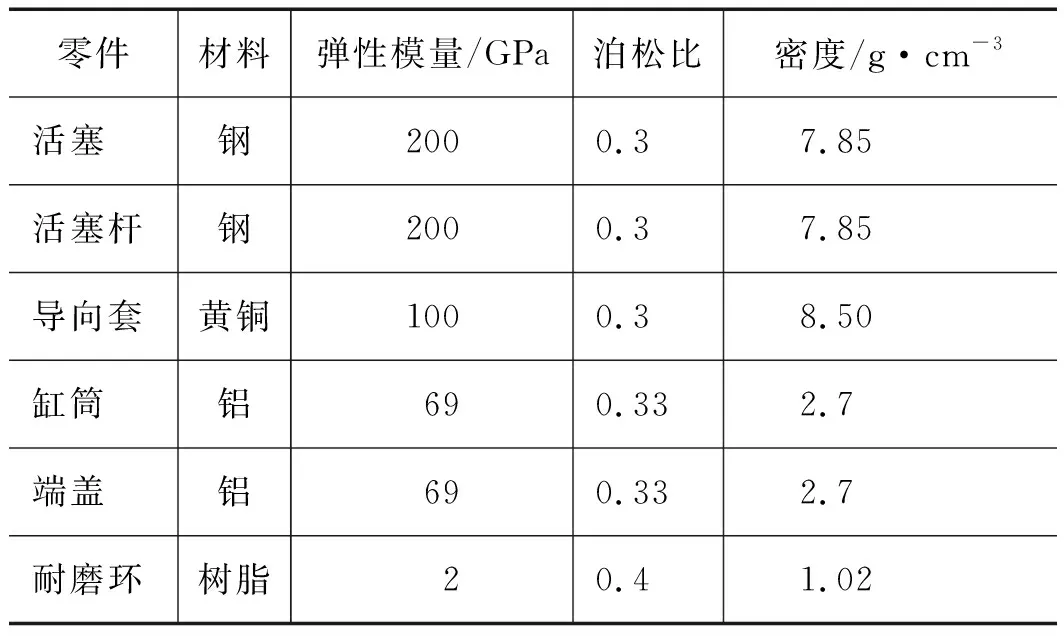
表3 相关零部件的材料属性
(3) 定义运动副如表4所示;
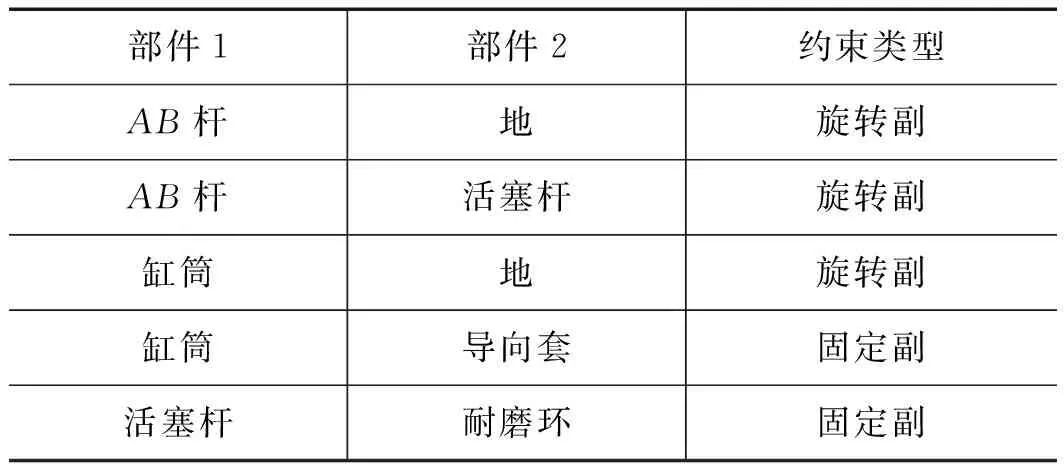
表4 运动部件运动副类型
(4) 定义碰撞接触副,ADAMS中采用冲击函数(IMPACT-FOUNCTION)定义2个部件之间接触关系,此次仿真主要考虑法向接触力,不考虑摩擦力作用;根据耐磨环与缸筒以及导向套与活塞杆之间的接触属性,定义啮合刚度、阻尼和贯穿深度等参数;
(5) 定义作用于活塞杆的驱动载荷,使活塞杆匀速运动;
(6) 定义求解器参数。因为活塞杆在受到上述负载驱动下走完单个行程需要0.3 s的时间,故设置总仿真为0.3 s,仿真总步数为1000步。
3 结果对比
针对气缸在弯曲振动情况下产生的内部接触力,通过动力学解析与ADAMS仿真得到的结果进行对比如图6、图7所示。
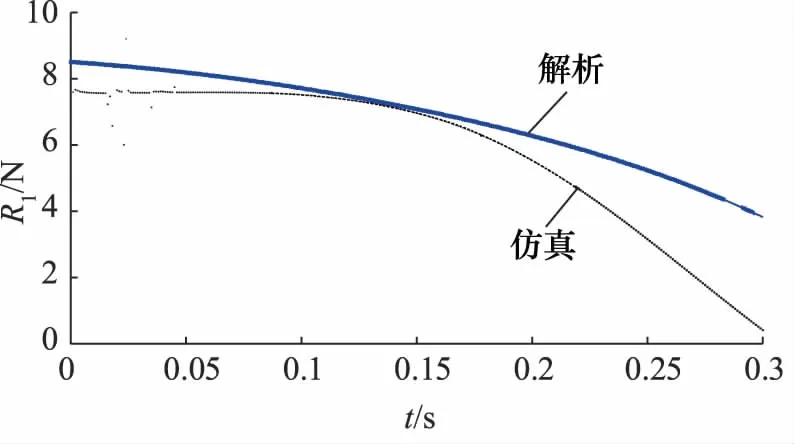
图6 活塞杆-导向套接触力

图7 缸筒-耐磨环接触力
通过上面的对比可以发现,通过动力学方程解析得到的接触力结果与ADAMS仿真得到的结果基本保持一致。从而验证了动力学解析解的正确性。
4 基于动力学解析方程的灵敏度分析
灵敏度分析的目的是获得负载质量、活塞杆质量、缸筒质量、气缸两腔气压、活塞杆伸出速度等因素对气缸内部接触力的贡献程度大小,为减小气缸内部接触力,提高气缸的可靠性提供理论依据,因此,可以将气缸内部的2个主要接触力作为因变量,将负载质量,活塞杆质量等模型参数作为自变量,利用蒙特卡洛方法和数据回归方法,找到其映射关系[12]。根据前面推导得到的摆动导杆机构动力学方程,可以得到各因素与内部两个接触力的多组对应数据,从而为正交试验提供数据。设有N次蒙特卡洛模拟,即有N组影响因素对应的接触力大小,利用数据回归方法便可以得到各影响因素与接触力之间的映射关系。
4.1 正交试验
本研究采用单一水平正交试验方法来进行接触力与各影响因素映射关系的实验。正交试验方案如表5所示。
4.2 灵敏度模型的建立
通过MATLAB编程计算得到不同的模型参数对应的接触力大小。对所有变量进行归一化处理以后,利用多元线性回归分析得到接触力与模型主要参数之间的映射关系如下所示:
R1=0.11m1+0.0814m2+0.172m3+
0.706P-0.193v
(11)
R2=0.352m1+0.382m2+0.283m3+
0.299P-0.129v
(12)
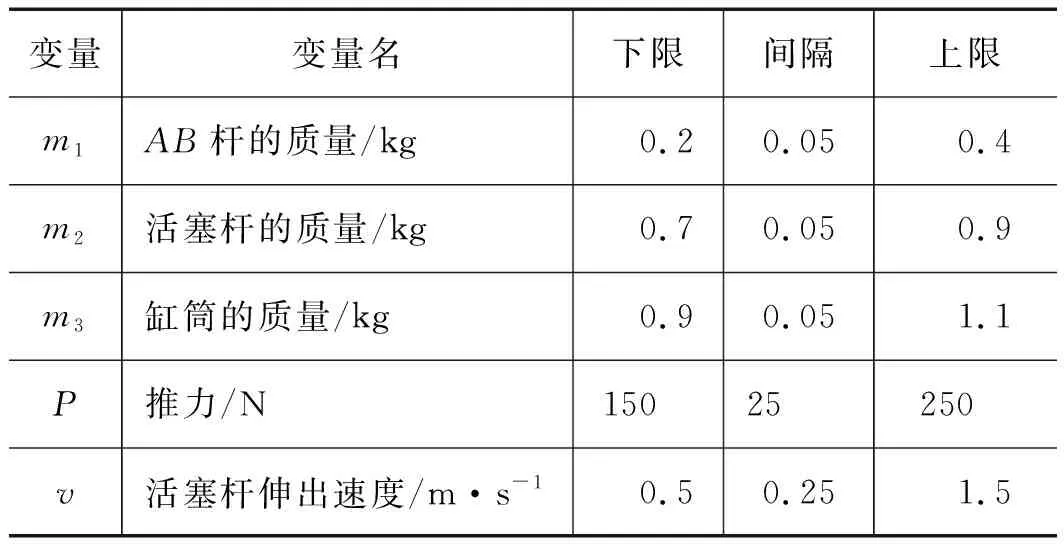
表5 正交试验方案
4.3 灵敏度分析结果
从图8、图9中可以看出,活塞杆与导向套的接触力受气缸两腔气压差以及缸筒质量的影响较大,而耐磨环与缸筒的接触力受活塞杆质量以及负载质量的影响较大。

图8 活塞杆-导向套接触力灵敏度分析

图9 耐磨环-缸筒接触力灵敏度分析
通过上述灵敏度分析结果可以发现气缸缸筒和活塞杆之间的接触力除了与气缸内气压、活塞速度有关外,与气缸质量也有很大关系,从某种角度讲,气缸轻量化设计有助于提高气缸使用寿命。
5 结论
本研究对两端铰接固定的直线气缸存在的弯曲振动现象进行动力学建模,将其抽象为1个摆动导杆机构,通过对机构中3个主要零件进行受力分析,得到气缸内部接触力的解析解,并且通过ADAMS动力学仿真,验证了解析模型的正确性。
在得到气缸内部接触力求解模型的基础之上,针对影响接触力的几个重要因素进行灵敏度分析,得到接触力与各影响因素之间的定量关系,研究结果为减小气缸内部的接触力从而提高气缸的可靠性提供了理论依据。
