一维近自由电子能谱的数值拟合与分析*

董艳杰，胡建民，王月媛，周 胜，牛丽

(哈尔滨师范大学)

0 引言

近自由电子近似法是求解固体能带结构的基本方法，也是固体物理教学的重点和难点．目前主流教材对近自由电子近似法的处理方式大体分为两种：其一是给出较为详尽的推论，但是过程冗长[1-2]；其二是较大幅度裁剪过程性推导和分析，只给出关键步骤和结论[3-4]，这种处理方式虽然简洁，但是基本模型的物理意义不够清晰明确．为此，该文对近自由电子非简并和简并能谱进行数值模拟，利用图示揭示近自由电子模型的内在物理意义，通过建立孤立原子、紧束缚电子、近自由电子模型的势能曲线变化示意图，对比分析紧束缚电子、近自由电子和空晶格电子模型之间的本质区别和内在联系，旨在为固体物理学习者和固体物理教学提供借鉴与参考．

1 非简并能谱数值分析

利用量子力学非简并微扰理论求解一维弱周期场中近自由电子能量为[5]

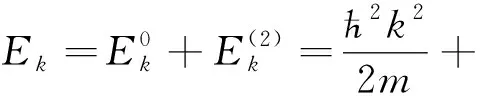
(1)

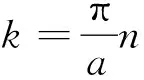
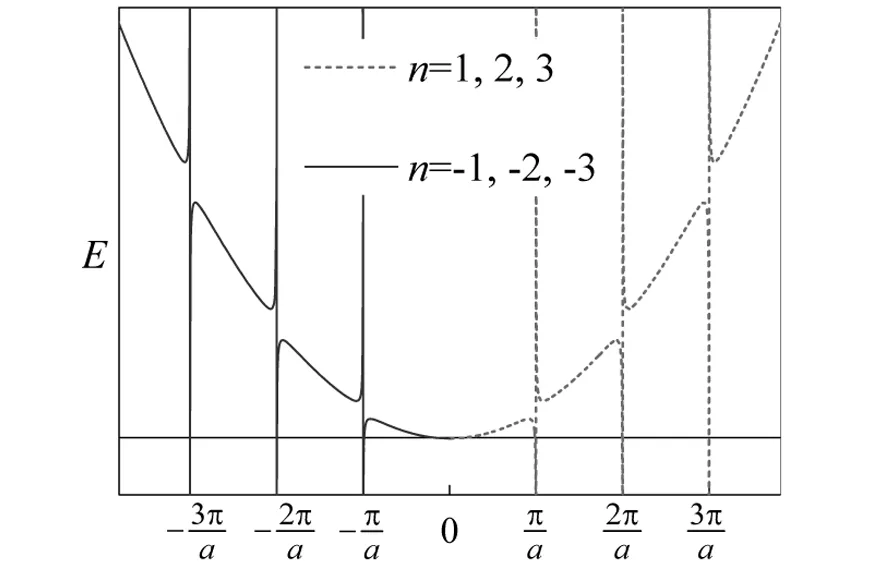
图1 非简并情况下一维晶格近自由电子能谱

2 简并能谱数值分析

在布里渊区边界附近电子处于简并态，采用简并微扰理论求解电子能量为[5]

(2)

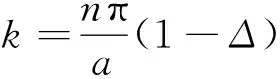
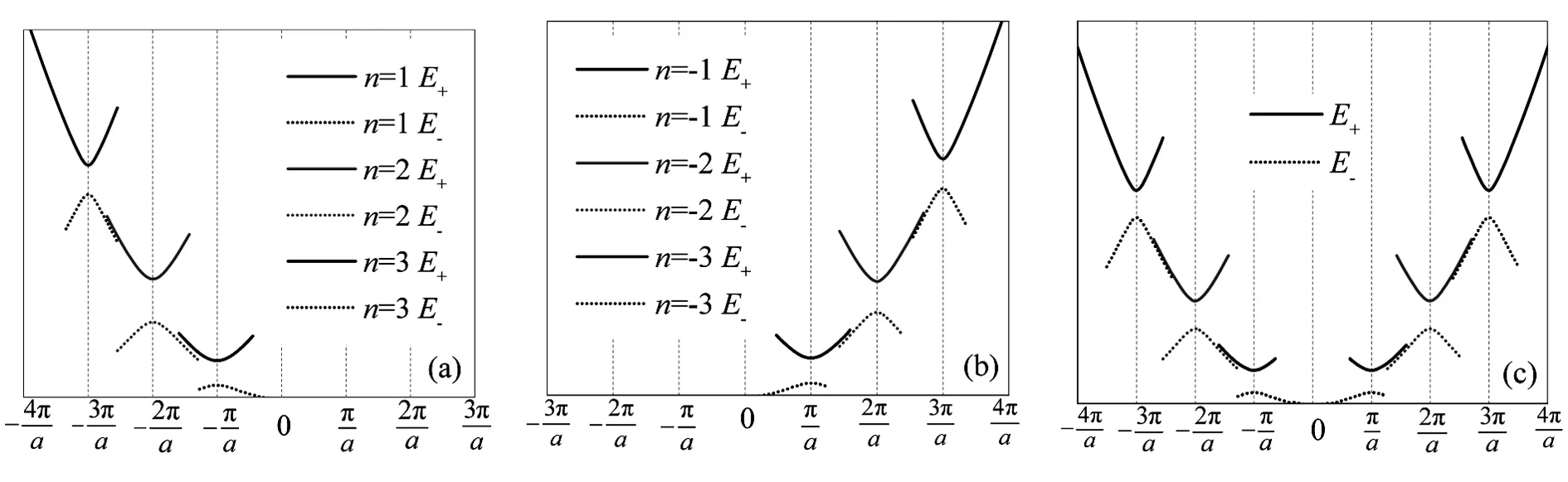
图2 简并情况下的一维晶格近自由电子能谱拟合过程

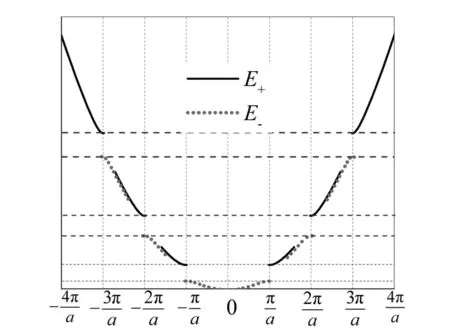
图3 一维晶格近自由电子能谱曲线

3 近自由电子和紧束缚电子模型

近自由电子模型和紧束缚电子模型即有本质区别又密切相关[7].紧束缚电子模型是由孤立原子模型随原子间距不断减小过渡而来的.在孤立原子中电子被完全束缚在原子核周围，原子势能变化如图4(a)所示，可见电子动能E远小于2个原子间的势垒高度从而原子间没有电子交换.当2个孤立原子间距逐渐减小但仍然远大于原子的限度时，电子受原子核的束缚相对于孤立原子变弱，由于原子核对电子的束缚仍然较紧，所以电子的状态波函数更多地保持孤立原子的特征，这就是紧束缚电子模型，其原子势能变化如图4(b)所示.由图4(b)可见，电子的动能接近势垒高度，从而电子以一定的几率穿越一定高度和厚度的势垒进而可以在2个原子间实现电子交换.对于原胞中只含有1个原子的简单晶体一般情况下原子间的相互作用使孤立原子的1个分立能级分裂成1个能带.紧束缚电子模型适用于原子间距较大的绝缘体或者半导体，例如金刚石是典型的绝缘体，而Si和Ge是典型的半导体，它们都是金刚石结构，原子堆积方式是松散堆积，致密度为0.34.

晶体的能带与禁带宽度强烈地依赖于原子间距和晶体结构.当孤立原子的间距逐渐减小并结合成晶体时，分别形成绝缘体、半导体和导体.随2个原子间距进一步减小，原子势场发生交叠导致原子间势垒宽度变薄和高度降低，当一维原子链中原子间距减小到与原子线度相差不多时，原子间势垒厚度很小高度很低，形成弱周期场，这就是近自由电子模型，如图4(c)所示．由图4(c)可见，电子动能远大于其在周期场中随空间位置变化的势能，这种情况下电子很容易越过势垒在晶体中运动而成为公有化电子．近自由电子模型适用于原子间相对靠近的金属晶体，原子间距较小使禁带消失导致能带发生交叠，例如碱土金属具有密排六方结构，原子相互靠近排列方式为密堆积，致密度为0.74.

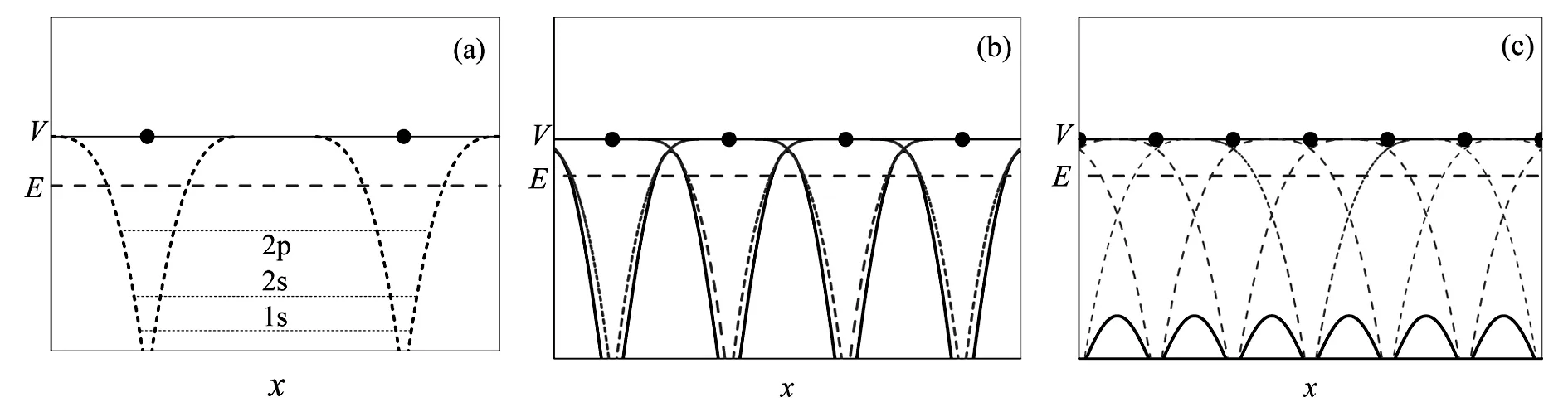
图4 一维晶体原子势能变化曲线示意图(a) 孤立原子模型； (b) 紧束缚电子模型； (c)近自由电子模型

当近自由电子模型中的弱周期场随空间位置的变化幅度逐渐减弱并过渡为常势场时有Vn→0，则布里渊区边界处禁带宽度逐渐变窄最后消失，而此时晶体的周期性结构仍然存在，电子在布里渊区边界处仍然发生布拉格反射.布拉格反射可以看作是电子与离子实之间发生的完全弹性碰撞，没有能量损失，入射波和反射波能量都等于自由电子能量，从而这种情况下的电子能谱同样可以用简约波矢来表示，这就是空晶格电子模型.空晶格电子模型与真空中的自由电子有本质区别，它可以准确描述金属中的索末菲自由电子，受晶格离子常势场作用，与晶格离子发生散射作用，其能谱具有周期性．

近自由电子模型适用于金属，而金属的晶体结构一般为密堆积方式(如Cu、Ag和Au等晶体面心立方结构，碱土金属为密排六方结构)，而紧束缚电子模型适用于绝缘体或半导体，绝缘体(如金刚石)和半导体(如Si和Ge)大多为是松散堆积方式.通过以上分析可知，晶体的能带交叠与禁带的变化不仅与晶体的原子间距有关，还与原子的电子结构有关，而电子结构决定其晶体结构.已有实验研究表明，绝缘体在超高压力的作用下，原子间距减小，导致能带发生交叠而变成导体.

4 结论

该文对固体物理学中的一维近自由电子非简并和简并能谱进行数值拟合，分析布里渊区边界处电子能谱的基本特征，通过图示分析孤立原子模型、紧束缚电子模型、近自由电子模型和空晶格电子模型的联系与区别．近自由电子非简并能谱数值分析表明，在布里渊区边界能谱曲线出现色散峰，电子能量发散，这说明非简并微扰理论失效，此时应使用简并微扰理论求解布里渊区边界处的电子能谱；近自由电子简并能谱数值分析表明，布里渊区中心附近电子能谱与自由电子能谱相近，布里渊区边界附近电子能谱按照抛物线变化，出现禁带.对比分析紧束缚电子模型、近自由电子模型和空晶格电子模型表明，晶体能带的交叠和禁带的变化与原子间距、晶体结构密切相关.