直径55mm芯样折断力与普通混凝土力学性能指标关系试验研究
2020-05-22黄从斌邰洪生罗居刚杨智
黄从斌,邰洪生,罗居刚,杨智
(1.安徽省(水利部淮河水利委员会)水利科学研究院,安徽 合肥 230088;2.安徽省水利工程病害防治工程技术研究中心,安徽 合肥 230088)
1 引言
目前混凝土结构已在我国大量使用,其混凝土强度也一致备受学界和工程界的关注,主要的检测方法为回弹法、钻芯法、超声——回弹综合法。其中,回弹法对于测试面要求较高,只能反映出表层混凝土强度,推定时其准确性很难保证[1];超声——回弹综合法由于材料易受材料特性、混凝土强度、钢筋配置等因素影响[1-2]会对小尺寸构建产生效果弱,且离散型较大。而采用小直径芯样抗折法检测结构混凝土强度可以有效弥补现有检测方法的不足,不仅是对现有检测技术的有效补充,也将填补现有检测技术的空白,可以提高工程质量检测评价的准确性和可靠性,进一步保障了工程质量和管理运行安全,具有极为广阔的工程应用前景和良好的社会经济效益,因而采用小直径芯样抗折法检测结构混凝土强度技术,值得进一步进行研究。
2 试验设计
本文设计并制作了C20、C30、C40和C50四个批次试件,均采用商品混凝土。预制试件尺寸为600mm×700mm×200mm的混凝土试件48块,用于钻取不同龄期(14d、28d、90d)直径为55m的混凝土抗折芯样,共计制作144组432个小直径芯样抗折试件。同时预留不同龄期不同强度等级的标准混凝土抗压、劈拉、抗折试件,用于混凝土力学性能试验。
3 试验原理
小直径抗折检测混凝土强度是一种通过大量的小直径芯样混凝土三点抗折试验和标准试件的普通混凝土力学性能试验,以小直径混凝土芯样折断力和标准试件混凝土力学性能试验结果,来拟合芯样折断力与标准混凝土试件强度相关关系,以推定混凝土强度的新方法[4]。首先利用钻机的薄壁钻头在结构上钻得一定长度的芯样,再利用液压千斤顶或其他外力将芯样沿横向折断,得到折断力;基于材料力学简支梁的受力原理,根据式(1)计算得到混凝土抗折强度力学性能指标。
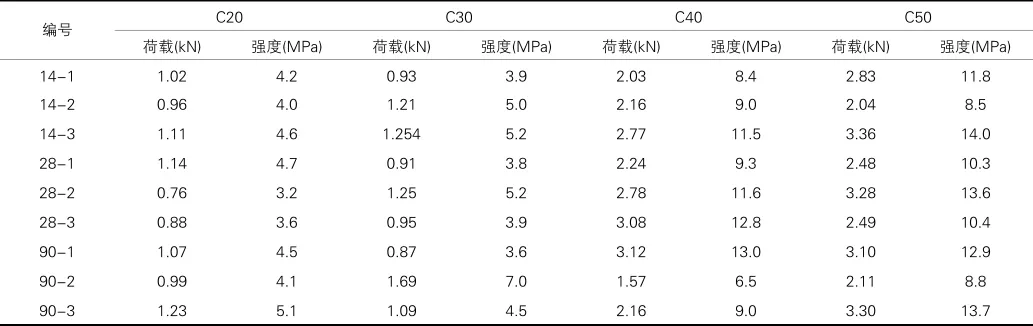
直径55mm芯样抗折力与抗压强度试验结果
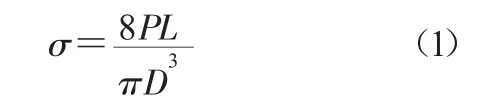
式中:σ—试件折断强度(MPa);
P—试件破坏时的折断力(kN);
L—试件两支撑间的支距(mm);
D—试件直径(mm);
4 试验数据分析
4.1 抗压强度相关关系分析
本试验采用小直径55mm芯样抗折试验机进行抗折试验,并测得标准试件的抗压强度如下表所示。表中编号14-1表示14天龄期,1号试件。由于版面篇幅有限,上表中仅提供部分数据。
对试验数据进行统计分析,以芯样折断力为自变量,标准抗压强度为因变量,回归曲线方程如图1所示。
通过上述图表可以看出:直径55mm芯样折断力与标准试件抗压强度的拟合函数中总体相关系数在0.8349~0.9079之间,相对误差在11.3%~18.2%之间,相对标准差在18.9%~26.4%之间。综合比较相关关系以及误差值,采用二次多项式函数来表达直径55mm芯样折断力—标准试件抗压强度关系曲线最佳。

图1 直径55mm芯样折断力—标准试件抗压强度关系曲线
4.2 抗折强度相关关系分析
不同强度等级、不同龄期的直径55mm芯样折断力及标准试件的抗折强度影响不同。同时,采用SPSS软件对试验数据进行统计分析,以芯样折断力为自变量,标准抗折强度为因变量,回归曲线方程如图2所示。
通过上述图表可以看出:直径55mm芯样折断力与标准试件抗折强度的拟合函数中总体相关系数在0.8954~0.9167之间,相对误差在8.6%~9.4%之间,相对标准差在15.6%~18.2%之间,综合比较相关关系以及误差值,线性函数的误差相对较小,采用线性函数来表达直径55mm芯样折断力—标准试件抗折强度关系曲线最佳。4.3劈拉强度相关关系分析
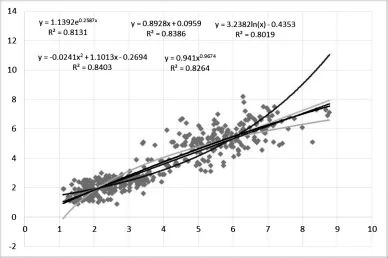
图2 直径55mm芯样折断力—标准试件抗折强度关系曲线
不同强度等级不同龄期的直径55mm芯样折断力及测得的劈拉强度有所不同。采用SPSS软件对试验数据进行统计分析,以芯样折断力为自变量,标准试件劈拉强度为因变量,回归曲线方程如图3所示。

图3 直径55mm芯样折断力—标准试件劈拉强度关系曲线
通过上述图表可以看出:直径55mm芯样折断力与标准试件劈拉强度的拟合函数中总体相关系数在0.8581~0.8940之间,相对误差在12.2%~14.8%之间,相对标准差在23.2%~29.7%之间,综合比较相关关系以及误差值,采用幂函数来表达直径55mm芯样折断力—标准试件劈拉强度关系曲线最佳。
5 结论
本文采用小直径芯样抗折法检测结构混凝土强度可以有效弥补现有检测方法的不足,不仅是对现有检测技术的有效补充,也将填补现有检测技术的空白,并根据试验数据取得以下结论:
①采用二次多项式函数来表达小直径55mm芯样折断力与标准试件抗压强度关系曲线最佳;
②采用线性函数来表达小直径55mm芯样折断力与标准试件抗折强度关系曲线最佳,相对误差较小;
③采用幂函数来表达小直径55mm芯样折断力与标准试件劈拉强度关系曲线最佳,相关性较好。
