一类低秩矩阵填充问题的快速优化算法*
2020-05-21郑伟东李声豪涂志辉胡文玉喻高航
郑伟东,李声豪,涂志辉,胡文玉,喻高航
(赣南师范大学 数学与计算机科学学院,江西 赣州 341000)
1 引言
矩阵填充(Matrix Completion, MC)问题主要解决得到数据矩阵的某一小部分的数据,填充那些未知或缺失的数据.为了解决这个问题,通常假设这个矩阵存在信息冗余,例如数据矩阵是低秩的,即其数据分布在一个低维的线性子空间上.目前,矩阵填充问题在推荐系统、图像恢复、数据分析以及机器学习等领域中有着广泛的应用.许多学者[1-8]在矩阵填充中做了大量的工作,这些工作主要围绕如下优化问题实现矩阵填充:

(1)
其中,X∈Rm×n是存在元素缺失的观测矩阵,A∶Rm×n→Rn是一个线性算子,b∈Rn.由于矩阵的秩函数是一个非凸且不连续的函数,因此,问题(1)是一个NP难问题.Candès和Recht[1]证明了问题(1)可以通过核范数近似矩阵的秩进行求解:

(2)


(3)
其中,δ≥0是噪声水平.另一方面,问题(3)还可以转化为如下的无约束的最小二乘问题:
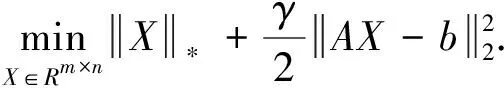
(4)

Micchelli等人[13]提出了基于临近算子的不动点算法,该算法在理论上可以解决两个凸函数相加的优化问题. 基于这种动机, 本文将问题(2)、(3)和(4)统一的归纳为两个凸函数相加的模型,使得求解该类矩阵填充问题时更加通用简洁.考虑如下模型:
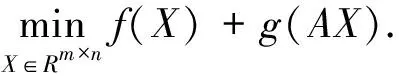
(5)
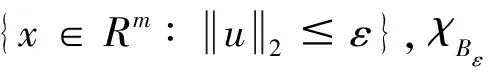

(6)
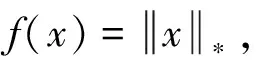
2 算法
为了进一步提高算法的效率,本节使用了临近算子并结合了临近算子和次微分之间的关系,提出了一类不动点算法来解决问题(5).
2.1 相关理论
首先给出临近算子和次微分的定义,并给出它们之间的联系和后续需要使用的一些性质.
定义1[13](临近算子)若f是Rm上的实凸函数,则函数f在x∈Rn的临近算子如下:

(7)


(8)
定义2[13](次微分)若f是Rm上的实凸函数,则函数f在x∈Rn的次微分如下:
∂f(x)={y∈Rn∶f(z)≥f(x)+〈y,z-x〉,z∈Rn}.
(9)
次微分是函数在不可微情形下的推广.若函数可微,则次微分就是函数的导数.由定义容易证明:λ∂f(x)=∂λf(x),其中λ≥0.
引理1[15]设f*是f的共轭函数,即f*(y)∶= sup{〈x,y〉-f(x)}.若x∈domf,y∈domf*,则
y∈∂f(x)⟺∂f*(y)∈x
(10)
成立.
引理2[13-14]若f是Rn上的一个凸函数,且x∈Rn,则对任意的H∈S+,有
Hy∈∂f(x)⟺x=proxf,H(x+y).
(11)
2.2 不动点算法
本小结设计求解优化问题(5)的不动点算法.假设X∈Rm×n是问题的最优解,则根据费马定理和链式法则,可得:
0∈∂f(X)+A*∂g(AX).
(12)
其中A*表示线性算子A的共轭算子.因此,存在y∈∂g(AX),使得0∈∂f(X)+A*y.由引理1和(12),可得:
AX∈∂g(y), -A*y∈∂f(X).
(13)
则对任意的矩阵P∈X+和Q∈S+,有
PP-1AX∈∂g*(y), -QQ-1A*y∈∂f(X).
(14)
根据引理2,可得如下与问题(5)等价的不动点方程组:
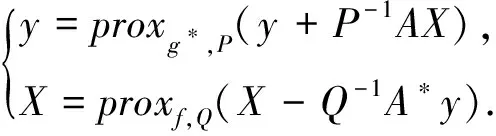
(15)
根据不动点方程组(15),可以设计不同迭代格式的迭代方法,如

(16)
虽然迭代格式(16)简单,且是显式的,但是算法可能不收敛[14].因此本文将构造一个半隐式迭代格式.对m个向量空间E1,E2,…,Em,定义向量空间Ei的内积为〈·,·〉Ei,且在笛卡尔积的内积空间定义如下[16]:

(17)

proxΦ,R(Z)=(proxg*,P(y),proxf,Q(X))⟹Zk+1=proxΦ,R(EZk),
(18)

Zk+1=proxΦ,R(E0Zk+1+E1Zk),
(19)
即

(20)
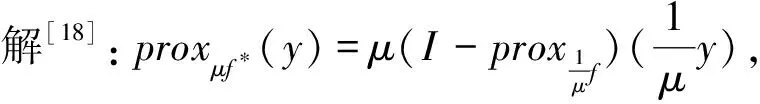

(21)
2.3 子问题求解
在问题的求解过程中,需要求解函数的临近算子.接下来将详细说明子问题的求解.
子问题yk+1对于有约束和无约束优化问题,计算g(x)的临近算子,分两种情况讨论.
因此,根据g(x)的临近算子容易求得yk+1.
子问题Xk+1给定值为r的矩阵X∈Rm×n,其奇异值分解为:X=Udiag(max{σi}1≤i≤r)VT,对任意的τ≥0,收缩奇异值阈值算子Dτ定义为:Dτ(X)=Udiag(max{σi-τ,0})VT.
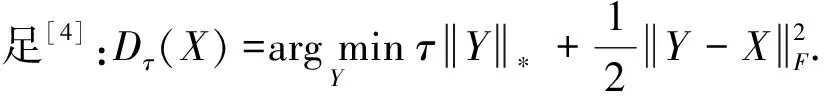

(22)
3 收敛性分析
本节将证明本文提出的不动点算法(20)是收敛的.
引理3[18]若f是从Rn到(-∞,+∞]的真下半连续(Proper lower semi-continuous)凸函数的集合,则proxf和I-proxf是扩张的.


〈Zk+1-Z*,R(E0Zk+1+E1Z*-Zk+1)-R(EZ*-Z*)〉≥0
⟺-〈Zk+1-Z*,RE1(Zk+1-Z*)〉+〈Zk+1-Z*,R(E-I)(Zk+1-Z*)〉≥0.

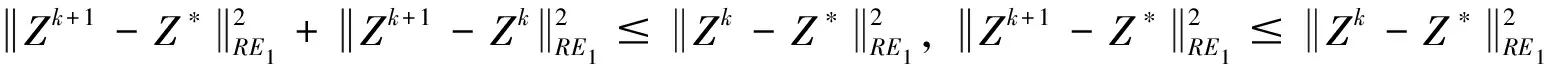

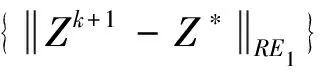


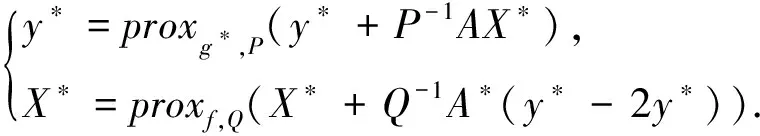
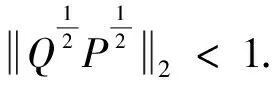
4 数值实验
在本节中,我们创建随机矩阵和样本集,然后使用我们的算法来解决无噪声矩阵填充问题、噪声矩阵填充问题和低秩图像恢复问题.同时将我们的算法与前面提到的ADMM[7]、IADM-CG[8]和IADM-BB[11]算法进行比较.所有的实验代码在MATLAB R2016上编写,以及在2.4GHz的主频CPU和4 GB的内存的计算机环境下运行.
部分奇异值计算计算Xk+1时,注意到在每次迭代过程中,需要计算奇异值分解(SVD). 但是,实际上只需要比阈值1/μ更大的奇异值.因此可以通过使用软件包PROPACK[19]来计算矩阵的部分奇异值分解,该软件用于计算大于阈值的奇异值和相应的奇异值向量.虽然PROPACK可以计算固定数量的奇异值,但它无法自动确定大于1/μ的奇异值的数量. 因此,为了执行部分SVD,我们需要预测每次迭代中大于阈值的奇异值的数量,具体更新规则如下:
其中svk表示预测的奇异值和奇异值向量的数量,sv0=min(m,n)×0.01,svpk是Xk的正奇异值的数量.
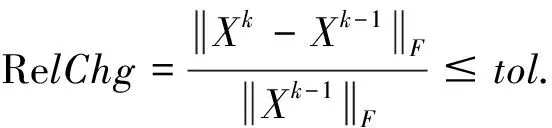
4.1 矩阵填充问题
在矩阵填充问题中,线性映射A是一个线性投影算子:AX=XΩ,XΩ是矩阵X的成分组成的向量形式.实验过程中,我们将根据三元组{m,r,p/dr}随机生成方阵M,其中m是矩阵的维数,r表示矩阵的秩,p为采样元素的数目,dr=r×(m+n-r)为m×n矩阵的自由度,同时定义样本采样率sr=p/(mn).首先生成每个元素为独立高斯随机变量的矩阵L=randn(m,r)和R=randn(n,r),然后计算M=LRT,接着均匀采样矩阵的p个元素.

表1给出的是本文提出的模型和算法与ADM和IADM-CG求解无噪声矩阵填充问题的数值实验结果,和噪声矩阵填充问题的数值结果,表2是使用本文的模型和ADM[7]、IADM-CG[12]算法求解有噪声矩阵填充问题的实验结果.从表中可以看出,本文的算法在精确度和计算效率方面优于IADM-CG算法,与ADMM算法相比计算效率相当,但本文的算法在精确度上具有优势.

表1 本文算法与ADM、IADM-CG算法求解无噪声的矩阵填充问题(Time:s)

表2 本文算法与ADM、IADM-CG算法求解有噪声的矩阵填充问题(Time:s)
4.2 低秩图像恢复中的应用
在本节中,我们使用最小二乘问题模型来对低秩图像进行恢复.通过测试512×512灰度图像(lena, pirate, cameraman)来验证本文的方法在实际应用中的有效性.首先,通过奇异值分解将原始图像压缩为秩为40的低秩图像.然后从低秩矩阵中随机获取一部分元素得到数据丢失的图像.最后,使用本文的模型和算法进行恢复.当RelChg低于tol=10-6或迭代步数大于1 000时,迭代过程停止.原始图像、低秩图像、数据丢失的图像和恢复的图像在图1中列出.从恢复的图像结果中可以看出,我们的模型和算法对于低秩图像的恢复是有效的.

图1 第一列:原始图像;第二列:秩为40的图像;第三列:采样率为sr=0.4的图像;最后一列:恢复图像
我们通过计算各方法的峰值信噪比(PSNR)来更好的比较恢复图像的效果,定义如下:
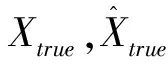
表3给出了通过不同的方法恢复秩为40的图像lena的时间、相对误差和PSNR.从表3可以看出,对于不同的采样率,本文的方法与ADM方法的PSNR比IADM-CG方法要好,即恢复的图像质量更好,并且本文方法的优势在于所需时间比其它两种方法较快许多.

表3 本文算法与ADM、IADM-CG算法对于低秩图像恢复(lena)
通过图2描述了恢复图像秩的估计与迭代步数的关系,以及相对误差与算法所用时间的关系.由左图可知,本文的方法在35次迭代之后非常接近真实的秩,由右图可知,本文的方法收敛速率更快.

图2 左图:秩的估计;右图:收敛速率
5 结语
本文归纳了基于核范数的矩阵填充模型,提出了一个统一的数学模型,并采用不动点算法求解该模型,使得迭代格式变得通用和简单, 且具有简洁的收敛性证明.在合成数据的矩阵填充数值实验中,本文的方法提高了算法的性能;在低秩图像恢复中,节省了大量的运行时间;并且对于相同模型不同的线性算子,算法框架也将适用,可应用于求解其它问题.
