中压配电网三相可信量测优化配置

刘 超，王旭东，苏彦卓，丁 一，王 尧，田家辉

(1. 国家电网天津市电力公司城东供电分公司，天津 300250； 2. 国家电网天津市电力公司电力科学研究院，天津 300201；3. 河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室，天津 300401)

近年来，配电网发展越来越受到重视，未来的主动配电网将更可靠、更灵活、更高效[1]。在主动配电网中，用户与电网互动频繁，控制中心需要及时掌握用户的用电信息；此外，大量具有间歇性和不确定性特征的分布式电源、电动汽车不断接入，增加了配电网中的不确定性因素。为了保证系统能够安全、可靠的运行，控制中心需要掌握更加准确的电网状态信息，以便对配电网进行及时控制和精细化管理，规避可能出现的风险，提高运行效率。在配电网中应用状态估计，可实时计算系统当前时刻的运行状态，为控制中心运行决策提供完整、可靠的数据，是感知系统实时状态的有效手段。

当前的配电网量测配置难以实现规模大、线路多的配电网状态估计。虽然当前配电网中安装了大量的智能电表[2]，获取的负荷与发电数据可以作为伪量测参与状态估计；但过度依赖伪量测将导致状态估计精度较差，因此必须配置一定数量的实时量测。由于要考虑经济性因素，无法实现在规模巨大的配电网中安装大量量测仪表，因此，有策略地对可信量测类型、位置、数量进行优化配置，使状态估计达到最高精度具有重要意义。

当前国内外关于中压配电网可信量测的优化配置的研究已有许多成果。文献[3]中就量测安置位置及类型对状态估计的精度影响的问题进行分析，给出量测配置的一般准则。基于这一准则，采用广义Moore-Penrose(简称M-P)逆等算法，文献[4]中推导了关于量测残差与状态估计误差间的数学表达式，从而给出量测评估及优化配置的方法。文献[5]中通过依次补充量测进行蒙特卡洛仿真，满足节点电压相角、幅值的状态估计精度，从而提出了一种序贯式的量测优化配置方法。文献[6]中将序优化的方法应用于量测配置中，结果显示能够得到比文献[5]中更优的解，然而该算法的求解时间长达数小时。文献[7-11]中考虑了网络参数不确定性、量测中断、网络重构等复杂工况，提出了量测仪表的鲁棒配置算法。文献[12]中研究了独立分量分析和配网先验信息进行谐波状态估计量测点优化配置。文献[13-14]中分别提出了配电网同步相量测量单元优化配置的分段迭代法和免疫离散粒子群算法。文献[15]中建立了配电网三相鲁棒量测优化配置模型，以保证当某一个量测缺失时网络仍然可观测。

虽然以上方法对于量测配置问题各有其特点和效果，但是普遍较为费时，且均为单相方法。本文中提出一种普遍适用于中压配电网的三相可信量测优化配置方法。首先，以三相状态估计误差总方差作为状态估计精度指标，建立三相可信量测优化配置模型；其次，通过Cholesky分解将目标函数采用决策变量显式表达出来，从而可调用成熟的优化软件实现快速求解；通过对13节点和37节点配电系统标准算列的改进和仿真测试，验证本文中所提算法的有效性和快速性。

1 支路电流作状态变量的配电网三相状态估计

1.1 量测模型

选择基于支路电流的配电网三相状态估计方法[3]，以实现雅可比矩阵三相解耦。基于支路电流的配电网三相状态估计采用三相配电线路模型(如图1所示)。

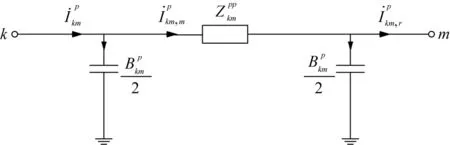
支路k-m的p相复电流(p为相别a、b或c)； 相复电流在线路中间、末端的分量； 支路k-m的p相自阻抗； 支路k-m的p相对地电导。图1 三相配电线路等效模型

(1)

(2)

量测方程为

z=h(x)+v，

(3)

式中：z为量测向量；x=[I1,I2, …,In,α1,α2，…,αn]T为2n维状态向量(n条支路的电流幅值和相角)；h(·)为非线性的量测函数；v为量测误差向量。

具体计算过程如下。

1)支路功率量测方程为

(4)

2)电流幅值量测直接对应其状态变量，因此无需电流幅值量测方程；

3)节点k电压幅值量测方程由根节点电压减去根节点到节点k间线路电压降所得，

(5)

(6)

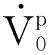
4)负荷量测方程为

(7)

式中：1～m为节点k的上游节点；(m+1)～n为节点k的下游节点。

1.2 估计模型

加权最小二乘估计准则为

J(x)=[z-h(x)]TR-1[z-h(x)]。

(8)

通过高斯-牛顿方法求解，得到正规方程

G(xk)Δxk=HT(xk)R-1[z-h(xk)]，

(9)

式中：G(xk)=HT(xk)R-1h(xk)为增益矩阵； Δxk=xk+1-xk；H(x)=∂h(x)/∂x为量测雅可比矩阵；R为量测误差协方差矩阵。增益矩阵的逆G-1(x)即为状态估计误差的协方差矩阵，它的对角元素是状态估计误差方差的Cramér-Rao下界，该矩阵的迹称为状态估计误差总方差(total variance of state estimation error, TVSEE)，是评价状态估计精度的重要指标。

2 三相可信量测优化配置

2.1 建模思路

某一时刻系统所有负荷节点的负荷决定了系统该时刻的真实运行状态。该时刻下，所有可能的可观测量测配置方案经加权最小二乘(WLS)法的状态估计结果，都是真实运行状态的无偏估计。因此，用蒙特卡洛方法进行仿真，不同的量测配置方案之间状态估计误差的数学期望值相同，但误差总方差不同。设系统在某一时刻t有真实状态y(t)，存在2种不同量测配置方案M1、M2，分别对应估计状态y1(t)和y2(t)，假设M1的估计精度高于M2的，则有

(10)

式中：确E(·)为系统状态的期望；σ(·)为状态估计误差总方差。

在不同时刻，虽然系统的真实运行状态随时间的变化而变化，但是并不影响量测配置方案的估计精度比较，即在其余时刻，方案M1的估计精度仍高于M2的。基于这种猜想，本文中在任意一致的系统真实运行状态下，寻找能使误差总方差达到最小的量测配置方案。

2.2 量测优化配置数学模型

将所有量测分为以下2类。

1)基本量测。由电表计费系统固定时限记录的电表数据或负荷预测数据和复合估计数据构成基本的伪参量。为了保证增益矩阵的正定性和网络的可观测性，伪参量赋予的权重较小，以减小其实时性差、精度低等因素对估计精度的影响。基本量测对应的雅克比矩阵设为HB，量测误差协方差矩阵设为RB，则增益矩阵为

(11)

2)候选量测。以所有可能配置的实时可信量测作为候选量测。对于三相不对称辐射状配电网，除根节点电压幅值量测外，具有np个节点、np-1条支路的p相网络，每相可配置共计3(np-1)个实时可信量测，其中包含电流幅值量测、支路功率量测、电压幅值量测的数量各有np-1个。

设候选量测雅可比阵为HM。实时量测权重与决策变量的乘积作为新的量测误差协方差，并形成每相量测误差协方差矩阵

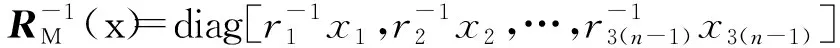
(12)

为了简化书写，省略相位下标p。当量测系统不含有某一个量测时，该量测对应权重即为0。

每相增益矩阵为

(13)

量测配置模型为

(14)

s.t.na(xa)+nb(xb)+nc(xc)=NM，

(15)

式中：NM为设定量测数目；向量x为0-1规划决策变量。支路电流状态向量可以取作系统任一运行点对应支路复电流。

2.3 模型求解

对于G(x)的求逆分2步执行：1)进行矩阵的Cholesky分解，即G(x)=LT(x)L(x)； 2)分别对2个三角矩阵LT(x)与L(x)求逆。

N维对称正定矩阵的Cholesky分解过程如下：

(16)

式中j=i+1,i+2,…,N-1。

按顺序i=1, 2，…，N执行上式，可将三角矩阵LT(x)与L(x)的逆矩阵元素通过决策变量x表示出来。

整体求解流程如图2所示。

TVSEE—状态估计误差总方差。图2 三相可信量测优化配置求解流程

3 仿真测试

模型采用C++编程调用LocalSolver 8.0[16]进行求解。LocalSolver是一款非线性规划软件，基于局部搜索启发式优化，能够较好地求解大规模混合整数非线性及组合优化问题，在求解MIPLIB 2010测试库中的一些难题时表现出比Cplex和Gurobi优化器更快的速度和更高的优化质量。美国电气和电子工程师协会(IEEE)提供了不同节点的配点系统标准算例，本文中对改进的IEEE 13节点和IEEE 37节点标准算例[17]进行仿真测试。

3.1 改进的IEEE 13节点配电网测试

改进的IEEE 13节点配电系统标准算例接线图如图3所示，数字为节点编号。该算例三相不平衡。表1列出了各相支路节点数目以及可配置的实时量测总数。

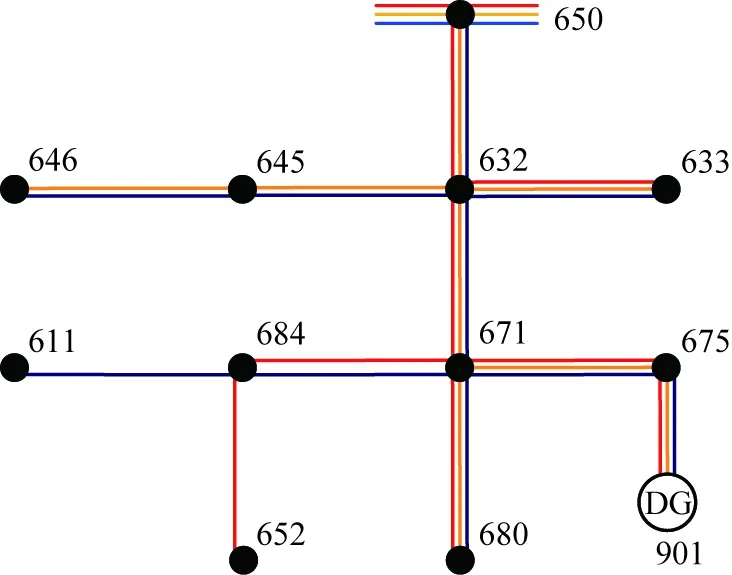
数字标号—节点代号； DG—分布式电源。图3 改进的13节点配电系统标准算例接线图

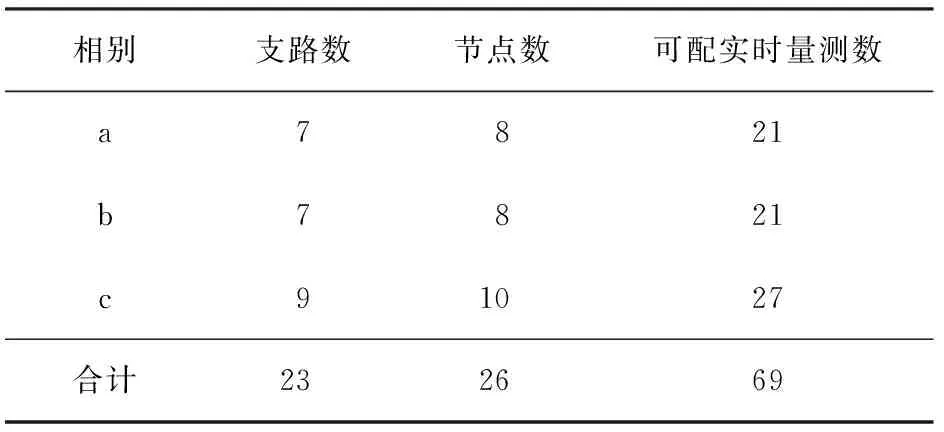
表1 改进的13节点配电系统标准算例参数

设定量测数量NM为1～69，每次计算时间设定为1 min，以计算不同量测数量的最优配置方案。TVSEE随NM变化曲线如图4所示，表2给出了NM为1～5的结果。在量测配置结果中，只出现支路功率量测，此阶段TVSEE随支路功率量测数量增加而迅速减小；NM为24时，出现支路电流幅值量测；NM为47时，出现节点电压幅值量测，但TVSEE不变。

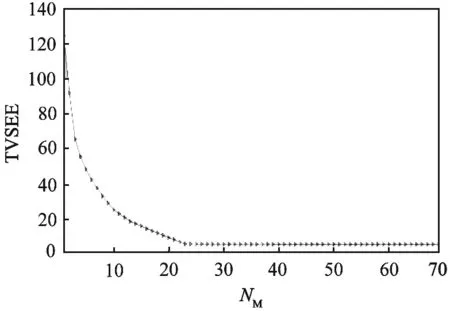
图4 改进的13节点配电网状态估计误差总方差(TVSEE)随实时量测装置配置数NM的变化曲线

由于支路功率量测包含幅值和相角，而支路电流幅值量测只包含幅值，因此前者对估计精度的改善最大。而TVSEE不受节点电压幅值量测影响的原因是电压与电流关系较弱，节点电压量测的影响可以忽略不计。由此容易看出，最优配置方案会优先配置对估计精度改善较好的量测，在较好的量测全部配置后，才会加入其他量测。

为了验证模型的正确性，又代入多种不同运行状态进行模型求解，仍得到同样的最优配置，结果见表2。

表2 改造的13节点配电网量测配置结果(NM=1～5)

3.2 改进的IEEE 37节点配电网测试

改进的IEEE 37节点配电系统算例标准接线图如图5所示，表3列出三相网络的支路节点数和可配置实时量测总数。

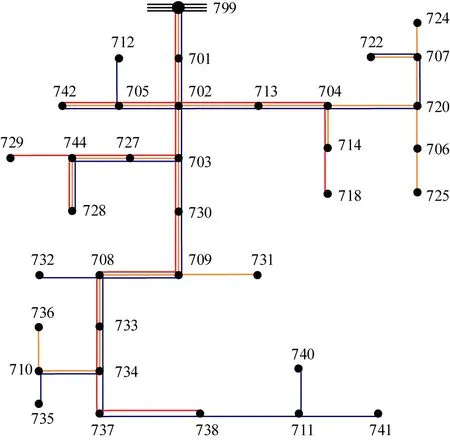
数字标号—节点代号。图5 改进的37节点配电系统标准算例接线图

表3 改进的37节点配电系统标准算例参数

综上可知，在提高估计精度方面，功率量测的改善效果要远好于节点电压或支路电流的幅值量测的，因此在本算例中，只考虑支路功率量测。设定NM为1～72，每次计算5 min，求解所有NM值时的最优配置方案。表4列出了NM为1～10时的最优配置结果，图6为TVSEE随NM变化的曲线。

由计算结果可知，对于基于支路电流的状态估计，其三相可信量测优化配置应遵循如下原则：

1)将支路功率量测作为优先配置的量测，其次是支路电流幅值量测；

2)在馈线首端附近位置优先的前提下，应均匀地配置于馈线上；

3)优先配置于三相健全的支路。

表4 改进的37节点配电网量测配置结果(NM=1～10)

图6 改进的37节点配电网状态估计误差总方差(TVSEE)随实时量测装置配置数NM的变化曲线

4 结语

状态估计可提供可靠、完整、一致的电网数据，保证配电网的可靠、灵活、高效运行。尽管随着配电网大量接入智能电表，高级量测体系逐渐形成，然而，可信的实时量测配置仍是配电三相实时状态感知所必需的。

针对传统量测方法普遍较为费时，且均为单相方法的特点，本文中提出了一种普遍适用于中压配电网三相可信量测优化配置方法，将三相TVSEE作为状态估计精度指标，建立了三相可信量测优化配置模型，通过Cholesky分解将目标函数采用决策变量显式表达出来，从而可调用成熟的优化软件实现快速求解。该方法兼顾模型的求解质量和速度，与启发式算法相比，能够在保证计算精度的同时大幅提高计算速度，对于工程应用具有指导意义。