一类切换非线性系统的自适应反步滑模控制
2020-05-21王素珍代明星孙国法靳奉祥
王素珍,代明星,孙国法,靳奉祥
(1. 青岛理工大学 信息与控制工程学院,山东 青岛 266520; 2. 山东建筑大学 测绘地理信息学院,山东 济南 250101)
在过去的几十年,非线性系统控制领域已有许多研究成果。Krstic等[1]于1995年提出反步法,目前已成为解决非线性系统控制问题的一种非常有效的方法[2-4],但是,传统的反步法需要已知的系统模型信息,并未考虑系统的未知不确定性,为其实际应用带来了很多限制。由于模糊逻辑系统(FLS)和神经网络能够非常好地逼近未知函数,因此被广泛应用于对系统的未知不确定项的逼近处理并基于此进行控制器的设计[5-7]。众多学者也基于FLS和反步法,针对不确定非线性系统提出了许多不同类型的自适应模糊反步控制方法[8-9]。
近年来,切换系统[10]作为一种特殊的混杂系统在实际应用中越来越广泛,针对它的研究也越来越多,关于该系统的控制方法的研究也取得了不少成果。针对非线性切换系统,自适应模糊反步控制也是一种典型的控制方法[11-13]。Li等[14]结合FLS并基于反步法的控制框架,针对一类纯反馈非线性切换系统设计了一类控制方法,取得了较好的控制效果。尽管这种方法可以实现对非线性切换系统的控制,但是在反步法设计过程中容易导致控制系统参数复杂性急剧增长,影响控制效果。此外,该方法假设系统各阶状态已知,在实际应用中具有较大的局限性,而且该方法并未考虑外界未知扰动所带来的影响,导致系统的鲁棒性不强,因而不能很好地应对外界扰动所带来的影响,无法取得更好的控制效果。
由于滑模变结构控制的结构特殊,具有很强的鲁棒性,因此能很好地应对外部扰动和参数摄动带来的影响。滑模控制对系统形式要求较高,需满足匹配条件,但大多数切换非线性系统并不满足匹配条件。此外滑模控制也有一个比较明显的问题,即容易产生抖振,从而影响控制效果。
本文中针对以上问题,对于一类不确定切换非线性系统,在反步法控制框架下,结合滑模控制,设计了一种新的自适应模糊反步滑模控制器。该方法首先利用FLS构造一种切换模糊状态观测器,从而实现对系统不可测状态的观测,便于后期控制器的设计,并通过FLS实现变比例控制,从而达到抑制抖振的效果。此外,利用高阶滑模微分器对系统未知扰动进行精确估计补偿,从而简化控制器的设计。对于反步法设计过程中导致被控系统参数复杂性急剧增加的问题,本文中通过引入二阶滑模非线性微分器直接对每一步中的虚拟控制信号进行求导,从而有效解决了传统反步法控制中的弊端。最后对这种控制方法进行仿真,通过仿真结果进一步验证该方法的有效性。
1 被控系统模型及准备
1.1 系统模型描述和假设
考虑一类严格反馈切换非线性系统,其形式如下:
(1)

本文中的研究目标是设计一种反步滑模控制方法,既可以达到控制效果,确保被控系统的稳定性和系统内所有信号的有界性,又使得被控系统的跟踪误差可以收敛在以原点为中心的一个小领域内。
为了便于控制器的设计,给出以下几点假设。
假设1存在一个已知的正数li,j,使得

假设2对于系统(1)的任何一个可能的参考信号xr,di, σ(t)(X,t)的n+1-i次微分都是有界的,即
di,σ(t)(X,t)∈Cn+1-i,
式中:ζ>0,是一个已知常数;Cn+1-i表示所有的微分函数集合。
1.2 模糊逻辑系统
模糊逻辑系统[5-6]一般包含4个部分,其中模糊逻辑系统的知识库是由一系列模糊if-then推理规则组成,

thenmisGl,l=1,2,…,n,

(2)

定义模糊基函数为
(3)

m(b)=θTφ(b)。
(4)
引理1[5]将f(x)定义在紧凑集合Ω上的连续函数,那么对于任意的常数ε>0,总存在如下的FLS:
(5)
2 模糊状态观测器
在本节中,针对被控系统内的不可测状态量xi(i=2,3,…,n)构造了一个切换模糊状态观测器,实现对这些不可测的状态量的观测估计,以便于后期控制器的设计。
针对切换系统(1)的第j个子系统,设计观测器
(6)
式中:
C=(1,0,…,0)T,Hi=(0,0,…,1,0,…,0,0)T。
定义观测器误差为
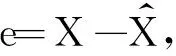
(7)
则
(8)
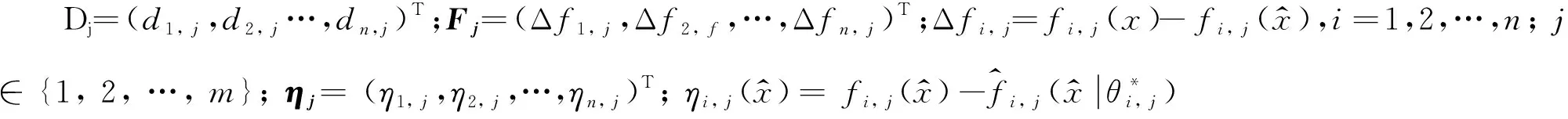
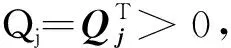
(9)
对于第j个子系统,假设di, j(t)=0,并选取李雅普诺夫函数V0=eTPje,那么
(10)
式中:

3 控制器设计及稳定性分析
3.1 高阶滑模微分器
由于高阶滑模微分器[15]具有在有限时间内收敛到被估计微分信号精确值的特点,因此可以对被控系统的扰动信号进行估计补偿,从而简化了控制器的设计,提高系统的控制性能。
对于系统(1)的第j个子系统,高阶滑模微分器可被定义为如下形式:
(11)

此外,本文中将引入二阶滑模微分器对反步法设计过程中的虚拟控制信号进行微分处理。二阶滑模微分器的形式为
(12)
二阶滑模微分器可以由图1直观地表示。

f(t)为微分器输入信号; z0, j为微分器输出信号; λ0, j和λ1, j为微分器可调参数;误差非线性函数图1 二阶滑模非线性微分器
本文中以符号xi,c, j(t)表示每一个滤波器的输出信号z0,i, j(t),虚拟控制信号αi, j则是作为滤波器的输入信号,并满足初始条件z0,i, j(0)=αi, j(0),z1,i, j(0)=0。
3.2 自适应反步法滑模控制器设计
本节中将在反步法控制框架下结合滑模控制方法,设计一种新的自适应控制方法。在进行控制器反步法设计过程之前,首先利用高阶滑模微分器(11)观测估计第j子系统内的扰动di, j(i=1,2,…,n),以便在控制器设计时对系统内的未知扰动进行补偿。

ek, j∈Cn+1-k。
(13)
基于式(13),接下来进行反步法控制器设计。反步法设计过程分为n步进行,首先定义切换系统第j个子系统的跟踪误差为
(14)
步骤1针对误差ζ1, j设计如下的虚拟控制律及自适应律
(15)
(16)

选取李雅普诺夫泛函
(17)
式中r1, j为正常数。对V1, j求导得
(18)
假定x2, j=α1, j,利用Young不等式,并将式(15)、(16)代入可以得到
(19)
步骤i针对误差ζi, j设计如下的虚拟控制律及自适应律:
(20)
(21)
选取李雅普诺夫泛函
(22)
式中ri, j为正常数。对Vi, j求导得
(23)

(24)
反步法迭代设计到此为止,最后一步是将滑模控制与反步法相结合,设计一种反步滑模控制器。
步骤n考虑切换系统第j个系统的第n个子系统的误差ζn, j。
定义一个滑模面
sj=cζn-1, j+ζn, j,
(25)
对式(25)求导,得

(26)
选取趋近律[17]
(27)
式中ρ和λ均为正实数。
基于滑模面(25)和趋近律(27),可设计如下的控制律
(28)
参数自适应律设计如下
(29)
本文中设计的控制律(28)会因符号函数项signs的不断切换而产生抖振现象,而符号函数的增益λ会影响抖振的强度。抑制抖振的方法有很多,FLS或神经网络等智能算法就是非常有效的方法。本文中基于系统(4)设计变增益的反步滑模控制方法,设计步骤如下:
1)定义FLS的输入为滑模面s,输出为增益λ。
2)分别定义FLS输入和输出的模糊集为{NB,NS,ZO,PS,PB},分别表示负大、负小、0、正小和正大。
3)设计模糊规则
4)求解FLS,获得输出
(30)

基于式(30),可以得到新的系统控制律
(31)
系统的稳定性证明如下。
证明:定义李雅普诺夫函数
(32)
对式(32)求导,并将式(31)代入可以得到
(33)

结合式(10)、(24)、(33),并将式(29)代入,利用Young不等式
(34)
(35)
进一步化简得到
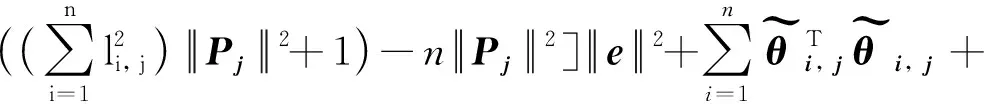
(36)
对式(36)进一步化简,最终得到
(37)
式中:
对式(37)两边同乘以eajt并在两端积分可以解得
(38)
由式(38)可以得到,跟踪误差ζ1会渐进收敛到以式(39)为圆心的一个小的邻域内,即
(39)
因此,只需要通过合理设计参数aj和bj,就可以保证系统稳定,并使得系统输出跟踪上参考信号。
4 仿真
本节中将对具体的算例进行仿真,对本文中所提出的控制方法的控制效果进行验证。考虑如下的一个二阶非线性切换系统。
子系统1:
(40)
式中
子系统2:
(41)
式中
选取参考信号为yr=3sin 2t+2cos 0.5t。
切换系统的切换信号σ如图2所示。当σ=1时,系统工作在子系统1的模式;当σ=2时,系统工作在子系统2的模式。

图2 切换系统的切换信号σ
系统的仿真结果如图3—6所示。系统输出x1跟踪参考信号yr的跟踪效果在图3中给出。由图可知,系统输出信号x1可以快速跟踪上参考信号yr,并且跟踪误差ζ1能够收敛在0值的小邻域内,验证了系统的跟踪性能。

(a)系统输出信号

(b)系统输出跟踪误差图3 参考信号跟踪效果及跟踪误差ζ1
高阶滑模微分器对系统未知扰动的观测效果如图4所示。通过合理选择高阶滑模微分器的阶数及参数,使其能够实现在有限时间内对系统未知扰动的观测逼近。
图5、6给出了观测器对系统状态的观测效果。由图可以看出,观测器能够在有限时间内实现对系统未知状态的跟踪观测,并且观测误差e可以收敛在一个很小的范围内。
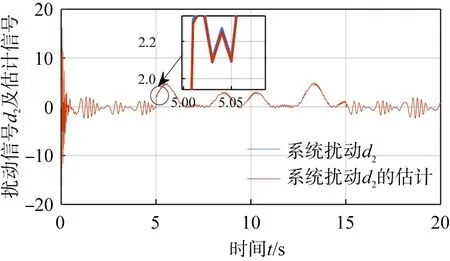
(b)系统扰动d2的观测效果图4 系统扰动观测效果

(a)系统状态x1及其观测信号

(b)观测误差图5 系统状态x1观测效果
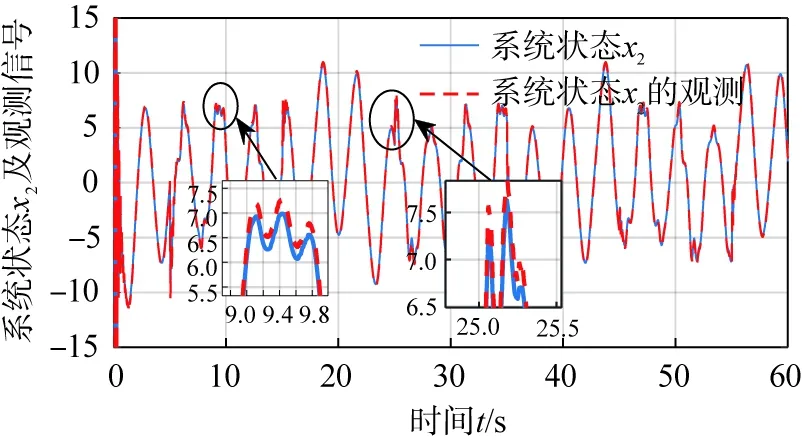
(a)系统状态x2及其观测信号

(b)观测误差图6 系统状态x2观测效果
5 结语
针对一类不确定严格反馈非线性切换系统的控制问题,基于高阶滑模微分器和模糊状态观测器提出了一种新的自适应反步滑模控制方法。利用模糊逻辑系统对未知非线性项实时在线逼近,并实现变比例控制。引入高阶滑模微分器对系统未知扰动精确估计补偿,增强鲁棒性,简化控制器的设计,并通过非线性微分器的使用避免了反步法设计过程中控制参数复杂性急剧增长的问题。仿真结果验证了本文中提出的方法具有较好的控制效果。
