An LCC-HVDC Adaptive Emergency Power Support Strategy Based on Unbalanced Power On-Line Estimation

Congshan Li, Jian Guo, Ping He, Yukun Tao, Cunxiang Yangand Youyi Wang

(1. School of Electrical and Information Engineering, Zhengzhou University of Light Industry, Zhengzhou 450002, China;2. School of Electrical & Electronic Engineering, Nanyang Technological University, Singapore 639798, Singapore)

Abstract: HVDC auxiliary power control can significantly improve the transient stability of AC/DC power grid. An HVDC adaptive emergency power support method based on unbalanced power on-line estimation is proposed in this paper. By establishing the extended state equation of the system, the on-line dynamic estimation of unbalanced power of the system was realized. On this basis, power support was realized based on the principle of the ladder increment. The optimal DC was selected by the power support factor, and the emergency power support controller was installed on the DC. This emergency power support method can realize dynamic optimal power support with minimized control cost. The three-infeed HVDC system was built on PSCAD. The simulation results show the effectiveness of the proposed method.

Keywords: emergency power support; unbalanced power; extended state observer; ladder-increasing principle; multi-infeed HVDC system

1 Introduction

With the development of large power grid interconnection, disturbance occurring in the interconnected power grid are extended to neighboring areas. If oscillation cannot be inhibited in time, it may cause serious power system fault. For AC/DC interconnected power grid, due to the rapid regulation characteristics and overload capacity of HVDC, exerting additional transient control on it can restrain grid oscillation and improve interconnected power grid stability. A large number of experts and scholars have conducted extensive research in this aspect[1-10].

DC emergency power support is an effective method to damp power oscillation in AC/DC power grid. Refs. [10-11] study the DC active power and reactive power modulation to increase the transient stability of AC/DC system. In terms of designing auxiliary damping controller, there are mainly two kinds of designing methods. One is model-based method, the other is model-free method[12]. For model-based methods, because the system order is high, the mathematical model of the system usually needs to be obtained through the identification method[13]. Recently, extensive research have been carried out, which propose power oscillation damping and maintain the frequency stability of the interconnection system applying sliding mode control[14], model predictive control[15-16], neuro-fuzzy feedback linearization[17], and Lyapunov theory[18]. Limiting factors of emergency DC power support are studied in Ref.[19]. As can be seen from the literature, present research on HVDC emergency power support mainly focuses on two aspects:

1) Research on limiting factors of power support.

Owing to the need to consume a large amount of reactive power during HVDC normal operation, the reactive power limitation needs to be considered when the DC active power is increased. In addition, the power limitation of the DC system itself is taken into account.

2) Research on emergency power support amount.

The emergency power support amount is an extremely important parameter for damping system oscillation. The appropriate amount can effectively suppress grid oscillation. If the amount is not suitable, it will not only fail to damp the system oscillation, but also deteriorate the system.

How to determine the amount of power support is an extremely important research topic. The key factor that determines the amount of power support is the system unbalanced power. According to current research work on emergency power support, we find that the determination of emergency power support needs complex calculation[20-21], which is time-consuming and difficult to achieve on-line dynamic support. With the application of wide area measurement system (WAMS) in power system, HVDC wide area additional control becomes possible. Based on this, the extended state observer (ESO) of unbalanced power is established to realize on-line estimation of system unbalanced power, and then to optimize the emergency power support by considering the constraint conditions. Finally, the principle of ladder-increasing is adopted to realize the goal of emergency power support. Through the simulation of multi-infeed HVDC system, the effectiveness of the method in this paper is verified.

2 Emergency Power Support Mechanism

In the study of transient stability of power system, the system is often equivalent to a two-machine instability mode. The system is divided into a critical groupSand a remaining groupA, so the problem of the power angle stability becomes the relative oscillation of the critical groupSto the remaining groupA. The transient equations of the critical groupSand the remaining groupAare as follows:

(1)

(2)

where

whereMS,δS,ωS,Pmi, andPeiare the equivalent inertial time constant, power angle, angular frequency, mechanical power of uniti, and electromagnetic power of the critical groupS, respectively;MA,δA,ωA,Pmj, andPejare the variables of the remaining groupAcorresponding to the above, respectively.

Combining Eq. (1) with Eq. (2), the transient state equation of the two-machine system can be equivalent to the single-machine system, and the rotor motion equation of the equivalent single-machine system is

(3)

In the case of generator fault or large power load sudden start in the critical groupS, the situation will result in an instantaneous shortfall in the power of the critical groupS. When the mechanical power in the critical groupSis less than the electromagnetic power, the rotor will slow down. If power support is equivalent to mechanical power, by adding the emergency power support measures, formula (3) becomes

(4)

where ΔPmis the amount of DC emergency power support. From Eq.(4), it can be seen that through the additional DC emergency power support measures, the rotor frequency difference can be reduced, thus achieving the goal of stabilizing the power angle. The appropriate ΔPmplays an active role in stabilizing the power angle, and inappropriate ΔPmmay worsen the system performance. Obviously, ΔPmplays a vital role in regulating the system unbalanced power. The unbalanced power changes dynamically due to the system’s own regulation and load response. Through on-line estimation of unbalanced power of the system, dynamic emergency power support is achieved.

3 Unbalanced Power Estimator

The diagnosis of power system faults or disturbances using ESO have been studied in Ref. [22]. A virtual fault is constructed by introducing additional parameters into the HVDC state equation, and the fault is estimated by an iterative solution. Ref.[23] uses ESO method to achieve the motor rotor flux observation. ESO is the central component of active disturbance rejection control (ADRC)[24]. In a broader sense, ESO is a practical disturbance observer[25], which can deal with uncertain problems such as unknown system parameters, unknown load disturbance, etc.

Based on the previous studies, this paper proposes the application of ESO to study unbalanced power estimation in AC/DC interconnected systems. By equalizing the unbalanced power into a disturbance state quantity, its size is estimated, and an emergency power support strategy is formulated.

3.1 Basic Principle of the Extended State Estimator

The general expression of the system mathematical model is

(5)

(6)

wherexn+1(t) is the expansion state of the system, which can be estimated in real time. For the system (6), its expansion state observer is established as follows:

(7)

wherez1,…,znare the state estimated values of the original system,zn+1is the expansion state of the system, i.e., the estimated value of the unknown function,β1,…,βn+1are parameters of the extended state observer, and fal(·) is a non-smooth function as follows:

where 0<α≤1 anddis related to sampling step.

Eq.(7) shows that the system state can be estimated from the input and output of the system as long as the observer parameters are properly chosen, and the extended state observer is shown in Fig.1.

Fig.1 Extended state observer

3.2 Construction of Unbalanced Power Estimator

The system angular frequency is defined as the equivalent angular velocity of its Center of Inertia (COI) as follows:

The relationship between generator frequency change rate and system power variation is as follows[26]:

(8)

In Eq.(8), take (f0/MJT)ΔPas the disturbance of the system, mark it asw(t), then it can be written as follows:

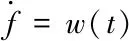
(9)

Eq. (9) represents a 0 input system, which can be written as a state equation as follows:

wherex1(t)=f,x2(t)=a(t)=(f0/MJT)ΔP.

According to the ESO principle, it can be written as an extended state observer as follows:

As for the actual power support, power support is not necessarily equal to the amount ofPm0due to the impact of power support constraints, soPm0is called pseudo control, but it should have a certain relationship withPm0.

4 Emergency Power Support Strategy Optimization

Without considering the dynamic characteristics of HVDC transmission lines, HVDC can be represented by a first-order inertia link. The dynamic process of HVDC power can be expressed as follows:

(10)

wherePdcREFis the set-point of HVDC power,Tdis the equivalent time constant of HVDC system,Pmis control variable of the system.Pmis not necessarily equal toPm0due to various influences such as self-regulation of grid, load characteristics, and power support constraints. MakeΔPm=k·ΔPm0, 0≤k≤1, substitute it into formula (10), then

wherekis control variable, which is related to the AC system frequency, equivalent inertia time constant. The value ofkis limited by many factors, which can be optimized by means of power support constraints.

4.1 Emergency Power Support Limiting Factors

Whether the DC system can reach the power which sets a value in accordance with the power boost command mainly depends on two limiting factors. One is the level of AC bus voltage, which is essentially due to the HVDC need to consume a large amount of reactive power in the promotion of active power, thus making reactive power insufficient and bus voltage drop, consequently resulting in the DC system’s inability to effectively enhance the power support. This limiting factor is directly related to the strength of AC system. The other limiting factor is the transmission capacity of the DC system itself. The HVDC system generally has 1.1 times long-term overload capability and 1.5 times short-time overload ability. In addition to overload operation, the DC transmission system also has the minimum power limit, which is determined by the minimum current limiting factor of the DC system. When the current is lower than the limit value, the DC current will be cut off.

For the limitation of AC system bus voltage, the voltage sensitivity factor (VSF) is defined to evaluate the limit of the AC system bus voltage level to the power increase in this paper. Specifically, it is defined as

(11)

If the value ofk·ΔPm0·ΔUis in the range of the voltage fluctuation, the value ofkis 1, the power boost is equal to the unbalanced power estimated by the observer. Otherwise, it is in accordance with the maximum admissible voltage fluctuation to calculate the value ofk. The limitation factor of HVDC transmission capacity itself can be realized by limiting amplitude.

4.2 Ladder-Increasing Principle for Power Support

Based on the kinetic theory and kinematics theory, once the equilibrium state of the object is broken, the external force should be adjusted in real time according to the movement state of the object so as to make the object smoothly transit into a new equilibrium state. Based on this, in case of emergency power support, power angle oscillation curve needs to be monitored in real time and made stable in a small scope in the whole transient transition period so as to ensure the smooth transition from transient state to stable state. SubstituteΔPm=k·ΔPm0into formula (4):

Fig.2 Power ladder-increasing principle

In Fig.2, the value ofNis affected by the intensity of the AC system. When the AC system is strong, the value ofNcan be appropriately reduced. Conversely, the value ofNis appropriately increased. According to previous studies, the value ofNranging between 5 and 8 is more appropriate.

4.3 Multi-Infeed Power Support Factor

Theoretically, during the fault period, each HVDC of the multi-infeed HVDC transmission system can achieve power balance for the AC/DC interconnected system by increasing the amount of power, but additional control effect on different HVDC has certain different influence. Multi-infeed power support factor is often used to select the optimal HVDC system for power support, which is defined as the product of AC/DC interaction factor (ADIF) or multi-infeed interaction factor (MIIF) and multi-infeed effective short circuit ratio (MESCR). ADIF was utilized to measure the degree of electrical coupling between AC and DC for AC/DC parallel transmission system. The greater the value is, the closer the connection is. MIIF is a measure of the degree of electrical coupling between DC system and DC system for multiple DC parallel transmission system. The greater the value is, the closer the connection is.

ADIF is defined as

where ΔUiis the voltage change of converter bus caused by switching a shunt reactive power branch on it when the DC system running at the rated power; ΔUjis substation bus voltage response variation for the AC system to be observed.FMIIF,jiis multi-infeed interaction factor and has the same definition asFADIF,ji, except that here ΔUjis expressed as the voltage variation in the DC converter station bus to be observed.

MESCR is defined as

whereSaciis the three-phase short-circuit capacity of the converteri;QCNiis the reactive power supplied by filter and shunt capacitor of AC bus in converter station;PdNiandPdNjare rated capacity of DC systemiandj.

Power support factor is defined as

λj,i=FADIF,ji×KMESCRi

The optimal control location for the multi-infeed HVDC system can be chosen by the maximum DC power support factor and achieve the best power support effect.

4.4 Optimal Emergency Power Support Strategy

In summary, the optimal emergency power support strategy can be obtained in this paper. First of all, the optimal control location is selected through the power support factor, then the unbalanced power can be estimated based on extended state observer, and power support optimization can be estimated based on power support constraints. Finally, power support can be realized based on the principle of ladder-increasing. The control structure is shown in Fig.3.

Fig.3 Power support control structure

Fig.3(a) is an extended state observer control structure, andfis the frequency of the equivalent inertial center of the AC system; Fig.3(b) is an auxiliary controller structure for the emergency power support.

5 Simulation Analyses

The three-HVDC transmission system with three machines was built on PSCAD, and the topology is shown in Fig.4. In this system, three HVDC lines all adopt standard CIGRE model, rectifier side fixed DC current control, and inverter side fixed turn-off angle control. The power of all the HVDC lines isPdc=1 000 MW,Vdc=500 kV. The generator model adopts detailed six-order model, which both contains excitation and speed regulation system, and all of them are not equipped with power system stabilizer. The generatorG1andG3rated capacity are 700 MVA,G2is 512 MVA, and inertia time constants of the three generators areH=6.5 s.

Firstly, the parameters of the second-order extended state observer are adjusted, and the tuning principle and the empirical parameter setting formula are used to adjust the parameters[25]:

wherehis the sampling step size. The effects of each parameter on system performance are as follows: whenanddincrease, the tracking of the state becomes slower, the steady state error becomes smaller; whenβ1increases, the tracking of the state becomes slower, the steady state error increases, and the overshoot decreases little; whenβ2increases, the tracking of the state becomes faster, the steady-state error increases, and the overshoot increases. Finally, the observer parameters are set forα/2=0.5,d=0.05,β1=20,β2=50. When the system is in steady state, the performance of the observer was tested, and the test results are shown in Fig.5.

Fig.4 Three-HVDC transmission system with three machines

Fig.5 Steady-state output

It can be seen from Fig.5, when the system is in steady-state operation, the rated frequency is 50 Hz. As shown in Fig.5, the unbalanced power of the system is 0. The estimated value of the observer is equal to the actual value of the system, and the actual value can be tracked quickly, which proves that the performance of the observer is good and the parameter setting is reasonable.

The system model established in this paper is three-infeed HVDC system, so there is no AC tie line. Therefore, only the multi-infeed interaction factors are calculated, and the factors is presented in Table 1.

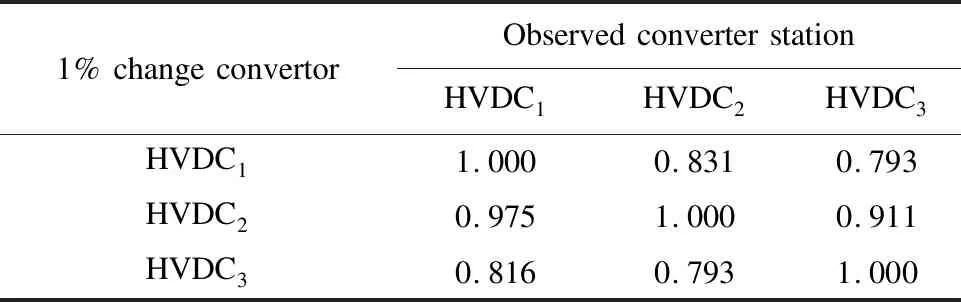
Table 1 Interaction factors matrix of DC/DC

The MESCR of HVDC1is 3.56, HVDC2is 3.78, and HVDC3is 4.67. When the active power imbalance is caused by internal disturbance of the AC system, only MESCR index can be used to select the optimal control location, i.e., HVDC3is the optimal additional control location for the internal disturbance.

It can be seen from Table 2 that when HVDC2fails, the control effect of HVDC3is better than that of HVDC1; when HVDC3fails, the control effect of HVDC2is better than that of HVDC1.

Firstly, the correctness of the control position selection was verified. Set two types of disturbance: type 1 is internal disturbance of AC system, which loses 552WM in BUS3 at 2 s and returns to normal operation at 4 s; type 2’s HVDC2fault occurs at 2 s and is cleared at 4 s, then HVDC2restarts. Comparison of different HVDC control effects are shown in Fig.6.

Table 2 DC power support factors

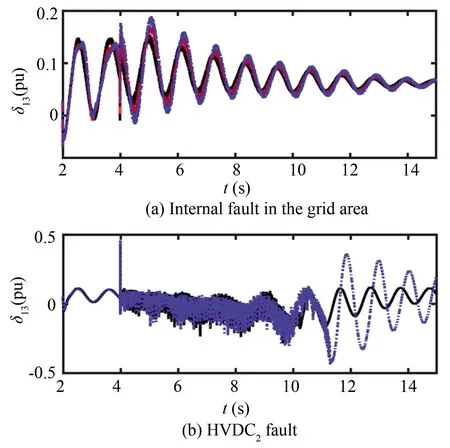
Fig.6 Control effects comparison

It can be seen from Fig.6(a) that in Case 1, the control effect of HVDC3is slightly better than HVDC2and the control effect of HVDC2is slightly better than HVDC1. For AC system faults, it is proved correct to select the optimal DC according to the MESCR indicator. In Case 2, the control effect of HVDC3is better than HVDC1. For DC system faults, it is proved correct to use the multi-feed power support factor to select the optimal DC. Through the comparison of simulation results, the correctness of the control position selection method is proved.

The following three cases were used to verify the effectiveness of adaptive emergency power support strategy proposed in this paper.

Case1:652MW is lost in BUS2 at 3 s due to fault.

The simulation results are shown in Figs.7-8.

Fig.7 (a) is the dynamic unbalanced power of the system estimated by the extended state observer. It can be seen from the diagram that the unbalanced power of the system is a dynamic quantity rather than a constant value. The black-dotted line is the unbalanced power of the system when the emergency power support controller is not put into use, and the solid red curve is the unbalanced power after the emergency power support controller is put into use. Comparison shows that the power balance in the system can be achieved quickly and stably after the emergency power controller is put into use.

Fig.7 Power curves in Case 1

Fig.8 Power angle curves in Case 1

Fig.7 (b) is the HVDC3power response curve. After the emergency power controller is put into use, the power balance can be realized quickly.

Fig.8 is power angle curve ofG1,G2, andG3. Comparison shows that it can effectively restrain the swing of generator power angle after the emergency power controller is put into use, and make system relatively smoothly transit to a steady state.

Case2:700WM load suddenly increases in BUS6 at 3 s.

The simulation results are shown in Figs.9-10.

Fig.9 Power curves in Case 2

Fig.10 Power angle curve in Case 2

Fig.9(a) is the dynamic unbalanced power of the system estimated by the extended state observer. Fig.9(b) is the HVDC3power response curve. Fig.10 is the power angle curve ofG1,G2andG3. As can be seen from Fig.10, with additional power control, the power angle offsets of the three generators are very small and recover quickly. The simulation results shows that the control effect is also very good for Case 2, as shown in Figs.9-10.

Case3: HVDC2is outage at 3 s and the fault is cleared at 5 s, then HVDC2restarts.

From Figs.11-12, it can be seen that the proposed method can also exert positive control effect for HVDC fault.

Through the simulation analysis and comparison of the three cases above, it can be found that the proposed method in this paper can dynamically and adaptively adjust the power transmission by itself according to the operating status of the system, and is effective in suppressing the power system oscillation. Therefore, the method is proved to be effective and robust.

Fig.11 Power curves in Case 3

Fig.12 Power angle curve in Case 3

6 Conclusions

In this paper, an adaptive emergency power support method based on the system unbalanced power on-line estimation was proposed, and the effectiveness of the proposed method was verified by simulation analysis. There are two main conclusions:

1) Power system unbalanced power changes dynamically during the transient process. Expanded state estimator can estimate unbalanced power online. Based on the estimated value, dynamic power support can be achieved.

2) For different types of power disturbance, there exists an optimal additional control location. For AC system internal faults, the maximum value of MESCR is used to select the optimal HVDC, and for HVDC faults, the maximum value of the multi-infeed power support factor is used to select the optimal HVDC.Selecting optimal power support realizes optimal power support with minimal control costs.

3) This method does not require complicated calculations and is easy to implement compared to existing methods.

The proposed method in this paper is a self-adaptable emergency power support method, which provides reference for the additional transient control of the actual AC/DC system.