低应变检测中振源及桩土相互作用的影响分析

丁玮，柴华友，刘思浩，陈灿，聂田，胡哲

(武汉工程大学 土木工程与建筑学院，武汉 430073)

低应变反射波法又称锤击-回波法，其基本原理为一维弹性杆应力波理论。通过在桩顶施加一敲击荷载，激发的弹性波沿桩身传播，当遇到桩身波阻抗变化截面时(如扩颈、缩颈、断桩等)，应力波会发生反射及透射现象。通过安装在桩顶位置处的加速度传感器可以接收到反射波质点速度响应，基于一维波动理论可以得到应力波沿桩身传播的平均速度、缺陷类型及位置，从而对桩身完整性进行判定。

实际上桩体是柱体，在应力波作用下，截面变形不均匀[1]，同时，应力波在传播过程中受桩土相互作用影响，这样，基于一维波动理论分析就有局限性，一些学者探讨了桩身应力波传播三维效应及桩周土对其传播的影响。Liao等[2]通过对比一维波动理论和三维数值模拟结果，研究了桩顶的三维效应，结果表明三维效应主要受频率影响，高频时表现更为强烈。陈凡等[3]分析了叠加在响应中的振荡，并将这种振荡解释为由于S波和R波在桩侧面的多次反射所致。Chow等[4]用轴对称有限元分析研究了源半径与桩半径比率对结果的影响，认为源和接收器之间的距离应大于0.5R，可以最大限度地减少第1个峰值后的反向(负向)过冲分量。Zheng等[5]通过理论分析认为，在0.6R处侧面反射波干扰影响最小。王雪峰等[6]基于应力波理论，系统地研究了桩顶不同部位质点速度响应的振荡程度以及应力波视速度等随锤桩比、波长桩径比、长径比的变化规律，给出了三维效应的动测规避方式。陈安国等[7]建立了以桩的连续杆件模型和土的线弹性模型为基础的低应变数值计算模型，并利用行波理论求解出波动方程。岳向红[8]基于理论、数值分析和工程实践，对基桩中应力波传播三维效应和衰减做出了探讨。陈辉等[9]对不同缺陷基桩的低应变反射波曲线进行数值模拟，得出反射波质点速度响应曲线，为实际基桩检测提供了理论参考。Chai等[10-12]分析了测点布置、振源特征波长与桩径比值对测试信号的影响。此外，桩土相互作用会影响波传播衰减及桩土系统动力响应[13]，研究桩土相互作用对应力波衰减的影响对基桩动测也非常重要。

由于桩是柱体，波在桩中传播不满足一维波动理论，因此，研究桩中波场对提高基桩结构完整性分析的精度非常必要。笔者将桩体波场分为距桩顶较近的近场及距桩顶较远的远场，基于波场成份及传播路径分析桩侧多次反射波影响较小的位置，基于柱体中纵向波传播特性，分析频率成份对远场波传播特性的影响，探讨了桩顶测试信号的一维近似条件。在桩土相互作用下，桩体应力波部分能量会向周围土体辐射，导致沿桩体向下能量不断衰减，笔者分析了桩土剪切波速等参数对桩土相互作用的影响。

1 桩中波场分析

1.1 桩顶近场

在均匀半空间表面上施加竖直向冲击源时，向下的P波和S波将会以半球形波前的形式传播，在介质体内遵循r-1的几何衰减定律，其中，r是距离源中心的径向距离。沿表面传播的直达P波和S波以r-2形式衰减；R波以圆柱形波阵面传播，并且遵循r-1/2的几何衰减定律。在P波、S波和R波中，R波的波速最慢，几何衰减最慢，所以，R波将主导远离源的表面场。S波和R波速度之间的回归关系可以近似表示为[14-15]

(1)

式中：cS、cR分别为S波速度和R波速度;v为泊松比。

桩顶中心振源作用下近场及远场波传播如图1所示，在到达桩的圆周侧面之前，桩中波与均匀无限体中波有相同的传播特性。在完整桩桩顶面中心区域用半正弦脉冲激振，数值模拟得到的不同时刻应力波竖直向质点速度幅值云图如图2所示，图中中间黑色矩形框表示脉冲作用区，白色虚线表示波前。可以看出，激发的球面P、S波与柱面R波相互叠加，无法识别出各类型波。

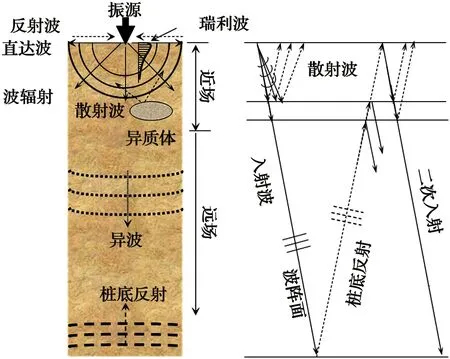
图1 桩中波的传播路径Fig.1 Ray paths of waves in piles

图2 桩侧面反射之前桩身质点纵向振动速度幅值云图Fig.2 Pile body particle longitudinal vibration velocity amplitude contour before pile side reflection

当波遇到桩侧面沿顶面传播的波在圆周侧来回反射，直到它们的能量消散。由于P波的垂直运动在桩顶的波场中相对较小，因此，垂直表面运动由S波和R波主导，多次反射波的基阶共振频率在式(2)所示范围[3]。

(2)

式中：R为桩半径，由于cR接近剪切波速cS，多次反射的共振频率约等于cS/2R。

1.2 桩顶远场

桩顶激振产生的下行波一部分在桩侧边界来回反射，反射波和向下传播波的相互叠加会在距桩顶较远处形成一种新的波，即导波。图3给出了P波和S波在边界反射，相互叠加在圆柱体形成导波的过程。取桩径为0.2 m、桩长为5 m的完整单桩，进行低应变数值模拟分析，图4为桩顶以下不同位置竖直向质点速度幅值云图。由质点速度沿截面分布可以看出，距桩顶较近波阵面是曲面(图中白色虚线)，桩轴线附近质点速度相对两侧较大，随着与桩顶距离增加，波阵面趋于平面，波阵面上质点速度分布也较均匀，表明波在远场近似一维杆波，在远场，下行波传播特性可以基于圆柱中纵向波传播分析。

图4 远场桩身质点纵向振动速度幅值云图Fig.4 Pile body particle longitudinal vibration velocity amplitude contour far from source

圆柱体中的导波有3种可能的传播模式：纵向、扭转和弯曲。纵向模式的位移纵向轴对称；扭转模式的位移主要在圆周方向上；弯曲模式是非轴对称的。当振源沿轴向施加于桩顶时，扭转和弯曲模式可以被忽略。圆柱体中，纵向导波呈现出多阶模态和频散特征。纵向模式的频散由Pochhammer频率方程表示[1]。

4ξ2αβJ1(αR)J0(βR)=0

(3)

式中：J0为第一类零阶贝塞尔函数；J1为第1类一阶贝塞尔函数。

ξ、α和β定义为

ξ=2π/λL

(4)

(5)

(6)

式中：ω和λL分别为纵向导波的圆频率和波长。模态截面位移分布与频率有关。在给定频率下，较高模态以较高的速度行进并具有较复杂的位移分布。

引入无量纲波数k=Rf/cP，其中，R是圆柱半径；f是频率；cP是纵波波速。对v=0.29，归一化基阶模态的频散和截面变形形状如图5所示[16]。

图5 圆柱中纵向波传播特性Fig.5 Longitudinal wave propagation characteristics in a cylinder

图中颜色较深的部分表示纵向位移。可以看出，当k足够小时(譬如k<0.1)，导波大致表现为平面波。也就是说，不同频率的波以几乎相同的速度行进，并且每个横截面变形近似均匀(参见图5中的阴影区域)。

2 一维波动近似条件

在实际低应变检测中，敲击脉冲可以近似用半正弦脉冲模拟，假设Td是半正弦脉冲的持续时间，脉冲的最大频率fmax≈1/Td。桩顶敲击激发的近场是三维的，波场含P、S、R波成份，可以用这些波的传播特性及在桩顶侧面反射来分析桩顶激发波响应。在远场，波传播特性可以用基阶模态纵向导波分析，由于图5频散仅与无量纲波数有关，为了建立敲击脉冲宽度Td与无量纲波数的联系，引入脉冲特征波长参数，脉冲的特征波长定义为

Wp=Td×c0

(7)

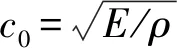
kmax=Rfmax/cRc0/(WpcP)

(8)

通过Ls-Dyna数值模拟方法分析敲击脉冲宽度及桩侧面反射波对桩顶不同位置质点速度响应及远场波传播的影响，并验证以上理论分析。缩颈桩模型如图6所示，桩直径(D=2R，R为半径)为0.5 m，桩长L为10 m，桩材料的杨氏模量E、密度ρ、泊松比v、分别取为40 GPa、2 500 kg/m3、0.25，侧面及桩底取为自由边界。a是桩顶圆形加载区域的半径，取a/R=1/8。在3个不同位置r/R=0.4、0.6、0.8处，无量纲脉冲特征波长Wp/R取4和8时，质点响应分别如图7(a)、(b)所示，r为测点与桩中心轴的径向距离。

图7 桩顶不同位置质点速度响应Fig.7 Responses at different radial positions for Wp/R=4 and Wp/R=8

图7中，第1个波峰是对应于冲击脉冲的响应(即直达S波和R波)，波峰后的振荡是来自桩圆周侧的多次反射，多次反射波共振频率满足式(2)。桩底反射后强烈的振荡是由基阶纵向波不同频率的波以不同的速度传播引起，即频散现象，圆柱中基阶纵向波频散曲线如图5所示。通过对比图7(a)、(b)可以发现，增大Wp/R的比例，可以抑制多次反射强度，特别当传感器放到离中心约0.6R的位置时，多次反射波在此位置范围出现相消干涉现象，多次反射波影响较小。

对于Wp/R=4的情况，kmax≈0.25，由脉冲产生的波分布在较宽的波数k范围内，频散现象较为明显，基阶模态在该范围内的频散导致尖端反射之后的强烈振荡，当比率增加到8时，kmax≈0.125，在此范围内，频散曲线较为平坦，相速度趋于一维杆中波速，截面变形后仍近似平面，在此情况下，圆柱中远场波近似为杆中波。图8为Wp/R=4、8情况下，位置r/R=0.6处桩顶质点速度响应与基于一维杆理论得到的响应比较。可以看出，当桩顶测点布置在r/R=0.6附近且敲击脉冲特征波长与桩径比值Wp/R较大时，远场反射信号可近似基于一维波动理论分析。

图8 Wp/R=4和8情况下，三维和一维结果比较Fig.8 Comparison of 3D and one-dimensional results for Wp/R=4 and Wp/R=8

3 桩土相互作用影响分析

上述分析表明，当敲击脉冲特征波长相对半径较大时，远场波传播可近似用一维应力波来分析，桩体向下传播应力波在桩土相互作用下，部分能量向周围土体散射，部分能量沿桩体向上传播，这导致向下传播的波不断衰减，衰减与桩几何参数及桩土剪切波速有关。通过数值模拟侧重研究桩土剪切波速对波传播影响，数值模拟桩长为5 m，桩身直径为0.2 m，桩周土外径为1 m，为模拟水平无限土体，避免人工土边界反射波影响，在土的外侧施加无反射边界。对低应变测试，桩土之间采用弹性接触。根据以上分析，为避免近场三维波动现象，对距桩轴线2R/3、桩顶1.5 m以下不同位置质点纵向振动速度幅值进行分析，为了比较桩土相互作用影响，以1.5 m位置的质点速度幅值为基础，对其他位置点质点速度幅值进行归一化处理。

3.1 桩身波速与土体波速

3.1.1 桩身波速 取土的剪切波速为50 m/s，密度为1 580 kg/m3，泊松比为0.44。桩身材料波速分别取为2 500、2 000、1 500 m/s，通过对数值模拟计算得到的响应分析，得到桩身质点纵向振动速度衰减曲线，如图9所示。

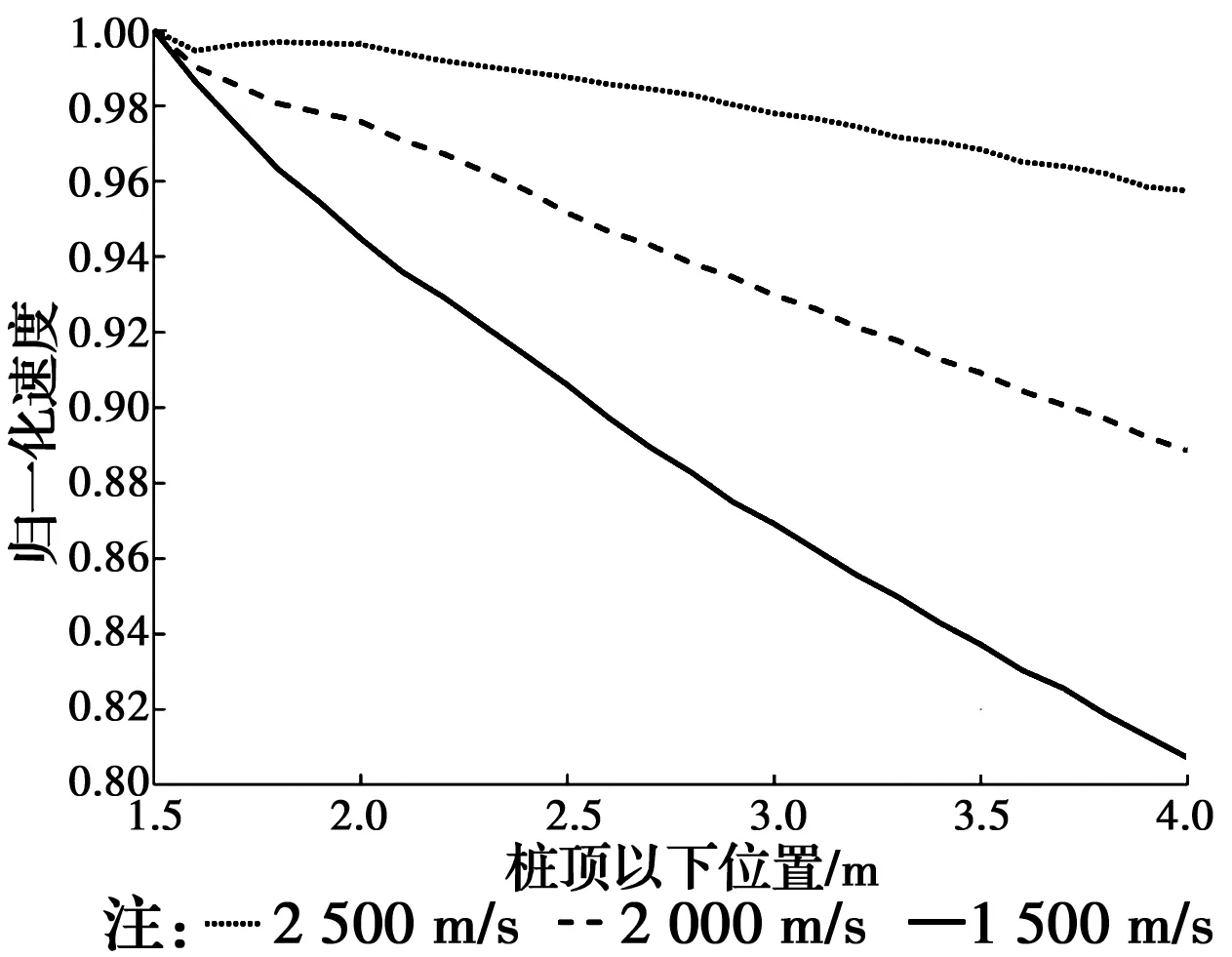
图9 桩体剪切波速对桩土相互作用影响Fig.9 Influence of shear wave velocity of pile on pile-soil interaction

由图9可以看出，桩身剪切波速不同，其桩身质点纵向振动速度衰减速率也随之发生变化，且随着桩体材料剪切波速的减小，衰减越快。即认为桩体材料剪切波速越小，应力波在桩身传播时的衰减速率越快。

3.1.2 土体波速 取土的密度为1 580 kg/m3，泊松比为0.44，桩体材料波速为3 000 m/s，改变桩周土体剪切波速，分别取50、60、100 m/s。衰减规律如图10所示。

图10 土体波速对桩土相互作用影响Fig.10 Influence of soil wave velocity on pile-soil interaction

桩周土体剪切波速不同，其桩身质点纵向振动速度衰减速率也不同，且随着土体剪切波速的增大，衰减越快。即认为桩周土体剪切波速越大，应力波在桩身传播时的衰减越快。

3.1.3 保持剪切波速比值不变 取土的密度为1 580 kg/m3，泊松比为0.44，桩身剪切波速分别取2 500、2 000、1 500 m/s，对应的桩周土体剪切波速分别取为100、80、60 m/s，从而保证3种情况下剪切波速比值为25，进行数值模拟分析，如图11。

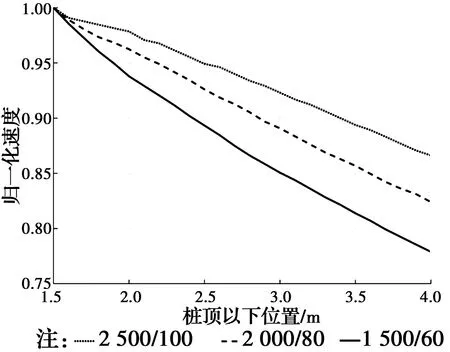
图11 桩土剪切波速比值不变情况下桩土相互作用的影响Fig.11 Pile-soil interaction under constant pile-soil shear wave velocity ratio

从图11中可以看出，虽然桩土剪切波速比值不变，但不同桩土剪切波速导致衰减不同，桩体剪切波速越低，则衰减越快，这表明桩土剪切波速比值并不是应力波衰减的决定性参数。

3.2 土体泊松比

取土的剪切波速为50 m/s，密度为1 580 kg/m3；桩身材料波速为3 000 m/s。改变桩周土体泊松比，分别为0.43、0.40、0.35，进行低应变数值模拟分析，得到曲线如图12所示。

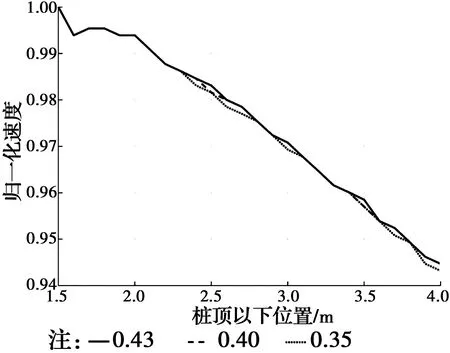
图12 土体泊松比对桩土相互作用影响Fig.12 Influence of soil Poisson’s ratio on pile-soil interaction

从图12可以看出，桩周土体泊松比不同，其桩身质点纵向振动速度衰减速率几乎一致。即认为桩周土体泊松比对应力波在桩中的传播衰减速率几乎无影响。

以上分析表明，桩体剪切波速与应力波的衰减速率负相关，桩周土体剪切波速与应力波的衰减速率正相关，土体泊松比对应力波衰减速率几乎无影响。

4 模型实验

缩径模型桩长3.3 m，几何参数见图13，缩径处完整系数为0.36。按设计尺寸将模型桩制作好，然后埋入预先挖好的坑中，经过一段时间固结后，进行低应变测试，测试信号见图14，桩体平均波速为3 654 m/s，为了考虑桩土相互作用的影响，取土的密度1 800 kg/m3，剪切波速150 m/s。基于一维波动理论，当完整系数取0.45时，测试与计算曲线达到最佳匹配，如图14所示。由于土体挤入模型桩缩径处导致完整系数比预设值大。这表明，可近似采用一维波动理论对远场反射波进行分析。

图13 缩径桩模型Fig.13 Neck pile model

图14 测试与计算曲线比较Fig.14 Comparison of measured and calculated curves

5 结论

1)在桩顶处施加脉冲作用，距源较近，桩顶附近波场呈三维波动效应，波场中含P、S、R成份，通过对这些波的波阵面、能量以及波在桩侧面反射分析可以研究近场波动响应；距振源较远的远场，可以用圆杆中纵向波传播特性进行分析，当敲击脉冲特征波长相对桩径较大时，远场纵向波相速度趋于杆波速，截面变形均匀，在此情况下，远场波近似于一维杆中波。

2)桩顶距振源约0.6R处，侧面反射波相消相干，侧面多次反射波影响程度最小，当测点布置在此位置，且敲击脉冲特征波长相对桩径较大，可以近似基于一维波动理论对远场反射波信号进行分析，但不适合对近场桩体反射波进行分析。

3)应力波在桩土相互作用下衰减不只与桩土剪切波速比值有关，更重要的是与桩体、土体剪切波速具体值有关，桩体剪切波速越低，土体剪切波速越高，应力波衰减越快。