不同含液量下颗粒间液桥力及形态的试验研究

蒲 诚，刘奉银，张 昭，程靖轩，赵 伟

（西安理工大学 岩土工程研究所，陕西 西安 710048）

1 研究背景

非饱和土的持水特性是其区别于其他类型土最主要的性质，正确认识非饱和土的持水特性是岩土工程性能评价的基础和关键，也是科学研究的热点问题。长期以来众多学者采用基质吸力、含水率、饱和度等参数来表征非饱和土的持水特性，取得了长足的进展。但是随着认识水平的提升，人们发现，不同初始条件下土样的持水特性反映的试验规律适用范围较窄、物理机制不清，加之不能观测到土样内部的变化情况，想要正确认识和从根本上揭示非饱和土持水特性的内在机制是远远不够的。作为一种典型的散体材料，当位于潮湿环境中时土体会从周围环境中吸收水分，在颗粒接触点处形成液桥，有学者认为非饱和土持水特性的变化过程从本质上可以归结为土颗粒间液桥力的演化，因而，从液桥的角度认识和解释持水特性日益为土力学界所关注。

对液桥的研究最早可以追溯到1960年代表面科学领域。随后，为了计算简单起见，Gillespie等［1］和Clark 等［2］将液桥的外表面假定为圆形；De Bisschop 等［3］、Pietsch［4］分别研究了两光滑球体以及粗糙球体颗粒间液桥的液桥力。Willett等［5］利用微分天平分别测量了等径与不等径人造蓝宝石颗粒间毛细力的变化规律；Damiano等［6］利用小挠度的悬臂装置，通过测量悬臂的变形来间接计算一对等径颗粒间液桥力的大小；Diana 等［7］、Wang Ji-Peng 等［8］在两颗粒拉伸试验的基础上进一步测量了三颗粒拉伸时液桥毛细力的变化。刘建林等［9］依据最小势能原理推导了轴对称液桥的形貌和液桥力；王学卫等［10］从数值模拟的角度研究了考虑重力影响下平板间液桥的断裂距离；庄大伟等［11］、朱朝飞等［12］分别从试验和理论分析的角度研究了狭长平板间液桥的形态。基于液桥理论，岩土工程学界的学者对非饱和土持水特性做出了积极的探索，Likos 等［13］研究了固-液接触角对非饱和土强度的影响；Yang 等［14］建立了基于固液接触角预测边界减湿土-水特征曲线的理论模型；Lu Ning 等［15］试验测量了两不等径颗粒间的液桥力，并从微观角度解释土-水特征曲线的变化规律。贺炜等［16］研究了颗粒间固液接触角对土-水特征曲线的影响；栾茂田等［17］从粒间液桥角度出发推导了非饱和土土水特征曲线公式；周凤玺等［18-19］理论推导了颗粒间毛细作用力并探讨其与土体液塑限的内在联系；张昭等［20-23］从理论角度推导了一对不等径颗粒间毛细力的计算方法，并将其延伸至黏土颗粒范围；余连英等［24］用微分天平手动测量了球形颗粒间液桥拉伸过程中液桥力的变化。

然而，国内对于液桥的研究主要集中在理论推导和数值模拟层面，本文利用一种全新的纳米拉伸装置，配合高清度CCD 数码相机，从试验角度测量和揭示三种粒径、六种含液量下一对等径球体颗粒间液桥力大小与形态的变化规律。

2 试验步骤

2.1 试验仪器采用美国Keysight公司研发的UTM T150纳米多功能试验机进行试验，在试验机的前侧以及左侧分别放置高精度显微照相机，确保上下颗粒处于同一轴线上并实时记录液桥形状的变化。试验机由刚性外壳、减振台、测量装置、数据采集系统四部分组成，刚性外壳可以最大程度减小液桥断裂时由于应力突然释放导致的波动；减振台可以消除周围操作人员的声音和脚步振动对试验结果产生的影响；测量装置主要由下端的机械驱动转换器以及上端可移动的刚性机械臂组成；数据采集系统分别连接在电脑和仪器的中央控制器上，用以操作仪器并实现数据的实时采集和分析处理，仪器构造示意图如图1所示，主要力学参数如表1所示。

图1 试验仪器示意图

表1 试验机的主要参数

2.2 试验材料选取3 组直径分别为2.5、4 和5 mm 的等径玻璃球；采用有机溶剂丙三醇模拟颗粒间的液桥，20 ℃时，丙三醇的性质如表2 所示。采用无水乙醇和去离子水作为清洗剂清洗玻璃珠表面［25］，以清除颗粒表面灰尘和消除颗粒表面静电力的影响。

表2 丙三醇与水的物理力学参数（20℃）

表3 液桥形态分类

2.3 液桥体积的确定选定0.05、0.1、0.2、0.5、1.0、1.5 μL六种液桥体积。Fournier等［26］、Rosset⁃ti等［27］根据饱和度的大小及液桥与颗粒间的联系方式，将液桥的形态分为如表3中所示的四类。

将颗粒间距D=0时颗粒间的孔隙视为孔隙体积VV，如图2中浅灰色所示；将液桥体积等同于孔隙中水的体积VW，如图2中深灰色所示；则有：

式中：V为液桥体积，μL；R为颗粒半径，mm。

当液桥为索带状、毛细管状以及泥浆状时，由于含液量较大饱和度较高，重力对液桥力及形态的影响一般不可忽略。而对于钟摆状液桥而言，Adams 等人通过研究重力与颗粒间液桥体积的映射关系，采用无量纲的液桥体积V*与BO数的乘积来定性反映重力对钟摆状液桥力及形态的影响，认为：当V*·BO＜0.01时，重力的影响可以忽略；当V*·BO＞0.015时，重力的影响不可忽略；当0.01＜V*·BO＜0.015时，处于过渡阶段［25］。

式中：d为特征长度，m，是液桥体积的函数；g为重力加速度，m/s2；Δρ为液体和外部气体的密度差值，kg/m3；σ为液体的表面张力，N/m。

BO数的概念最早用以表征重力对自由液体下落时液滴形状的影响，表示为BO=ΔρgD2σ，其中D为液滴的直径；随后，BO数被引入到液桥领域用来表征重力对球-板间液桥力与形态的影响，表示为BO=ΔρgR2σ，其中R为球的半径；而对于球-球间钟摆状液桥，Adams将其定义为式（2）的形式，其中d为特征长度，是一个无任何物理含义的值，Adams将其近似表示为其中V为液桥体积，D为液桥的直径。本文通过CCD 数码相机自带的图像处理软件ImageView 对不同条件下钟摆状液桥的直径进行量测，计算发现对于本试验而言特征长度值在0.3 mm 至1.5 mm 之间变动，为了计算方便统一取d=0.001 m。

对于本试验而言，Δρ=1260 kg/m3，g=9.81 m/s2，σ=0.067 N/m，颗粒半径R分别为2.5、4和5 mm。将其分别带入式（1）—（3）计算出不同粒径、不同液桥体积所对应的Bo 数、无量纲的液桥体积V*及饱和度Sr如表4 所示。由表4 可知：试验条件分别对应重力影响可以忽略、重力影响可忽略过渡状态以及重力影响不可忽略的情形，液桥形态分别为钟摆状、索带状、毛细管状及泥浆状。

2.4 试验步骤将清洗后的玻璃珠用硬基质胶固定在测量装置的刚性机械臂及NMAT 延长头上，采用微型移液枪在下部颗粒球冠处注入相应体积的液体，控制上部颗粒向下移动，待形成液桥之后反复拉伸多次使其形态趋于轴对称。试验时采用位移控制，确保上下两个颗粒接触距离为0，关闭试验机两侧及前侧的玻璃门使试验主体处于封闭状态，卸下减振台上的紧固螺栓，保持下部颗粒稳定，使上部颗粒以100 μm/s 的速度向上移动，设置荷载记录触发值为100 nN，同时利用CCD 工业电子显微镜记录试验过程中液桥形态的变化。

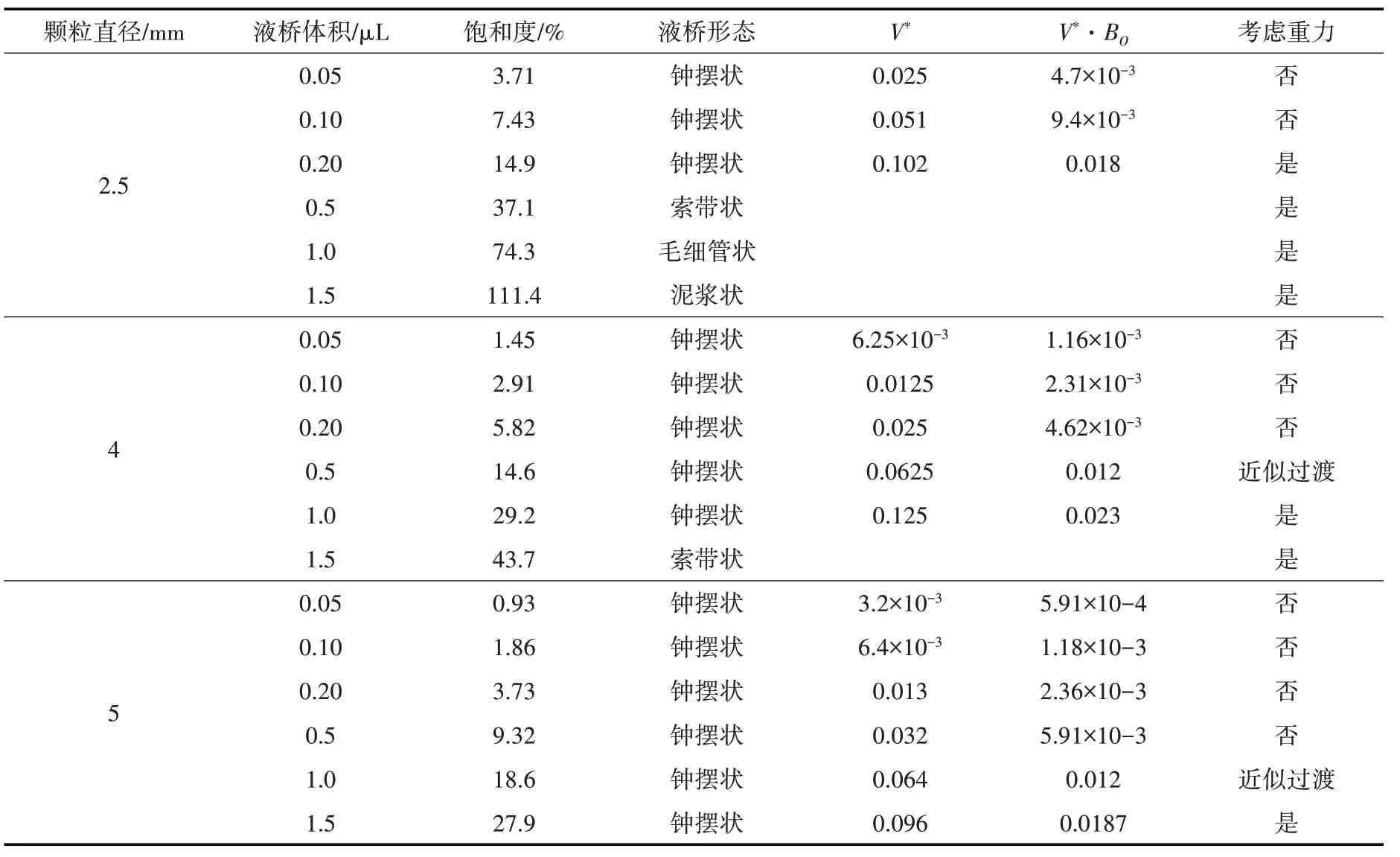
表4 不同液桥体积对应的Bo数及饱和度Sr

3 试验结果分析

3.1 液桥力-位移曲线分析张昭等［20］将粗粒样简化分散为球体颗粒，将水分形态视为液桥，认为液桥力Fliq是液桥中由基质吸力Fψ产生的毛细斥力以及由表面张力Fσ产生的毛细引力共同作用的结果，如式（4）；根据Y-L方程可将气液交界面处的基质吸力ψ表示为式（5），液桥颈部受力如图3所示。

图2 饱和度计算示意图

图3 液桥颈部受力示意图

图4 液桥几何参数示意图

式中几何参数如图4 所示，其中：r2为液桥颈部半径、r1为液桥外轮廓半径、R为颗粒半径。当Fσ＞Fψ时，液桥力为正，液桥形成；当Fσ＜Fψ时，液桥力为负，液桥断裂。

图5 为液桥力-位移曲线图，由图5 可知，曲线分为上升段、下降段以及突然跌落段三部分。在曲线的上升段，液桥力随着液桥拉伸距离的增大不断地增大，关于这一部分不同的研究者得出了不同的结论，Rossetti等［27］、Bozkurt等［28］认为最大液桥力出现在分离距离较小但不为零处，然而Olivier等［29］认为最大液桥力出现在分离距离为零处，虽然不同研究者对此持有不同的观点，但并未对此现象进行系统的分析，本文将在第四部分对其产生的原因提出猜想。在曲线的下降段，毛细斥力随着液桥拉伸距离的增加而增加而毛细引力随液桥拉伸距离的增加逐渐减小，但液桥内部仍以引力为主，当液桥的颈部变为最窄时毛细引力减到最小毛细斥力最大进入突然跌落段；当位于跌落段时，液桥不能再承受任何形式的拉伸，液桥突然断裂颗粒分离。曲线最后的残余部分为残留在下球表面液滴的重量。

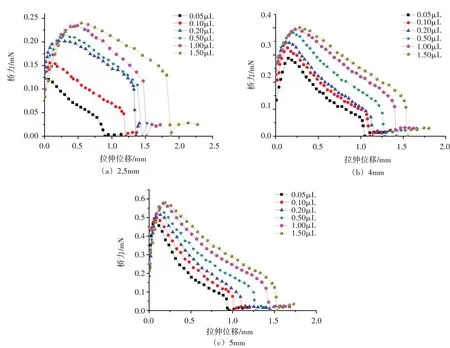
图5 液桥力-位移关系

定义曲线到达峰值点的位移为峰值位移。含液量对液桥力-曲线的影响主要以饱和度及Bo 数的形式反映在对上升段峰值位移及下降段曲线形态的影响上。在曲线的上升段，饱和度对曲线形态的影响较小，曲线峰值位移随饱和度的增加不断增加。在曲线下降段，当饱和度较小且重力影响可以忽略时，曲线下降趋势为“凹”状，如2.5 mm 颗粒0.05 μL 含液量以及5 mm 颗粒0.05～1.0 μL 含液量；当饱和度较大且重力影响不可忽略时，曲线下降趋势多成直线状或“凸”状，如2.5 mm 颗粒0.2～1.5 μL 含液量以及4 mm 颗粒1.5 μL 含液量。相对于含液量，无量纲的液桥体积更能反映液桥体积变化对曲线形态的影响，当液桥体积从0.05 μL增加至1.5 μL的过程中，2.5 mm 颗粒的无量纲液桥体积变化幅度更大，因而液桥力-位移曲线的下降段离散性及差异性也更明显。

图6 液桥形态变化图

3.2 液桥形态的变化利用CCD 相机全程录像，记录不同粒径及含液量下液桥形态的变化过程。由于篇幅的原因，本文仅以2.5 mm 粒径为对象分析不同含液量下液桥形态的变化规律。图6（a）至图6（f）分别反映了颗粒粒径为2.5 mm，液桥体积为0.05 μL、0.1 μL、0.2 μL、0.5 μL、1 μL、1.5 μL 等6种情况下液桥从形成到断裂的形态变化。用X 分别代表a 至f，图6（X-1）表示液桥的初始形态，图6（X-6）表示液桥最终断裂的形态，图6（X-2）至图6（X-5）分别反映了拉伸过程中不同时刻的液桥形态。

结合图6及表4可以发现液桥的形态是由重力以及饱和度共同影响的结果：当液桥体积为0.05 μL以及0.1μL时处于为钟摆状且重力影响可以忽略的情况，液桥的初始形态符合圆环假设，在颗粒接触点处形成如图6（a-1）、图6（b-1）所示的凹液桥，在拉伸过程中液桥始终保持钟摆状，当液桥最终断裂时液桥等体积的分布在上下颗粒的球冠处；当液桥体积为0.20 μL以及0.5 μL时分别处于毛细状液桥重力不可忽略以及索带状液桥的情况，液桥初始形态可近似为图6（c-1）、图6（d-1）所示的圆柱状，随着拉伸距离的增加液桥由圆柱状迅速变为图6（c-4）、图6（d-3）所示的符合圆弧假定的钟摆状，随着拉伸距离的增加重力对液桥形状的影响越来越明显当处于临近断裂时液桥形状为图6（c-5）、图6（d-5）所示的上部外曲率较小下半部外曲率较大的钟摆状，最终断裂时下球残留液体的体积稍大于上球残留液体的体积；当液桥体积为1 μL 以及1.5 μL 时分别处于毛细管状以及泥浆状的情况，此时重力的影响非常显著，液桥初始形态为外凸形并且发现了如图6（e-1）所示的非轴对称液桥形态，随着拉伸试验的进行液桥首先转化为圆柱状，后迅速变为图6（e-5）、图6（f-5）所示的上部外曲率较小下半部外曲率较大的轴对称钟摆状，最终断裂时下球残留的液体体积明显大于上球残留液体体积。

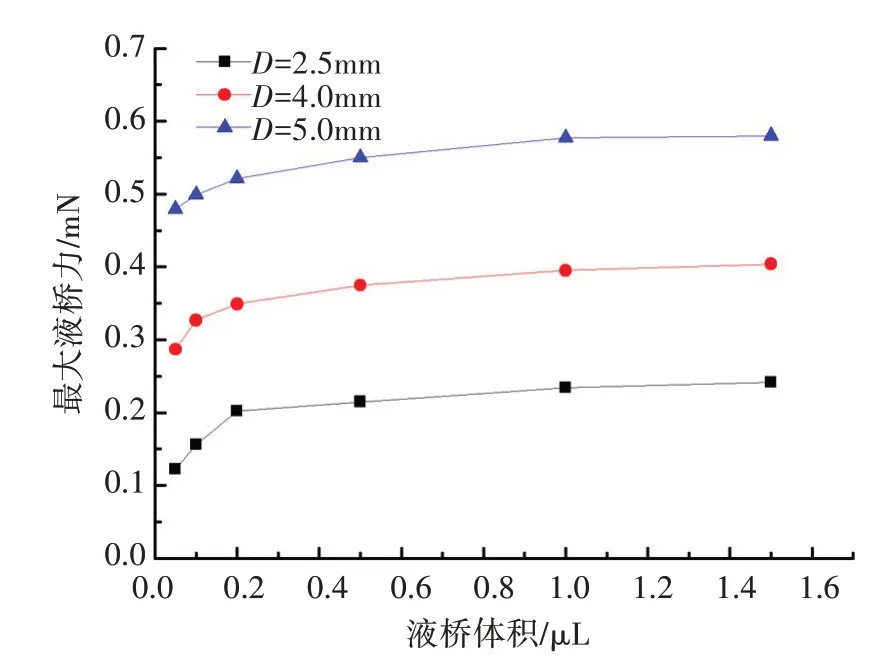
图7 最大液桥力-液桥体积关系

图8 断裂距离-液桥体积关系

3.3 最大液桥力及断裂距离分析将三种粒径，六种含液量下的最大液桥力和断裂距离分别绘制在图7 及图8 中。由图7 可以看出，颗粒间的液桥力经历了由快速增长到缓慢增长的变化过程：当液桥体积从0.05 μL增加到0.2 μL的过程中，随液桥体积增加液桥力增加速率较快，即使很小的液桥体积的改变也会导致液桥力的迅速增加；当液桥体积从0.2 μL 增加到1.5 μL 过程中液桥力随液体体积增加变化幅度较小。可以推论液桥力的增加必然存在一个阈值，即液桥力不会随着液体含量的增加而无限制的增加下去。相对于液桥体积，粒径对液桥力的影响更为显著，最大液桥力与粒径大小呈正比，含液量相同时粒径越大最大液桥力越大。

定义液桥突然断裂时对应的的拉伸距离为断裂距离。将断裂距离绘制在图8 中，由图可以看出，随着液桥体积的增加断裂距离也经历了由快速增长到缓慢增长的过程，且断裂距离随液桥体积的变化趋势与液桥力相同：当液桥体积从0.05 μL 增加到0.2 μL 的过程中，断裂距离随液桥体积增加的速率较快；而当液桥体积从0.2 μL 增加到1.5 μL 的过程中，断裂距离随液桥体积增加的速率放缓。粒径对断裂距离的影响更为显著，断裂距离与粒径大小呈反比，含液量相同时粒径越大断裂距离越小。

3.4 相关理论基于圆环理论，假定拉伸过程中液桥外轮廓半径以及固液接触角保持恒定，通过几何关系迭代并结合Y-L 方程，国内研究者［16，19-20］给出了钟摆状液桥液桥力的计算公式。Olivier 提出了一种认可度较高且较为简便的液桥力计算方法，如前文图5 所示，认为当R＞＞r1＞＞r2且液桥高度＜＜2r1cosθ时，液桥力可以表示为如式（6）所示的毛细力Fcap以及黏滞力Fvis的和：

图9 最大液桥力-液桥体积计算对比

图10 断裂距离-液桥体积计算对比

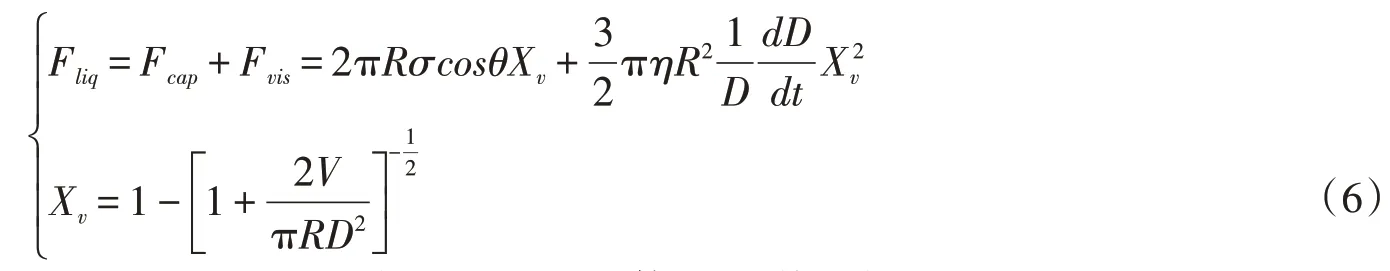
式中：σ为液体表面张力，N/m；θ为固-液接触角；η为液体的黏滞系数，Pa · s；D为分离距离，mm；dD/dt为分离速度。

Lian［31］给出了无量纲的断裂距离D*ruat与无量纲液桥体积V*及固液接触角θ之间的关系如下：

式中：D*rupt=Drupt R；θ取弧度值。

由于式（6）的限定条件，本文仅对含液量0.05 μL 不同粒径颗粒的液桥力-位移曲线进行模拟（如图9），将无量纲的断裂距离转化为实际断裂距离并与本文试验结果对比绘制在图10中。

可以看到，式（6）对于最大液桥力的预测较准且无量纲液桥体积越小预测的精度越高，但其无法预测液桥力-位移曲线的上升段以及突然跌落段，对于液桥力-位移曲线的缓慢下降段预测的精度不高，这也是目前所有基于圆环理论推导得出的液桥力计算公式的普遍困局。式（7）能较好地预测断裂距离随含液量增加而增加，随粒径增大而减小的趋势，但不能反映在重力影响较大情况下断裂距离增加速率随含液量增加逐渐放缓的趋势。

4 液桥力-位移曲线上升段机理猜想

对于液桥力-位移曲线的上升段，不同的研究者持有不同的观点，部分研究者认为最大液桥力出现在分离距离为零的位置，另一部分研究者认为最大液桥力出现在分离距离较小但不为零的位置。本文试图从试验方法的角度对曲线上升段产生的原因提出猜想。

以往的研究者大多采用微分天平法以或悬臂梁法测量液桥力。以悬臂梁法为例，试验时先将左侧球体颗粒固定在小刚度悬臂梁顶端，在右侧颗粒球冠处注入相应体积的液体将其固定在可移动的刚性悬臂端，保持左侧小刚度悬臂梁挠度为零，移动右侧刚性悬臂使颗粒间形成液桥，通过拉伸过程中小刚度悬臂梁挠度的变化计算液桥力。当采用悬臂梁法时，试验操作人员对初始点的选择对液桥力-位移曲线有很大的影响：如图11（a），当采用颗粒紧密接触临界位置为试验起始点时，液桥力-位移曲线则会观察到上升段；如图11（b），当采用小刚度梁不产生压变形的临界位置为试验起始点时，则液桥力-位移曲线没有上升段。随着试验技术的不断改进，高精度的刚性拉伸试验机开始广泛运用在液桥拉伸试验中。如图11（c），将试验机的核心部分简化为一个高灵敏度的弹簧和可移动的刚性悬臂，通过拉伸过程中弹簧的变形值来计算液桥力的变化，为了避免操作失误引起的刚性悬臂在下降过程中对下部弹簧造成损坏，在试验机设计时往往会预设部分弹簧伸长量以保护试验装置，而试验者通常采用位移控制上部颗粒向下移动以颗粒紧密接触临界位置为试验起始点，在试验开始时下部弹簧储存有一部分压变形。

综上所述，当试验以不发生压变形为初始点时，颗粒与液桥处于力平衡状态，但此时颗粒间的接触距离可能并不为零；当以颗粒紧密接触为初始点时，颗粒间的接触距离为零但此时液桥中液体对另一颗粒的顶端作用有压应力，随着液桥的不断拉伸，作用在颗粒顶端的压应力逐渐减小曲线呈现上升状态，即两种液桥力-位移曲线产生差异的根源原因可能在于其试验初始点的选择不同。

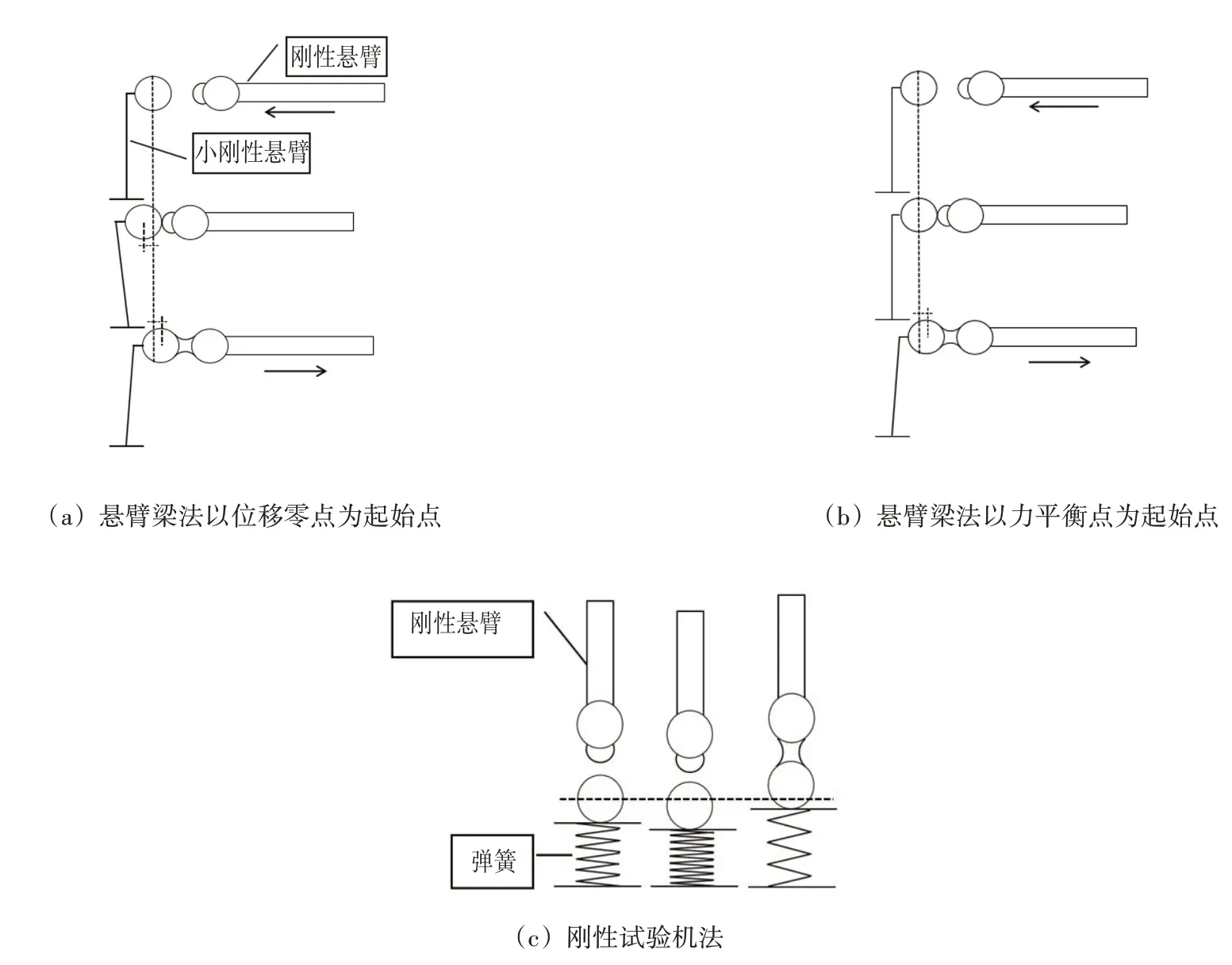
图11 不同试验方法示意图

5 结论与展望

使用纳米多功能试验机进行等径球体颗粒间的液桥拉伸试验，同时借助CCD 相机观测液桥形态的变化，从试验角度揭示了液桥力的变化规律，将试验结果与理论结果进行对比并初步探讨了液桥力-位移曲线上升段的产生原因，得到以下结论及展望。

液桥力-位移曲线可以分为上升段、平稳下降段以及突然跌落段三部分。当饱和度较小时且重力影响可以忽略时曲线下降段为“凹”状，当饱和度较大且重力影响不可忽略时曲线下降多成直线状或“凸”状，且相对于含液量，无量纲的液桥体积的差异更能反映液桥体积变化对曲线形态的影响。

液桥的初始形态受饱和度及重力的共同影响。钟摆状液桥主要出现在饱和度较低且重力影响可以忽略的情况下；当饱和度增加且重力影响不可忽略时，液桥的初始形态变为圆柱状及外凸状，并随着拉伸试验的进行转变为上部外曲率较小下部外曲率较大的钟摆状液桥。

随着液桥体积的增加，最大毛细力和断裂距离均经历了从快到慢增加的过程，低含液量下液桥力及断裂距离对液体体积的变化较为敏感。相对于液桥体积，粒径对液桥力及断裂距离的影响更为显著，最大液桥力与粒径大小呈正比，含液量相同时，粒径越大最大液桥力越大；断裂距离与粒径大小呈反比，含液量相同时，粒径越大断裂距离越小。

不同研究者观测到的两种类型液桥力-位移曲线，本文认为可能是由于试验初始点的不同导致的，关于这一猜想有待后续研究加以验证。