黄河流域水资源均衡调控理论与模型研究
2020-05-21彭少明畅建霞周翔南尚文绣
王 煜,彭少明,武 见,畅建霞,周翔南,尚文绣
(1. 黄河勘测规划设计研究院有限公司,河南 郑州 450003;2. 西安理工大学 西北旱区生态水利工程国家重点实验室培育基地,陕西 西安 710048)
1 研究背景
水资源调控是在特定的区域范围内,通过工程与非工程措施,对多种可利用水源在区域间和各用水部门间进行调配,以达到社会稳定、经济发展和生态保护的目的[1-2]。水资源调控一方面依据价值规律高效配置水资源,力求在不断加剧的区域与行业用水竞争中,充分发挥水在经济、社会、生态环境等方面的价值[3-4];另一方面需要协调低效益粮食生产、高附加值能源工业发展以及生态环境良性维持等基本用水,避免效益最大化导致用水失衡,实现水资源在区域、行业之间高效利用与公平分享[5-6]。
缺水流域水资源供需矛盾尖锐,区域与行业间用水竞争激烈,经济、社会、生态环境等多类用水协调十分困难,需要在用水效率和公平之间做出权衡,水资源调控难度极大[7-9]。国内外针对缺水流域水资源调控问题开展了诸多研究。早期的缺水流域水资源调控研究主要关注水资源产生的经济效益,通过供水成本、直接经济效益等单一目标指导水资源调配[10-12]。随着水资源调控理论与技术的发展,水资源调控目标由单一的经济效益发展到多目标,水资源的综合价值和不同行业间的用水公平开始被用于指导水资源调配[13-14]:一些研究通过权重、统一度量标准等方法将水资源的社会价值、经济价值和生态价值合并为单一目标考虑[15-17];另一些研究通过多目标优化分析水资源不同价值间的权衡关系,由决策者根据偏好选择最优的调控方案[18-19]。目前缺水流域水资源调控理论和方法研究已取得一定成果,对水资源价值、多目标配置等有一定探讨,但对区域公平、行业公平的考虑不足,公平指标极少出现在调控目标中,统筹公平与效率的缺水流域水资源调控理论和技术还有待研究。
黄河流域是我国水资源问题最为突出的区域之一,流域内水少沙多、水资源总量不足、供需矛盾尖锐、水生态环境问题长期存在[9,20]。近年来在变化环境的影响下,黄河流域水资源量持续减少、用水需求不断增长导致供需失衡进一步加剧[21-22],亟需创新水资源调控理论与方法以适应变化环境带来的新问题与新挑战。针对黄河流域严峻的缺水问题,本文从社会-经济-生态环境复合系统的角度出发,研究水资源利用效率核算方法,分析区域、部门之间用水的竞争性关系及用水公平的表征方式,提出统筹效率与公平的缺水流域水资源均衡调控理论与方法,建立黄河流域水资源均衡调控模型并进行实例研究。
2 缺水流域水资源均衡调控理论
2.1 水资源均衡调控定义水资源均衡调控是通过统筹兼顾流域内区域及行业间用水效率及用水公平性,实现水资源的可持续利用与生态环境系统良性维持。
用水公平性是指用水活动参与者平等享有满足自身发展所需水资源的权利,用水公平性问题是水量分配中最基本的问题,是水资源可持续利用的核心问题[23]。用水效率是指用水活动中的某种产出量与其投入的水资源量之比,反映了用水水平的高低,在经济活动中一般产出量常用经济价值衡量[24]。效率与公平是水资源调控中具有冲突的两个主要目标。效率优先的配水原则下,水资源被优先分配给单方水价值高的用户:经济价值高的工业用水与生活用水得到优先供给,而缺水多发生于经济价值低的农业灌溉用水;在缺乏适宜的生态价值评估方法时,河道内外生态用水也难以得到保障。公平优先的配水原则下,追求各用水户的缺水率相近或相同:缺水流域水资源的总供水量低于总需水量,遵循公平优先原则时,所有用水户发生程度相近的缺水,这种情况下由于不同用水户承受缺水的能力差异较大,因而缺水的影响存在较大的差别,如农业缺水对经济社会的影响相对较小,生活缺水却可能造成巨大的经济社会损失。
水资源均衡调控的内涵、内容、方向及手段。(1)调控内涵。按照自然规律和经济社会发展规律,统筹公平与效率两方面,实现水资源可再生性维持、经济可持续发展、社会公平合理、生态环境良性维持。(2)调控内容。空间上实现省际、河段之间的用水协调;行业间实现生活、生产、生态之间的用水有序;时间上实现年际与年内分配的用水合理。(3)调控方向。资源维的调控方向是水循环稳定健康或可再生性维持。经济维的调控方向是使水资源由低效率行业向高效率行业流转。社会维的调控方向是用水的公平性,保障弱势群体和公益性行业的基本用水,主要包括:生存和发展的平衡,即保证粮食安全和经济发展之间的平衡关系;区域间、国民经济行业间、城乡间的用水公平。生态环境维的调控方向是系统的持续性,确保重点生态环境系统的稳定和修复;在适宜和最小的生态环境需水量之间,寻求水循环的生态环境服务功能和经济社会服务功能达到共赢的平衡点。(4)调控手段。综合利用工程、资源、经济和管理等手段,统筹公平与效率等方面,通过水资源的科学合理调控,达到流域资源、经济、社会和生态环境的协同发展。
2.2 水资源均衡调控方法水资源均衡调控的目标是提高用水效率、维护用水公平,因此水资源均衡调控是一个多目标决策问题:

式中:FV为流域用水效率表征函数;FE为流域用水公平表征函数;x为待优化的配水量;gh(x)为水资源分配过程中需要遵守的第h个约束条件。
在水资源稀缺的情况下用水效率和公平协调存在冲突,均衡调控就是要对效率和公平进行权衡,而多目标优化的结果是得到FV和FE的非劣解集(Pareto 前沿),并不能给出最佳调控方案。
水资源是国家基本的公共自然资源,水资源配置本质上是自然资源配置,主要问题是如何兼顾公平与效率。福利经济学是研究社会资源配置在什么条件下达到最优状态和如何达到最优状态的一门学科,是经济学的主流分支[25],效率与公平既是福利经济学所追求的基本社会目标,也是它的基本政策目标。如何在公共资源配置中实现效率与公平的均衡,不同发展时期对于公平和效率的侧重应该如何抉择,是福利经济学所要解决的主要问题,不同的福利函数有不同的目标导向:古典功利主义的福利函数仅考虑了个体效用的简单加总和平均,忽视了社会个体之间的差别;精英者的福利函数因仅考虑效率、忽视公平,受到广泛的批评;罗尔斯的福利函数,强调最低收入者的福利,过分重视公平问题,因而可能导致社会缺乏激励机制、效率低下[26-27]。阿马蒂亚·森和福斯特的社会福利函数属于同一类型,他们都是社会平均收入和收入差别的二元函数,只是衡量收入差别的指标不一样,由于其同时考虑了效率与公平因素,成为了当今主流福利经济学的社会福利函数形式[25,28]。
实现公平与效率的均衡是新时期水资源配置追求的目标。本文在阿马蒂亚·森社会福利函数基础上,加入均衡参数α,构建效率与公平均衡调控的水资源配置社会福利函数,通过调节α来实现水资源配置的均衡,建立如下所示的水资源均衡调控函数:

式中:F为水资源调控效果的表征函数;α为均衡参数,取值范围0~1,α越大调控效果越偏重效率,α越小调控效果越偏重公平。
水资源均衡调控问题由式(1)转化为:

2.3 需水层次划分与调控原则根据水资源需求特点,可将需水分成3 个层次(图1):刚性需水,即满足生物生存、企业开工生产、河湖基本健康所需要的基本水量,一旦缺失将会造成难以挽回的损失;刚弹性需水,即提高生活品质、发展工业和塑造适宜生态环境所需的水量,缺水造成的损失是可恢复的;弹性需水,即维持生活中的奢侈消费、高耗水产业和人工营造高耗水景观所需的水量。
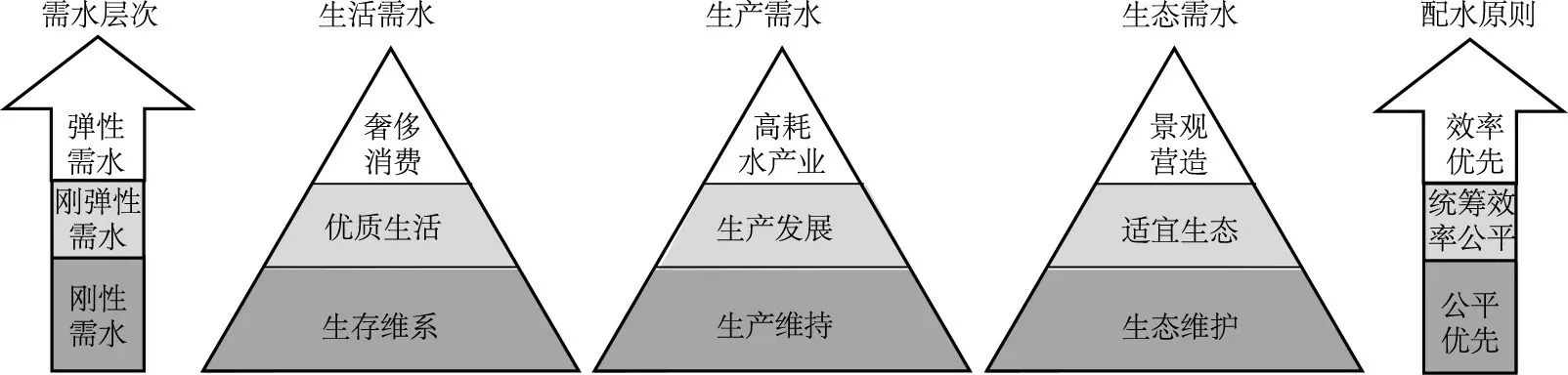
图1 水资源三层次需求
刚性需水在配水中位于第一优先级,配置时主要考虑公平原则,即式(3)中α=0;刚弹性需水在配水中位于第二优先级,配置时需均衡效率与公平协调,0<α<1;弹性需水在水资源调控中最后考虑,按照效率优先的原则配水,即α=1。在水资源调控中刚性需水一般能够得到满足,缺水流域难以支撑弹性需水部门的发展,因此缺水流域水资源调控中最重要的就是统筹效率与公平对刚弹性需水进行均衡调控。
3 用水效率与公平核算方法
3.1 用水效率核算方法用水效率反映了用水过程中产出量和水资源投入量之间的比值关系[24],当产出量采用价值衡量时,单方水的价值量便可以充分表征用水效率。水资源在人类社会、经济生产和自然环境中流通,产生社会、经济和生态环境价值。流域用水效率表征指标FV计算公式如下:

式中:K为流域内的分区总数;FV1,k、FV2,k和FV3,k分别为第k个分区的水资源经济价值、水资源社会价值和水资源生态环境价值。
水资源在不同领域产生价值的度量方法存在差异,水资源经济价值的计算方法相对简单明了,但水资源社会价值和生态环境价值的计算方法繁多且评估结果差异较大,不同价值的统一评估方法是水资源综合价值评估的难点[27]。能值是由美国生态学家Odum创立的度量标准,指一种流动或储存的能量所包含另一种类别能量的数量[28]。太阳能是社会-经济-生态环境复合系统最重要的能量来源,因此以太阳能为基准,能值分析方法能够将水资源在社会-经济-生态环境复合系统中产生的能源、原料、娱乐等多种价值转换成太阳能能值统一度量[29-30]。能值单位为太阳能焦耳(solar emjoules,即sej)。本文采用能值法计算水资源综合价值。
水资源经济价值计算公式如下:

式中:i=1、2、3、4 分别代表农业、工业、建筑业、第三产业;j=1、2、3 分别代表地表水、地下水、其他水源;WEC,i,j,k为第k个分区第i种行业第j种水源经济用水量,m3;τEC,i,j为第j种水源在第i种行业中的能值转化率,sej/m3;EECI,i,k为第k个分区第i种行业的投入总能值,sej;EECO,i,k为第k个分区第i种行业的产出总能值,sej。
水资源社会价值计算公式如下:

式中:WSO,j,k为第k个分区第j种水源生活用水量,m3;τSO,j为生活用水中第j种水源的能值转化率,sej/m3;ESOI,k为第k个分区的生活投入总能值,sej;ESOO,k为第k个分区的生活产出总能值,sej。
水资源生态环境价值计算公式如下:
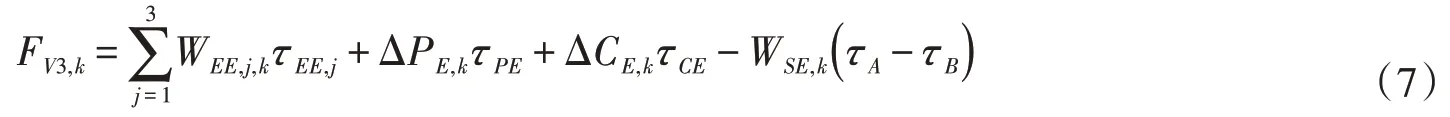
式中:WEE,j,k为第k个分区第j种水源河道外生态环境用水量,m3;τEE,j为河道外生态环境用水中第j种水源的能值转化率,sej/m3;ΔPE,k为第k个分区河道水体势能变化量,J;τPE为河道水体势能的能值转化率,sej/J;ΔCE,k为第k个分区河道水体化学能变化量,J;τCE为河道水体化学能的能值转化率,sej/J;WSE,k为污水排放量,m3;τA为污染前水体的能值转化率,sej/m3;τB为污染后水体的能值转化率,sej/m3。
3.2 用水公平核算方法本文根据配水量与3 层需水的满足程度关系(图1)构建满意度曲线(图2),提出用水满意度函数表达式:
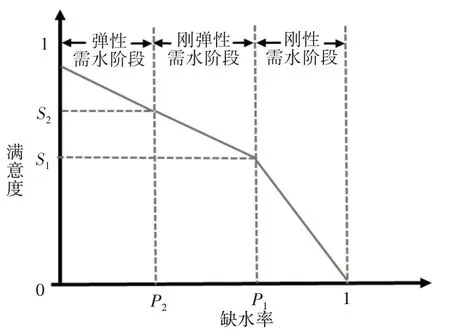
图2 满意度函数曲线

式中:P为缺水率;S(P)为用水满意度;P1为供水量等于刚性需水量时的缺水率;P2为供水量等于刚性需水量与刚弹性需水之和时的缺水率;S1和S2分别对应P1、P2缺水率下的满意度,本次采用经验法确定S1=0.5,S2=0.75,见图2。
将流域每一个分区内不同用水部门满意度的均值定义为主体满意度,代表一个区域主体对于供水情况的整体满意程度,反映了区域用水公平性,计算公式如下:

式中:Ak为第k个分区的主体满意度;n为流域内用水行业数量;Pi,k为第k个分区第i种行业的缺水率。
将流域不同分区内同一行业的满意度均值定义为部门满意度,代表一类用水部门对于供水情况的整体满意程度,反映了部门用水协调性,计算公式如下:

式中:Di为第i种行业的部门满意度;K为流域内分区数量。
基尼系数反映了收入分配不平等的程度,取值范围0 ~1,取值越大代表分配越不均。基尼系数在社会经济领域得到了广泛的认可和应用,因此本文借用基尼系数的概念和计算方法构建了用水基尼系数。用水基尼系数反映了水资源在不同地区及不同用水部门间分配的不公平性,取值范围0~1,取值越大表示水资源在地区或部门间的分配越不公平。基于用水基尼系数构建区域用水公平性指标FEA和部门用水协调性指标FED:

式中:GA是主体满意度Ak的用水基尼系数;GD是部门满意度Di的用水基尼系数。用水公平性指标FEA反映了不同分区的主体满意度Ak的差异,FEA越大代表各个分区的主体满意度越接近,即水资源在不同地区间的分配越公平;部门用水协调性指标FED反映了不同行业的部门满意度Di的差异,FED越大代表各个部门间的用水满意度越接近,即水资源在不同用水部门间的分配越协调。
将Ak从小到大重新排列生成新的序列A'k,然后计算A'k的累积频率ρA,m:

式中:1≤m≤K;令ρA,0=0。基尼系数一般通过洛伦兹曲线计算得到,图3中对角线代表最公平的分配曲线,面积C为实际的主体满意度累积频率曲线与横轴间的面积,面积B为对角线以下面积与面积C的差值。基尼系数为面积B与对角线以下面积的比值,即得GA计算公式为:
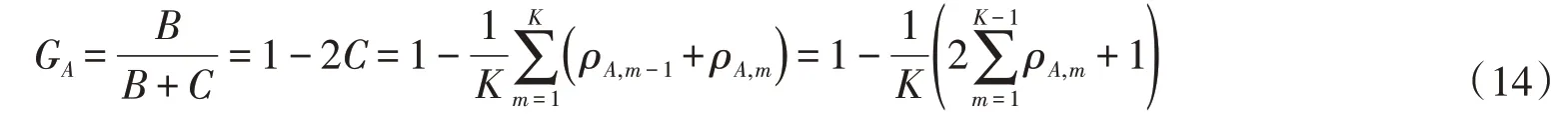
同理,可以得到部门满意度Di的用水基尼系数GD。流域水资源调控需要兼顾区域间的公平性和行业间的协调性,因此本文构建了流域用水公平表征指标FE,用来综合反映水资源在不同地区间及不同用水部门间分配的公平性:

4 黄河流域水资源均衡调控模型
4.1 模型结构黄河流域属于缺水流域,需水主要由刚性需水、刚弹性需水和弹性需水组成。黄河流域多年平均水资源量可以满足流域内刚性需水,需要在完全满足刚性用水需求的基础上,将剩余水量按照用水效率与公平协调兼顾原则进行合理分配。
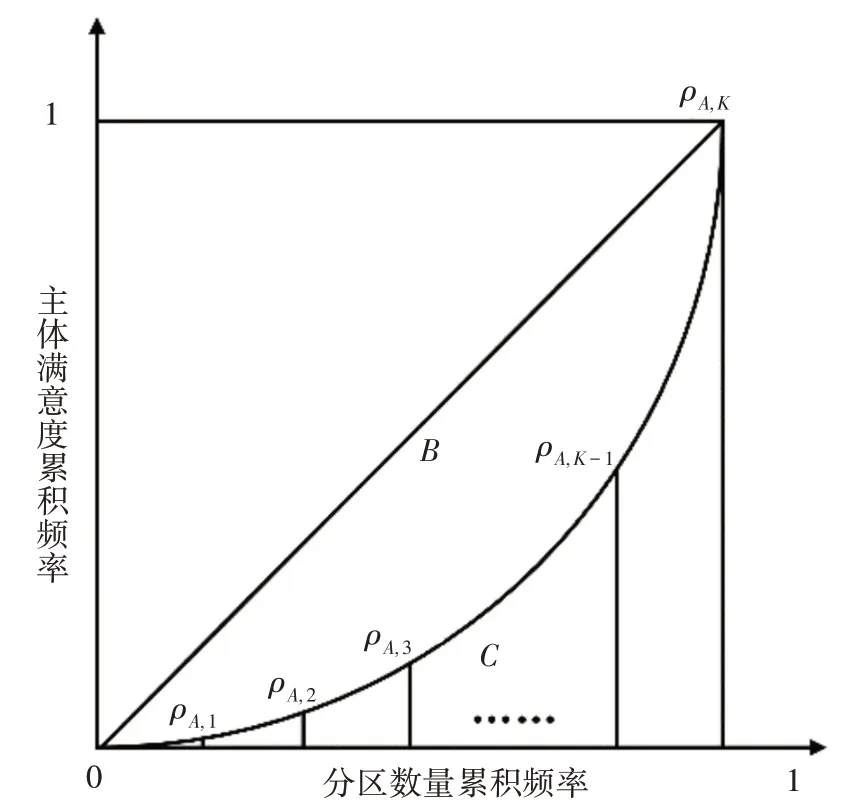
图3 洛伦兹曲线
黄河流域水资源均衡调控模型概化如图4 所示。将黄河流域按照省/自治区划分成9 个区域,分别是青海、四川、甘肃、宁夏、内蒙古、陕西、山西、河南、山东。模型包含55 个用水节点:将用水部门划分成6 个行业,分别是城镇生活、农村生活、工业、农业、城镇生态、农村生态,共计54 个河道外用水节点;将利津断面生态需水量作为全河生态需水量,设置1 个河道内生态用水节点。除河道内生态用水节点外,其它用水节点取水后仅消耗部分水量,余水将退回河道。
4.2 模型主要计算原理
(1)目标函数。模型的目标函数为:
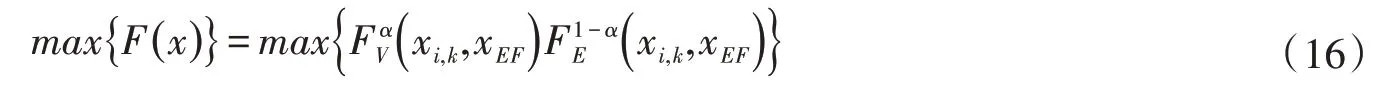
式中:xi,k为第k个分区第i个行业的供水量,i=1~6,k=1~9;xEF为河道内生态供水量。
(2)主要约束条件。①供需关系约束。供水量不应低于刚性需水,不应高于刚性需水、刚弹性需水和弹性需水之和:

式中:DRI,i,k、DRE,i,k、DEL,i,k分别为第k个分区第i个行业的刚性需水量、刚弹性需水量、弹性需水量;DEFRI、DEFRE、DEFEL分别为黄河河道内生态的刚性需水量、刚弹性需水量、弹性需水量。

图4 黄河流域水资源均衡调控模型概化
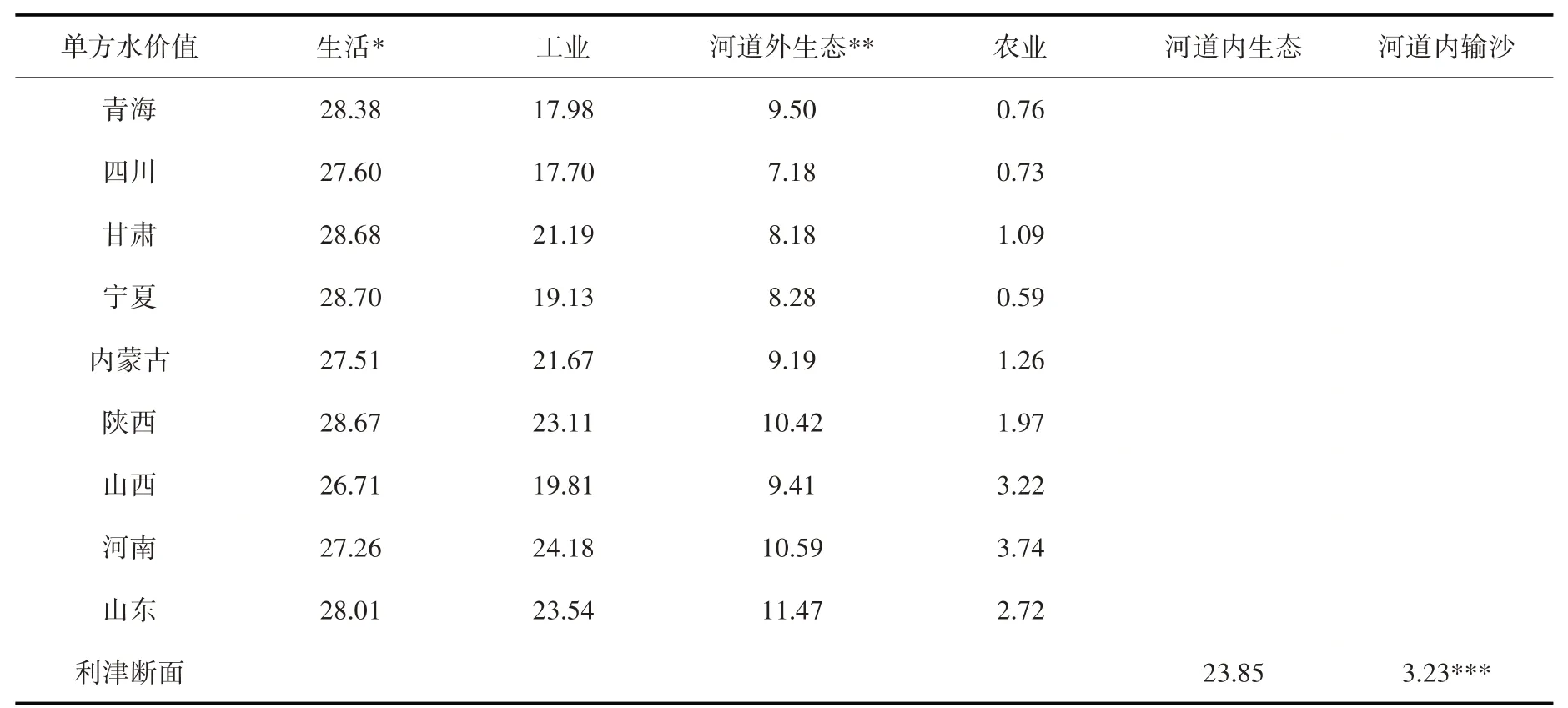
表1 黄河流域省区及关键断面单方水价值 (单位:m3/元)
②河段水量平衡约束。

式中:QIS,k为第k个分区所在河段的入流量;QLS,k为第k个分区的地表水产水量;QLG,k为第k个分区的地下水可开采量;βi,k为第k个分区第i个行业的耗水系数。
③分区入流断面水量约束。

式中:DEF,k、DST,k和DWP,k分别为第k个分区入流断面的河道内生态需水量、输沙需水量和水质净化需水量;θEF,k、θST,k和θWP,k分别为DEF,k、DST,k和DWP,k的折减系数,取值范围均为0~1,水量充足时取值为1,刚性需水无法完全满足时进行折减。
(3)求解方法。将各分区各行业的供水量及河道内关键断面的水量做为求解变量,采用带线性约束条件及精英策略的改进遗传算法进行迭代求解[31]。
5 实例研究
5.1 方案设置通过方案对比验证本文提出的水资源均衡调控模型的有效性及稳定性,进一步分析均衡参数与流域水资源配置的响应关系。设置方案如下:
(1)基准方案。以《黄河流域水资源综合规划》(以下简称《规划》)中2030年无西线工程配置方案为基准方案。该方案采用的年均天然径流量为515 亿m3(1956—2000年系列);在现有黄河流域供水工程的基础上,加入规划的干流骨干工程及调水工程(不含南水北调西线工程);考虑南水北调东线工程供水1.26亿m3,引乾济石调水0.47亿m3、引红济石调水0.90亿m3;流域内河道外需水量547.5亿m3;利津断面河道内汛期需水量170亿m3,非汛期需水量50亿m3。
(2)均衡方案。按照价值(本次效率用水资源综合价值代替)、公平主导程度设置15 个均衡方案,式(2)中α取值分别为0、0.01、0.05、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、0.95、0.99、1。均衡方案边界条件与基准方案一致。采用式(4)—(7)分别得到黄河流域内各分区的生活(城镇、农村)、工业、农业、河道外生态(城镇、农村)6 类用水的单方水价值及利津断面的生态、输沙单方水价值,见表1。根据表2 原则对黄河流域内河道外需水及关键断面河道内需水进行“刚性-刚弹性-弹性”层次划分,其中河道外刚性需水328.8 亿m3,占比60.1%;刚弹性需水182.5 亿m3,占比33.3%;弹性需水36.2 亿m3,占比6.6%。利津断面非汛期刚性需水采用关键期(4—6月)300 m3/s,非关键期(1—3月和11—12月)50 m3/s。利津断面汛期刚性需水采用1980—2016年实测汛期径流量的平均值112.2 亿m3;刚弹性、弹性需水根据《规划》中利津断面不同的淤积比确定。
5.2 结果分析随着福利函数中均衡参数α从0(公平优先)逐渐增加到1(价值优先),黄河流域内整体用水价值呈现逐渐增加的趋势,而用水公平性随着效率的提升而递减,见图5。
(1)流域内各省区供水量变化。如图6 所示,基准方案流域内河道外供水量为442.3 亿m3;均衡方案下流域内河道外供水量变化区间为416.9~457.8亿m3,当α取值0.5或0.6时,河道外总供水量与基准方案接近。随着α取值逐渐增大,用水价值较高省区的供水量及利津断面水量逐渐增加(图7),其余省区供水逐渐减少。
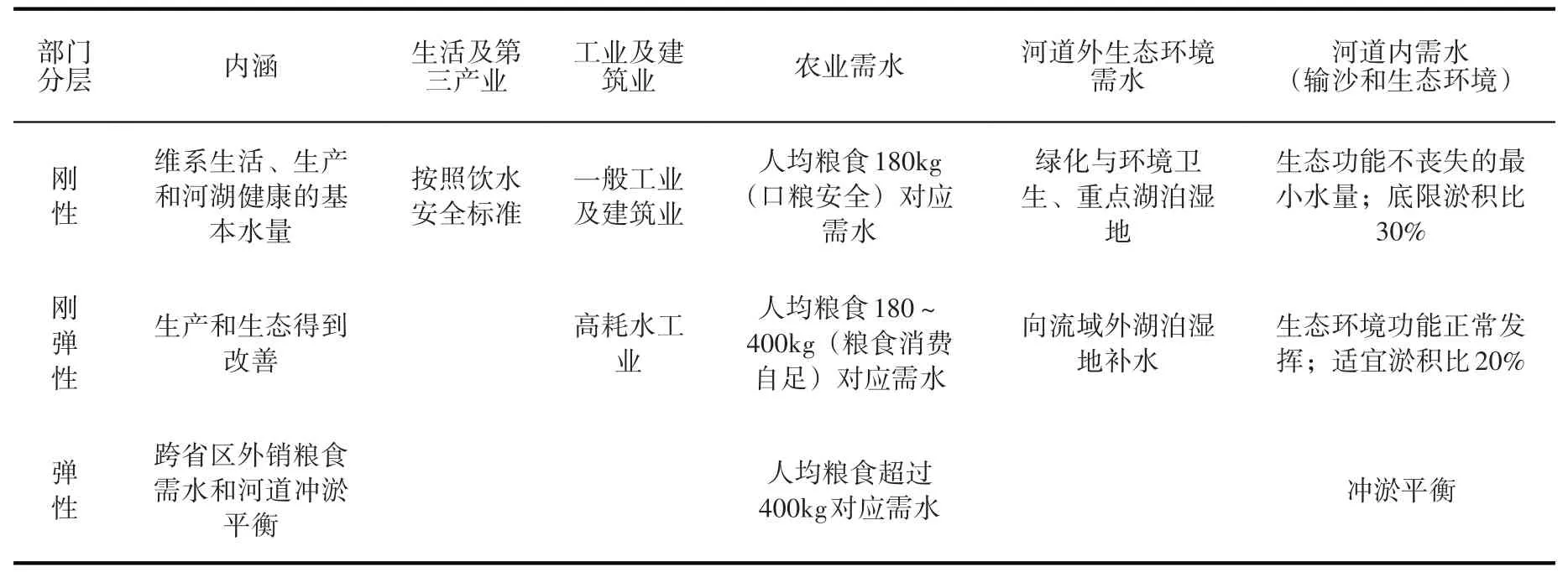
表2 黄河流域需水分层的基本原则
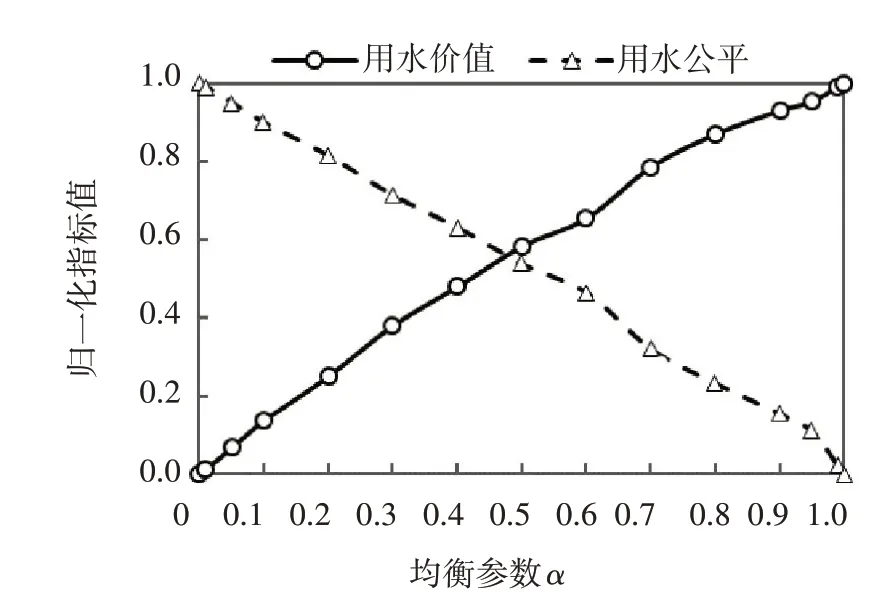
图5 不同均衡参数下黄河流域用水效率及公平的变化
(2)流域内地表耗水量与利津断面水量变化。基准方案与均衡方案流域内河道外省区耗水量与利津断面水量之和基本一致,均约426 亿m3。当α不超过0.3 时利津断面水量为179 亿m3;随着α的增加,均衡方案配置结果更加偏重于用水效率,利津断面水量不断增加;当α取值0.4 或0.5时,均衡方案与基准方案流域内河道外省区耗水量及利津断面水量基本一致;随着α的继续增大,利津断面水量进一步增加,当α=1 时,利津断面水量211.5 亿m3,河道外省区耗水量仅214.8亿m3(图8)。
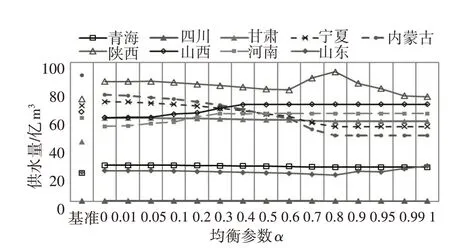
图6 基准方案与均衡方案供水量对比
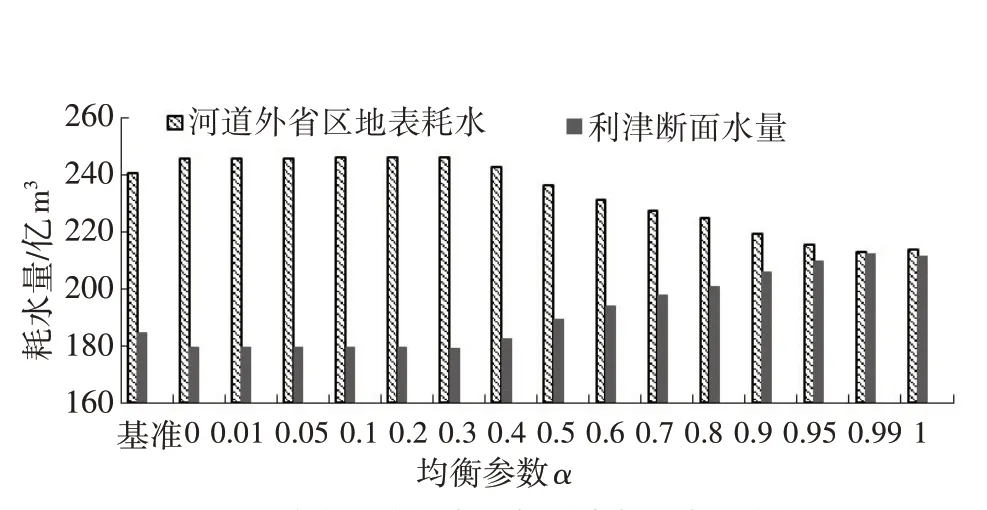
图7 流域内地表耗水量与利津断面水量变化
(3)价值量变化。由于均衡方案中的刚性需水得到完全满足,此处不对刚性供水的价值进行分析,供水价值为刚弹性供水价值和弹性供水价值之和。如图8 所示,当α取值不高于0.3时,河道内供水价值基本保持不变,这与该阶段利津断面水量基本保持不变有关;河道外供水价值呈现出递增的规律,模型在保持河道外耗水量一定时,将水资源分配给单方水价值更高的省区。当α取值大于0.3 时,河道内分配水量逐渐增多,价值随之递增;河道外省区按照单方水价值由低到高的顺序,逐渐减少弹性及刚弹性供水,从而导致整体河道外供水价值逐渐降低。总体来看,随着α取值从0 增加至1,由公平引导逐渐向效率引导过度,总供水价值从242.3 亿元增加至330.7 亿元;基准方案供水价值为256.1 亿元,与α=0.1 时均衡方案供水价值(254.5 亿元)接近。
(4)公平性变化(缺水率)。将弹性缺水率RSE定义为:

式中:ST为总供水量;DRI为刚性需水量;DRE为刚弹性需水量;DEL为弹性需水量。
如图9 所示,基准方案由于充分考虑河道内外用水协调,河道内总缺水率与河道外总缺水率接近,分别为16%和19%;但河道内外弹性缺水率差别较大,河道内弹性缺水率45%,河道外弹性缺水率61%。对于均衡方案,当α取值不超过0.3 时,配水原则以公平为主,河道内外总缺水率接近(河道内总缺水率16.6%、河道外总缺水率18.6%),河道内外弹性缺水率一致(52%);随后随着α的增大,配水逐渐向用水效率高的用户倾斜,导致河道内外缺水率差别不断扩大,河道内外弹性缺水率差别尤为明显;当α=1 时,河道内外总缺水率相差19.8%,河道内外弹性缺水率相差64.4%。
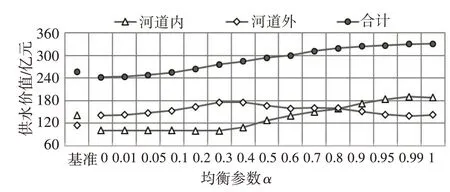
图8 基准方案与均衡方案弹性供水价值对比
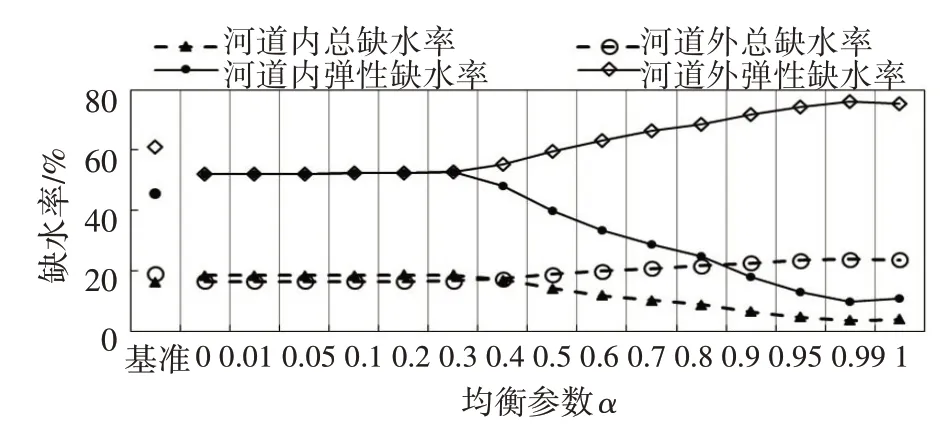
图9 基准方案与均衡方案弹性缺水率和总缺水率对比
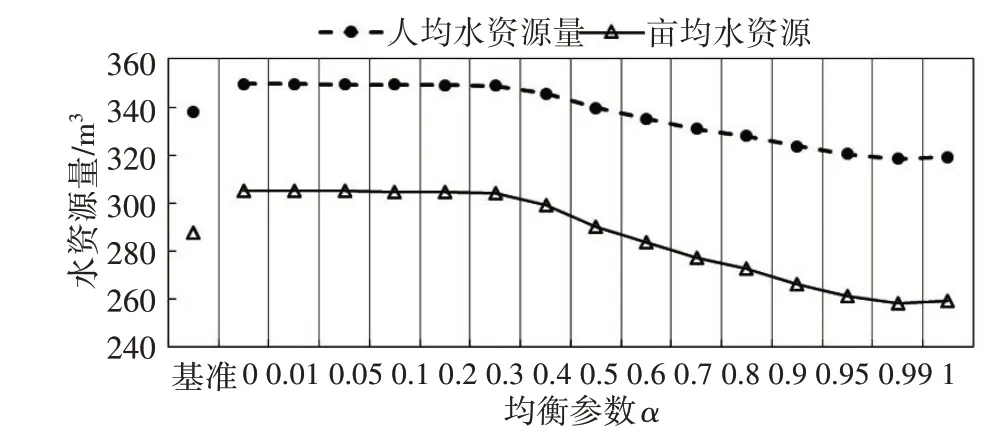
图10 基准方案与均衡方案人均水资源量对比
(5)人均供水量及亩均供水量变化。如图10所示,由于河道内输沙用水价值高于大部分省区的农业用水价值,随着α的增大河道内用水量逐渐增加,导致均衡方案中河道外人均、亩均水资源量不断下降;当α不超过0.3 时,人均、亩均水资源量基本稳定于349 m3/人、304 m3/亩;当α=0.5 时,均衡方案的人均、亩均水资源量接近基准方案(338 m3/人、287 m3/亩);当α=1 时,均衡方案的人均、亩均水资源量降低至319 m3/人、259 m3/亩。
(6)政策启示。面对尖锐的水资源供需矛盾,缺水流域水资源管理需要借助分析工具在用水效率和公平间做出权衡,均衡各种目标、策略,实现资源、经济、社会、生态、环境的协同发展,提升流域水资源对经济社会发展的支撑能力,提高河流生态服务功能。
6 结论
针对缺水流域水资源调控中难以协调效率与公平的问题,本文得出如下结论:
(1)定义了水资源均衡调控,提出了统筹用水效率与公平的水资源均衡调控函数,实现了不同水资源调控原则的融合;根据水资源需求特点对需水进行层次划分并明确了不同需水层次的水资源调控方法。
(2)基于能值理论提出了涵盖社会—经济—生态综合价值的流域用水效率表征指标;构造了分层需水的满意度曲线,基于基尼系数提出了区域用水公平性指标和部门用水协调性指标,兼顾区域公平和部门协调建立了流域用水公平表征指标。
(3)以黄河流域为例,综合考虑河道外社会经济和生态用水及河道内生态用水,建立了黄河流域水资源均衡调控模型。
(4)分析了黄河流域河道内外、省区之间用水效率及公平的变化规律,结果显示随着配水原则从公平优先向效率优先的转变,由于河道内生态用水价值较高,利津断面用水量从179 亿m3增加至211.5 亿m3,而河道内外弹性缺水率的差值从0 增加至64.4%,黄河流域算例通过调整均衡参数有效反映了水资源调控中效率与公平的转变过程,为黄河“87”分水方案优化提供技术支撑,也可为其它流域或区域的水资源均衡调控提供技术方法。
