基于鲁棒规划方法的农业水资源多目标优化配置模型
2020-05-21缑天宇张田媛
谭 倩,缑天宇,张田媛,李 然,张 珊
(1. 中国农业大学 水利与土木工程学院,北京 100083;2. 四川大学 水力学与山区河流开发保护国家重点实验室,四川 成都 610065)
关键字:多目标规划;权重不确定性;鲁棒性;农业水资源管理;种植结构
1 研究背景
水资源与农业生产和粮食安全息息相关,是维系社会可持续发展和生态系统稳定的重要因素。随着人口的不断增长,人们对粮食的需求不断提高。2050年全球人口预计将增长到95亿,届时粮食需增产60%、农业用水量需增加19%,才能满足基本粮食需要[1]。中国是个农业大国,农业是最主要的用水部门。在水资源严重紧缺的背景下,不协调的农业种植结构和较低的灌溉水利用率,将进一步加剧农业生产的困境[2]。尤其在我国西北干旱半干旱区域,在气候变化和人为活动的双重影响下,农业水资源匮乏和生态环境退化问题尤为突出[3]。合理配置农业水资源、提高农业水资源利用效率,对保障区域粮食安全和维护农业生态系统具有重要作用。
农业水资源优化配置,是协调区域作物生产和生态环境保护的需要[3]。调整作物种植面积、优化作物结构,是实现灌溉水资源优化配置和高效利用的有效途径之一[3-5]。农业水资源管理需要权衡多方利益,涉及经济、社会和生态环境等多方面。多目标线性规划方法,能够有效处理多个目标之间的权衡问题,在水资源的优化配置研究中广泛应用。Li 等[6]综合了机会约束规划、半无限规划和整数规划等方法,对甘肃石羊河流域地表水和地下水的联合利用进行了优化配置,得到了在不同水文年条件下的农业灌溉水资源优化配置方案。Kennedy 等[7]利用多目标规划模型,通过调整土地利用类型,在景观尺度上对经济和环境目标进行优化,使巴西农业可以同时满足农业生产、生物多样性和生态系统服务的要求。Ren 等提出了一种多目标模糊规划方法,构建了以社会、经济和生态效益为目标的多目标模型,在模糊参数的不同可能性水平下,对灌溉用水和土地利用进行了优化,得到了最优的农业灌溉方案[8]。Tan 等将分式规划与鲁棒优化相结合,建立了以单方水效益最大为目标值的水资源优化模型,同时处理了参数中存在的复杂不确定性信息,提高了农业水资源的利用效率[9]。
然而,农业水资源多目标优化问题的研究中仍存有难题。其一,在多目标求解时,往往需要借助决策者对不同目标的偏好信息,将多目标转化为单目标问题求解。这一信息由于受到决策者的主观偏好等因素的影响,不可避免地存在着不确定性。而现有的农业水资源多目标规划研究,往往忽略了或无法有效处理这样的不确定性信息。以最常见的线性加权方法为例,该方法将目标权重简化为确定值进行求解。若各目标权重值稍有变化,基于确定性权重求解得到的结果很可能变为次优解或无解,严重影响优化结果的可靠性[10-11]。目前基于多目标线性规划的农业水资源优化配置研究中,鲜有涉及到多目标权重不确定性方法的报道。因此,有必要引入能有效处理权重不确定性的多目标优化方法,提高优化结果的可靠性。其二,在考虑农业用水的生态目标时,大部分研究往往仅从减少农业用水量的角度来保证生态用水量,即关注农业用水优化配置的间接生态效益,而忽视了作物自身的固碳效应等直接的生态服务功能和价值。农田生态系统是一个巨大的碳汇系统,在碳的增汇减排中占有重要地位和作用[12-14]。农田生态系统具有巨大的固碳潜力,它对于区域及全球气候变化都具有积极影响。除此之外,农业生态系统中较高的碳循环水平可以有效增加土壤中有机质的含量并减少化肥的使用,这对于水土保持、缓解土壤沙化以及环境保护等均具有重要作用[15-16]。通过优化作物种植结构,有望在优化配置农业用水的同时,增加碳汇量、最大限度地发挥农田系统的生态功能。
因此,本研究靶向多目标权重不确定性难题,建立基于鲁棒规划方法的农业水资源多目标优化配置模型(Multi-objective robust programming model for agricultural water management with uncertain weights,MRPWU)。MRPWU 模型可以有效地处理权重中的复杂不确定性信息,并提供效益及风险定量化的优化方案。在优化目标中,以作物的碳汇价值表征农作物的生态功能、衡量种植对当地生态系统的正面影响。并且,将MRPWU 模型方法应用于水资源短缺、生态环境脆弱的甘肃省民勤县进行实例研究,产生作物种植结构调整的优化方案,为当地农业水土资源的高效利用提供参考方案和决策支持。
2 基于鲁棒规划的多目标优化方法
在农业水土资源优化研究中,通常面临着经济效益和生态效益协同提升的问题。多目标线性规划方法,可以有效地协调多个目标之间的权衡问题。但是,在决策过程中各目标的权重受决策者主观偏好等因素的影响,普遍存在着不确定性。传统的线性加权的方法,难以处理权重参数的不确定性信息。为了弥补水资源优化决策研究中多目标线性规划方法的不足,本文将基于鲁棒规划的多目标优化方法引入到水资源优化研究中,建立MRPWU 模型。该方法可以有效地处理双目标规划中权重的不确定性,在权重不确定条件下提供具有较高可靠性的结果。MRPWU 模型的一般式可表示如下。目标函数:

约束条件:


MRPWU模型的求解过程主要分为三个步骤。第一步,基于线性加权方法将双目标函数转化为单目标函数。第二步,引入保护函数,实现对不确定权重的保护程度和系统的风险水平的调控。第三步,将非线性的保护函数转化成为线性形式。经过以上三步,将包含不确定性权重参数的多目标规划问题转化为便于计算的线性的单目标形式。
具体而言,第一步,首先在目标函数中引入权重,表示各目标的重要程度[17]。通过线性加权的方法,将多目标转化为单目标:

式中:λ1和λ2分别为两个目标函数的权重。λ1和λ2均为正数,两者相互独立,且和为1。若同时处理两个权重的不确定性,两个权重参数很可能会相互影响。因此,需要对权重系数进一步转化。将两个权重系数同时除以λ1,得到修正后的权重λ'1和λ'2。其中,λ'1为1 并且始终保持不变,λ'2=λ2λ1。在之后的模型中,仅考虑λ'2的不确定性[18]。不论λ'2如何变化,原始的权重系数之和始终为1。因此,单目标函数可以转换为:

由于不同的目标函数具有不同的量纲,需要将不同的目标函数进行标准化处理[19]。标准化后的目标函数可以表示为:
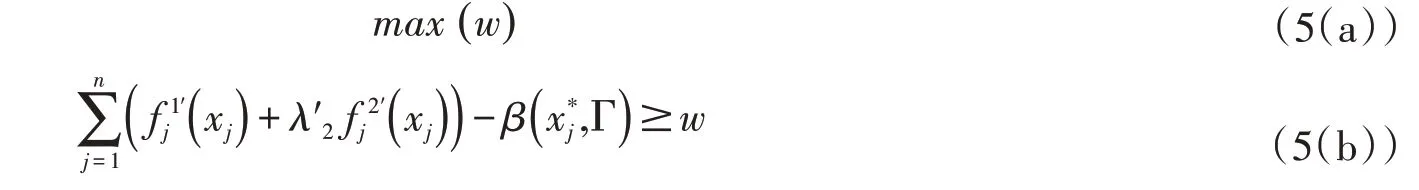
第三步,将保护函数转化为线性形式。通过对偶变换,求得该模型的对偶形式,将保护度函数转化为线性形式[18-19]。最终,得到式(5(b))等价的线性形式:
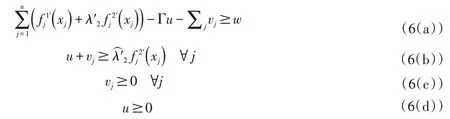
式中:u和vj是对偶变换引入的辅助变量。通过上述三步的转换,模型(1(a)—1(d))最终转换为易于求解的单目标线性规划问题。转换后的线性模型可以表示为:

约束条件:

3 实证应用
3.1 研究区概况与数据收集民勤县位于河西走廊东北部,石羊河流域的下游。年均降水为110 mm,而蒸发量却高达2644 mm,是典型的大陆性荒漠气候。农业是民勤的主导产业,境内有昌宁、环河和红崖山三个主要的灌区,见图1。昌宁和环河灌区的总种植面积分别为0.13 万hm2和0.27 万hm2,灌溉完全依靠地下水。红崖山灌区总种植面积为3.24万hm2,是民勤县最大的灌区,用水量占到总用水量的90%以上。红崖山灌区采用地表水和地下水联合灌溉的方式,石羊河为其提供了一定的地表水来源[23]。
随着当地的经济发展,灌溉用水量不断加大,导致地表水和地下水的过度利用。同时,不合理的种植结构,如大面积种植春小麦等高耗水作物,进一步加剧了当地水土资源的消耗,造成水资源短缺和沙漠化等生态问题[6,24]。因此,亟需加强农业水资源的合理高效利用,以缓解当地的水资源供需矛盾、促进生态环境的改善,从而实现可持续发展。
民勤的主要作物为小麦、玉米、棉花、向日葵和蔬菜。表1为五种主要作物的基础数据,这些数据来自民勤县统计年鉴、政府报告、规划文件、实地调研和相关研究[12,25-27]。规划期内,假设作物产量、价格以及成本等参数随时间稳步增加,灌溉需水量保持不变。考虑农艺技术的发展,年产量增幅为1.005;价格与成本的变化源于研究区多年资料,年变化率分别为1.1和1.05。农业的多年地下水与地表水可用水量保持稳定,年际间无明显差异。基于耕地红线确定最大种植面积,参考历史最低种植面积确定最小种植面积,复种指数取1.28。参考研究区多年作物产量、种植习惯及产业规划,确定粮食需求的上下限[28-29]。
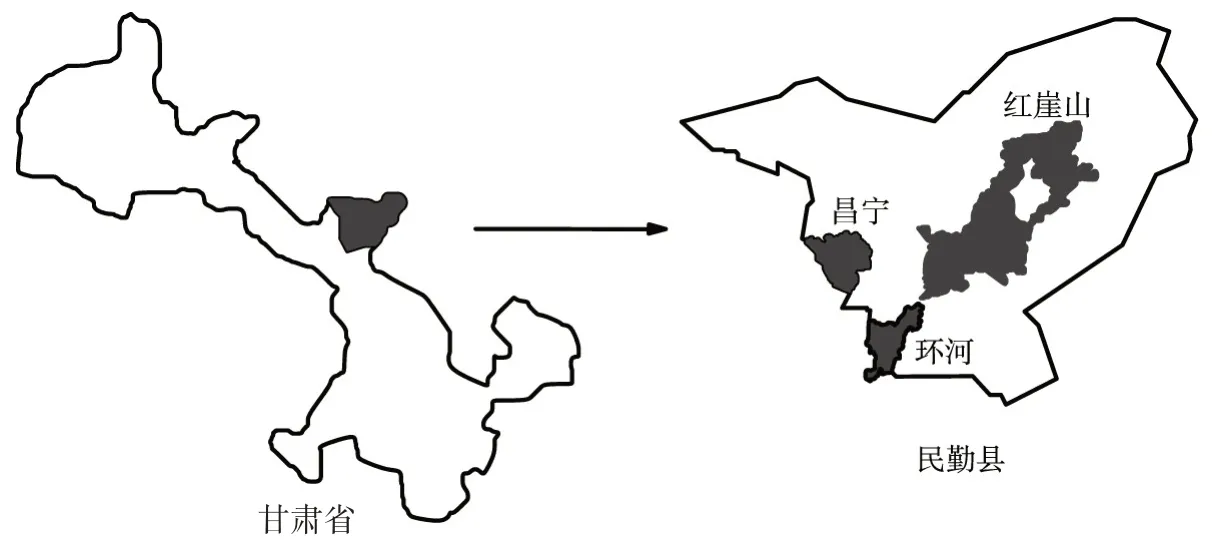
图1 研究区示意图
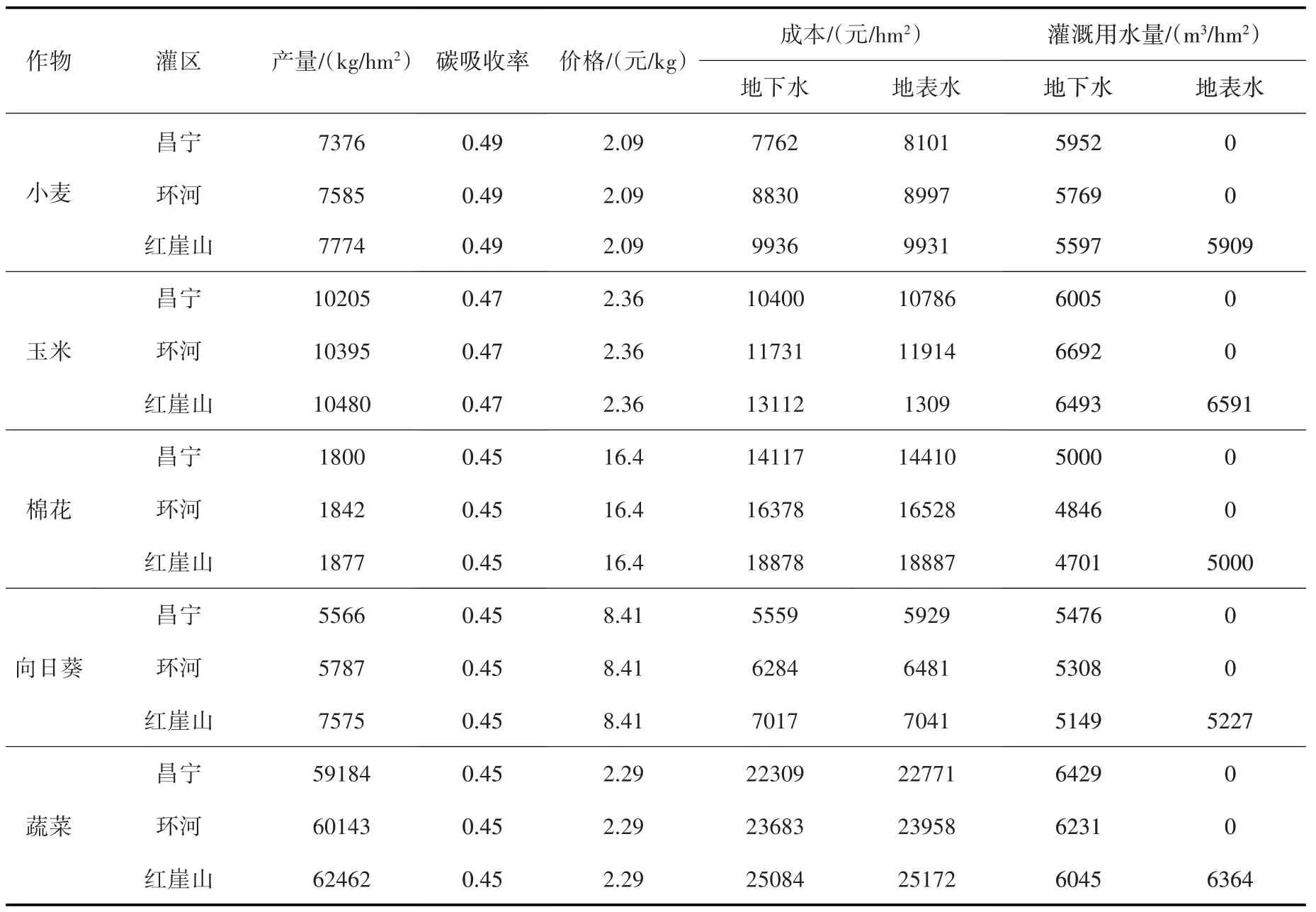
表1 研究区基础数据(2017年)
3.2 模型构建根据研究区的实际,为权衡农业生产中的经济和生态效益,构建了适用于民勤地区的MRPWU模型。目标函数是最大化经济和生态效益,其中经济效益是农业种植的净效益;生态效益以碳汇量衡量,作物本身的固碳潜力对于区域水土保持、缓解土壤沙化等均具有重要作用。根据不同种类作物的经济系数和碳吸收率,测算作物生育期内的碳吸收情况,计算得到每种作物的碳汇[30]。决策变量为作物种植面积Aijkt(hm2)。规划期是2017—2026年,以年为规划时段。目标函数的表达式如下:
(1)生态效益目标:

式中:i表示作物种类(i=1 表示小麦,i=2 表示玉米,i=3 表示棉花,i=4 表示向日葵,i=5 表示蔬菜),j表示灌溉水源(j= 1 表示地下水,j= 2 表示地表水),k表示子灌区(k= 1 表示昌宁灌区,k=2 表示环河灌区,k=3 表示红崖山灌区),t表示规划时期(t=1,2,…,10)。表示时期t子灌区k种植作物的生态效益,kgC;ei表示时期t作物i的碳吸收率,%;YIit表示时期t作物i的单位产量,kg/hm2;r表示时期t作物i的经济产品部分的含水量,%;HIi表示时期t作物i的经济系数。
(2)子灌区经济效益目标:

式中:表示时期t子灌区k种植作物的经济净效益,元;Pit表示时期t作物i的单价,元/kg;Cijt表示时期t作物i利用水源j灌溉的单位综合成本,元/kg,包括耕种、灌溉、施肥、施药等过程中的资源、材料购买和人力成本等。
约束条件:
(1)水资源总量约束:

式中:IRijt表示时期t作物i利用水源j的灌溉水量,m3/hm2;TAt表示时期t农业总可用水量,m3。
(2)地下水量约束:

式中:GWkt表示时期t子灌区k的农业可用地下水总量,m3。
(3)红崖山灌区地表水量约束:

式中:SWt表示时期t红崖山灌区的农业可用地表水总量,m3。
(4)昌宁、环河灌区不利用地表水:

(5)子灌区总种植面积约束:

式中:γ表示复种指数;表示时期t子灌区k的总种植面积下限,hm2;表示时期t子灌区k的总种植面积上限,hm2。
(6)粮食需求约束:

(7)非负约束:

4 结果分析
在构建的MRPWU模型中,生态效益与经济效益目标的初始权重分别取0.71与0.29。初始权重通过专家咨询的方式确定,将咨询后得到的平均值作为目标权重的名义值。修正后的目标权重分别为1.00 和0.41。为量化权重参数的不确定性程度对结果的影响,结合专家估值的数据分布情况,考察了一高一低两个权重值波动水平,即波动半径为 的50%(PEC50)或30%(PEC30)。考虑当地决策者对目标风险的接受程度,保护度水平D取值为D3、D6 或D9,对应保护不超过10%、20%和30%个子目标的权重[18]。在不同波动范围和保护度水平组合的情景下,分别对MRPWU模型进行求解,并得到不同情景的农业水资源优化配置方案,探究保护度水平和波动范围变化对模型结果的影响。情景设置如表2所示。通过对比情景1,2和3,探究保护度水平的改变对模型结果的影响;对比情景1和4,分析权重参数的不确定程度对模型结果的影响。
情景1下的作物种植结构优化方案如图2所示。小麦和向日葵的种植面积随时间下降,小麦的年生态效益和经济效益在各时间段内无明显变化。向日葵的年经济效益略有上涨。玉米种植面积先增长后下降,在第2 个时间段达到峰值1.05 万hm2。棉花和蔬菜都具有较高的单位生态效益,棉花的种植面积随时间增长,在第6个时间段后保持稳定。蔬菜种植面积随时间有小幅度下降,但在第6个时间段后不断增加、最终达到6387 hm2。作物种植面积随时间的变化与作物的单位效益、产量和价格等参数的变化有关,还受到约束条件变化的综合影响。作物在规划期内的种植面积比例如图3所示。玉米的种植面积最大,其次为向日葵、蔬菜和棉花,小麦的种植面积最小。

表2 情景设置
图4展示了各灌区灌溉水源的变化情况。以情景1为例,三个灌区全部规划期内的总种植面积为36.37万hm2。地表水为主要的灌溉水源,灌溉面积占总灌溉面积的68.6%。其中红崖山灌区的种植面积最大,地表水和地下水灌溉面积分别占该灌区总灌溉面积的77.1%和22.9%。
情景1 中,研究区生态效益与经济效益逐年增长,如图5 所示。第1 个时间段碳吸收量达到3.1×108kgC,经济效益为11.6亿元。随后,生态效益与经济效益分别以每年1.1%和0.7%的增速增长。第6个时间段之后,生态效益的增速开始放缓、降到0.46%,但经济效益的增速达到2.8%。结合图2(c)(e)可知,这主要是因为棉花种植面积保持稳定、导致生态效益的增长放缓,同时蔬菜的种植面积开始增长、导致经济效益快速增长。
规划期内,总经济效益为12.3亿元,总碳吸收量为3.25×109kgC。各作物对总效益的贡献情况如图3所示。对生态效益和经济效益贡献最大的分别为向日葵和蔬菜。根据初始权重计算得到各作物单位面积综合效益,蔬菜综合效益最高,其次为向日葵、玉米、小麦和棉花。作物经济和生态效益贡献的比例与其种植规模大小并不一致。例如蔬菜的种植面积仅比小麦多4%,但经济效益比小麦高13.4%。玉米的种植面积最大,但仅贡献了10%的经济效益。同样的,综合效益的排序与种植面积并不匹配。蔬菜拥有最高的综合效益,但仅占总种植面积的15.7%。上述结果是通过模型对经济和生态目标进行复杂的权衡,考虑作物的经济、生态影响以及水土资源的可利用性之后,通过自动寻求得出的。这也进一步说明,MRPWU 模型不但可以平衡不同目标之间的复杂权重,还能充分反映现实中的制约条件和种植习惯。

图2 情景1下作物种植面积优化方案(MRPWU:MRPWU模型结果;DEM:DEM模型结果)
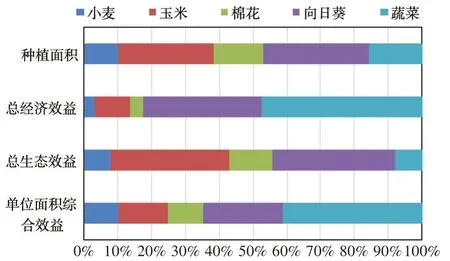
图3 情景1中不同作物对总种植面积、经济效益和生态效益的贡献率
上文描述了MRPWU 模型在波动半径为PEC50、保护度水平为D9(情景1)时的优化结果。而保护度水平与波动范围变化将会对模型结果产生较大的影响。其中,保护度水平表示受保护的权重的数量。为探究保护度水平对模型结果的影响规律,在相同的波动半径条件下,将保护度水平为D3(情景2)和D6(情景3)条件下的优化结果与情景1 进行比较。随着保护度水平的下降,情景2 和3 中地下水灌溉面积都不断减少。与情景1 相比,情景2 中昌宁、环河灌区无明显变化,红崖山灌区地下水灌溉面积下降了9499 hm2,地表水灌溉面积增加了8311 hm2。在情景3中,红崖山灌区地表水的变化趋势略低于情景2。对于不同作物而言,蔬菜的种植面积随保护度水平变化最为剧烈。情景2 中,蔬菜种植面积相比于情景1 提高了17.8%。玉米和棉花种植面积分别下降了4.7%和12.9%;小麦和向日葵的种植面积则没有明显的变化,对保护度水平的变化不敏感。相比于情景1,情景2 时的经济效益提高了7.7%,生态效益下降了1.9%,综合效益提高了3.9%。情景3 中,经济效益相比情景1 提高7.3%,生态效益则降低1.6%,综合效益提高了3.7%。随着保护度水平的提高,优化方案对应的加权后的综合效益降低,应对风险的能力相应提高,优化结果趋于保守。具体而言,经济效益随着保护度水平的增加而降低,生态效益则不断提高。虽然较低的保护度水平可以得到更高的综合效益,但同样需要承担更高的风险。保护度水平,可以根据研究区应对风险的能力和决策者对风险的接受程度进行综合判断;也可以在初步拟定多个保护度水平、得到模型结果后,根据实际情况,通过对比筛选得到最适宜的决策方案。
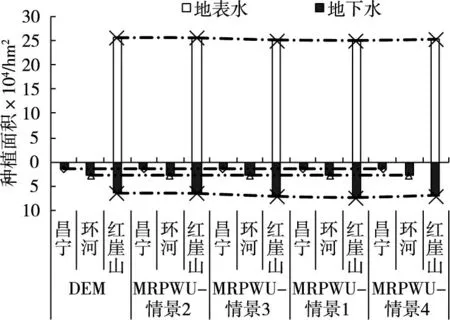
图4 各灌区分水源灌溉面积
波动半径代表了模型不确定权重变化的范围的大小,直接受到数据质量的影响。为探究权重波动范围对结果的影响,将波动半径为PEC30(情景4)的优化结果与情景1 进行比较。相比于情景1,情景4 中地表水依然是主要灌溉水源,地表水灌溉比例上升了1.3%,地下水则下降了4.6%。以棉花为例,情景1中棉花仅采用地下水灌溉。而情景4中,棉花在前两个时间段内联合利用地表水和地下水混合水源作为主要灌溉方式,第3到第6个时间段仅采用地下水,随后恢复到同时使用两种水源灌溉、且比例保持稳定。随着波动半径的缩小,情景4下的经济效益更高,生态效益则有所下降。相比情景1,情景4的总经济效益提高7.5%,生态效益则降低1.8%,综合效益提高6.0%(图5)。同时,规划期内情景4的生态效益与经济效益始终保持1.0%和0.8%的增速。在更低的波动半径条件下,决策可以得到更高的综合效益。这是由于在相同的保护度水平下,低波动半径中权重参数的不确定性较低,因此模型结果的效益更高。波动范围可以根据权重的数据质量设定。在初步确定权重时,如果决策者的犹豫程度较小,或者多位决策者的意见较为统一,对应于权重的波动半径较小(PEC30)的情况;反之,则对应权重波动半径较大(PEC50)的情况。在实际应用中,可以根据决策者对权重判断的肯定程度衡量决定,或者首先通过多种方式确定初始权重值、再根据初始值的波动情况,设置权重的波动范围。
5 讨论
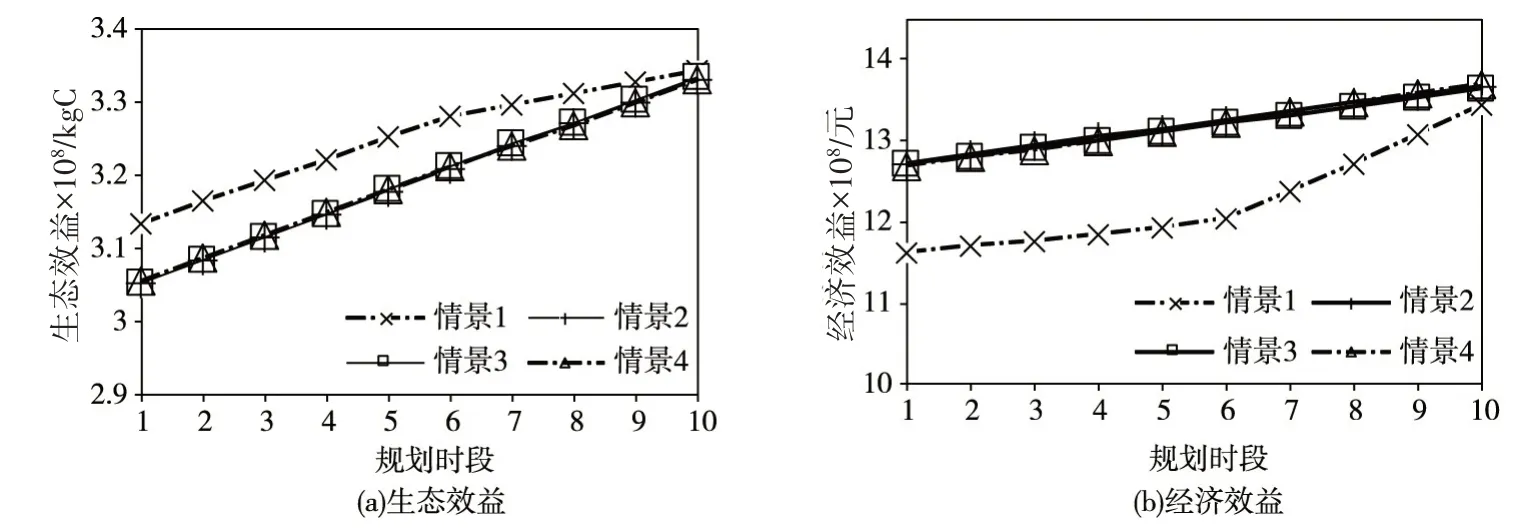
图5 规划期内的总生态效益和总经济效益
本文还利用传统的确定性权重线性加权方法,对构建的模型(8)进行求解,简称为权重确定性模型(DEM 模型)。DEM 模型中,目标函数的权重分别为MPRWU 模型的初始权重λ'1和。计算不同优化方案的得分值,综合评测DEM 和MPRWU 模型提供的决策方案。各方案的得分,通过标准化后的目标值乘以对应的修正后初始权重得到。其中,λ'2分别取确定性权重波动区间的上限值和下限值通过比较和分析在面对不同权重时优化方案的得分情况,对MPRWU模型优化方案的可靠性进行验证。
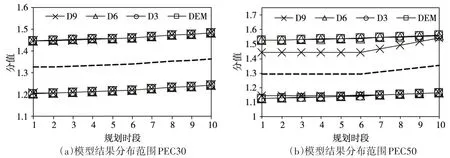
图6 MRPWU模型与DEM模型可靠性对比
MRPWU 模型和DEM 模型结果得分如图6 所示。当波动半径为PEC30 时(图6(a)),不同保护度水平下的得分的变化并不明显。当波动半径为PEC50 时(图6(b)),MRPWU 方案的得分比DEM 方案变化范围更小。而且随着保护度水平的增加,MRPWU 方案得分的范围也越小,即方案表现得更可靠。这是由于MRPWU模型中部分不确定权重参数受到保护函数的限制,目标函数在求解过程中受到更低的不确定性影响,模型结果更加可靠。
以情景1 为例,将MRPWU 模型与DEM 模型的结果进行比较。与DEM 模型结果相比,MRPWU模型的总生态效益增长1.9%,总经济效益降低7.1%,综合效益降低了3.7%。从经济和生态效益的角度而言,MRPWU 模型结果能够促进生态效益的提高,并且放缓经济目标的提升,这将会对民勤地区的生态系统产生更积极的影响。从种植结构角度看,MRPWU 模型相比DEM 模型总种植面积减少3.0%,农业用水量降低3.4%,地下水的灌溉面积有所增加。其中玉米的种植面积显著提高。棉花超过蔬菜成为第三大作物,小麦和向日葵的种植面积没有明显变化。由于未来社会偏好可能会发生一定的变化,目标的权重并非定值。DEM 模型仅能处理权重为某一确定数值的情况,没有考虑权重可能的变化,所提供的方案在未来的实施中可能会面临更高的风险、方案的不可行性也随之增加。MRPWU 模型则充分地考虑了权重变化的情况。相比较于DEM 模型,MRPWU 模型提供的优化方案虽然更为保守,但模型的鲁棒性和应对风险的能力也得到提高,可以提供更加可靠的模型结果。
在实例研究中,不同情景下MRPWU模型与DEM模型的比较结果显示,相比于其他情景,情景1的模型结果更可靠、生态效益更高;虽然综合效益有所降低,但仍在可接受范围内。因此将情景1作为研究区当前的推荐情景。推荐情景也并非固定不变,具体设置随着研究区及其决策者实际情况而变化。将MRPWU模型应用到其他场景时,可以根据决策者对风险可接受程度确定保护度水平,根据权重的数据质量设定波动范围。
此外,将MRPWU 模型情景1 的优化结果与2017年的实际情况进行了比较。2017年作物总种植面积为3.62 万hm2,灌溉用水2.15 亿m3,经济效益达到1.27 亿元。与之相比,MRPWU 模型的优化结果中,研究区经济效益和综合效益分别降低了8.5%和2.2%,生态效益提高了1.6%。蔬菜等高经济效益作物的种植面积逐渐降低,转而发展以玉米为主的粮食作物,在保证粮食稳定供给的同时提高了生态效益。当前民勤过多地种植了蔬菜而忽视了玉米和棉花。作物种植结构的调整,可以促进当地均衡发展与生态环境修复。从总量看,总种植面积和农业用水量分别下降了1.6%和1.9%。若把节省下来的土地和水资源用于生态修复或森林种植,将对研究区域生态可持续发展产生更深远的影响;如果把节省下来的资源用于其他行业,也可弥补因种植结构优化而损失的经济效益。在实际生产中,MRPWU 模型可以帮助决策者制定作物种植结构的整体规划,决策者可以根据整体规划,结合土地条件、投资成本和种植习惯等因素,有倾向性的制定农业种植计划。
6 结论
本研究针对农业水资源多目标规划中存在的权重不确定性难题,建立了基于鲁棒优化方法的农业水资源多目标优化配置模型(MRPWU)。通过引入鲁棒优化方法,对多目标规划问题中权重的不确定性进行了处理。MRPWU模型通过引入保护函数这一机制,降低了权重值的改变对模型输出产生的影响、提高了模型抵抗权重不确定性波动的能力,实现对模型的最优性和鲁棒性之间的权衡和调控,为解决复杂不确定条件下的农业水资源配置问题提供方法支撑。
以水资源短缺的西北旱区甘肃省民勤县为研究区,进行实证研究。以经济效益和生态效益最大为目标。其中,生态效益用作物碳效应进行量化。同时,MRPWU 模型提供了在不同的波动半径和保护度水平组合下的决策方案。结果表明,蔬菜、向日葵分别贡献最大的经济效益和生态效益,同时蔬菜具有最高的综合效益。向日葵和玉米的种植面积最大。随着保护度水平的提高、或权重不确定性程度的增加,生态效益将上升,经济效益和综合效益将略有下降,优化结果面临的风险也随之下降。提高保护度水平,意味着决策方案更保守、决策风险更低。在实际应用中,决策者可以根据对风险的接受程度和数据质量,确定波动范围和保护度水平,进而得到最适宜的决策方案。
对比不同初始权重时MRPWU 模型和DEM 模型优化方案的综合得分情况,证明MPRWU 模型可以在权重复杂不确定条件下提供更加可靠的优化方案。相比于DEM 模型,MRPWU 模型产生的综合效益下降了3.7%,但是其优化方案能够降低系统风险,也更为可靠。相比于2017年的实际情况,MRPWU 模型通过提高玉米、棉花的种植比例,使研究区生态效益提高1.6%,种植面积减小1.6%,同时减少灌溉用水量3.9%。
