水沙两相浑水模型的紊流封闭及初步验证
2020-05-21张红武钟德钰
黄 海,张红武,张 磊,钟德钰,3
(1. 清华大学 水沙科学与水利水电工程国家重点实验室,北京100084;2. 中国水利水电科学研究院 泥沙研究所,北京100048;3. 青海大学 三江源生态与高原农牧业国家重点实验室,青海 西宁 810016)
1 研究背景
由于复杂的固液相间作用和颗粒碰撞等机制的影响,挟沙水流的紊流特性比清水要复杂得多。在早期,受挟沙水流紊动认识的限制,张红武[1-2]、Johansen[3]、Greimann 等[4]、Toorman[5]和钟德钰等[6-7]采用经验或半经验公式对固、液相的紊动变量进行计算,但都存在一定的局限性,只能适用于恒定均匀的低含沙水流。鉴于此,Oliveira 等[8]、Jha 等[9]和Chen 等[10]采用不同形式的单相k-ϵ模型对液相的紊动变量进行计算,对于固相紊动变量通过建立其与液相紊动变量的代数关系进行确定。然而,挟沙水流紊动与清水明显不同,泥沙对挟沙水流紊动强度有显著影响,目前学术界主要存在三种观点,即紊动增加[11]、紊动减小[12]和紊动不变[2]。泥沙对挟沙水流紊动既有促进的因素,又有抑制的因素,紊动变化是多种因素综合作用的结果[13]。因此,清水k-ϵ模型结合固相经验公式的方法只能适用于低浓度的、颗粒粒径较小的挟沙水流,在这种情况下固液相间作用才可以被忽略。
对于冲积河流而言,泥沙颗粒与水流的几何特征尺度相比都比较小,因此,当挟沙水流的泥沙浓度不是非常低,水沙两相流的系综平均成立的条件下,水流中运动的泥沙和挟带泥沙运动的水流都可以看作连续介质,此时,挟沙水流是一种典型的固液两相流[7]。因此,近些年来一些学者采用双流体紊流模型对挟沙水流控制方程中的紊动变量进行封闭,取得了诸多成果。1980年代周力行等[14]提出了多相流领域的k-ϵ-kp、统一二阶矩和显式代数应力模型,得到了国内外的广泛应用。倪浩清等[15]考虑了浮力流、回流及旋流的作用,修正了统一二阶矩两相湍流模型中的颗粒质量脉动输运方程,提出了改进的湍流双流体模型,将其应用于悬沙冲淤问题。当双流体紊流模型应用于较高颗粒浓度的情况,要考虑颗粒之间的碰撞。Hsu等[16]结合了k-ϵ-kp模型和稠密气体动理学理论的结果,对含沙量较高的挟沙水流进行模拟。Peirano 等[17]基于颗粒流动理学理论的结果,建立了同时考虑液相和颗粒湍流以及颗粒碰撞的双流体紊流模型。Longo等[18]的双流体紊流模型进一步考虑了非弹性碰撞的影响。双流体紊流模型可以考虑相间紊动量传递、颗粒浓度、颗粒碰撞以及颗粒惯性的影响,而受到人们关注。但是,对于双流体紊流模型而言,考虑到固、液相各自的质量、动量、紊动能和耗散方程,巨大的计算量是实际应用的一大障碍。
与多相流领域的关注点不同,河流泥沙领域并不太关注液体和泥沙颗粒各自的运动,而是更关心挟沙水流的宏观运动,不过同时又能反映出固、液相间作用以及颗粒碰撞等微观物理机制对宏观挟沙水流运动的影响。因此,有必要寻求一种新方法替代双流体模型。一些学者结合双流体模型的优势,并顾及泥沙研究的特点,建立挟沙水流的两相浑水模型(twophase mixture model),例如,Cao 等[19]、Wu 等[20]、Jha 等[9]和钟德钰等[6-7]提出了固液两相浑水模型,他们通过对固液两相的质量守恒和动量守恒方程分别相加求和,可以得到两相浑水的质量守恒和动量守恒方程。不同的固液两相浑水模型的控制方程基本相似,区别主要在于对固相漂移速度的封闭方法有所不同,封闭方法可分为:扩散模型[20]、漂移通量模型[21]、部分双流体模型[9]和弥散模型[6]。固液两相浑水模型把水沙混合物当作一个整体,同时可以考虑相间作用,而其偏微分方程的数量却只与清水的相同。近几年来,钟德钰等[6-7]用两相浑水模型对挟沙水流进行模拟,采用弥散模型对固相漂移速度进行封闭,固相漂移速度反映了沉积、扩散、颗粒自身紊动和颗粒间相互作用等物理机制,考虑因素全面,资料检验表明在较大的水流强度和含沙量变化范围内,只要固相漂移速度能够较精确地确定,两相浑水模型就能够较准确地计算出挟沙水流的流速和含沙量分布[6]。然而,其仍沿用双流体紊流封闭的思想,即对固、液相雷诺应力分别进行求解,再用经验或半经验公式[6-7]对固液相各自的紊动变量进行计算,这些经验或半经验公式大多是用实验数据拟合得到,只能适用于恒定均匀的挟沙水流。鉴于此,本文在两相浑水理论框架下,构建两相浑水紊流模型,将水沙混合物当作一个整体进行考虑,并反映出固液相间作用和颗粒碰撞等微观物理机制对挟沙水流紊动的影响,又使得两相浑水紊流模型的偏微分方程数量与传统紊流模型相同,且适用于一般条件下的挟沙水流紊动计算。
2 固液两相浑水雷诺应力的本构关系
两相浑水理论的质量守恒方程、动量守恒方程和固相体积分数方程分别表示如下[6-7]:
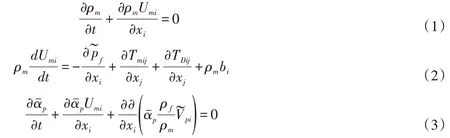
式中:分别表示两相浑水的密度和速度;为液体压强;为弥散应力张量,表示固、液相间作用对挟沙水流动量的影响;是漂移速度,其物理含义是颗粒相对于两相浑水的一种弥散现象,可通过钟德钰推导的漂移速度本构关系式计算[6-7];bi表示体应力;下标k=f表示液相,k=p表示固相,下标m表示两相浑水;、ρk和分别表示k相的体积浓度、密度和沿i方向的平均速度;“~”表示浓度加权平均;“-”表示系综平均值;Tmij为两相浑水应力张量,是液、固相应力张量的体积加权平均,其表示如下[7]:
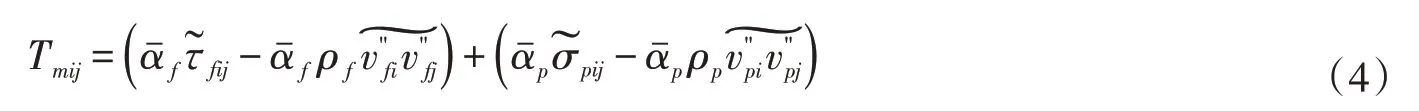
本文基于固液两相浑水理论的思想,将水沙混合物当作一个整体,直接对两相浑水雷诺应力构建本构关系,而不对固、液相雷诺应力分别进行计算。令表示两相浑水雷诺应力张量。通过固、液相雷诺应力张量的Boussinesq 展开式[17]求和,又因为两相浑水速度Umi为固、液相速度的0阶近似,可以得到:


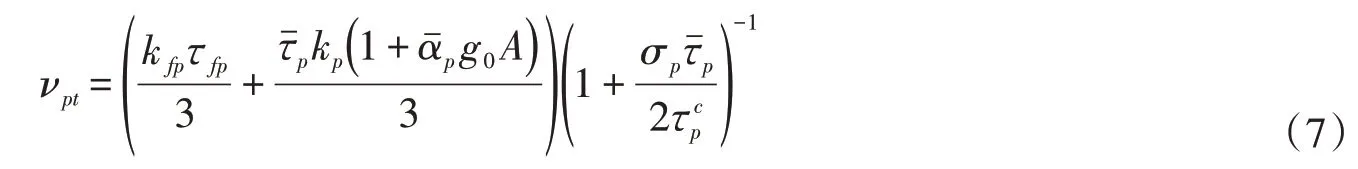
式中颗粒运动和水团紊动的相互作用时间τ fp表示为[17]:
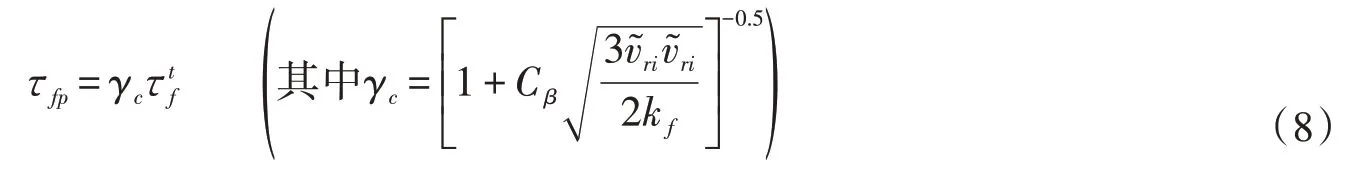
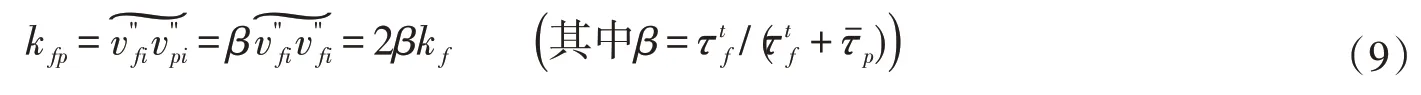
式(7)中的颗粒碰撞时间尺度表示单个颗粒相邻两次碰撞的时间间隔[17]:

式中dp表示颗粒粒径。将和式(7)代入式(6)得到:
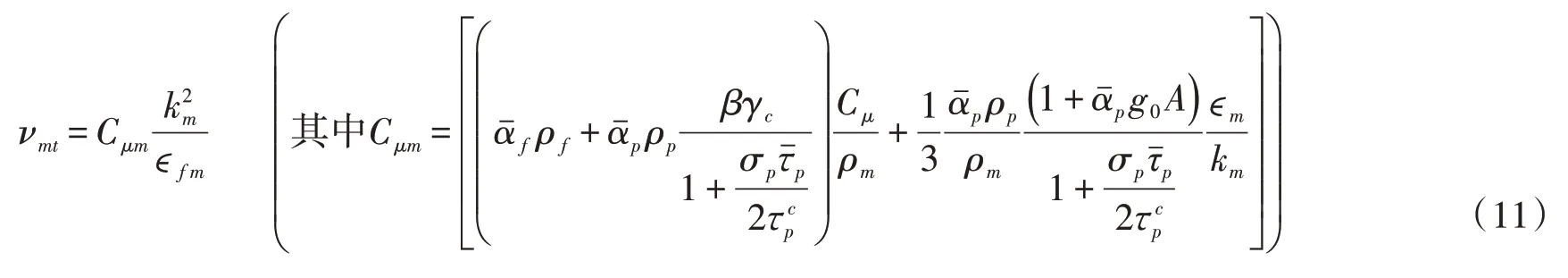
推导式(11)的过程中,用到kf≈km、ϵf≈ϵm和kp≈km的近似,这是因为,对于冲积河流而言,泥沙颗粒与水流的几何特征尺度相比较小,颗粒紊动特性受水流紊动主导。ϵm为两相浑水紊动耗散。
3 挟沙水流的固液两相浑水紊动和耗散方程构建
从式(5)和式(11)可以看出,只要求出两相浑水紊动能km和紊动耗散ϵm,以及固、液相的紊动能和紊动耗散(kf和ϵf,kp和ϵp),即可完成对两相浑水雷诺应力的封闭。基于双流体紊流方程推导两相浑水紊动能km和紊动耗散ϵm的输运方程,并通过引入固相偏移紊动能∆kp的渐近解以及构建固相紊动耗散ϵp的代数表达式的方法,对固、液相紊动能和紊动耗散进行求解。
3.1 固相紊动能和紊动耗散方程固相紊动能方程的推导过程:(1)固相总能量Kp=vpivpi/2 的方程可以通过固相瞬时动量守恒方程[7]乘以固相瞬时速度vpi得到;(2)固相平均能量的方程可通过Favre 平均的固相动量守恒方程[7]乘以固相平均速度得到;(3)固相紊动能方程可通过固相总能量Kp=vpivpi/2 方程减去固相平均能量方程得到:
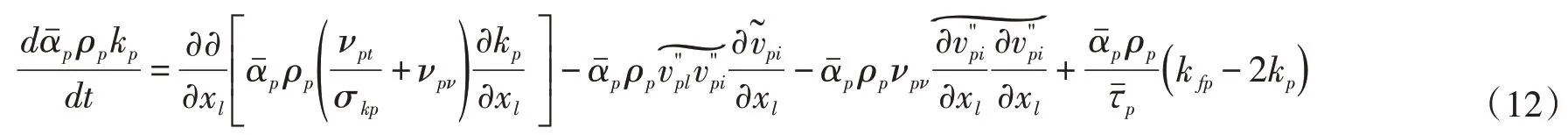
式中νpν为颗粒碰撞黏性系数可以采用颗粒流动理学结果进行计算[17],式(12)右端最后一项为固、液相间作用对固相紊动能的影响。
与清水紊动能耗散方程的推导过程相似,可以得到固相紊动耗散方程:
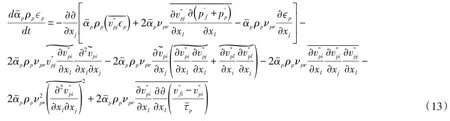
其中右端最后一项为相间作用对固相紊动能耗散的影响。类似于清水耗散方程的模化方法可得:
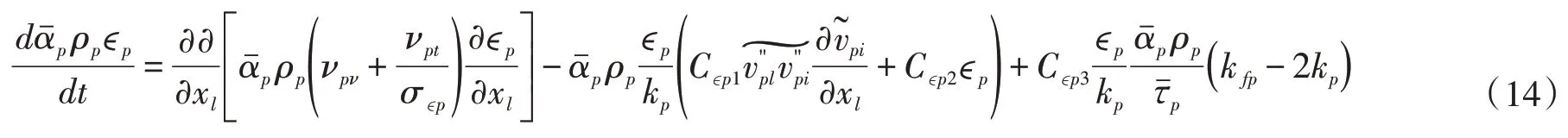
3.2 液相紊动能和紊动耗散方程类似的,液相紊动能方程和紊动能耗散方程也可通过上述推导方式得到:
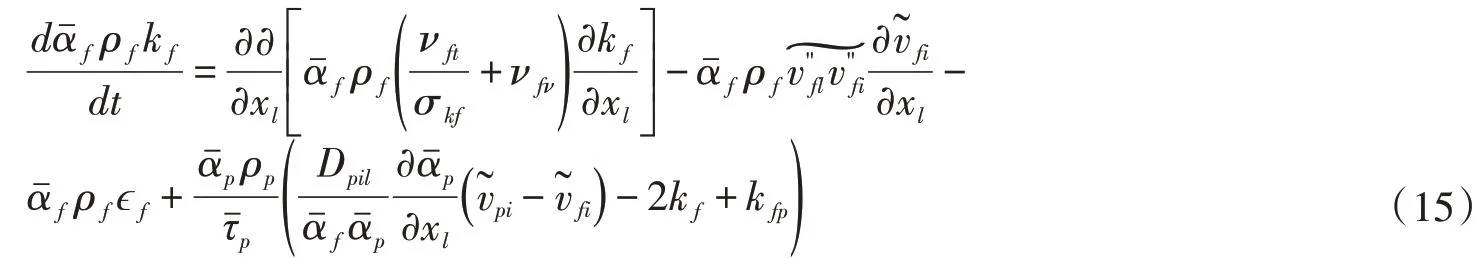

式中:νfν为液相黏性系数;Dpil为颗粒紊动扩散系数。
3.3 两相浑水紊流模型基于3.1 节和3.2 节的双流体紊流方程推导两相浑水紊流方程。两相浑水紊动能km输运方程可通过对固、液相紊动能方程式(12)和式(15)求和得到:

从式(18)可看出固、液相紊动能kp和kf均尚未封闭。本文引入偏移紊动能的概念对固、液相紊动能进行封闭。偏移紊动能∆kk表示k相紊动能对于两相浑水紊动能的相对偏差。中心思想是将k相紊动能进行如下分解:
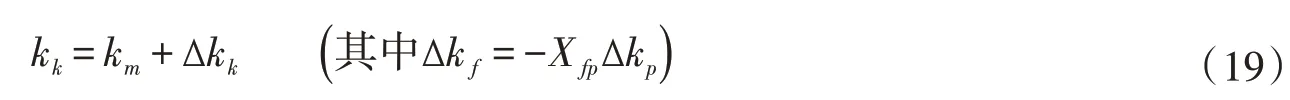
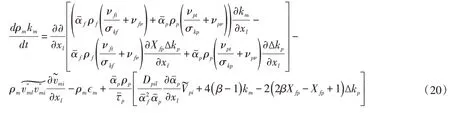
对于两相浑水紊动耗散ϵm的方程,可以通过对式(13)和式(16)进行求和,类似于清水紊动耗散方程的模化方法得到:
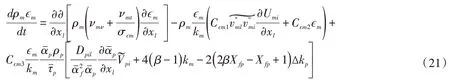
3.4 固相偏移紊动能的本构关系从式(20)和(21)可以看出,固相偏移紊动能∆kp是封闭两相浑水紊流基本方程的关键变量。固相偏移紊动能∆kp表示固相紊动能与固液两相浑水紊动能的相对差,可通过对固相紊动能方程采用摄动法求得其渐近解。通过引入特征长度L、特征速度U,固相紊动能方程中的自变量和因变量可以化成无量纲形式:
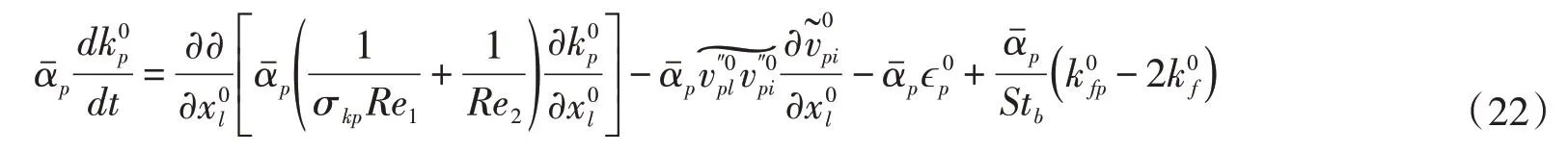
式中:Re1=UL/νpt;Re2=UL/νpν;Stb=τˉU/L是Stokes 数。若将固相紊动能用式(19)进行分解,且kfp采用式(9)计算,式(22)可写为固相偏移紊动能∆kp的偏微分方程:
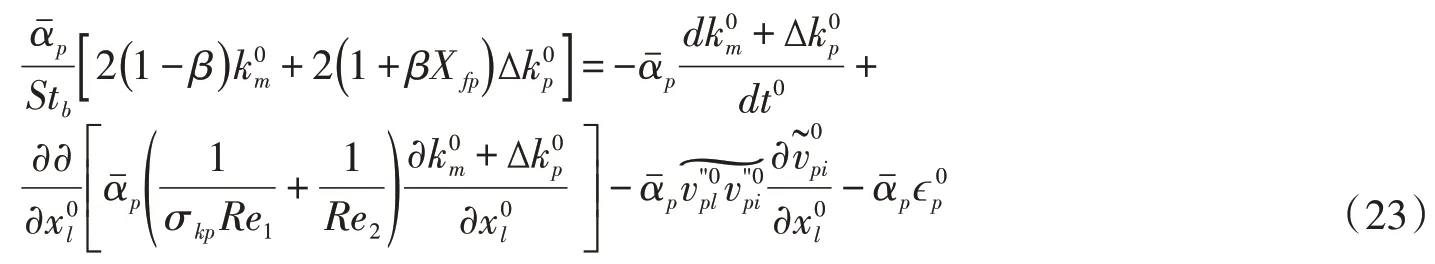
注意到式中Stb=τˉU/L反映颗粒运动对外力变化的响应时间尺度与水流特征时间尺度的比值[7]。对于明渠挟沙水流来说,颗粒的Stb通常是个小量,可采用摄动法来获得固相偏移紊动能的渐近解,将展开为Stb的指数多项式,经运算,可得到包含0阶和1阶近似项的表达式:
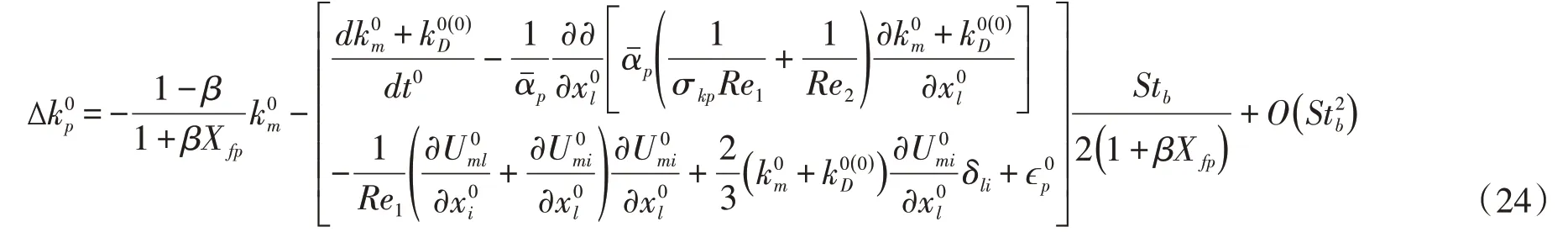
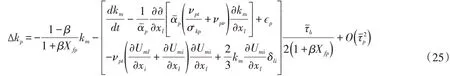
同理,两相浑水紊动能方程式(20)也可进一步化简为:

为代数求解式(25)还需对固相紊动耗散ϵp进行封闭。由于k-ϵ模式多适用于紊动变量随时间变化较慢的情况[23],为减少偏微分方程数量,忽略式(14)中的时间导数项可得:

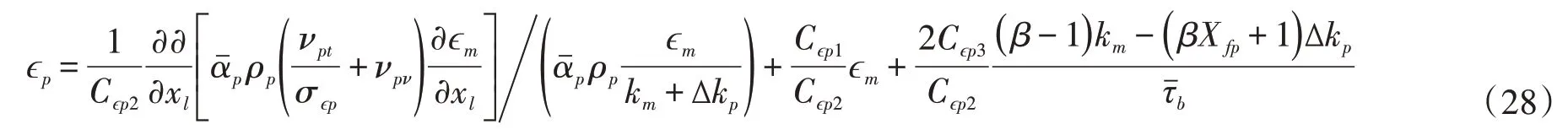
最终,式(5)、式(21)、式(25)、式(26)和式(28)构成两相浑水紊流模型的基本方程。模型中的参数设定为[17]:σkm=σkp=1,σϵm=σϵp=1.2,Cϵm1=Cϵp1=1.44,Cϵm2=Cϵp2=1.92 和Cϵm3=Cϵp3=1.2。
3.5 各向紊动强度分配系数本文模型与k-ϵ模式相似,尚无法给出各向异性的紊动强度,为与实测资料更好地比对,需要计算各向紊动强度。基于已有的实测资料[24],易知纵向紊动强度v"mx与挟沙水流紊动能具有如下关系:
纵向紊动强度

纵向紊动强度分配系数λx=1.05。根据张红武[1]的研究结果,垂向与纵向紊动强度具有如下关系:
垂向紊动强度

垂向紊动强度分配系数

式中Δ表示床面粗糙度。
3.6 边界条件为计算流速沿垂线分布,需要设定水面和底部边界条件,根据Graf[25]的明渠水流研究结果对底部和水面边界条件进行确定:

式中:u*为摩阻流速;κ=0.4为Karman常数;zb为床面计算单元的厚度。
本文采用张红武[26]的绝对浓度沿垂线分布公式确定近底处的含沙量边界条件:

式中:为垂线平均体积浓度;κm是两相浑水的卡门参数[26],ηa=a/h为参考点的相对水深;ωs为颗粒群体沉速[27]:
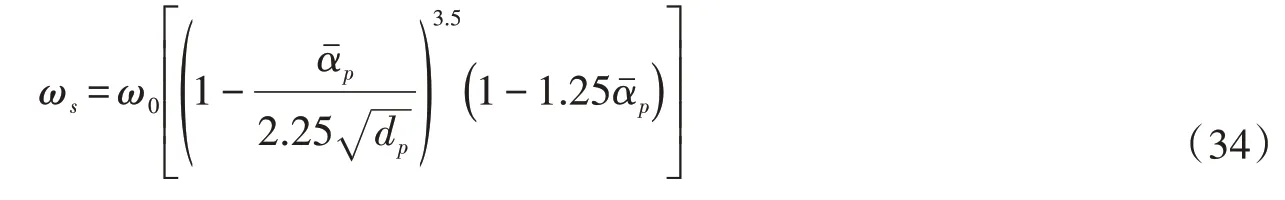
式中ω0为单颗粒在静水中的沉速。N0表达式如下[26]:
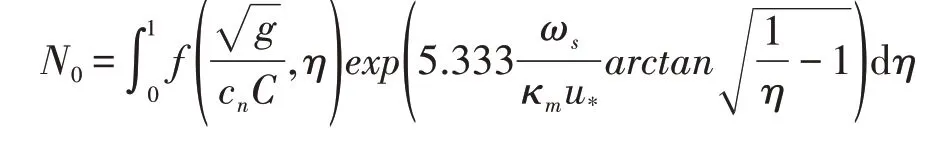
其中:

式中:C为谢才系数;η=y/h为相对水深;cn为涡团参数[26],cn=0.375κm。
紊动变量水底和水面的边界条件如下[28]:
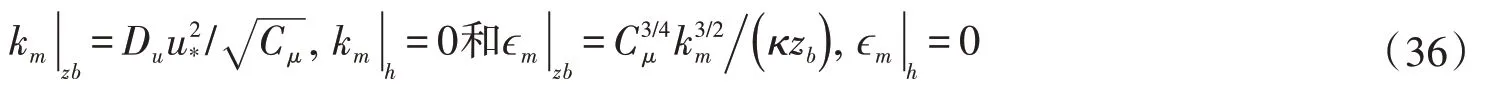
式中Du表示颗粒存在对床面紊动能的影响,该值列于表1 中。值得注意的是,Du值随着含沙量的增加明显减小,关于Du值的变化机制还需进一步研究。
4 模型验证
利用了Wang 和Qian[29]的实验资料在本文模型进行论证。实验在长直水槽中进行,水流条件为二维明渠恒定、均匀流。实验分为两组,分别采用密度为2.64 g/cm3、粒径为0.137 mm 的天然沙和密度为1.05 g/cm3、粒径为0.268 mm 的塑料沙作为悬移质。实验水流和泥沙特征参数见表1,表1 第一列表示各组实验的编号;h表示水深;u*表示摩阻流速;dp为泥沙中值粒径;κm表示两相浑水卡门参数;ρp表示颗粒相密度;ωs表示颗粒沉速;αˉpv表示垂线平均体积浓度;Stb表示Stokes 数;Du表示颗粒存在对床面紊动能影响的参数;δ表示从床面至最大纵向流速处的水层厚度。

表1 Wang等[29]实验的水流和泥沙特征参数
图1 给出了计算与实验的两相浑水纵向速度沿垂线分布和根据Nezu 等[24]的清水对数流速公式计算相同实验条件下的清水纵向流速沿垂线分布。图1中也绘出在相同实验条件下采用本文模型计算的清水纵向流速沿垂线分布以供对比。从图1可看出,本文模型能够很好地模拟实验中各组水流速度的分布。两相浑水速度梯度相较于清水的速度梯度有所增大,且随着含沙量的增加,增大的程度更为显著。需要说明的是,在水面附近,两相浑水纵向速度的计算值与实测值存在一定偏差,原因可能来自两个方面:(1)实验水槽宽深比较小,在水面附近区域水流受到边壁的影响,三维运动特征十分显著,而图中计算结果是在假设完全二维流动的条件下得到的,与真实的三维流动有差距;(2)真实水流运动受表面张力的影响,然而在本文模拟中并未考虑表面张力。误差的具体原因仍需进一步研究。
泥沙颗粒的滞后速度绘制于图2 中。滞后速度是指泥沙颗粒群的平均速度与液相平均速度的差。其与泥沙颗粒和液相的相对速度不同,相对速度是指单个泥沙颗粒与颗粒周围流体的速度差,Kiger 等[30]的实验结果表明单个颗粒与周围流体的速度非常接近,相对速度几乎为0,他们结合实验结果推断滞后速度可能的物理机制:在垂线方向上,存在浓度梯度和速度梯度,来自床面附近的低速水团携带较多的泥沙颗粒上升,远离床面的高速水团携带较少的泥沙颗粒下降,两种水团相遇掺混,混合水团中含有较多低速水团中的泥沙,含有较多高速水团中的水体,因此,混合水团中泥沙颗粒群的平均速度通常小于液相的平均速度,即为泥沙颗粒的滞后速度[6]。如图2 所示有以下几点结果:(1)泥沙颗粒的速度滞后于水流速度,且越接近床面,两者速度差越显著。(2)随着含沙量增加,塑料沙和天然沙相对于液相的滞后速度均减小。(3)泥沙颗粒的滞后速度与沉速为同一量级。
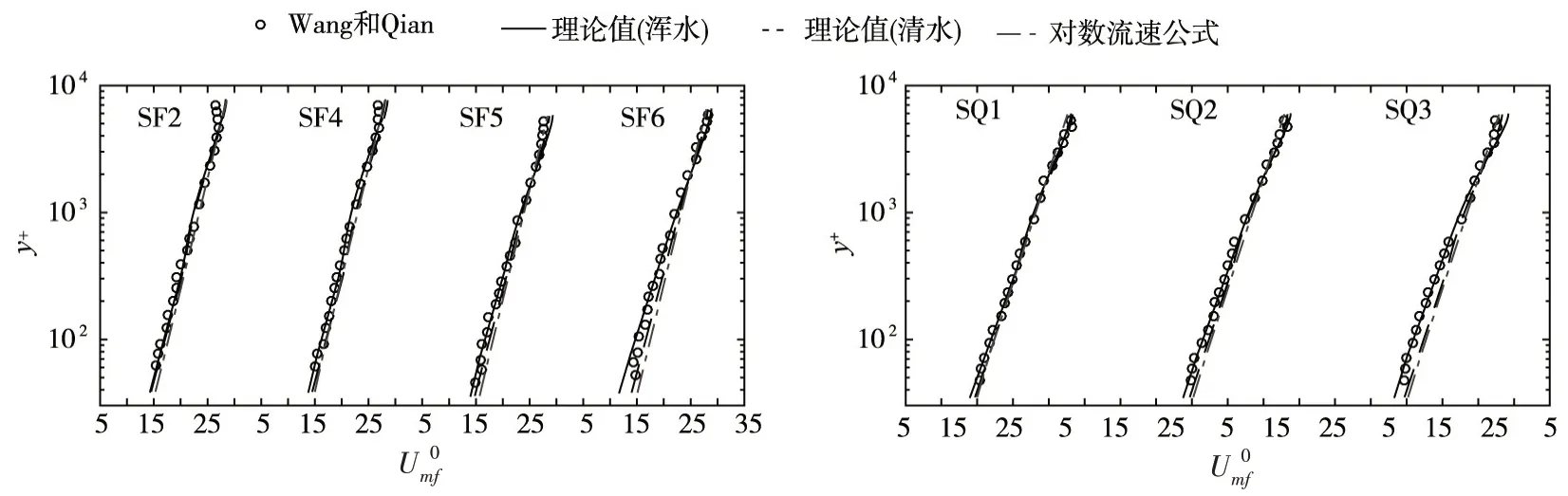
图1 纵向流速沿垂线分布的理论与Wang和Qian实验对比
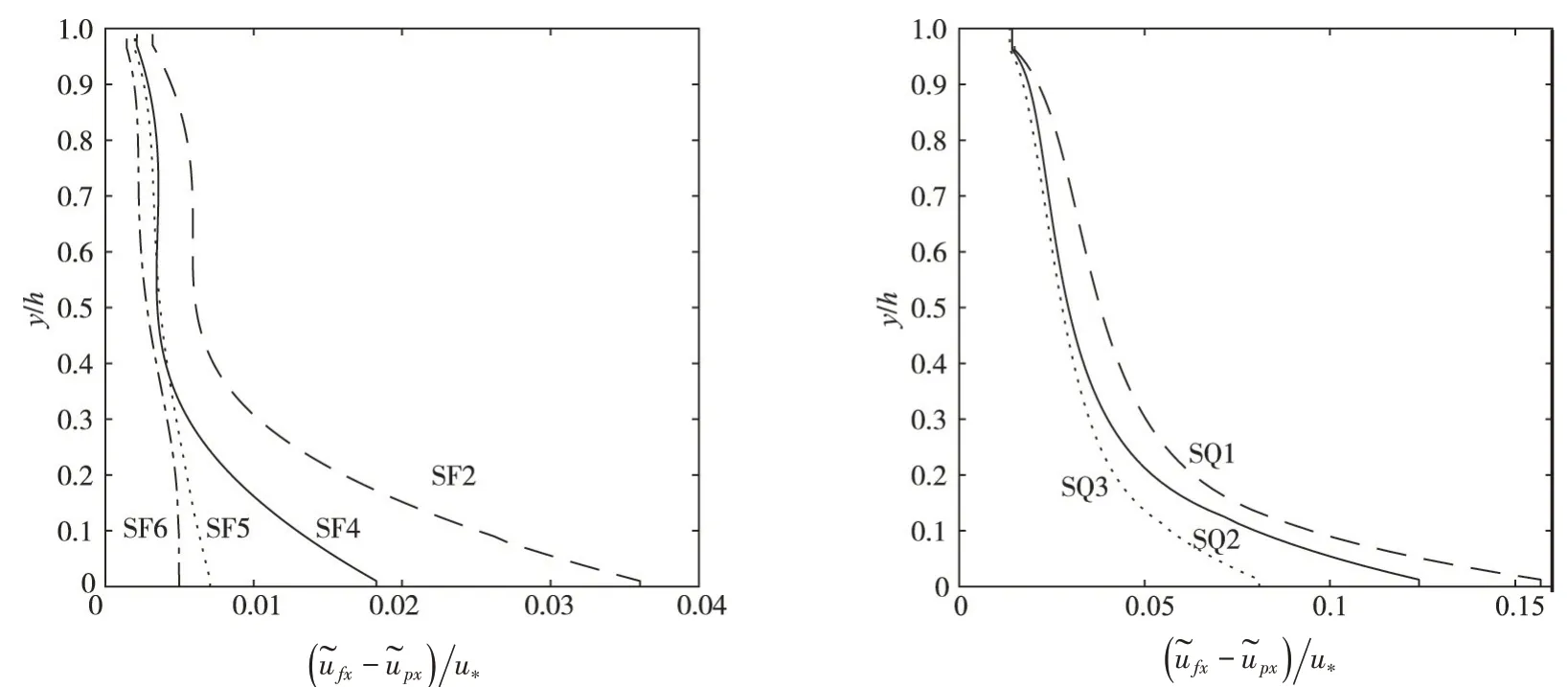
图2 泥沙颗粒滞后速度
图3给出了两相浑水模型和Rouse 公式[31]计算的浓度分布结果。在含沙量较低的SF2组,本文模型的计算值与Rouse 公式计算结果均与实测值符合较好,随着含沙量增加(SF4—SF6),Rouse 公式的计算结果与实测值有明显偏差,而本文模型的计算值仍与实测值符合较好。在SQ 组实验中,Rouse公式的计算结果与实测值有偏差,而本文模型的计算值与实测值符合较好。事实上,漂移速度~Vpi本构关系[6-7]充分考虑了影响泥沙悬浮的因素,包括:重力沉降、两相浑水紊动扩散、颗粒碰撞扩散以及颗粒紊动自扩散。在含沙量较高、颗粒惯性较大的条件下,由于本文模型对影响悬移质泥沙悬浮的因素考虑更为全面,能适用于更大的颗粒惯性和含沙量变化范围。钟德钰等[7]已对两相浑水紊动扩散、颗粒碰撞扩散以及颗粒紊动自扩散对悬移质泥沙悬浮的影响机理进行了充分的研究,详细内容可参考其专著的相关章节[7]。附带指出,本文对于悬移质含沙量验证是绝对浓度沿垂线的分布,比事先凑好底部参考点含沙量后再进行验证计算的做法要求更高,更具有实际应用价值。

图3 含沙量沿垂线分布的理论与Wang和Qian实验的对比
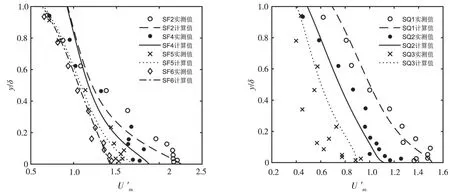
图4 纵向紊动强度的理论与Wang和Qian实验的对比
Wang 和Qian[29]对各组实验的纵向紊动强度也进行了测量,图4 给出了计算和实测的纵向紊动强度沿垂线分布。从图4可以看出:(1)本文模型计算得到的纵向紊动强度与实测结果基本相符。(2)随着含沙量的增加,紊动强度受到的抑制作用更强烈。
从图4可以看出,这两组实验条件下,颗粒存在抑制了挟沙水流的紊动。诸多学者将此归结于密度梯度的影响,并在清水k-ϵ模型中增加浮力产生项来反映密度梯度对挟沙水流紊动的影响[9]。尽管紊动水团需要克服密度梯度消耗紊动能量,但其对紊流变化的影响仅仅占很小一部分[7]。研究结果也证实了这一点,与天然沙实验相比,塑料沙在垂向上的分布更为均匀,密度梯度效应几乎可以忽略,然而从图4可以看出,颗粒对挟沙水流紊动仍有明显的抑制作用,因此,紊流调制不能完全归因于密度梯度。事实上,在充分发展的二维明渠恒定均匀流条件下,两相浑水紊动能方程式(26)可化为:
从式(37)可以看出,浮力项所表征的密度梯度只是导致挟沙水流紊动能变化的因素之一。固、液相紊动和颗粒碰撞导致挟沙水流紊动能的扩散;固、液相雷诺应力对平均流速场做功导致挟沙水流紊动能的产生;液相的黏性应力与颗粒碰撞黏性应力导致挟沙水流紊动能的耗散;固、液相间作用也会导致挟沙水流紊动能的变化。只有在模型中综合考虑上述机制对挟沙水流紊动的影响,才能反映出紊流调制现象。
5 结论
本文以双流体紊流模型及颗粒流动理学成果为基础,通过对固、液相紊动能方程和紊动能耗散方程分别进行求和,可得到两相浑水紊动能方程和紊动能耗散方程,采用摄动法可求得固相偏移紊动能的渐近解,在技术细节中采用Peirano 等[17]的颗粒流动理学结果计算固相紊动黏性系数来反映颗粒惯性的作用。采用紊流力学原理体现挟沙水流紊动的各向异性;采用河流动力学基本理论中绝对含沙量分布公式解决底部浓度边界条件,采用泥沙群体沉速公式解决固相浓度对颗粒在液相中沉降规律的影响。最后构建两相浑水紊流模型,偏微分方程数量较双流体紊流模型减少一半,考虑了固、液相间作用和颗粒碰撞等复杂微观机制对挟沙水流紊动的影响,不仅能够计算出两相浑水紊动能,还能够计算出固、液相各自的紊动信息。实验资料验证表明,在较大的浓度变化范围内,两相浑水紊流模型计算结果与实测结果相符,能够定量计算出挟沙水流紊动随着含沙量增加而减小的程度。
