建筑抗爆研究中超压的分布特征及确定方法
2020-05-21杨涛春罗尧治
杨涛春,罗尧治
(1.浙江大学 建筑工程学院,杭州 310027;2.济南大学 土木建筑学院,济南 250022)
随着恐怖袭击事件和偶然爆炸事故的不断发生,建筑结构防爆、抗爆研究已成为土木工程领域的热点问题,特别是从“9·11”事件以来,世界多国学者已开展很多相关建筑结构的抗爆研究工作,如爆炸荷载、结构动力响应、破坏模式及简化计算、抗爆分析方法及抗爆加固措施等,得出很多非常有意义的结论,对指导工程结构防爆、抗爆安全有重要参考价值。
在结构抗爆领域的研究中,爆炸荷载的准确与否直接影响抗爆研究结果,因此,如何合理确定作用于结构上的爆炸荷载是首要核心问题。目前,在结构抗爆研究中,已有大量针对爆炸荷载本身的研究,在这些研究成果和实验数据基础上,也形成了相关的规范,以快速指导土木工程抗爆设计,如美国军用防护技术手册TM 5-855-1[1]、TM 5-1300[2]及统一设施标准UFC 3-340-02[3]等,加拿大标准协会CSA S 850-12[4],中国国家标准《爆破安全规程》(GB 6722—2014)[5]及《人民防空地下室设计规范》(GB 50038—2005)[6]等,这些标准或规范把爆炸荷载的理论研究成果与试验数据以公式或图表的形式表达出来,在抗爆设计分析过程中得到广泛应用。在爆炸荷载的计算问题上,不论是规范还是相关计算公式,都给出了相对确定的计算方法,即通过这些方法可得到确定的荷载数值,但不同方法计算得到的荷载数值相差较大,具有较高的离散性,有的甚至相差数十倍,从而导致荷载计算方法选择困难等问题。为此,一些学者从不确定角度出发,通过搜集爆炸荷载数据,统计得到爆炸荷载的概率模型,如Low等[7]对8种常用爆炸荷载计算方法(包括理论公式、经验方法和实验数据)进行统计分析时发现,当比例距离在0.24~40 m/kg1/3范围内时,超压与持时的平均变异系数分别为0.322 7和0.130;而Bogosian等[8]在对300组实验数据和3种计算程序的数据分析时发现,当比例距离在1.2~23.8 m/kg1/3范围内时,超压变异系数为0.24;李忠献等[9-11]通过对77组荷载数据的统计分析,建立了反射超压与持时的平均值、标准值和变异系数与比例距离的拟合关系,并应用于钢梁的可靠度分析,还统计得到具有90%保证率的反射超压和持时计算公式,可用于建筑结构的爆炸荷载取值计算。这些成果对在建筑结构抗爆设计过程中如何确定荷载提供了很好的参考价值。
在前述研究中,通常依据离散随机变量直接计算爆炸荷载的期望或方差,或直接假定爆炸荷载参数变量服从正态分布(连续型),并根据少量试验数据直接以内插值作为不同比例距离对应的试验值。同时,反射超压亦直接通过理论公式基于入射超压求得[12],未考虑反射系数的实际变化情况。基于此,笔者针对理想空中爆炸下爆炸荷载中的超压变量,统计相关理论公式、试验数值和抗爆规范等资料中的爆炸超压计算结果,并根据实际试验得到的反射系数确定相应的反射超压;当某试验比例距离与所需比例距离有差别时,则首先根据已有数据确定此条件下的超压计算公式,再由公式得到所需比例距离下的超压值,从而获得较多的统计数据。根据不同比例距离下的超压数据及直方图,检验确定不同比例距离下的爆炸超压概率分布模型,并得到超压相关指标的极大似然估计量,分析爆炸超压的变异特性,最终给出具有一定保证率的入射超压和反射超压计算方法及置信区间。
1 爆炸超压统计数据
1.1 理论统计数据
目前,很多学者如布罗德(Brode)[13-15]、享利奇(Henrych)[16-17]、Mills[12]、Kinney等[18]和Newmark等[19],对理想空中爆炸条件下的冲击波超压规律及经验公式进行了研究,但各种不同经验公式间还存在着较大差别,特别是离爆心较近时,差别更大,如图1所示。因此,为获得足够有效数据,笔者搜集了18个常用爆炸超压计算公式[1,4-6,12-28],可用来直接计算爆炸超压。
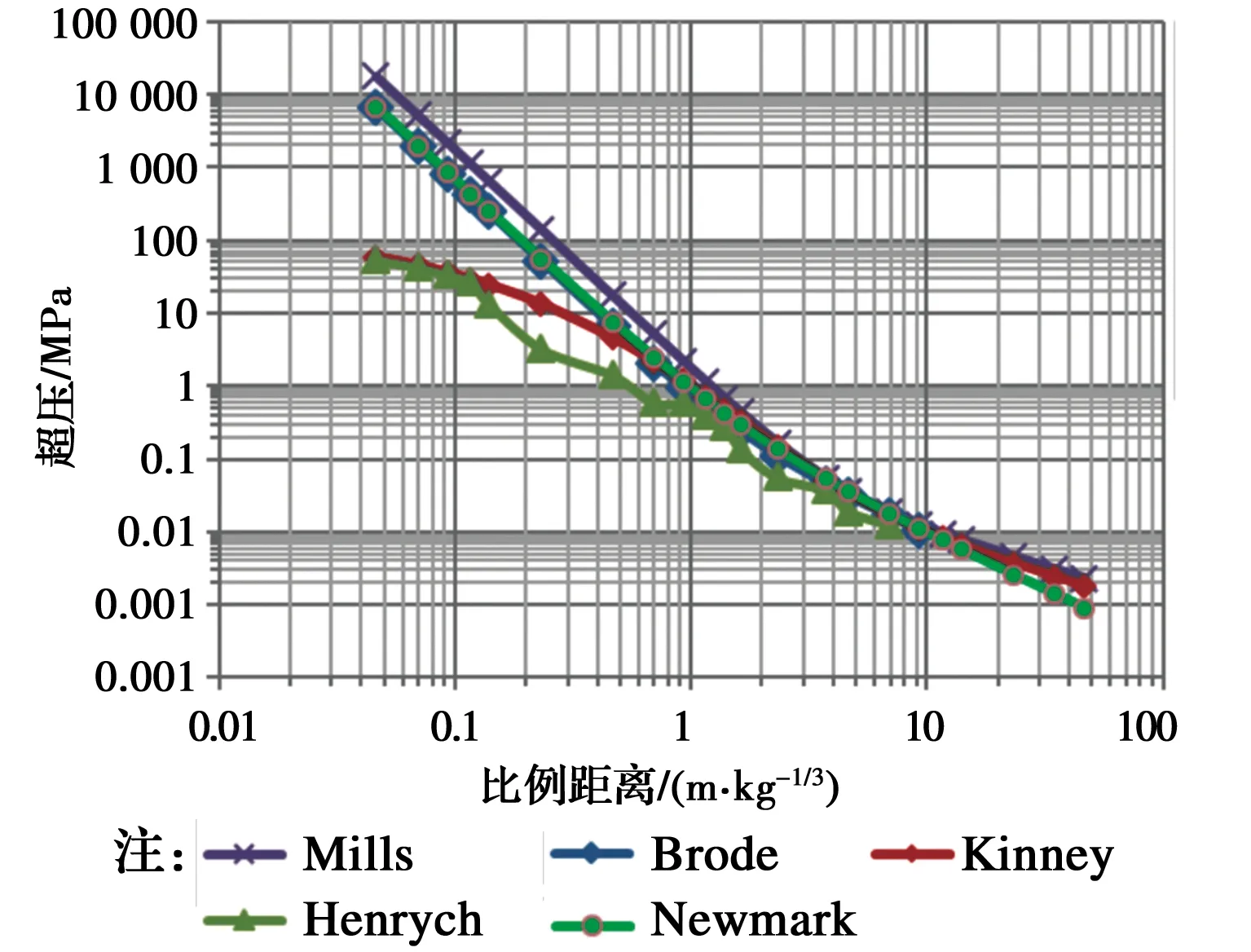
图1 不同冲击波超压公式对比结果Fig.1 Comparison results of different overpressure equations
在搜集的超压计算公式中,反射超压理论或经验计算公式较少,因此,需根据入射超压通过反射系数求得更多反射超压数据,Mills[12]基于理论给出根据入射超压计算反射超压的反射系数表达式,如式(1);而美国军用防护技术手册TM 5-855-1[1]中,基于试验给出反射系数(反射超压与入射超压比值)随入射角的变化关系如图2所示。当仅考虑垂直入射(入射角0°)时,通过式(1)与图2求得的反射系数对比关系如图3所示。由图3可知,在入射超压较小时,理论与实验得到的反射系数基本相等,但当入射超压较大时,实验获得的反射系数最大值13.2,远大于理论计算值8。因此,在根据入射超压和反射系数计算反射超压时,反射系数根据TM 5-855-1[1]实验值确定。为方便获取实验反射系数,对于垂直入射情况,在不同超压下反射系数μ的拟合计算公式如式(2)所示,其回归系数为0.987 1,如图3中虚线,从而得到反射超压与入射超压的关系式(3)。
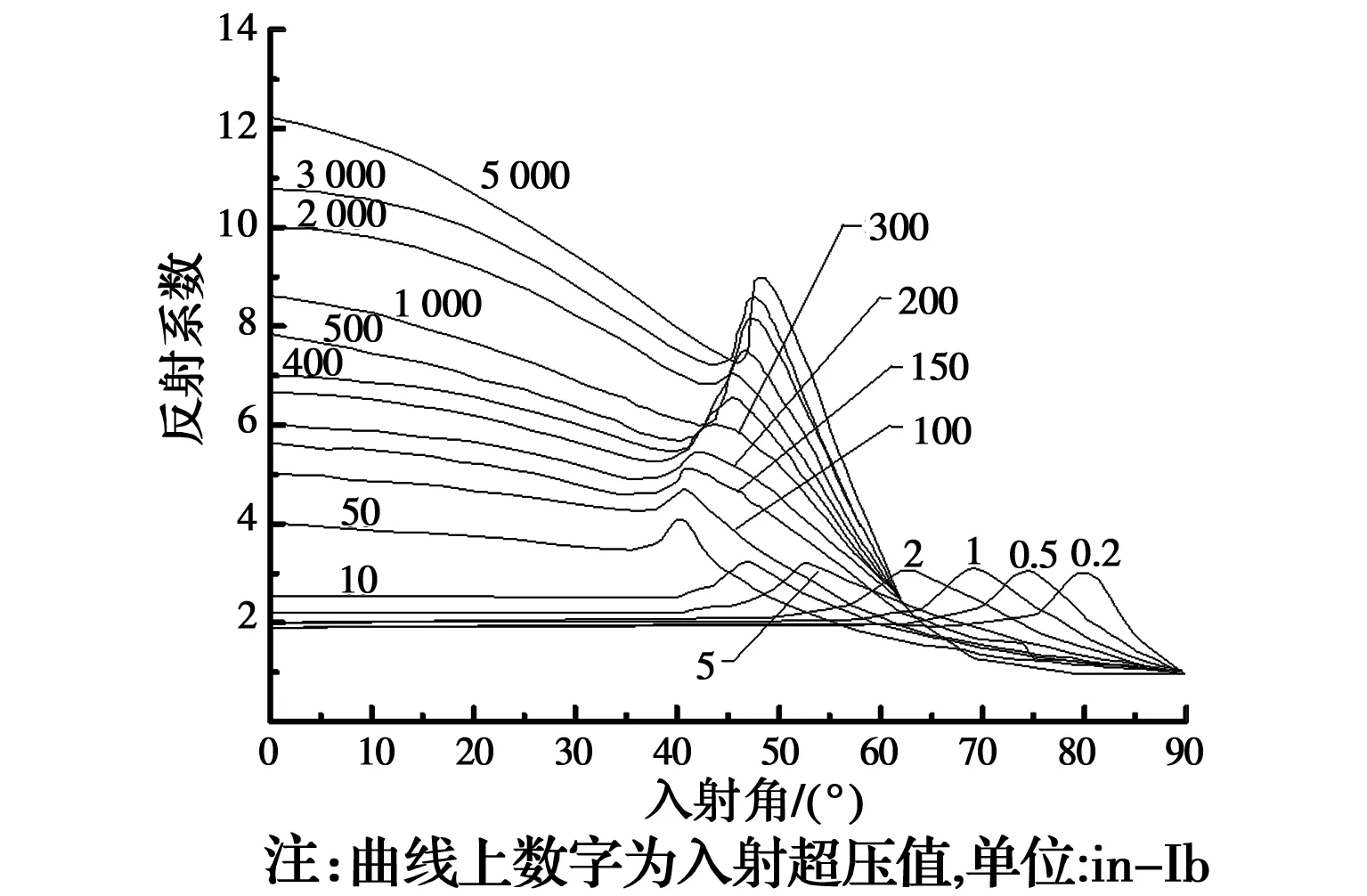
图2 反射系数与入射角关系[1]Fig.2 Relationship between reflection coefficient and incident angle
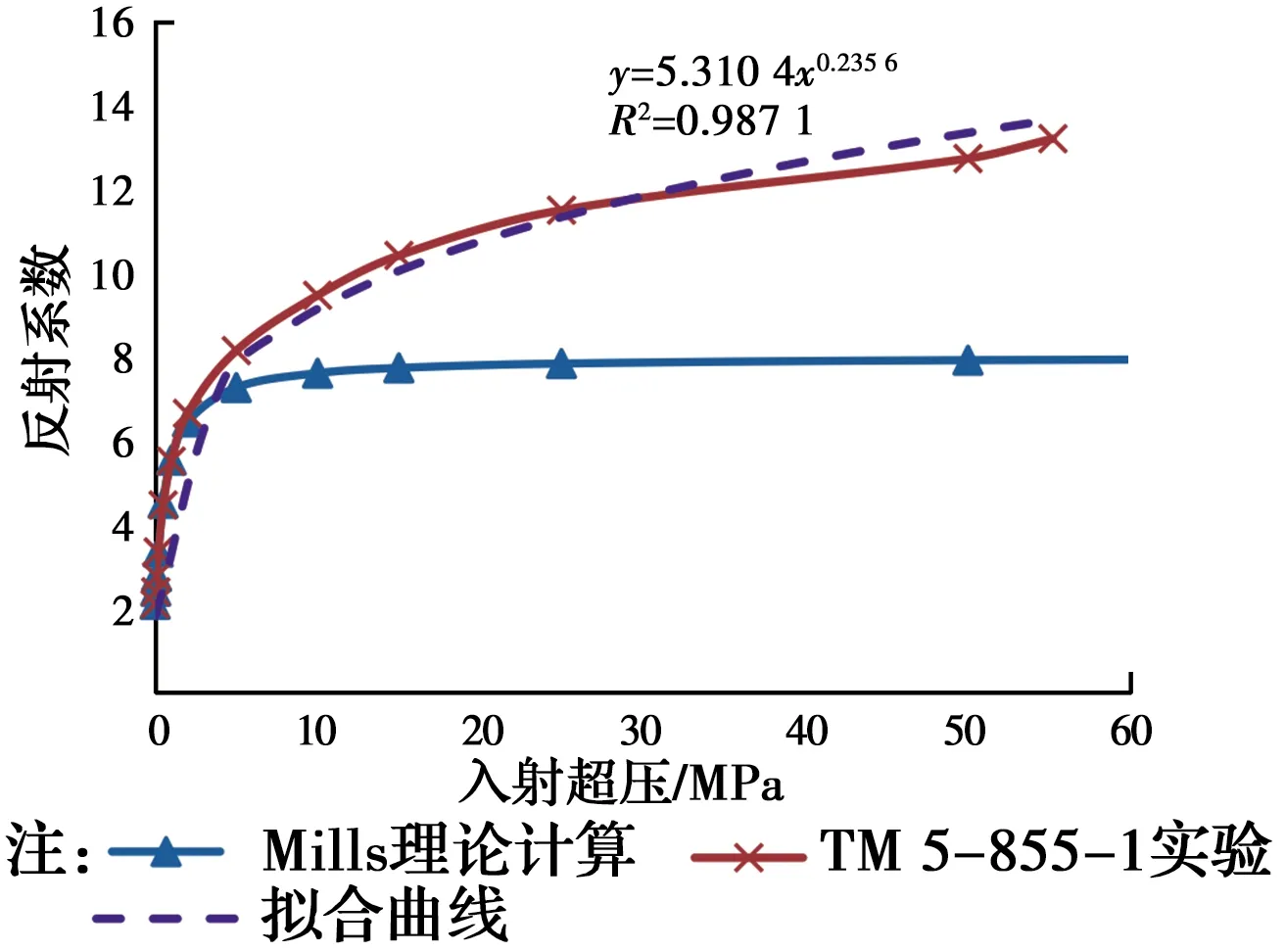
图3 反射系数理论值与实验值对比图Fig.3 Comparison results between theory and test values of reflection coefficients
(1)
μ=5.310 4P00.235 6MPa
(2)
Pr=μP0=5.310 4P01.235 6MPa
(3)
在爆炸荷载计算手段上,已开发出基于试验和理论数据的应用程序,这些程序使用简单方便,已得到广泛应用,因此,在超压数据统计中,也将最常用的Conwep程序计算结果纳入进来。Conwep程序主要基于1959—1964年在加拿大进行的4次5~500 t当量的爆炸试验数据编制,因此,具有相对的真实可靠性,这也是该程序在实际中应用较广的原因。
1.2 实验统计数据
目前,部分学者已开展了一些相关的现场抗爆试验,这些试验数据有助于更加准确地分析爆炸超压的变异程度。通过搜集文献,收集到大量可靠爆炸超压实验数据,共计125组,数据覆盖装药量主要范围为30 g~50 kg,比例距离从0.295 m/kg1/3到55 m/kg1/3,如表1所示。通过对表中数据分析发现,爆炸荷载受环境影响更加敏感,同条件下的多次试验得到的超压值也有一定差异;试验数据中爆炸距离都相对较小,主要集中在5 m以内,这主要受炸药当量较小和试验条件所限,同时也为了降低环境因素的影响;考虑炸药的稳定性和易获取性,部分试验采用ANFO炸药(等效系数0.82)、Emulsion炸药(0.71)、Composite C-4(1.37)、Gelamon VF80(0.8),而非全部采用TNT炸药,这也增加了试验数据的离散性;在部分试验中,装药离地面有一定高度,冲击波与地面的反射等现象也影响到超压大小,且有些试验装药形状非圆形且不规则,特别是当炸药当量较小时,对超压值更有一定影响。因此,在表1的抗爆试验数据中,无法完全避免上述因素的影响,从而使得所收集的爆炸超压本身具有一定的离散性,而这些离散性也是导致爆炸超压不确性的重要影响因素。

表1 爆炸超压试验数据Table 1 Test data of explosion overpressure
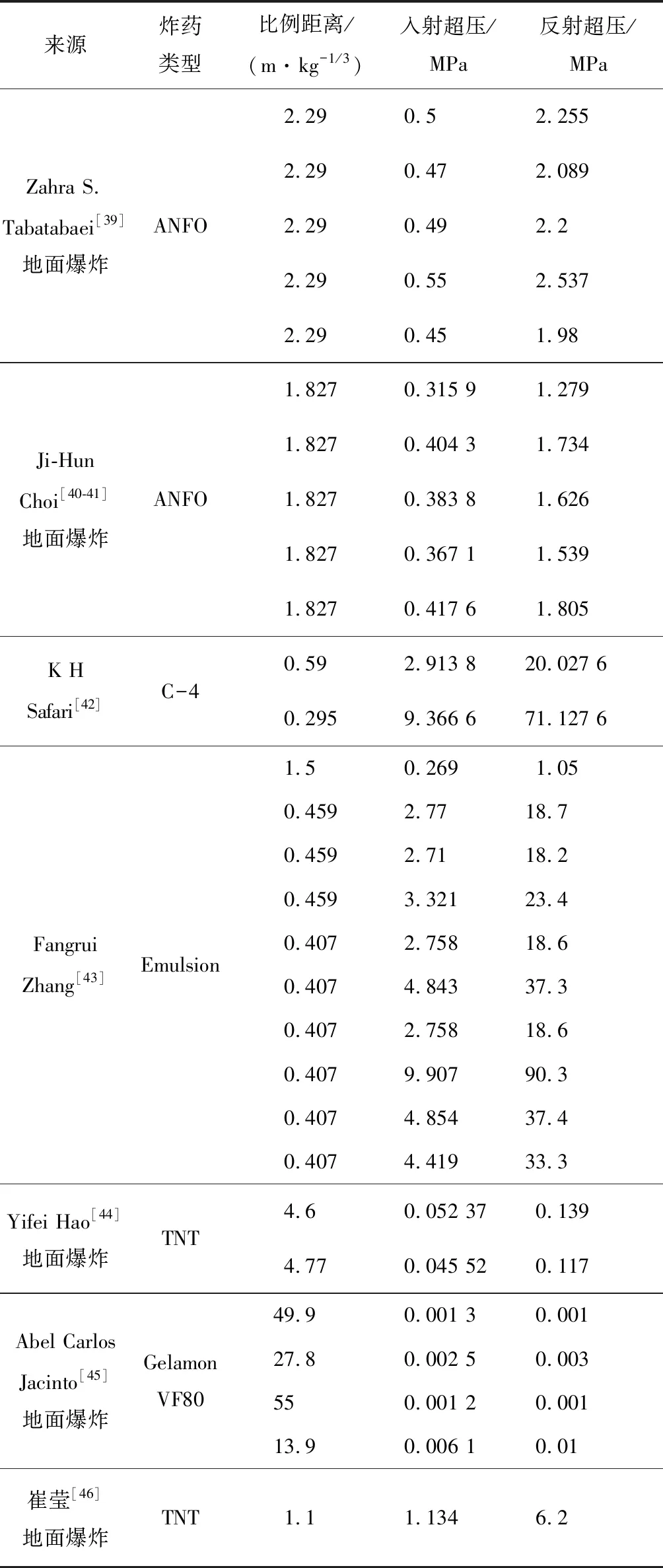
续表1
注:表中只显示部分实验数据,更多参见相关文献。
在搜集的试验数据中,既有垂直入射数据,也有非垂直入射数据,为分析数据的统一和严谨性,仅保留垂直入射的数据,即上述数据共计125组。而在这125组试验数据中,有的仅有入射超压,有的仅有反射超压,入射超压与反射超压同时存在的只有11组,对于同批试验,有22组数据存在较大差异,在分析中未考虑,因此,实际使用的试验统计数据有103组。
分析爆炸超压计算公式发现,入射超压的计算公式主要有两种形式,如式(4)、式(5)所示,在每个公式中,均存在3个待定系数。其中,式(4)通过爆炸力学理论求得,并通过试验确定相关系数,此方法在已有入射超压的计算公式中得到更多应用,式(5)主要通过试验数据拟合而得,在入射超压的计算公式中也有一定应用。对于统计的仅有入射超压或反射超压的试验数据,通过反射系数式(2)和入射超压计算公式可得到该组试验条件下的相关入射超压公式和反射超压相关数据,为分析得到爆炸超压的概率分布特征提供统计样本。
(4)
P0=d·Ze+f
(5)
式中:Z为比例距离。
2 超压分布特征
基于统计的爆炸超压数据,对不同比例距离下的离散超压值进行分析,画出对应不同比例距离的超压分布直方图,结合超压直方图分布特征,并通过K-S检验和Lilliefors检验分别开展不同比例距离下的超压概率分布拟合优度检验。结果表明,当比例距离小于0.5 m/kg1/3时,入射超压和反射超压分布均服从指数分布,当比例距离大于0.5 m/kg1/3时,超压分布均服从正态分布。在确定概率分布模型基础上,计算得到不同比例距离条件下的超压均值和标准差的极大似然估计值,同时,得到超压均值在95%保证率条件下的置信区间,如表2、表3所示,从而得到不同比例距离下的超压分布概率密度曲线,如图4、图5所示(指数分布和正态分布各两组)。从表2、表3中可以看出,比例距离较小时,标准差最大,超压分布越分散。
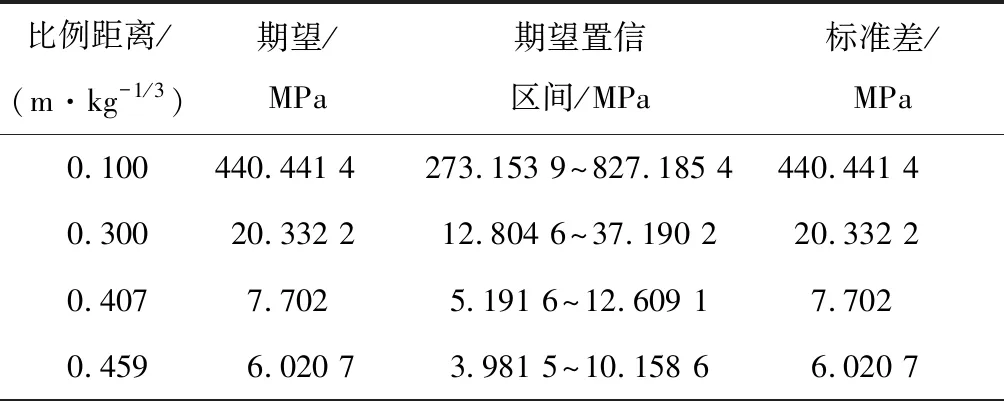
表2 入射超压的期望与标准差的极大似然估计值Table 2 ML estimate of expectation and standard deviation for incident overpressure
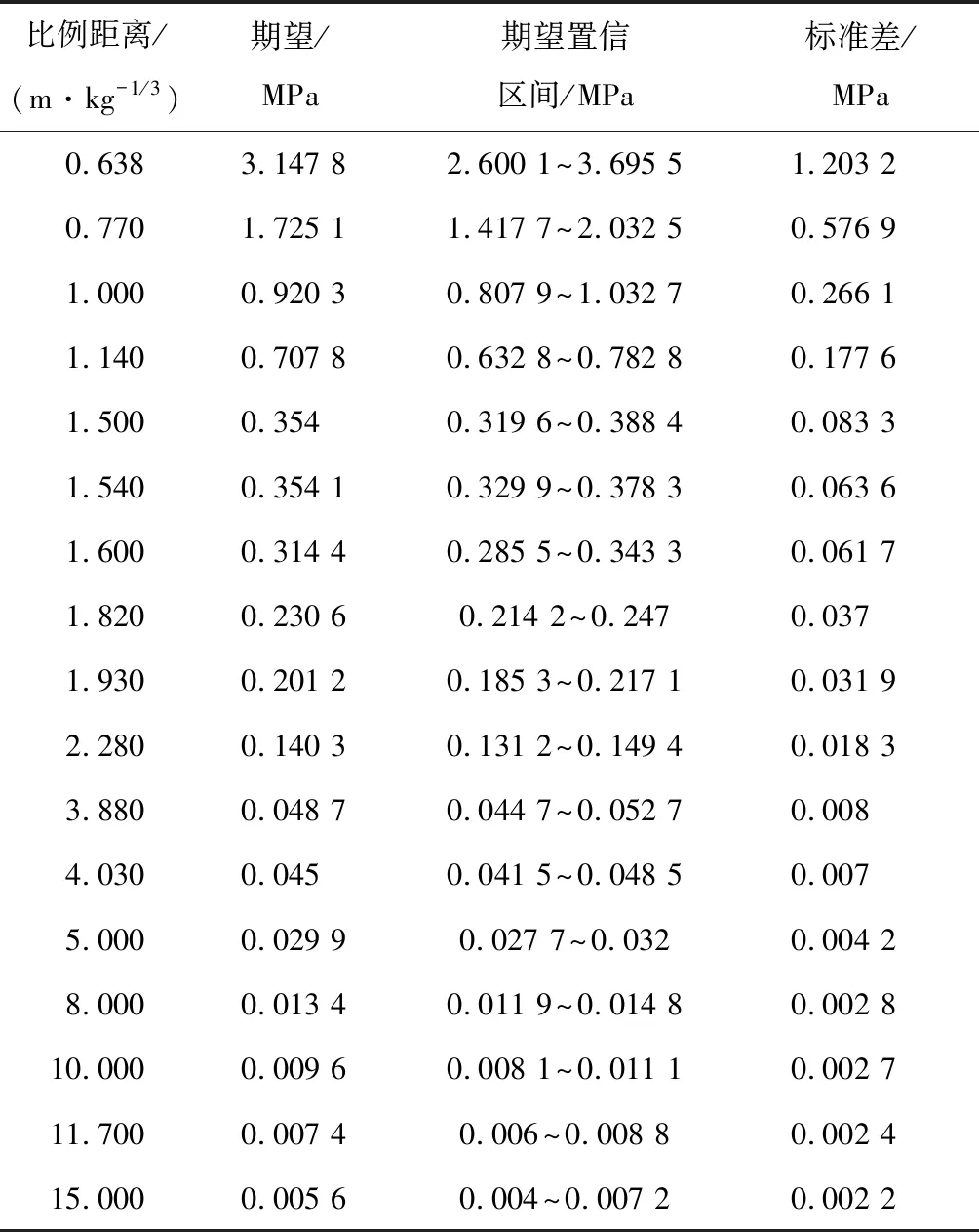
续表2
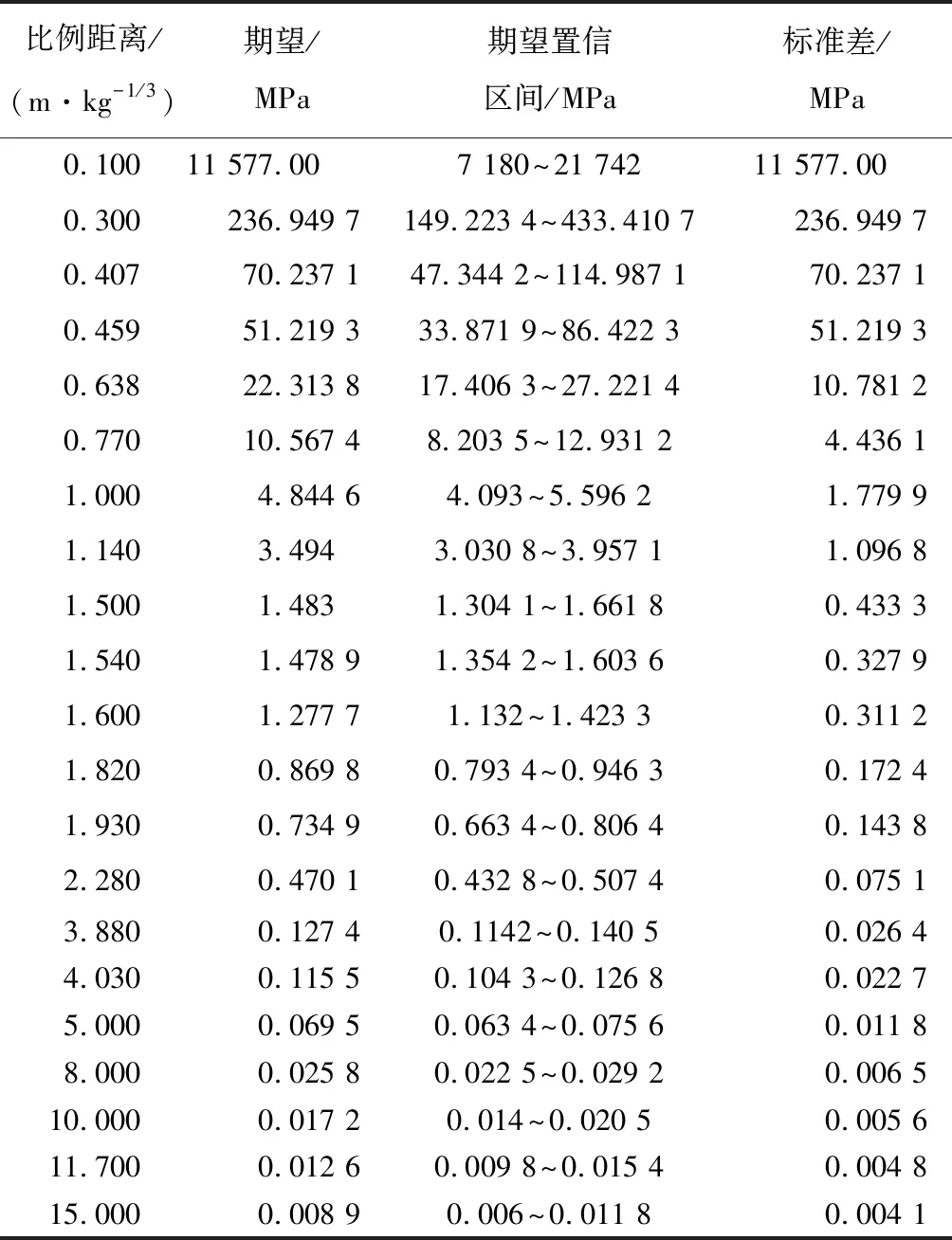
表3 反射超压的期望与标准差的极大似然估计值Table 3 ML estimate of expectation and standard deviation for reflection overpressure
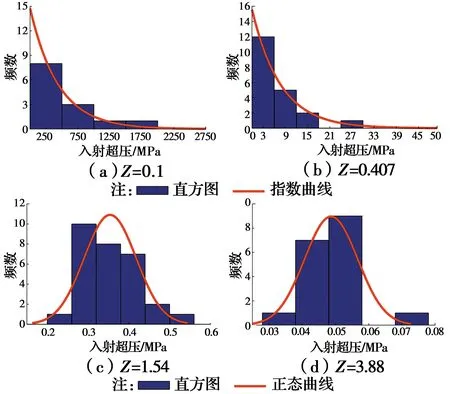
图4 不同比例距离下的入超压分布直方图与概率密度曲线Fig.4 Histogram and probability density curve of incident overpressure under different scaled distance
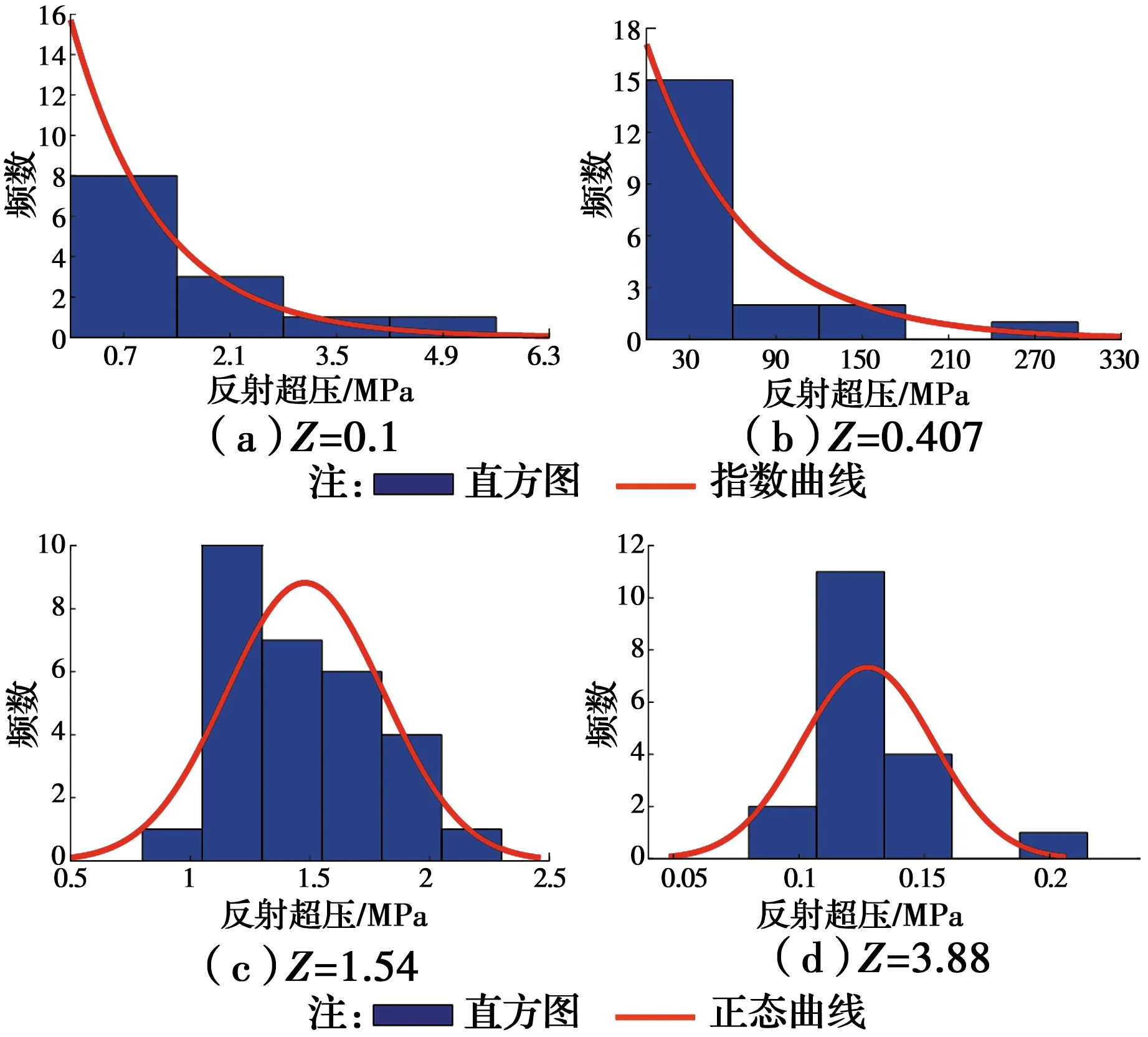
图5 不同比例距离下的反射超压分布直方图与概率密度曲线Fig.5 Histogram and probability density curve of reflection overpressure under different scaled distance
为对比不同比例距离条件下入射超压与反射超压的分散程度,通过表2、表3中超压期望和标准差的极大似然估计值得到超压分布的变异系数,如图6所示。从图6可以看出,比例距离小于0.5 m/kg1/3时,
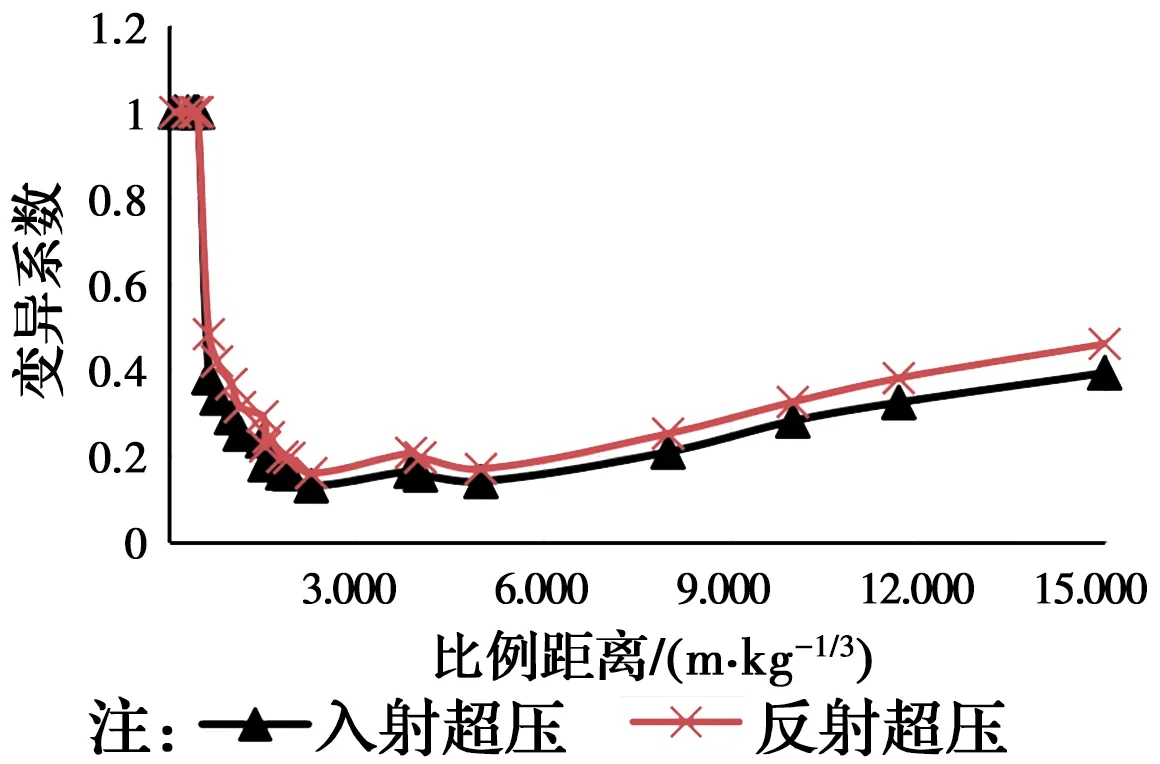
图6 不同比例距离下超压分布变异系数Fig.6 Variation coefficient of overpressure under different scaled distance
超压变异系数达到最大,为指数分布的常值1;当比例距离约在1.5~6 m/kg1/3之间时,得益于较多的试验数据,变异系数较小,在0.13~0.2之间,且反射超压的变异系数较入射超压略大。
3 爆炸超压公式确定
根据表2、表3中超压期望的极大似然估计值,可得到入射超压和反射超压95%置信区间上、下限随比例距离的变化关系,分别如图7、图8所示,因不同比例距离的超压值相差较大,故将比例距离分3段分别绘制,从图中也可看出超压分散程度随比例距离的变化趋势,比例距离越小,超压分布越分散。取比例距离和超压值的自然对数,再通过最小二乘法对自然对数超压进行多项式拟合,如图9、图10所示,入射超压和反射超压拟合曲线的回归系数均大于0.99,最终得到入射超压的计算公式为
lnP0=0.158 3ln2Z-2.342lnZ-0.097 7
(6)
入射超压95%置信区间上、下限的计算公式为
lnP0=0.214 9ln2Z-2.486 7lnZ+0.071 1(上限)
(7)

图7 入射超压及其95%置信区间随比例距离变化关系图Fig.7 Change relation of incident overpressure, 95% confidence interval with scaled
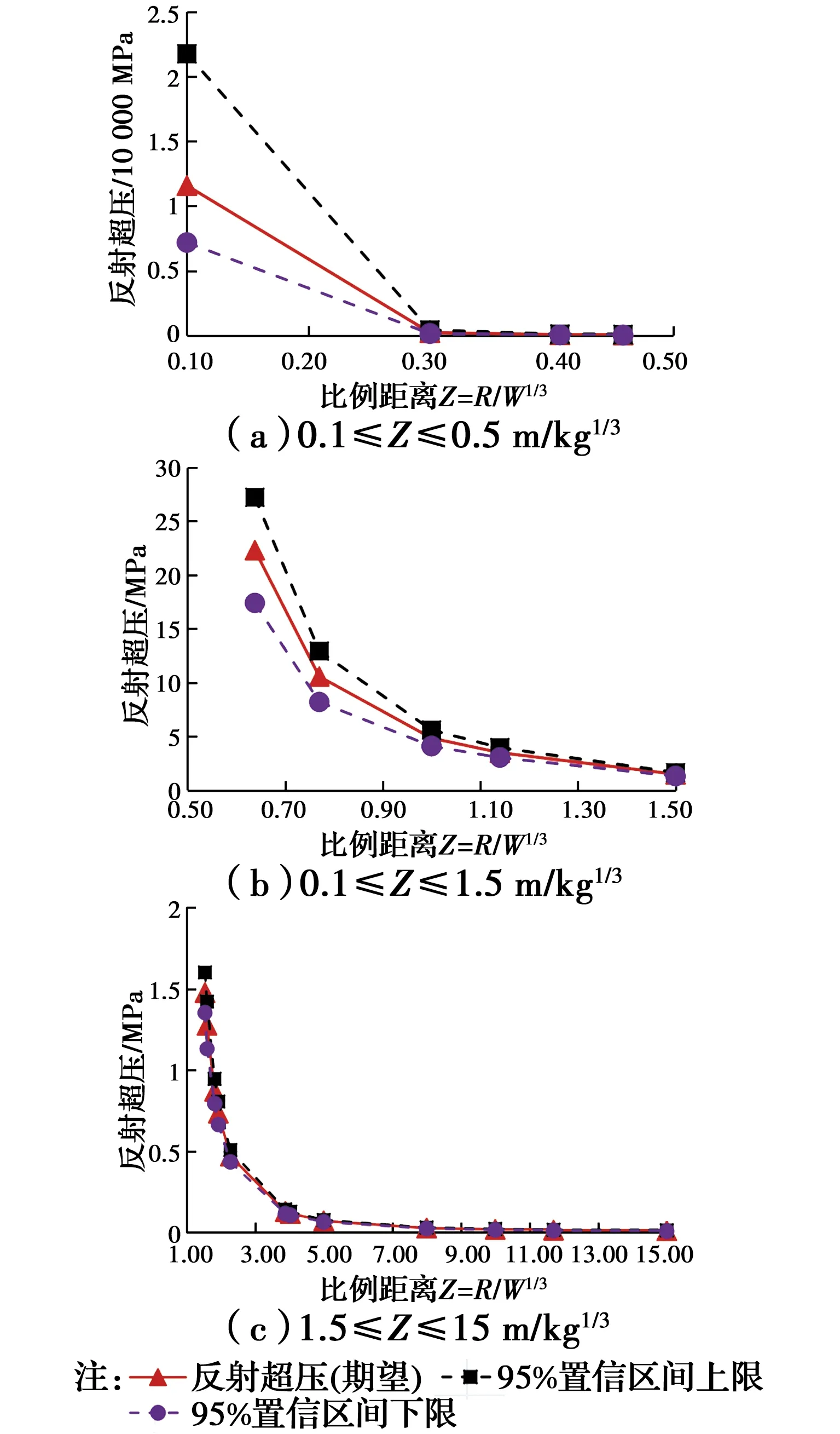
图8 反射超压及其95%置信区间随比例距离变化关系图Fig.8 Change relation of reflection overpressure, 95% confidence interval with scaled

图 9 入射超压及其95%置信区间与比例距离关系拟合曲线Fig.9 Fitting curve of incident overpressure, 95% confidence interval with scaled
lnP0=0.111 1ln2Z-2.242 8lnZ-0.250 6(下限)
(8)
同理,可得到反射超压的计算公式为
lnPr=0.208 7ln2Z-2.926 3lnZ+1.564 7
(9)
反射超压95%置信区间上、下限的计算公式为
lnPr=0.264 3ln2Z-3.065 2lnZ+1.751 2(上限)
(10)
lnPr=0.162ln2Z-2.833 9lnZ+1.389 8(下限)
(11)
其中,比例距离Z在0.1~15 m/kg1/3范围内。
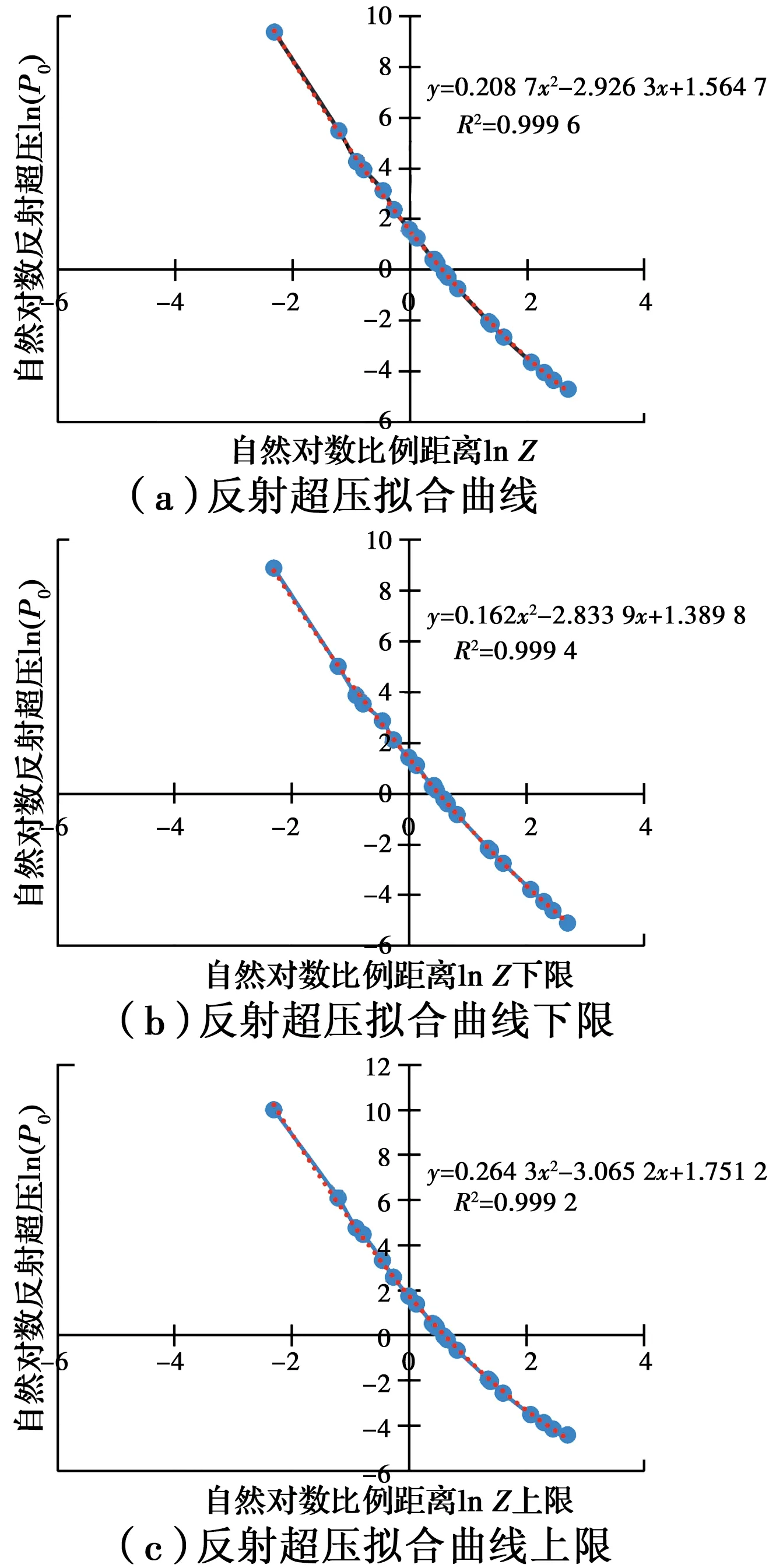
图10 反射超压及其95%置信区间与比例距离关系拟合曲线Fig.10 Fitting curve of reflection overpressure, 95% confidence interval with scaled distance
4 结论
通过搜集文献获取大量爆炸超压的试验与理论数据,并从不确定性角度出发,研究了爆炸超压的概率分布特征,主要得到以下结论:
1)爆炸超压试验数据受炸药类型、当量、形状及试验环境等因素影响明显,超压分布具有较高的离散性,且试验数据多以小当量炸药为主,比例距离多集中于0.4~2.0 m/kg1/3之间。
2)基于试验数据,针对垂直入射情况拟合给出反射系数公式,并得到根据入射超压获取反射超压的计算公式。
3)比例距离小于0.5 m/kg1/3时,爆炸超压概率密度服从指数分布;比例距离大于0.5 m/kg1/3时,爆炸超压概率密度服从正态分布。
4)比例距离小于0.5 m/kg1/3时,爆炸超压变异系数达最大值1;比例距离约在1.5~6 m/kg1/3间时,变异系数较小,在0.13~0.2之间;反射超压变异系数较入射超压略大。
5)根据不同比例距离下爆炸超压分布期望数据,拟合得到爆炸超压的计算公式与具有95%保证率条件下的超压分布范围计算公式。
