疲劳荷载作用下植筋锚固粘结的滑移性能
2020-05-21阎西康梁琳霄梁琛
阎西康,梁琳霄,梁琛
(1. 河北工业大学 土木与交通学院,天津 300401;2.中建地产(天津)有限公司,天津 300450)
随着承受疲劳荷载的结构如吊车梁、桥梁等的维修、改造工程日益增多,植筋技术在这方面的应用研究愈加广泛[1-2]。植入钢筋的粘结滑移性能是保证植筋结构稳定安全的关键因素[3-5],部分学者对静载作用下植筋与混凝土界面、植筋与植筋胶界面的结合性能做了一定研究,主要集中在植筋直径、混凝土材料强度、保护层厚度、施工质量等因素对植筋粘结强度的影响[6-7]。Wang等[8-9]对直径36~150 mm的螺杆锚固破坏形式进行分析,给出了大直径植筋系统拉拔承载力计算公式。植筋拉拔试件在高温环境中的力学性能研究表明,温度对植筋拉拔滑移的影响较大[10]。Mahrenholtz等[11]给出了不同锚固设计方法对植筋拉拔承载力的影响。
疲劳荷载作用下植筋构件的力学性能与静载作用下区别很大,结构设计时需进行疲劳计算[12],其结果是否可靠,部分取决于材料动力本构模型的建立。文献[13]进行了植筋深度在10d~15d(d为植筋直径)的植筋拟动力拉拔试验,发现动力加载后试件延性损失较多。但承受疲劳荷载的构件植入深度一般在20d以上,相较于实际应用,植筋结构在疲劳荷载作用下的锚固机理研究略显滞后,植筋与植筋胶、植筋胶与混凝土的动力粘结性能尚有待深入研究。
笔者对疲劳荷载作用下植筋构件的胶筋界面粘结性能进行分析,设计了10组拉拔试验,研究受拉植筋锚固问题,获得了疲劳荷载作用下植筋试件的荷载-滑移关系和植入钢筋与植筋胶间的粘结力变化规律。
1 试验概况
试验设计2个C30强度、尺寸为1 800 mm×1 000 mm×700 mm的混凝土块体试件。在每个混凝土试件顶面,按照《混凝土结构加固设计规范》(GB 50367—2013)[14]中植筋钻孔和间距的要求,植入10根不同直径、不同植筋深度的HRB400级钢筋,一个试件上的10根植筋用于静力拉拔试验,另一个试件上的植筋用于疲劳加载试验。加载方式如图1所示。

图1 加载方式示意图Fig.1 Loading method diagram
混凝土浇筑时预留3块150 mm×150 mm×150 mm的标准立方体试块,以测定立方体抗压强度。表1、表2给出了试验所用的混凝土和钢筋的基本参数。植筋表面均匀布置5个应变片,测量植筋应变,图2为不同锚固深度的植筋应变片布置。为保证应变片粘贴牢固,在钢筋表面预定位置打磨出面积稍大于应变片的平面后,用丙酮清洁钢筋表面。使用502粘贴剂将应变片贴在钢筋表面后,用纱布蘸取环氧树脂包裹应变片,养护至环氧树脂完全硬化,防止其在植筋施工和后期加载过程中损坏。混凝土试件浇筑并养护28 d后,按照文献[14]要求的钻孔直径,在混凝土试件顶面利用水钻垂直钻孔,然后,将试件倾斜,向孔内泵送压缩空气进行除尘干燥处理,保证清孔彻底。植筋胶采用德国慧鱼FISEM390S,孔内灌注FISEM390S后将钢筋缓慢旋转植入,钢筋完全达到预定锚固深度时,孔口有少量植筋胶溢出,确保灌浆饱满。植入钢筋后,养护24 h,利用电液伺服动力系统进行拉拔。在植筋接近混凝土试件上表面的位置固定夹片来测量植筋滑移(见图3)。通过DH5922N通用型动态信号测试分析系统以每秒50个数据的频率采集应变、植筋滑移数据,采集设备如图4所示。

表1 混凝土材料配合比及强度实测值Table 1 Mix proportion and actual strength of concrete
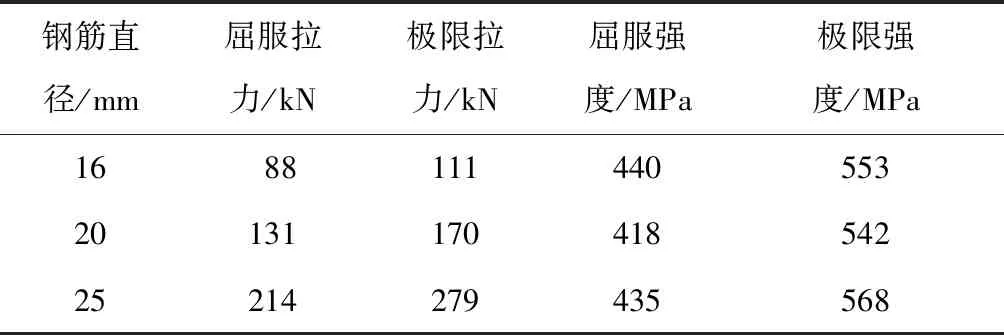
表2 钢筋强度实测值Table 2 Actual strength of rebar
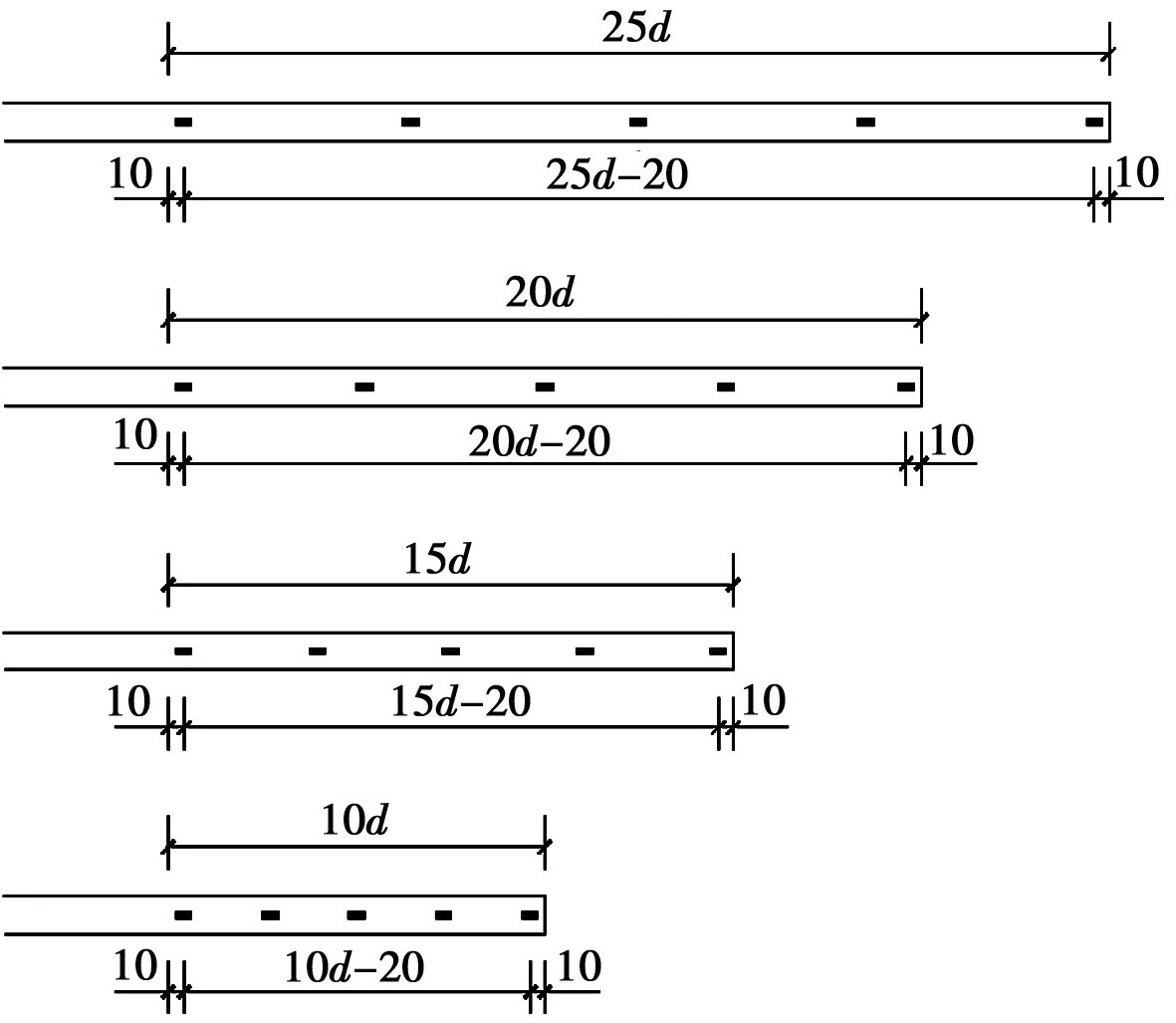
图2 植筋表面应变片布置Fig.2 Arrangement of strain gauges

图3 植筋滑移测量Fig.3 Slip measuring device

图4 数据采集设备Fig.4 Data acquisition device
试件编号J1~J10施加静力拉拔荷载。编号P1~P10施加频率为6 Hz、加载上限为0.45Pu、加载下限为0.2Pu(Pu为静载试验测出的极限荷载)的疲劳拉拔荷载,在循环次数达到1、10、50、100、150万次时暂停,进行一次静力分级加载,加载至疲劳上限再卸载,每级荷载为10 kN。经过200万次疲劳加载后,试件未破坏,采用静力加载至破坏。疲劳加载使用结构抗震拟动力试验系统jaw-1000/4实现并自动记录荷载时程变化。各试件参数详见表3。
2 试验结果与分析
2.1 破坏形态
20个试件的破坏形态:J4、J7、J10、P4、P7和P10共6个试件均被拔出,其余试件钢筋在混凝土表面附近拉断。
J4、P4植筋被拔出后,植筋胶体较完整地附着在植筋表面,距加载端一定长度范围内混凝土呈锥体破坏,剩余部分胶体表面光滑,符合锥体-粘结混合破坏特征,如图5所示(锥体未能完整保留,试验过程中锥体如图6所示)。J4混凝土锥体长度为113 mm,P4混凝土锥体长度为91 mm。J7、J10、P7、P10为胶筋粘结破坏,见图7。J7、P7靠近植筋自由端152、177 mm范围内的胶体破坏,J10、P10靠近植筋自由端124、139 mm范围内的胶体破坏。疲劳试件胶体破坏范围大于静力破坏试件。从图7可看到,钢筋横肋间残留胶体,竖肋两边钢筋表面没有胶体粘附,最终破坏形式为胶筋间粘结破坏。被拉断的试件最终破坏见图8。试件的破坏荷载见表3。

表3 平均粘结应力及残余滑移Table 3 Average bond stress and residual slip

续表2

图5 锥体-粘结混合破坏
Fig.5Compound failure

图6 锥体-粘结混合破坏过程Fig.6Failure process of compound failure

图7 胶筋界面粘结破坏
Fig.7 Bond failure of interface

图8 拉断破坏Fig.8 Rebar tensile failure between anchor bar and chemical adhesive
2.2 荷载-滑移关系
试验得到不同试件的荷载-位移关系,对比了经历疲劳作用后静载破坏的试件与未经过疲劳加载的试件破坏过程的区别。图9中疲劳试件的荷载-位移曲线为200万次循环加载后静力破坏时的数据。从图9可见,经疲劳荷载作用后,与静载时相比,试件的极限荷载分别下降17.58%、18.98%、22.59%、20.10%、12.58%、18.56%、15.32%、5.79%、14.41%、17.39%。试件的荷载滑移图像首次出现突变时即植筋出现初滑移,经疲劳加载的植筋试件初滑移荷载下降13.73%、19.51%、21.11%、17.49%、20.69%、11.11%、14.63%、8.89%、7.14%、17.65%。对于拉断破坏的试件,极限荷载取决于植入钢筋的极限强度[11],植筋直径相同时,植筋深度增加,极限荷载基本不变,但经疲劳加载后极限荷载下降5.79%~22.59%。对于植筋拔出破坏的试件,锥体粘结混合破坏和胶筋粘结破坏的极限荷载远低于拉断破坏的试件:静载破坏试件,植筋拔出与植筋拉断的极限荷载相差23.72%~25.78%;疲劳加载后破坏的试件两者相差24.46%~33.33%。

图9 荷载-滑移关系Fig.9 Load-slip curves
20个试件的荷载-滑移关系可分为两组:植筋被拉断的J1、J2、J3、J5、J6、J8、J9和P1、P2、P3、P5、P6、P8、P9的荷载-滑移曲线与普通钢筋受拉破坏试验的情况类似,可看成线性增长段、屈服段及下降段。植筋拔出的J4、J7、J10和P4、P7、P10试件曲线分为上升和下降两个阶段。加载开始,滑移和荷载呈线性关系,为弹性阶段,植筋粘结弹性极限通常为0.75Pu;在弹性比例极限后,曲线进入非线性阶段,荷载增长缓慢,滑移增长加快,植筋拉断的试件此阶段持续较长,钢筋屈服,植筋拔出的试件此阶段不明显,植筋深度较小的试件在曲线上升后直接进入下降段;荷载到达极限后,曲线进入下降段,直至钢筋拉断或拔出,植筋拔出的试件下降段明显较长,在界面破坏后,摩擦力起主要作用,维持较小荷载下试件被缓慢拔出。
J10试件植筋深度和钢筋直径最小,由于应变片布置较密,导致植筋表面积损失约12.4%,与已有文献[15]中单调受拉试验结果破坏特征一致,但极限荷载下降9.61%。J7、J4试件植筋表面积损失约7.9%和6.3%,极限荷载也有所降低。相应地,P10、P7、P4的荷载结果也应考虑约10%~5%的折减。其他试件的植筋表面积损失比例很低,可忽略这种不利影响。
2.3 疲劳荷载作用下植筋粘结机理
2.3.1 植筋粘结应力 由表3可见,植筋直径一致的情况下,随植筋深度增加,破坏时粘结应力反而下降。植筋深度增长,外力会由全部的锚固深度范围内植筋均匀分担,相比之下,单位深度的粘结应力较植筋深度小的试件小,有利于避免局部破坏。
植筋胶筋粘结应力由试验实测的应变数据采用有限差分法处理,由式(1)计算得出。
(1)
式中:Es为钢筋弹性模量,N/mm2;As为钢筋面积,mm2;D为钢筋直径,mm;Δxj,j+1为两应变片测点间距,mm;εj、εj+1分别为第j、j+1点的钢筋应变值。
根据疲劳试件的胶筋粘结应力与植筋深度的关系,分析粘结应力分布的变化规律,图10给出了钢筋被拔出的J4、J7、J10、P4、P7、P10的试验结果。疲劳试件的结果采用200万次循环加载后静力破坏过程中的粘结应力实测值。静载与疲劳试件粘结应力规律一致,植筋粘结应力分布的特点:加载初期应力峰值均靠近加载端出现,且峰值与平均值差别较大,在峰值应力处出现混凝土锥体破坏;继续加载,应力峰值增加为两个,且较大值出现在植筋自由端;植筋深度相同(10d),直径越大,加载后期应力峰值与平均粘结应力越接近,植筋粘结应力分布越匀称。
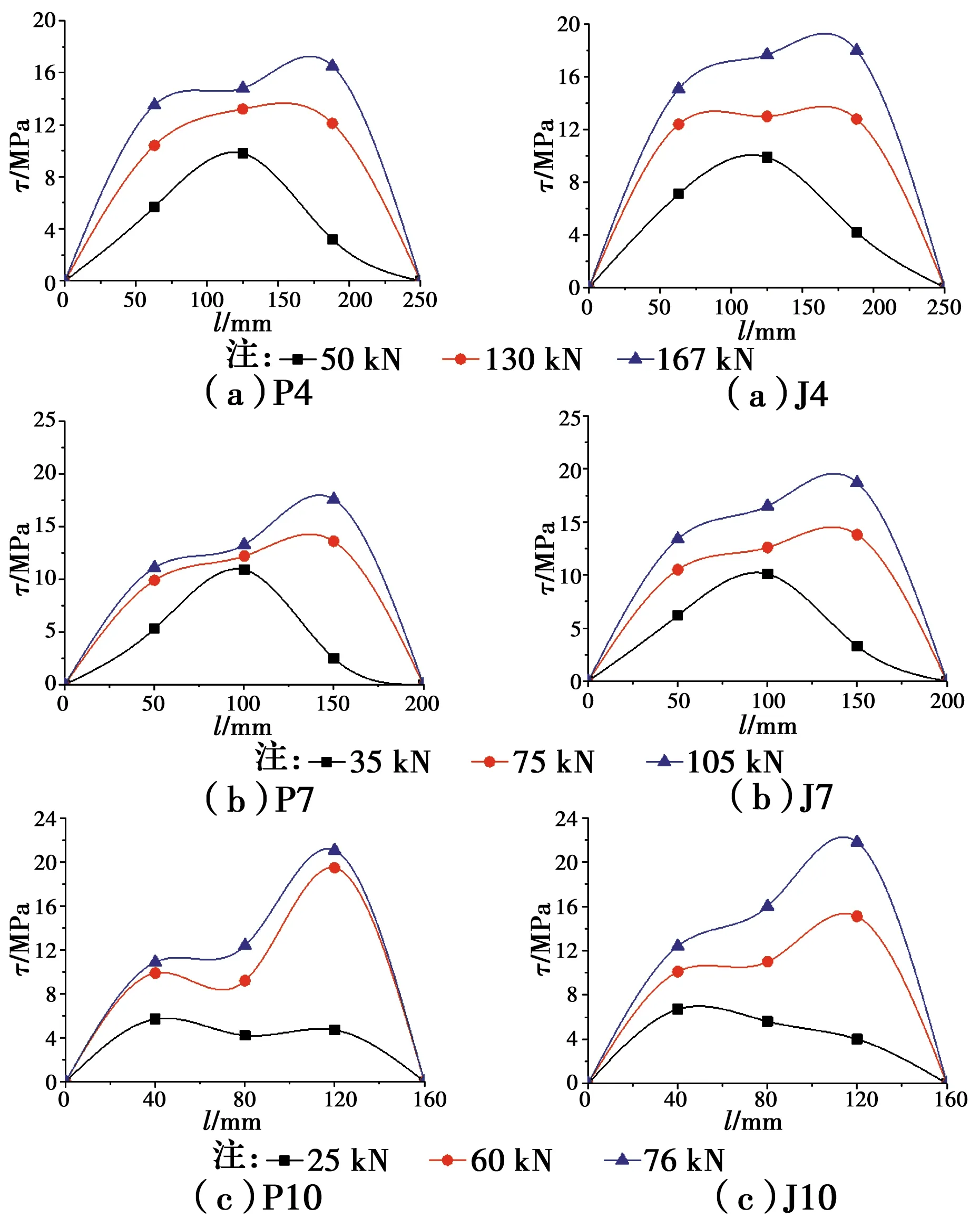
图10 粘结应力-植筋深度关系Fig.10 Relationship between bond stress and depth of planting
由于植筋表面布置应变片导致粘结性能下降,相较于植筋表面未受损伤的静力拉拔试验结果[15],J10粘结应力下降7.85%。相应地,P10、P7、P4的粘结应力结果也应考虑约8%~4%的折减。
2.3.2 疲劳荷载对粘结应力的影响 与静力加载试验结果相比,疲劳加载使植筋拉拔试件在同等荷载级数下的平均粘结应力降低。图11给出了不同破坏形态下的3种试件在疲劳加载过程中粘结应力的变化情况:P4为锥体粘结混合破坏,P1、P2、P3、P5、P6、P8、P9为拉断破坏,P7、P10为胶筋粘结破坏。图中横坐标N为荷载循环次数,纵坐标τ0/τ是荷载相同(取循环加载上限)时静载与循环加载试验得到的平均粘结应力的比值。例如:J10在40 kN时测得的粘结应力为4.38 MPa,P10试件在循环次数达到1、10、50、100、150、200万次时暂停进行静力加载至疲劳上限40 kN时测得的平均粘结应力为4.29、4.19、3.84、3.92、3.57、3.6,两者之比1.00、1.02、1.05、1.14、1.12、1.23、1.22即图中P10纵坐标的读数。
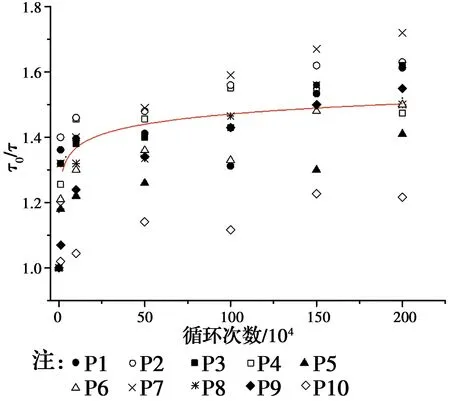
图11 疲劳粘结应力随循环加载次数变化规律Fig.11 Relationship between bond stress and the number of cyclic loading
不同试件的粘结应力退化情况基本相同,都是在前50万次迅速下降,之后下降趋于平缓。疲劳上限是破坏荷载的0.45倍,两者差距较大,在低应力状态下,最终的破坏形态不同对粘结应力降低影响不大。分析所有疲劳试件的疲劳粘结应力随循环加载次数变化规律可知,循环加载对植筋粘结应力的影响基本呈对数关系,如式(2)所示。表4给出了全部疲劳试件在200万次循环加载达到疲劳上限时测得的平均粘结应力与式(2)计算得出的理论值的对比。式(2)的计算结果与实测数据两者相差最大达23.46%。
τ=τ0/(1.264+0.0451nN)
(2)
式中:τ为循环加载得到的植筋平均粘结应力,MPa;τ0为静力加载得到的植筋平均粘结应力,MPa;τ0为循环加载次数,万。
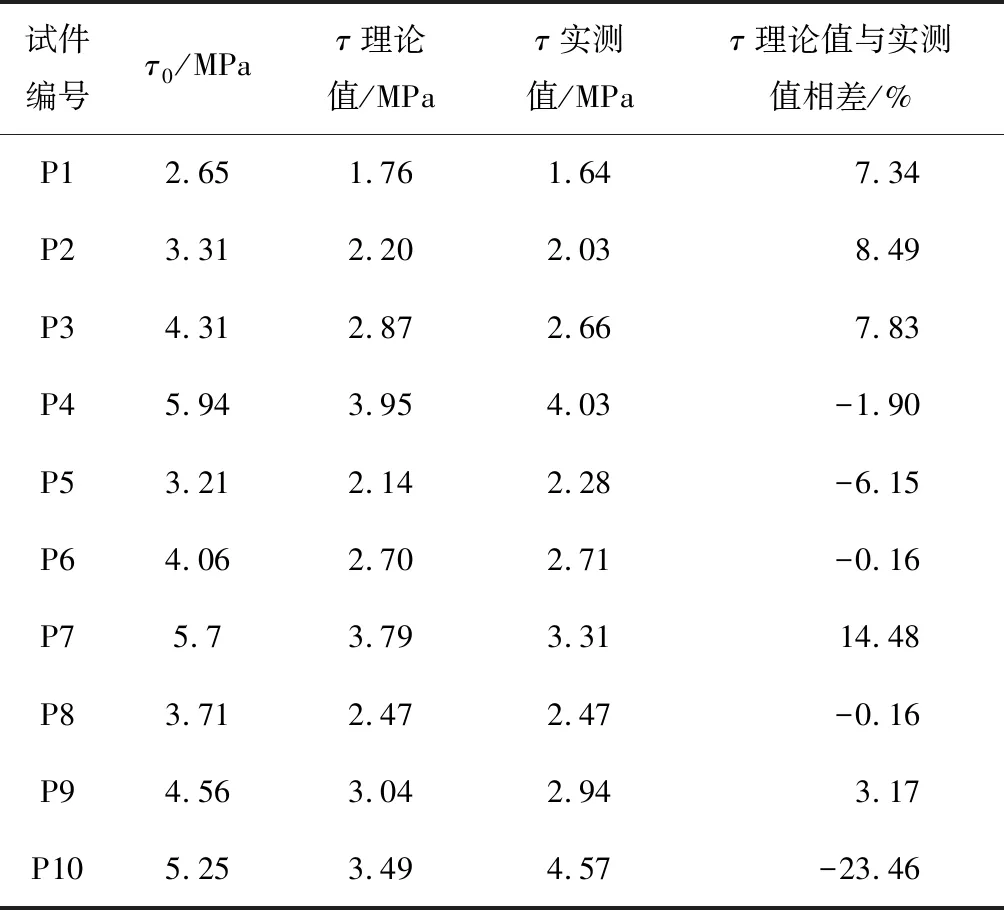
表4 平均粘结应力实测值与理论值对比Table 4 Comparison between measured value of average bond stress and theoretical value
2.3.3 胶筋界面粘结滑移 由植筋系统进行受力分析可知[9],植筋深度、植筋钻孔直径一定时,与各材料间的粘结应力是决定破坏形态的关键因素。J7、J10、P7、P10拔出后,加载端约1/5长度破坏时混凝土呈椎体,剩余4/5长度为胶筋破坏,与上文得出的τs沿植筋深度传递、随荷载增加最大剪应力逐渐向植筋末端传递的结果一致。试件发生初滑移是由于靠近加载端的植筋段胶混界面滑移所致,此时胶筋界面的粘结应力还没有得到充分发挥。总结植筋试件的破坏特征可知,植筋达到一定深度时,胶筋界面的粘结应力是防止试件破坏要考虑的主要因素,且τs、τc之间存在一定比例关系,故只对胶筋界面粘结应力τs进行分析,即下文的τ。
P4、P7、P10最终因胶筋界面粘结失效而被拔出,但其他疲劳试件均为植筋拉断破坏。试件被拉断说明胶筋界面粘结可靠,故分析胶筋界面粘结滑移时以P4、P7、P10为分析对象。由于τ沿植筋长度的分布并不规则,建立疲劳荷载作用下粘结滑移本构关系时使用平均粘结应力,则粘结应力-滑移曲线规律同荷载-滑移关系由曲线分布可确定3个特征点:初滑移粘结应力τ0、初滑移值S0、对应初滑移荷载P0,极限粘结应力τu、极限滑移值Su、对应极限荷载Pu,残余粘结应力τr、残余滑移值Sr、对应破坏荷载Pr。
由文献[16]可知,静力作用下植筋拉拔发生界面破坏的极限粘结强度τus为
(3)
式中:fcu为混凝土立方体抗压强度,MPa。
考虑疲劳加载导致的粘结强度退化,引入折减系数δu,得到循环荷载作用下的植筋拉拔极限粘结强度τu为
(4)
δu=1.072-0.011D
(5)
式中:D为植筋直径,mm。
初滑移粘结应力τ0用式(6)计算。
τ0=δ0τu
(6)
δ0=1.720-0.056D
(7)
式中:δ0为初滑移粘结强度比例系数。
残余粘结应力τr用(8)式计算。
τr=δrτu
(8)
δr=0.574-0.021D
(9)
式中:δr为残余粘结强度比例系数。
与初滑移粘结应力τ0、极限粘结应力τu、残余粘结应力τr对应的滑移值分别为S0、Su、Sr。滑移值主要与植筋深度有关,极限粘结滑移值Su可据临界植筋深度计算得出[16]。临界植筋深度hf为
(10)
式中:fy为植筋的屈服强度,MPa。
则Su=0.054hf-9.580
(11)
初滑移值S0为
S0=0.202Su-0.086
(12)
残余滑移值Sr为
Sr=1.404Su+23.337
(13)
根据上述确定的特征值,利用文献[17]给出的方法,得到疲劳荷载作用下胶筋界面粘结滑移关系式,见式(14)。
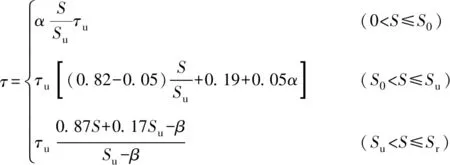
(14)
式中:Su为极限荷载Pu对应的滑移;α、β为回归系数,与植筋直径、植筋深度、疲劳加载幅度相关。
表5给出了几个特征点试验值与计算值的对比,两者之差控制在8.26%以下,式(14)结果与试验数据拟合较好。

表5 试验值与计算值对比Table 5 Comparison between the test value and the calculated value
3 结论
1)植筋深度为10d~25d的植筋拉拔试件在经历200万次荷载幅度为0.2Pu~0.45Pu的疲劳荷载后,破坏形态不发生改变,但极限荷载和初滑移荷载明显下降。植筋锚固长度大于10d的试件为钢筋拉断,其形态与普通钢筋拉拔破坏类似,具有3阶段特征。植筋深度为10d的试件拉拔至破坏图像只有上升、下降两阶段,钢筋远未达到屈服。
2)疲劳拉拔试件粘结应力降低随循环加载次数增加呈对数趋势,破坏特征不同对粘结应力下降趋势基本没有影响。
3)钢筋与植筋胶间的粘结应力沿植筋深度变化并不匀称,粘结应力峰值随荷载增加逐渐向植筋末端转移,应力大小分布也逐渐均匀。增加植筋直径和植筋深度可提高试件整体受力性能。被拔出的试件最终因胶筋界面粘结应力达到极限导致试件破坏,拉断的试件粘结应力未达到极限值。
