基于等离子体四极共振的金纳米长方体颗粒的折射率传感性能研究

刘静雅, 张现周

(河南师范大学 物理学院，光电子技术及先进制造河南省工程实验室, 河南 新乡 453007)

1 引言

局部表面等离子体激元共振(localized surface plasmon resonance, LSPR)是金属-电介质界面的自由电子在特定波长和偏振态的入射光激发下产生集体振荡，增强了纳米颗粒间的电磁近场相互作用，从而在吸收光谱或散射光谱中产生对应吸收峰或散射峰的纳米级光学现象[1]。LSPR因其在无标记检测中的优异性能而被广泛应用于电子学、光子学、光催化以及生物传感等领域。其中，LSPR在传感领域最简单的应用是利用消光光谱中的峰值移动来检测周围介质的折射率(refractive index, RI)变化[2]。在实际应用中，通常使用灵敏度(sensitivity, S)和品质因子(figure of merit, FOM)作为两个最重要的参数来评估光学传感器的传感能力，其中S表示每单位折射率的峰值位移，S=dλ(nm)/dn(RIU)，FOM定义为FOM=S(nm/RIU)/Γ(nm)，其中Γ是LSPR共振峰的半峰全宽。

近年来，诸多金纳米颗粒，如金纳米棒、金纳米双锥体和金纳米立方体等，因其具有较高的传感灵敏度和较好的化学稳定性而受到广泛关注[3-4]。为了提高LSPR传感器的S和FOM，众多科研人员通过理论或实验系统地研究了尺寸、形状、长宽比以及介电环境等因素对金纳米颗粒 LSPR特性的影响[5-8]。目前金纳米颗粒主要通过化学合成制备，尺寸通常小于200 nm[2,5,7,9-11]。随着分段合成技术的发展，金纳米颗粒的数量百分比可以达到100%且其粒径分布也可以得到很好的控制[12-13]，但通过化学方法仍难以控制金纳米颗粒的方向。通过化学合成的金纳米颗粒在胶体溶液中或沉积在衬底上时是随机取向的，而对于随机分布的非对称金纳米颗粒集体(这里的非对称是指颗粒横向结构与纵向结构不相同，例如纳米棒以及纳米双锥体等)，其中一部分颗粒的表面等离子体共振不能被定向激发。金纳米颗粒方向的随机分布将平均其LSPR的横向分量和纵向分量，使合成的不对称金纳米颗粒整体的FOM大幅度降低[14]。当金纳米棒在一定方向上嵌入到多晶硅薄膜时会引起强烈的非线性吸收[15]，我们从文献[15]的结果中可以发现定向嵌入的金纳米棒比随机分布的金纳米棒在整体上具有更窄的半峰全宽。因此可以预见，周期性排列的金纳米颗粒在改善LSPR传感器的FOM方面具有重要应用前景。

在基底表面利用光学加工方法可以制备出具有周期性结构的金纳米颗粒阵列，从而形成具有较好传感性能的超表面,而采用当前微纳加工技术制备的金纳米颗粒一般具有较大的尺寸，通常大于100 nm。当金纳米颗粒的尺寸增加时，其偶极模式共振和高阶模式共振的叠加会增加颗粒的等离子体共振线宽[16]。然而对于较大尺寸的非对称金纳米棒和纳米双锥体，其高阶谐振(特别是四级共振)会产生比偶极共振更窄的线宽，并且通过改变颗粒的长宽比，可以将共振波长调整到可见光和近红外区域[17]。因此，为了进一步提高LSPR传感器的FOM，需要对较大尺寸的非对称金纳米颗粒及其阵列四极共振的传感特性进行深入研究。随着微纳加工技术的发展，实验室已经可以实现某些简单形状的金纳米颗粒的加工，例如金纳米长方体，立方体以及圆柱体等。因此，系统地研究这些形状的金纳米颗粒的传感性能对开发新的折射率生物传感器具有重要意义。

本文通过数值模拟系统地研究了单个金纳米长方体颗粒的消光光谱以及金纳米长方体阵列的消光、透射光谱，描述了金纳米长方体尺寸对其LSPR四极共振的影响。最后，详细讨论了单个Au纳米长方体颗粒和Au纳米长方体阵列的折射率传感特性。

2 研究方法

针对尺寸远小于入射光波长的球形、椭球形以及棒状金纳米颗粒，可以采用Mie理论以及Gans理论计算随机分布粒子的光散射以及吸收特性[18]。而对于其他形状的金属纳米粒子及其阵列，尤其是当粒子的尺寸较大时，受材料、形状尺寸、周围环境介质以及粒子间相互作用等的影响，通常采用数值方法求解麦克斯韦方程得到系统的光学特性。常见的数值求解方法有T矩阵法、离散点偶极子近似法、时域有限差分法以及有限积分法等[19]。本文采用对计算机配置要求较低的有限积分法离散麦克斯韦积分方程，并通过迭代计算求解出区域的电磁场分布，从而得到系统的光学特性。麦克斯韦的积分形式如下：

(1)

(2)

另外在电磁场作用下，材料的物质方程为：

(3)

其中MS、Mμ、Mσ分别代表了材料的介电常数矩阵、磁导率矩阵以及电导率矩阵。通过物质方程、边界条件以及离散的麦克斯韦方程可以迭代求出系统的电磁场分布，并最终计算得到纳米粒子的散射截面，其中消光截面定义为纳米颗粒吸收截面和散射截面的总和：

σext=σsca+σabs

(4)

为了系统研究金纳米长方体颗粒及其阵列的消光光谱，我们利用上述方法建立了相应的计算模型。其中单个金纳米颗粒的立体图如图1(a)所示，参数l和d分别表示Au纳米长方体的长和宽，高h等于宽d。光源设置为一束电矢量平行于入射面的TM偏振的平行光，其中入射面平行于长方体的纵轴，光线入射角度默认为光线传播方向与长方体上表面的法向之间的夹角θ，其中θ的计算范围为0～80°。在单颗粒的仿真中采用开放边界，金纳米颗粒被置于折射率为n的均匀介质中，金的等离子体共振频率以及阻尼频率从Johnson和Christy报道的结果中计算得到[20]。另外在Au纳米长方体阵列的仿真中采用周期边界，尺寸形状相同的金纳米颗粒周期性地排列在玻璃板上，其中纵向周期为W1，横向周期为W2，然后将金纳米颗粒阵列和玻璃板一同置于折射率为n的均匀介质中。最后，通过消光光谱和透射光谱分别计算出了单个Au纳米长方体颗粒和Au纳米长方体阵列的折射率传感性能。

3 结果与讨论

3.1 单个金纳米长方体颗粒

图1(a)显示了单个Au纳米长方体颗粒的立体图。在单颗粒的数值计算中，首先在介质(n=1.35)中计算了长度l=500 nm、宽度和高度d=40 nm的Au纳米长方体在不同波长下随角度变化的消光光谱。其中光源为TM偏振平行光，入射角度在0～80°范围内变化。结果如图2所示，金纳米长方体在2156 nm、1118 nm和788 nm处有明显的消光峰。为了分析三个波长处产生消光峰的原因，我们监控了三个波长处的电近场分布(为了方便图片的排版，电场结果显示在图1 中)。结果如图1(b-d)所示，三个波长处的电近场振幅分布表明这三个消光峰分别由金纳米长方体的等离子体偶极共振、四极共振和六极共振激发。偶极共振和六极共振的峰值在0°处达到最大值，四极共振的峰值在40°左右达到最大值，这一现象与YONG等人报道的金纳米棒的计算结果十分相似(长度为500 nm，直径为40 nm金纳米棒的三个共振峰分别出现在2060 nm、1030 nm和734 nm处)[17]，两个模拟结果的高度相似说明了本文计算结果的可靠性。另外，从YANG等人对银纳米晶的实验中可以发现，当纳米晶的尺寸较大时，等离子体四极共振在强度上要弱于偶极共振，但四极共振的线宽小于偶极共振[21]。 从图2可以明显看出，本文计算得到的1118 nm处的四极共振在强度上确实要弱于2156 nm处的偶极共振，且其半峰全宽比偶极共振的半峰全宽小得多，与YANG等人报道的银纳米晶在360 nm处的四极共振峰的性质类似，这也进一步说明了计算结果是可靠的。另外，与金纳米棒相比，金纳米长方体具有更尖锐的边界，因此其等离子体四极共振峰将发生一定量的“红移”，这一现象与等离子体共振中的尖端形状效应具有较好的一致性[22]。

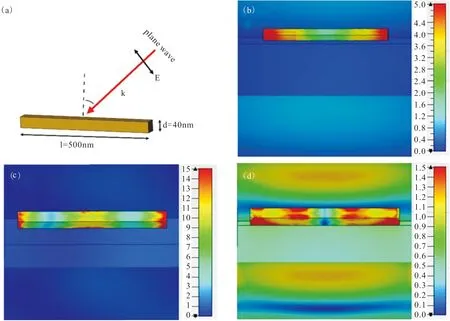
图1 数值模拟的立体结构和电场近场振幅分布。(a)单个Au纳米长方体的建模;(b-d)金纳米长方体在偶极模式、四极模式和六极模式下的电近场振幅分布Fig. 1 The configuration of the numerical modeling and the electric near-field amplitude distribution. (a) the modeling of single Au nanocuboid; (b-d) the electric near-field amplitude distribution of the Au nanocuboid at the resonances of dipole mode, quadrupole mode and sextupole mode, respectively

图2 不同入射角θ下金纳米长方体的消光光谱Fig. 2 The extinction spectra of the gold nanocuboids at different incident angles θ

为了系统地研究金纳米长方体的四极共振性质，先后对不同宽度和高度的金纳米长方体进行了消光光谱和折射率传感性质的研究。由El-Sayed[18]以及杨修春[23]等人关于金纳米棒的报道可知，当纳米颗粒的形状为棒状时，其纵向的等离子吸收峰会随着纵横比的增加发生红移。纳米长方体的结构在一定程度上与纳米棒类似，因此可以猜测，随着宽度和高度的减小，纳米长方体的纵横比会增大，其共振峰也将发生一定的红移。图3(a)中的计算结果表明，纳米长方体的偶极共振的共振波长的确随着颗粒宽度的减小产生了不同程度的红移，共振强度也得到了一定的增强，与报道的金纳米棒的计算结果[18]具有相似的变化规律。同时图3(b)表明，与偶极共振类似，纳米长方体的四极共振共振波长也会随纵横比的增加产生一定的红移, 且颗粒宽度越小，红移的程度越大。根据等离子体共振峰的传感特性，即共振波长越长，其折射率灵敏度越高[24]，可以预测，宽度较小的金纳米长方体将具有更高的灵敏度。此外从图3(b)可以发现，随着宽度的减小，纳米长方体的四极共振峰逐渐增强，且半峰全宽逐渐减小，然而值得注意的是，当颗粒宽度从50 nm减小到40 nm时，其四极共振峰强度变弱，且半峰全宽明显增加。因此可以认为，长度为500 nm的金纳米长方体在宽度为50 nm左右时，可以得到强度最高、半峰全宽最佳的四极共振。

图3 长度相同(l=500 nm)、宽度不同的金纳米长方体偶极共振(a)以及四极共振(b)的消光光谱Fig. 3 The extinction spectra of the gold nanocuboids with same length (l=500 nm) and different widths at the resonances of dipole mode and quadrupole mode, respectively

为了直观地说明不同宽度对金纳米颗粒传感性质的影响，通过改变介质的折射率计算了金纳米颗粒在1.33～1.37折射率范围内的传感性能(S和FOM)。如图4和图5所示，金纳米长方体的四极共振灵敏度随宽度的增大而减小，这与上述预测吻合较好。而d= 50 nm的纳米长方体的FOM要大于d= 40 nm的纳米长方体，这主要是由于d=50 nm时共振峰的半峰全宽较窄。值得注意的是，单个金纳米长方体的FOM可以达到11.5，远大于表1中所示的金纳米棒和金纳米双锥体在相似共振波长下的结果。这说明：当类似金纳米棒等的圆端变为类似Au纳米长方体等的方端时，四极共振将具有更高的灵敏度和FOM。

图4 金纳米长方体颗粒在长度相同(l=500 nm)时，不同宽度下的折射率传感消光光谱Fig. 4 Refractive index sensing performance of the gold nanocuboids with same length (l=500 nm) and different widths

图5 具有不同宽度的单个金纳米长方体颗粒和纵向周期W1 = 800 nm，横向周期W2 = 600 nm的Au纳米长方体阵列的峰值波长λ与折射率n的关系Fig. 5 Peak wavelengths λ as a function of the refractive index n for the single gold nanocuboid with different widths and the Au nanocuboid arrays with the longitudinal period W1=800 nm and the transverse period W2=600 nm

3.2 金纳米长方体阵列

通过将金纳米长方体周期性地排列在玻璃板上，再整体置于均匀介质中，然后改变介质的折射率计算了基于等离子体四极共振的金纳米长方体阵列的折射率传感性能。图6(a)给出了周期化金纳米长方体阵列的立体图，纳米颗粒之间采用周期边界条件，入射光为偏振方向与入射面平行的TM波，入射角度固定为40°。金纳米长方体阵列的纵向周期W1=800 nm，横向周期W2=600 nm。图6(b)所示的金纳米长方体阵列在共振波长处的电近场振幅分布表明，该阵列的共振模式为四极共振。金纳米长方体阵列在不同折射率下的消光和透射光谱如图7所示。可以发现，随着折射率的增加共振波长位置与单颗粒产生相似程度的红移。在以往的研究中，纳米颗粒一般处在胶体中或随机沉积在基底上，纳米颗粒的随机取向对其消光谱线宽进行了平均，极大地影响了其传感的FOM。如表1和表2所示，Au纳米长方体阵列的灵敏度S≈787.72nm / RIU和FOM≈13.82，均优于表1中的单颗粒和表2中所示的纳米颗粒集体的传感性能。在金纳米长方体阵列中观察到的这种高FOM应该归因于不对称纳米颗粒方向的一致性。由于利用光刻技术可获得由较大尺寸金纳米长方体阵列构成的折射率传感器，并可方便地应用于实际应用中，因此这将为提高LSPR生物传感器的品质因子提供重要的理论依据。

图6 数值模拟的结构和金纳米长方体阵列的电场近场振幅分布Fig. 6 The configuration of the numerical modeling and the electric near-field amplitude distribution of Au nanocuboid arrays

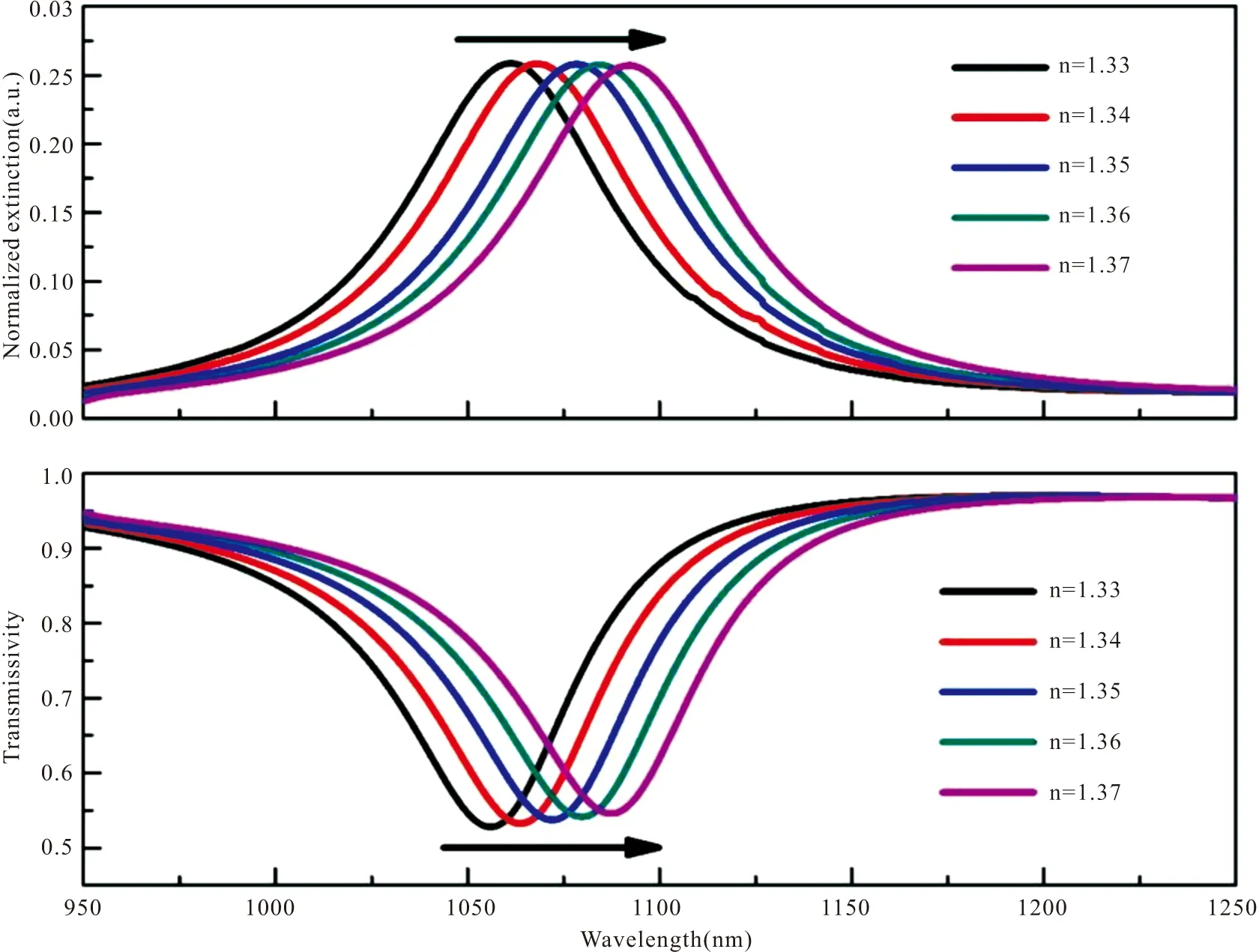
图7 金纳米长方体阵列在不同折射率下的消光和透射光谱Fig. 7 The extinction and transmission spectra of the Au nanocuboid arrays under different refractive indexes

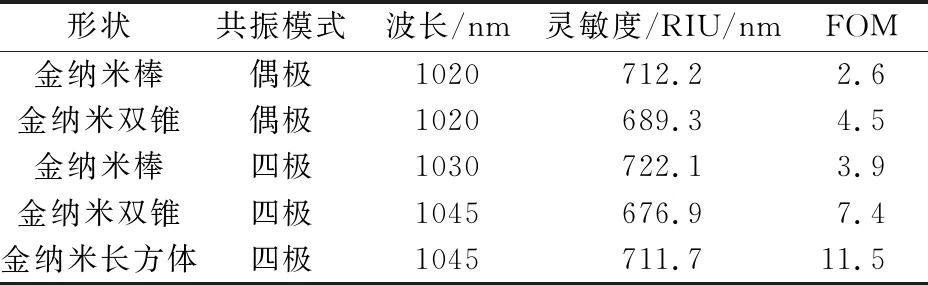
表1 不同共振模式下金纳米棒、金纳米双锥体[17]以及金纳米长方体折射率传感性能对比Table.1 Comparison of RI sensing properties among three kinds of single paticle (Au nanorod, Au nanobipyramid [17] and Au nanocuboid) in different resonance modes

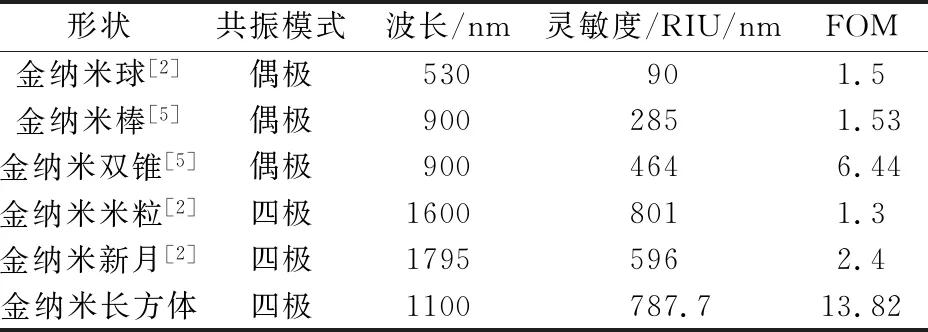
表2 不同金纳米颗粒集体与金纳米长方体阵列间的折射率传感特性对比Table.2 Comparison of RI sensing properties among different nanoparticle ensembles and the Au nanocuboid array

4 结论

本文系统地研究了单个金纳米长方体颗粒和金纳米长方体阵列的折射率传感性能。结果表明，对于较大尺寸的不对称金纳米颗粒，四极共振的半峰全宽远小于偶极共振的半峰全宽。当金纳米颗粒类似于金纳米棒的圆形末端变为类似于长方体的方形末端时，也就是当金纳米颗粒的边界变得尖锐时，其四极共振峰将发生一定程度的红移，且该四极共振会具有更高的折射率灵敏度和FOM。在给定长度为500 nm时，宽度在50 nm左右的单个金纳米长方体的四极共振具有最佳的FOM。金纳米长方体阵列四极共振时的灵敏度和FOM可以达到787.72 nm /RIU和13.82 nm /RIU，这将为提高LSPR生物传感器的灵敏度和FOM提供重要的理论依据。