特征点检测DoG并行算法

朱 超，吴素萍

宁夏大学 信息工程学院，银川 750021

1 引言

异构计算环境下高效算法的研究是大数据关键问题的重要内容。大数据计算模式与大数据计算方法主要研究分布式环境下的大数据分析与处理的新型计算模式与高效基础算法，包括分布实时计算问题（分布并行的计算架构与编程新模型、分布式计算的可行性理论、大数据算法设计等），现代超算问题（异构计算环境下的计算优化、多粒度分布式并行环境下的新编程模型、大数据超算算法等），非结构化信息处理，多源异构信息融合。

高性能计算技术迅速发展，目前已成为解决大数据量问题的有效方式。同时，异构并行系统已成为当前高性能计算机系统发展的重要趋势之一，在众多异构混合平台中，基于CPU 和GPU 异构计算平台具有很大的发展潜力。

特征点检测被广泛应用于目标识别与跟踪、三维重建、图像拼接等视觉领域[1-6]。现阶段，图像局部不变特征的检测及匹配算法取得了很好的效果。尺度不变特征变换（Scale-Invariant Feature Transform，SIFT）[7]具有尺度和旋转不变性，SIFT 描述子用三维直方图对特征一定领域中像素点梯度的方向与模值进行统计，具有很强的抗噪声能力，但是由于维数较高，使得进行图像匹配时速度较慢。为了解决SIFT 算法的时效性，Bay 等[8]提出了一种加速鲁棒性算子（Speeded Up Robust Features，SURF），SURF描述符维数低，速度较快，但是无法保留大量的较稳定的特征点，会导致重建过程中依据匹配特征点生成的三维点云较稀疏。Harris角点检测[9]是最著名的基于图像灰度值的特征点提取方法，但不能保证尺度不变。高斯差分（Difference-of-Gaussian，DoG）算法同时在二维平面空间和尺度空间检测局部极值作为特征点，这种特征点具备良好的稳定性，满足尺度不变。Harris算法趋向于提取梯度变化剧烈的点，而DoG算法一般提取均匀区域的中心点，也称斑点。针对Harris算法文献[10]提出了一种基于OpenCL设计思想的并行算法，相比CPU加速比可达77倍。文献[11]利用OpenCL技术对SIFT 算法进行加速，大大降低了原算法的耗时。文献[12]提出了一种基于GPU 和CPU 异构计算平台的Canny并行算法，相比CPU加速比可达5.39倍。文献[13]提出了一种基于GPU的HOG（Histogram of Oriented Gradient）特征提取与描述算法，相比CPU获得了40 倍左右的加速。文献[14]提出了一种基于DAGS+GPU的去块滤波算法，相比串行获得了11～24倍的解码加速比。文献[15]提出了一种基于OpenCL 架构的SURF并行实现方法，对不同分辨率的图片均实现了10倍以上的加速比，一些高分辨率的图片甚至可以达到39.5 倍。文献[16]提出了一种基于CPU 多线程和GPU两级粒度并行策略，其中特征提取最高加速13 倍。文献[17]在求取点云特征时提出了一种基于OpenCL实现的点云分割算法，利用OpenCL 的并行处理能力，使得运行效率为基于CPU实现的16倍。

基于DoG特征点检测算法研究主要是基于CPU串行架构，算法性能的提升效果不理想，不能很好地满足实时处理。另一方面，三维重建中运算量大，特征点检测效率较低，为了提高特征点检测的效率，本文在目前主流的多核CPU、CUDA 及OpenCL 架构上，提出三种DoG特征点检测的并行算法，给出不同并行架构环境下的并行算法，实现特征点检测的多平台并行算法，提高特征点检测效率和多平台可应用性，实现特征点检测的多核CPU和GPU并行算法。本文给出的特征点检测并行算法是在彩色图像上直接进行并行化，不同于其他在灰度图上进行，或者将彩色图像先转换为灰度图像再进行的方法。本文算法获得了较高加速比，最高可获得96倍多的加速比，并具有良好的数据和平台可扩展性，可有效提升特征点检测和三维重建过程的效率。

2 特征点检测并行算法

DoG 算法在考虑尺度不变性的同时减小了特征点检测过程中LoG（Laplace of Gaussian）算法的计算复杂度。DoG对高斯函数进行差分运算，高斯函数二维表示为：

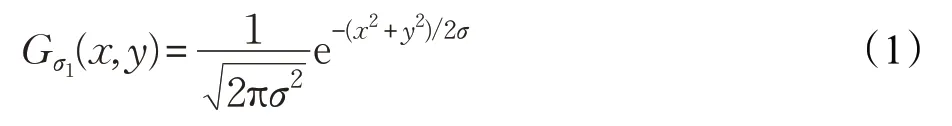
首先使图像与高斯函数进行若干次卷积运算，每次运算对模糊因子赋不同值，创建高斯尺度空间：

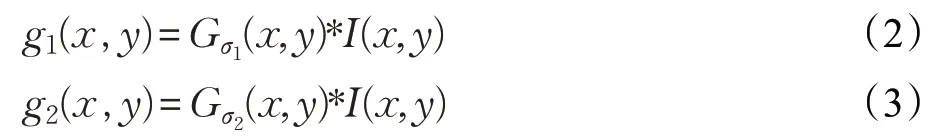
这里g1(x,y)为高斯滤波后图像，I(x,y)为原始图像。

然后使高斯尺度空间中紧邻的两幅图像进行减法运算，创建出高斯差分尺度空间，即DoG 尺度空间，公式表示为：

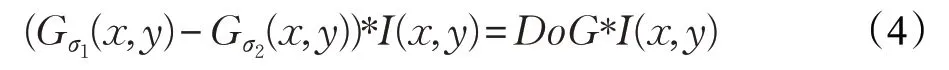
即可将DoG表示为：

即：

DoG空间中局部极值点即为特征点。如图1所示，将图中所标记的点分别与该点本层尺度邻近8 个点以及上下层尺度各9个点共27个点进行比较，若该点为极值点，则确定为特征点[6]。

图1 寻找极值点

2.1 算法步骤

算法主要是创建DoG尺度空间，并进行比较，判断是否为极值点，若为极值点，则确定为特征点。

特征点检测步骤如算法1。

算法1 DoG特征点检测算法

输入：图像，高斯模糊因子。

输出：图像特征点数量，每个特征点坐标。

（1）初始化图像。将图像数据读入到一维image 数组，为保证计算精度，算法中将一维image 数组转换为三通道。浮点型二维数组存储在m_image数组中。

（2）创建高斯尺度空间。使输入图像与不同模糊因子所对应的高斯函数进行指定次数的卷积运算，创建图像的高斯尺度空间，对图像每个点卷积处理可独立进行。

（3）创建DoG 尺度空间。对（2）中所创建的高斯尺度空间，对紧邻两幅图像进行减法运算，得到图像的DoG尺度空间。

（4）判断是否为极值点。在（3）所创建的DoG 尺度空间中，使每一个点与本层以及上下层相邻点进行比较，求得的极值点即为特征点。

2.2 OpenMP并行算法

OpenMP 是由OpenMP Architecture Review Board所推出的，基于共享内存的一套多线程程序设计指导性的编译处理方案。OpenMP可移植性高，可扩展性好[18]。

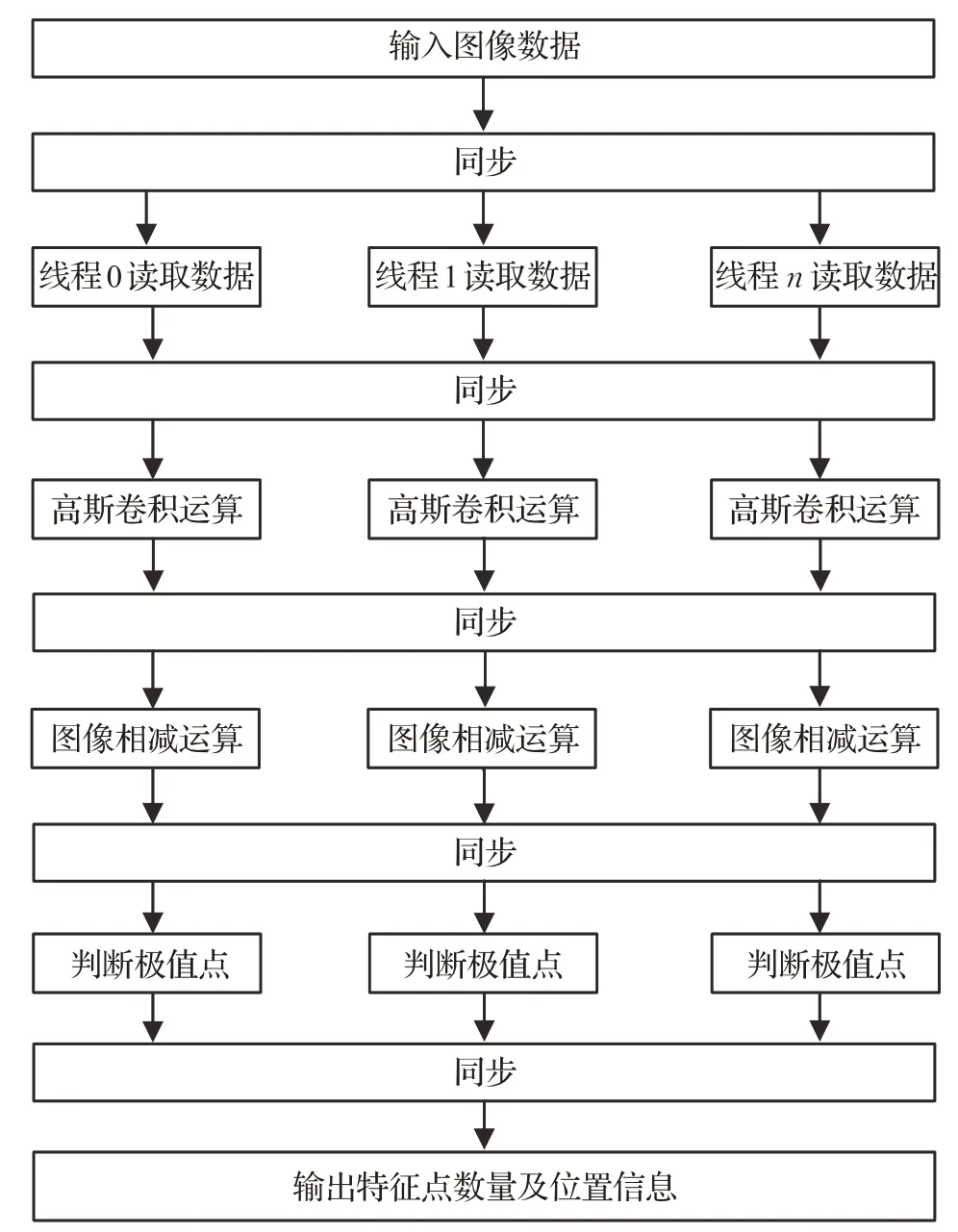
图2 基于OpenMP的DoG算法流程

通过合理的任务分配和同步，可保证计算任务的均衡性和正确性。在图2中，使用Fork-Join[18]执行模式，读入图像数据后，当程序执行到图像初始化并行域时会生成多个从线程，执行完毕后从线程合并为一个主线程，步骤之间需要同步来确保本步骤的完成和下一个步骤的正确性。

特征点检测并行算法如算法2。

算法2 基于OpenMP的并行算法

输入：图像，n个不同尺度的高斯卷积模板，尺度由标准差σi确定。

输出：图像特征点数量，每个特征点坐标。

（1）生成与CPU核数相同数量的线程，创建并行区。

（2）进行循环任务的分配，在并行算法中图像被划分为与线程数相同数量的区域，每一个区域由（1）中所生成的线程进行处理，一个线程完成所负责区域图像的初始化，高斯卷积相减(n-2)，判断是否为极值点一系列任务，找出该区域中的特征点。

在多核CPU中，在调用的最内层进行并行，派生线程与合并线程次数会减少，也会使时间开销降低，相对于在外层进行并行或在两层都进行并行时速度会有所提升。

2.3 CUDA并行算法

计算机统一设备架构（Computer Unified Device Architecture，CUDA），是由 NVIDIA 公司推出的一种GPU 并行计算框架，能够利用GPU 的计算能力提供一套高效的密集型数据计算解决方案[19]。

CUDA 模型为CPU 端完成串行及调度工作，GPU端为多个线程并行执行内核函数完成计算工作。GPU线程采用块状划分，即所有的线程以二维方式组织，线程与图像中的像素点一一对应。开始由CPU端将数据拷贝至GPU端，调用内核函数进行计算，计算完成后再将结果拷贝至CPU端。基于CUDA的DoG特征点检测过程如图3所示。

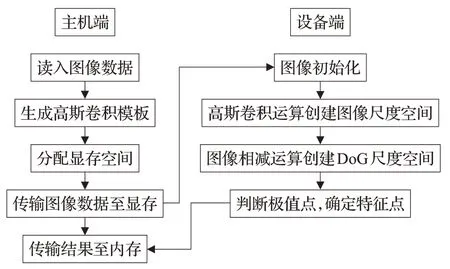
图3 基于CUDA的DoG算法流程

并行特征点检测算法步骤如算法3。

算法3 基于CUDA的并行特征点检测算法

输入：图像，高斯模糊因子。

输出：图像特征点数量，每个特征点坐标。

主机端：

（1）高斯模板初始化，创建n个不同尺度的高斯卷积模板尺度由标准差σi确定。

（2）配置block：blockSize=16×l6，即一个block 含有256个thread。

（3）开辟显存空间，把图像数据保存至image数组，把数据传输至GPU显存。

（4）DoG 特征点检测，主要由主机端进行调度，在GPU端并行执行，其步骤如（4.1）～（4.11）所示：

（4.1）进行图像的初始化。调用GPU端计算每个线程的全局坐标，与将要处理对应像素点的关系，取到该线程所要处理的像素点，进行数据类型的转换，完成图像初始化任务。

（4.2）创建不同模糊因子所对应的高斯模板，并拷贝至GPU端。

（4.3）取到本线程对应处理的像素点，对该像素点分别进行x方向、y方向的高斯模糊运算，即g1(x,y)=，其中表示标准差为σ1的高斯滤波模板，I(x,y)为原始图像，计算出模糊后的结果存储在数组中，即第一层模糊图像。

（4.4）计算出第二层高斯模糊图像，即g2(x,y)=2，其中表示标准差为σ2的高斯滤波模板，把结果存储在数组中。

（4.8）此时已经得到两层DoG 空间，即第一层DoG空间及第二层DoG空间。

（4.9）继续迭代执行（4.7）、（4.8）得到第三层高斯差分尺度空间，此时在第二层DoG空间中，即可判断本线程所对应的像素点在本层尺度邻近8 个点和上下相邻两层尺度各9个点共27个点中是否为极值点，若为极值点，则确定为特征点。继续迭代执行（4.7）、（4.8），每得到一层DoG 空间后即可进行极值点的判断，并确定是否为特征点。

（5）把结果拷贝至主机端。

（6）释放GPU显存。

并行算法的具体实现过程为：将整个检测过程分解为若干子任务，一个子任务由一个对应的global函数进行处理，算法运行过程中，global 函数与grid 一一对应，grid 将任务分配给 block，block 再分配给 thread 进行处理，所有函数都由主机端进行调用，在GPU端运行。

2.4 OpenCL并行算法

OpenCL 模型是针对异构平台编程的开放工业标准，OpenCL有一套完整的并行程序编写框架，由程序设计语言、函数库、运行时系统、API几部分构成[20]。

OpenCL 平台模型为一主机加多OpenCL 设备。一个OpenCL设备又由多个计算单元（CU）组成，而一个计算单元又可分解为多个处理单元（PE），处理单元用来进行计算。主机端完成OpenCL程序的开始和终止，分配计算资源[20]。

OpenCL执行模式为CPU端主要完成平台初始化、设备选择、创建执行上下文、设置工作空间与启动Kernel等任务。GPU端并行完成Kernel执行等任务。

基于OpenCL的DoG特征点检测算法步骤如算法4。

算法4 基于OpenCL的并行特征点检测算法

输入：图像，高斯模糊因子。

输出：图像特征点数量，每个特征点坐标。

主机端：

创建平台对象；获得平台相关设备；由设备得到上下文；由上下文生成命令队列；设置工作节点个数，创建和设置 Kernel，执行 DoG 算法中的 Kernel，进行 DoG 特征点检测。

并行算法的具体实现过程为：将整个检测过程分解为若干子任务，分别完成图像初始化操作，图像模糊操作，即；图像相减操作，即D=，计算出该像素点的DoG值；图像的多次迭代模糊运算；寻找极值点操作。子任务与Kernel一一对应，在工作节点中进行运算。

为了使硬件性能得到充分发挥，本文选择将工作组大小设置为16×16，即一个工作组包含256个工作节点。

不同于灰度图，本文是在三通道彩色图像上进行特征点检测的并行化，即R 通道、G 通道、B 通道。不仅需要计算线程或工作节点与图像中的像素点对应关系，还需要计算线程或工作节点与图像中的一个像素点中每个通道的对应关系，由主机端传输至GPU 端的图像数据是一个一维数组的结构，如图4所示。

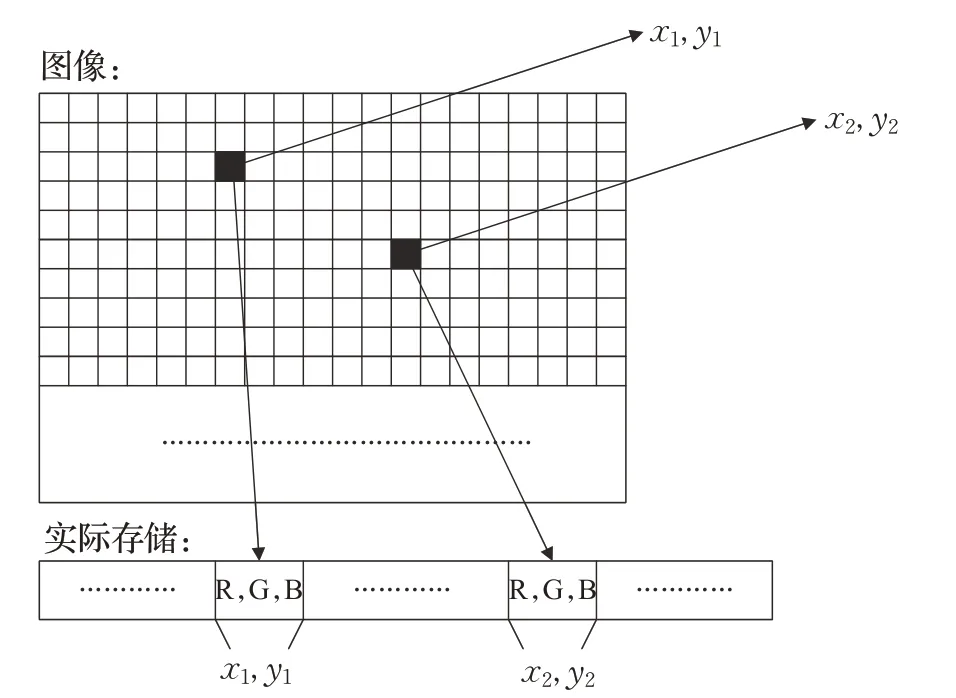
图4 图像中像素点与实际存储位置对应关系图

在图4中，(x1,y1)、(x2,y2)为图像中的任意两点，图像的每一像素点实际存储该点的RGB 三通道值，即图像中每个点需要存储三个值。CUDA 与OpenCL 架构中，线程或工作节点与像素点为一对一的处理关系，本文算法根据线程的位置计算出对应处理点的三通道值，具体计算公式为公式如下：

其中，blockIdx.x为线程块编号，blockDim.x为线程块大小，threadIdx.x为线程块内线程编号。通过式（6）首先计算出该线程对应处理像素点的R通道值所在位置，然后再依次通过式（7）与式（8）计算出该像素点的G 通道值与B 通道值所在位置。

3 实验测试与结果分析

由于并行算法实验环境，没有统一的配置环境，在比较并行算法的性能时，主要是将并行算法的实验结果与串行算法的实验结果进行比较，主要比较的指标为：（1）并行算法与串行算法相比较所取得的加速比。（2）并行算法的可扩展性，包括数据可扩展性和平台可扩展性。数据可扩展性指在同一硬件平台下，并行算法随着实验数据量增大，相应的加速比也在增大。平台可扩展性指在同一类型平台下并行算法随着平台配置的提高，相应的加速比也随着在提高。（3）并行算法的精度，主要指并行算法一般要保证串行算法的精度。本文实验主要从上述三方面进行比较。

3.1 实验环境

（1）硬件

平台1：CPU（2 核）为Pentium Dual Core T4300@2.10 Hz；显卡为NIVIDA GeForce G210M。

平台2：CPU（6 核）为 Intel Xeon E5-2620@2.00 GHz；显卡为NVIDIA Tesla C2070。

（2）软件

操作系统：Windows-7。

开发环境：VisualStudio2010、CUDAToolkit6.5、OpenCLl.0。

3.2 实验测试图像用例

本文选取kermit、hallFeng 两组图像数据集作为实验数据集。该数据集来源于PMVS（基于面片的三维多视角立体视觉算法）主网，其中kermit 为一组从不同角度对青蛙模型拍摄的连续图像，hallFeng 为一组从不同角度对一座大楼拍摄的连续图像，如图5所示。

图5 测试图像

3.3 测试结果与分析

本文对两组数据集在串行、基于OpenMP 多核并行、基于CUDA并行架构、基于OpenCL并行架构下分别进行特征点检测测试，记录各算法执行时间并进行分析。

3.3.1 标准测试图像数据可扩展性实验

实验分别从kermit图像数据集与hallFeng图像数据集中选取标准图像，对图像进行降采样处理，取得多张尺寸大小不同的图像，用以进行对比实验。

针对尺寸大小不同的图像，在实验平台1上分别进行了算法运行耗时统计，为保证测试时间准确性，实验结果取10次测试时间的平均值。实验记录结果如表1、表2所示。

为更直观表现在不同数据集上算法在串行与在不同并行架构上的运行时间，绘制柱状图6 和图7。从图中可以看出，DoG并行算法相比较串行算法的运行时间大幅度降低。基于CUDA 和OpenCL 的并行算法的运行时间更少，两种环境下的并行算法具有基本相同的性能，说明本文基于CUDA和OpenCL的并行算法是稳定的。基于OpenMP 算法的加速比接近CPU 核数。基于CUDA的并行算法和基于OpenCL的并行算法对kermit图像，最高加速比达到36倍多，对hallFeng图像，最高加速比可达到40倍多。加速比随图像大小的增加呈现明显上升趋势，都表现出很好的加速效果，并行算法表现出较好的数据可扩展性。

表1 kermit图像实验结果

表2 hallFeng图像实验结果

图6 kermit数据集运行时间柱状图

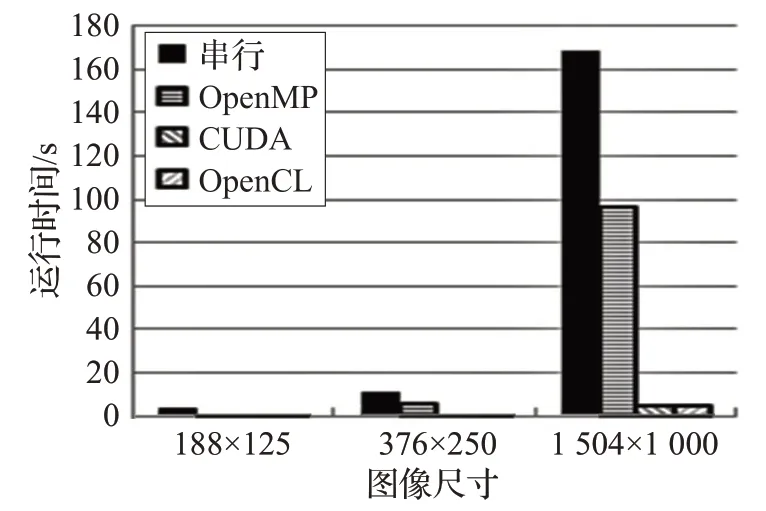
图7 hallFeng数据集运行时间柱状图

为能直观展现算法在不同并行架构下加速性能，本文计算出DoG算法在不同并行架构下的运行时间和在串行算法运行时间的比值，求取加速比，绘制出加速比曲线图，如图8、图9 所示。从图中可以看出，在一定范围内，加速比随着图像大小的增加呈上升趋势，两种并行算法都表现出了较好的数据可扩展性，在数据较大时基于OpenCL的并行算法加速较快一点。

图8 kermit图像并行加速比曲线图

图9 hallFeng图像并行加速比曲线图

3.3.2 CPU多核可扩展性实验

本小节对并行算法的多核可扩展性进行实验与分析，分别在两数据集中选取一张测试图片，尺寸固定，分别在 2 核 CPU 与 6 核 CPU 上做基于 OpenMP 的 DoG 并行算法可扩展性实验，对运行时间进行统计，并计算加速比，结果如表3所示。

表3 kermit和hallFeng图像不同平台多核CPU实验结果

为了直观进行观察，计算出不同平台多核CPU 并行算法加速比，绘制曲线图10。从图中可以看出，加速比随着CPU 核数的增加呈上升趋势，并且加速比曲线相对来讲较为陡峭，也就是说加速比提高相对也较快，表明本文并行算法表现出较好的多核可扩展性。

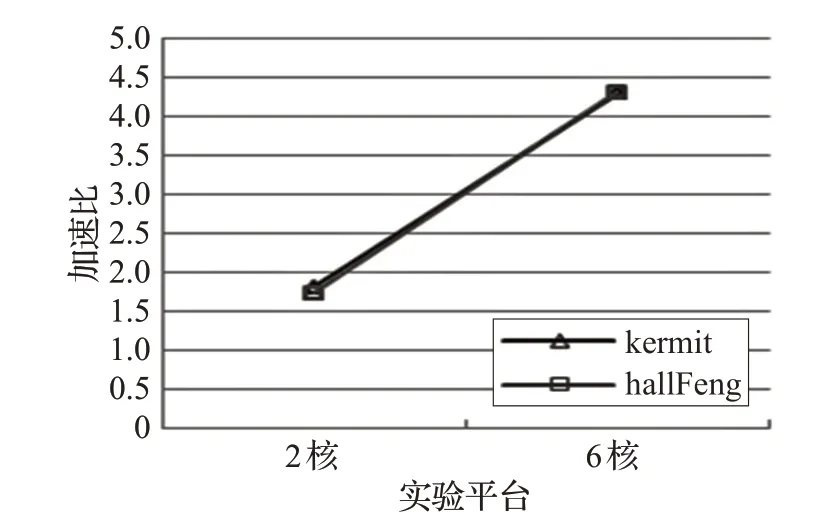
图10 kermit和hallFeng图像不同核数（平台）多核CPU实验结果

3.3.3 并行算法GPU平台可扩展性实验

为验证本文并行算法具备良好的可移植性，即GPU平台可扩展性，在具有较高计算能力的GPU 上同样可以达到较高的性能。在hallFeng中选取一张测试图片，尺寸为 752×500，在 NIVIDA GeForce G210M 显卡与NVIDIA Tesla C2070显卡上进行特征点检测并行算法实验，对算法运行时间进行统计，并计算加速比，结果如表4所示。

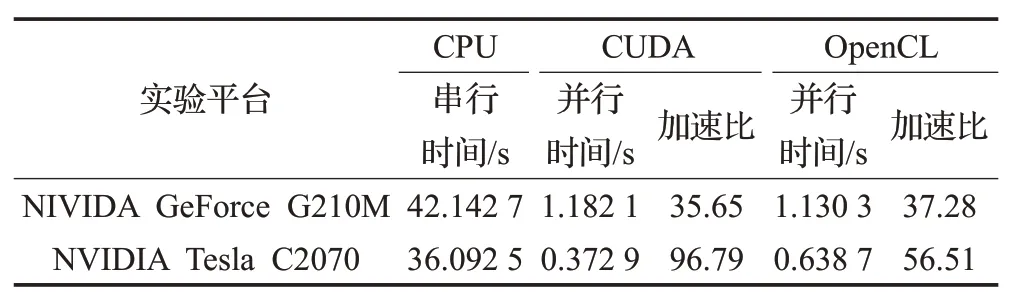
表4 hallFeng图像不同平台CUDA和OpenCL实验结果

为了直观观察实验结果，绘制出曲线图11。从图中可以看出，将算法在计算能力为1.2的NIVIDA GeForce G210M上的加速比与在计算能力为2.0的NVIDIA Tesla C2070 上的加速比进行比较，加速比最多提升了两倍多，说明本文并行算法在GPU 上具有良好的可移植性和可扩展性。

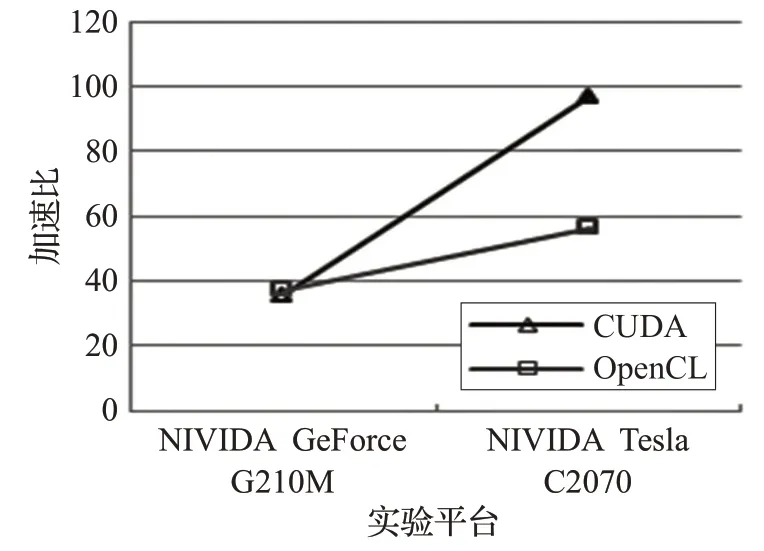
图11 hallFeng图像不同平台CUDA和OpenCL实验结果

3.3.4 Tesla C2070 GPU上数据扩展性实验

为验证本文的并行算法在Tesla C2070显卡上具有数据可扩展性，对hallFeng 数据集不同尺寸图像在NVIDIA Tesla C2070显卡上进行并行特征点检测算法实验，统计算法耗时，计算出加速比，结果如表5所示。

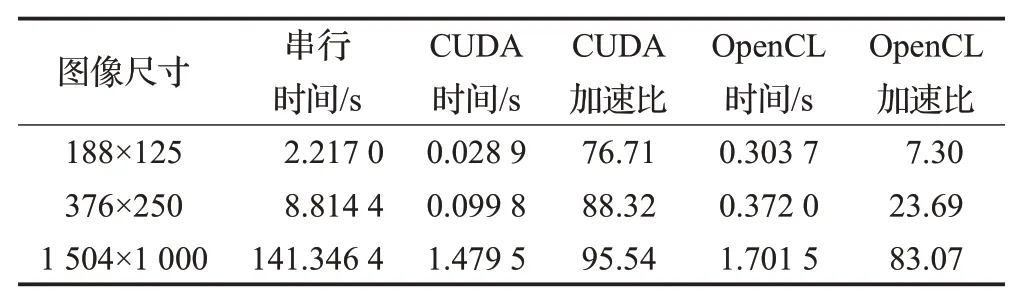
表5 Tesla C2070平台上hallFeng图像DoG实验结果

为了直观观察实验结果，绘制曲线图12。可以看出，hallFeng数据集中图像尺寸从188×125扩展到1 504×1 000 时，两种并行算法加速比曲线呈上升趋势，基于CUDA 并行算法在小数据量时加速效果也很好，逐渐趋于稳定。当图像尺寸增大时，数据量增多，数据的传输延迟也会延长，计算时间对传输延迟的隐藏性也逐渐减弱。基于OpenCL并行算法加速比从7.3倍提升到83.07 倍。两个并行算法最高加速比超过95 倍。加速比随着图像数据量的增大呈现出上升趋势，说明并行算法在NVIDIA Tesla C2070显卡上具有较好的数据可扩展性。

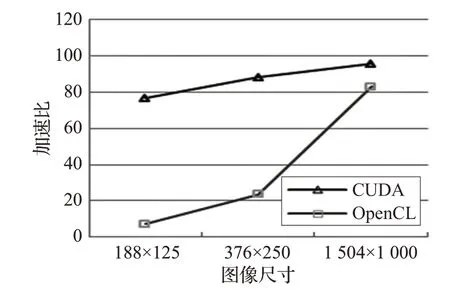
图12 Tesla C2070平台hallFeng图像DoG并行加速比曲线图

从本文的实验结果可以看出，在GPU 环境下本文基于CUDA 和基于OpenCL 的并行算法都具有很好的加速效果。OpenCL 是一个开放的行业标准，可运行在通用GPU上。CUDA由NIVIDA开发，可运行在NIVIDA平台上。

3.4 并行算法精度分析

特征点检测并行算法在速度获得大幅度提高的同时，必须确保检测的准确度。本文统计出在OpenMP、CUDA、OpenCL并行框架下检测出的特征点的数量，如表6、表7所示。

表6 kermit特征点检测数量

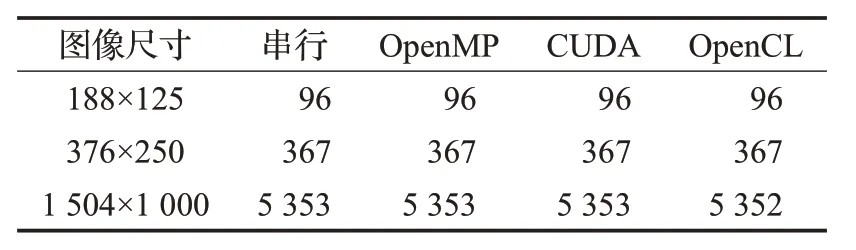
表7 hallFeng特征点检测数量

从表6、表7 中可以看出，并行算法在基于OpenCL架构下，只在hallFeng数据集中图像尺寸大小为1 504×1 000 的情况下，与串行算法比较，少检测出一个特征点，准确率达99.9%以上，而在其余情况下，并行算法检测出的特征点数量与串行算法检测出的数量及位置信息完全相同，准确率可达100%。表明本文所提出的特征点检测并行算法不仅大幅度提升了特征点检测的速度，同时也保证了特征点检测的精度。

4 结束语

本文提出了基于OpenMP 多核CPU 并行算法和基于CUDA及OpenCL并行架构的GPU环境下并行算法，实验结果表明基于多核CPU，特别是GPU的并行算法，能够大幅度提高特征点检测的执行速度。随着CPU核数增加，加速比也在增加，算法表现出良好的多核可扩展性。随着图像数据增大，算法的加速比呈上升趋势，表现出良好的数据和平台可扩展性。基于GPU的DoG特征点检测并行算法最高可取得96倍多的加速比。