混沌精英质心拉伸机制的樽海鞘群算法

陈忠云，张达敏，辛梓芸，张绘娟，闫 威

贵州大学 大数据与信息工程学院，贵阳 550025

1 引言

大自然充满执行不同任务的社交行为，虽然所有个体和群体行为的最终目标是生存，但生物在群体中进行合作和互动有以下几个原因：狩猎、防御、导航和觅食。多种动物和昆虫的智能群体行为多年来引起了研究者的关注。计算机科学研究人员将这些群体模型作为解决复杂现实世界问题的框架，从而产生了人工智能的一个分支，通常被称为群体智能。目前已经提出了许多的智能优化算法，例如遗传算法（Genetic Algorithm，GA）[1]、粒子群优化算法（Particle Swarm Optimization，PSO）[2]、蝴蝶优化算法（Butterfly Optimization Algorithm，BOA）[3]等。这些算法已成功应用于各种科学领域，如过程控制、生物医学信号处理[4]、图像处理以及许多其他工程设计问题[5]。

樽海鞘群算法（Salp Swarm Algorithm，SSA）是2017 年由Mirjalili 等人提出的一种新型启发式智能算法[6]。樽海鞘群算法具有结构简单、参数少、容易实现等优点，受到国内外专家学者广泛关注，已被成功应用到多目标优化和工程设计问题[6-7]。虽然樽海鞘群算法在求解大部分优化问题时具有优越性，但是与其他群智能算法一样，仍然存在求解精度低和收敛速度慢等缺陷。文献[8]将樽海鞘群算法中跟随者单步位置更新方式改为两步，分别根据自适应平局移动策略和领域最优引领策略进行更新，之后在引入方向学习策略以一定概率对个体位置进行扰动，提高种群多样性，使算法跳出局部最优。文献[9]提出固定惯性权重，可以加快搜索过程中的收敛速度，并应用特征选择问题。文献[10]把樽海鞘群算法和混沌理论相结合提出混沌樽海鞘群算法，在解决特征提取问题时，能发现最优特征子集，最大程度地提高分类精度，最小化所选特征的数目。文献[11]提出基于樽海鞘群算法的无缘时差定位，利用SSA 解决TDOA（Time Difference of Arrival）定位结算问题，验证算法在多站时差定位问题上的有效性与优越性。文献[12]提出基于Tent映射的灰狼优化算法，通过混沌映射产生初始种群，增加种群个体的多样性。文献[13]提出自适应Tent混沌搜索的蚁狮优化算法，自适应调整混沌搜索空间得到最优解，改善适应度较差个体，提高种群整体的适应度和寻优效率。文献[14]改进Tent 映射，具有更优越的混沌特性，能更好地实现混沌寻优。文献[15]选择精英个体进行反向学习，拓展种群的搜索区域，增强多样性和加速收敛。文献[16]提出重心方向学习（Centroid Opposition-Based Learning，COBL），以整个群体重心为参考点计算反向点，这样反向点包含了群体搜索经验。

受上述文献的启发，本文提出了一种改进混沌精英质心拉伸机制的樽海鞘群算法，以解决标准樽海鞘群算法存在的求解精度不高和收敛速度慢等问题。通过改进Tent映射来生成樽海鞘群算法的初始种群，增强初始个体的均匀性。种群个体更新后，选择部分精英个体并采用质心拉伸机制，有利于搜索更多的有效区域来提高群体的多样性，增强算法的全局探索和局部开发能力。通过求解多种维度的12 个典型复杂函数以及部分CEC2014函数的最优解来验证混沌精英质心拉伸机制樽海鞘群算法（Chaotic and Elite centroid stretching mechanism Salp Swarm Algorithm，CESSA）的有效性。

2 樽海鞘群算法

樽海鞘群算法[6]是Mirjalili 等人揭示的一种全新的智能优化算法，这种算法的思想出自于樽海鞘的聚集行为，即樽海鞘链。樽海鞘以水中的浮游植物（海藻等）为食，通过吸入喷出海水完成在水中的移动。在樽海鞘群算法中，樽海鞘链由两种类型的樽海鞘组成：领导者和追随者。领导者位于樽海鞘链的最前面，而其他个体则为追随者的角色。

樽海鞘的种群行为与其他算法有所不同，其并不是以“群”分布，而是采用头尾连接的形式，组成“链”的形态，顺次跟随着移动。樽海鞘链中的领导者排在队伍的最前端，它对环境有着最优的判断，但与其他群智能算法不同的是，领导者不会直接影响整个种群的移动方向，而是直接影响紧接着的第二个樽海鞘个体的位置更新，第二个个体影响第三个个体，以此类推。因此，领导者的位置对其余樽海鞘位置影响程度会顺位递减，这使排在后面的个体有着更好的多样性。

在樽海鞘群算法中，定义每个樽海鞘个体的位置矢量X用于在N维空间中搜索，其中N是决策变量的数目。樽海鞘群算法中位置向量X将由维度为d的N个樽海鞘个体组成。因此，种群向量由N×d维矩阵构成，如下公式所示：

在樽海鞘群算法中，食物源的位置是所有樽海鞘个体的目标位置。因此，领导者的位置更新公式如下所示：

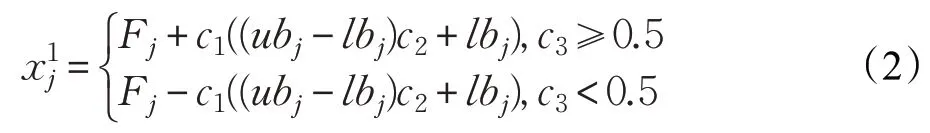
由式（2）可知，领导者位置更新主要受到食物源位置影响。系数c1是樽海鞘群算法中最重要的参数，可以使SSA 的探索能力和开发能力处于平衡状态，其定义如下：

式中，t为当前迭代次数，Tmax为最大迭代次数。

在求解测试函数优化问题中，搜索范围变化大。为了使樽海鞘群算法前期搜索具有更好的全局性和随机性，本文选取多个领导者来进行更新，但领导者太多，算法随机性较强，这会导致算法稳定性降低，因此为了权衡算法的随机性和稳定性，本文选取一半的樽海鞘个体作为领导者。

为了更新追随者的位置，使用以下公式（牛顿运动定理）：

因此，由式（2）和式（5）可以模拟樽海鞘链的行为机制。

3 混沌精英质心拉伸机制的樽海鞘群算法

3.1 改进Tent映射的种群初始化

樽海鞘群体的初始化对SSA 算法的收敛速度和寻优精度至关重要。在樽海鞘群初始时，由于没有任何先验知识可使用，基本上大部分群智能算法的初始位置都是随机生成。文献[17]提出初始种群均匀分布在搜索空间，对提高算法寻优有很大帮助。

混沌序列具有随机性、遍历性和规律性等特点，通过其产生的樽海鞘群体有较好的多样性。其基本思路是，通过映射关系在[0，1]区间产生混沌序列，然后再将其转化到个体的搜索空间。产生混沌序列的模型有许多，文献[18]提出，Tent 映射比 Logistic 映射能够生成更好的均匀序列。但Tent 映射产生的混沌序列存在小周期和不确定周期点等缺点。为克服此类缺陷，在原有的Tent混沌映射中加入一个随机变量r/N，改进后的Tent映射的数学表达式为：

其中，r为[0，1]之间的随机数；μ∈[0,2]是混沌参数，μ越大，混沌性越好，本文取μ=2；i=1,2,…,N表示种群规模；j=1,2,…,d表示混沌变量序号。

Tent 混沌映射对初始值的选取非常敏感，给式（6）选取d个具有微小差异的初始值，则可得到d个混沌序列。然后再将d个混沌序列进行逆映射，得到相应的个体搜索空间变量。

其中，[lbi,ubi]为的搜索范围。

3.2 精英质心拉伸机制

文献[16]提出重心反向学习策略，利用种群的重心生成反向解，以更好利用群体信息。虽然这样考虑到利用整个群体的信息，但包含的个体信息较多，算法运行成本较大。本文提出精英质心拉伸机制，选取群体中m个精英个体，求解其质心，然后根据质心对精英个体进行拉伸机制。质心和拉伸机制定义如下：

定义1（质心）设(x1,x2,…,xn)为D维搜索空间中n个个体，则其整体的质心定义为：

即得：

定义2（拉伸机制）若精英个体的质心为C，则某个精英个体xi的拉伸点定义为：

式中，w为[-1,1]之间的随机数，a为一个极小的正数，F为适应度函数，LS为拉伸因子，衡量精英个体与全局最优个体的差异程度，引导精英个体向质心个体学习。

由上述精英质心拉伸机制可以发现，利用精英个体的质心，作用于精英个体本身，以提升精英个体的性能。本文对当前种群中适应度最好的前m个精英个体运用拉伸机制。精英质心拉伸机制可从以下两方面增强算法性能：首先，将拉伸后新群体与当前群体融合，选出融合后一半的最优个体进入下一代种群中，以增强群体的多样性，可减小算法陷入局部最优的概率；其次，充分利用当前群体中精英个体搜索空间的有效信息，以此加快算法的收敛速度。由此可见，精英质心拉伸机制可较好平衡算法的探索和开发能力。

3.3 CESSA算法步骤

混沌精英质心拉伸机制的樽海鞘群算法步骤如下：

步骤1 初始化个体位置。使用改进的Tent 映射生成混沌序列，根据搜索空间的上下限，再把混沌序列逆映射为一个N×d维的矩阵。

步骤2 计算初始适应度值。根据测试函数计算N个樽海鞘的适应度值。

步骤3 选定食物源。把步骤2 中计算后的适应度值进行升序（或降序）排列，适应度值最好的樽海鞘位置选定为食物源位置。

步骤4 领导者和追随者位置更新。确定食物源位置之后，选取种群中一半的樽海鞘个体根据式（2）更新领导者位置，其余的樽海鞘根据式（5）更新追随者位置。

步骤5 精英质心拉伸机制。利用3.2节定义2所描述的精英质心拉伸的方法对当前种群中m个精英个体求解拉伸解，并比较更新每个樽海鞘个体的位置。

步骤6 计算适应值。计算更新后种群的适应度值，并更新食物源位置。

步骤7 重复步骤4～步骤6的更迭过程，如果达到设置的精度要求或规定的最大迭代次数，则终止算法，输出全局最优解。

4 仿真实验与结果分析

为验证本文提出的CESSA算法在求解优化问题上的有效性和鲁棒性，将CESSA 算法与SSA、PSO 以及GA 在12 个典型的标准测试函数最优值求解上独立进行50 次对比实验1。另外还在CEC2014 基准函数中选取部分函数进行对比实验2。

实验1 采用如表1 所示的12 个复杂函数作为适应度函数。选取的测试函数中包含单峰、多峰等不同特征的测试函数。单峰函数为在定义上下限内只有一个严格上的极大值（或极小值），通常用来检测算法收敛速度。多峰函数为含有多个局部最优解或全局最优解的函数，经常用于检测算法探索能力和开发能力。另外，测试函数的求解维度也是一个重要因素，算法对低维度求解质量好时对高维度不一定也好。表1 中测试函数维度从2维到200维，这可以更加全面地验证算法性能。

表1 基准函数

实验环境为：Windows7系统，8GB内存，CPU 2.5GHz，算法基于Matlab14b用M语言编写。

实验设置最大迭代次数为1 000，初始樽海鞘群、粒子群和染色个体的规模都为30。对于CESSA、SSA、PSO和GA算法的其他相关参数设置如表2所示。

表2 算法参数设置

表3 记录了50 次独立实验后从每种算法获得结果的最佳值（Best）、平均值（Mean）和标准偏差（Std）以及求解成功率（Successful Rate，SR）和平均耗时（Time）等多个实验对比数据。其中求解成功率为计算成功次数除以本次实验的求解次数。判断一次求解是否成功按照下式：

式中，FA为每次实际求解最佳值，FT为测试函数理论最佳值。

首先，表3 中的最优值、平均值都可以反映算法的收敛精度和寻优能力。对于6 个单峰函数(f1～f6) ，CESSA算法在求解精度上最高达到1E-33。同时，随着搜索空间维度的增加，寻优收敛精度4 种算法都在下降。另外标准SSA 算法在求解f4的时候，SSA 算法的求解能力就很差，与理论最优值存在1E+03 级的误差。而 CESSA 相对于 SSA、PSO 和 GA 寻优精度都要好，并且其求解精度变化不大。伴随求解维度的增加，对于算法求解难度也呈指数级别递增，算法的收敛精度有所降低属于正常现象。对于6个多峰函数(f7～f12)，算法求解精度相对于单峰函数要低一些。同样，随着维度增加，算法求解精度也有所降低。当维度增加到200 维时，CESSA算法求解f12的精度降到1E-01，但CESSA算法较其他三种算法仍然具有很好的优势。因此，CESSA算法在求解单峰、多峰以及高维的基准函数时都有更好的寻优效果和鲁棒性。

表3 各算法基准函数的结果对比

其次，表3～表5中标准差和成功率可以反映算法的稳定性和跳出局部最优的能力。在f12函数的求解上，CESSA 算法的寻优结果和理论结果还存在精度不足，但CESSA算法独立50次计算的标准差基本比其他三种算法都要小。这说明CESSA算法对于低维和高维基准函数的寻优求解有着很好的稳定性，且在多峰函数上寻优能力比较强，跳出局部最优的能力相对于其他算法更好些。6个基准函数中有单峰、多峰、低维和高维，除了求解200 维成功率较差，CESSA 在成功率上基本为100%，而标准SSA在f1和f2这两个基准函数的成功率为100%以外，其余基准函数成功率全部为0。随着搜索维度的增加，标准SSA在寻优求解能力上表现着很大不足。特别是在求解多维函数时，标准差和成功率都较差，说明标准SSA 跳出局部最优的能力是较弱。而在CESSA 中引入精英质心拉伸机制后，这对算法后期跳出局部搜索具有很大作用。

再次，从平均耗时来看。由表3可知，改进的CESSA算法相对于标准SSA的平均耗时都要大，PSO算法和标准SSA算法互有优劣，但总体运行时间均要优于CESSA算法和GA 算法。CESSA 算法在SSA 种群更新后引入精英质心拉伸算子，使得算法能够搜索到更多的解，这也就增加了算法运行时间。总体来看，CESSA 平均耗时比另外两种算法增加得并不是很大，在允许范围内。

Derrac 等在文献[19]中提出，对于改进进化算法性能的评估，应该进行统计检验。换而言之，仅基于平均值和标准偏差值来比较算法优劣还不够，需要进行统计检验以证明所提出的改进算法比其他现有算法具有显著的改进优势。为了判断CESSA的每次结果是否统计上显著地与其他算法的最佳结果不同，Wilcoxon 秩和检验在5%的显著性水平下进行。表4给出所有基准函数的最优值和其他算法的Wilcoxon 秩和检验中计算的p-value。例如，如果最佳算法是CESSA，则只在CESSA/SSA，CESSA/PSO、CESSA/GA 等之间进行成对比较。由于最佳算法无法与自身进行比较，针对每个函数中的最佳算法标记为N/A，表示“不适用”。这意味着相应的算法可以在秩和检验中没有统计数据与自身进行比较。根据Derrac等人的论文，那些p-value<0.05的可以被认为是拒绝零假设的有力验证。

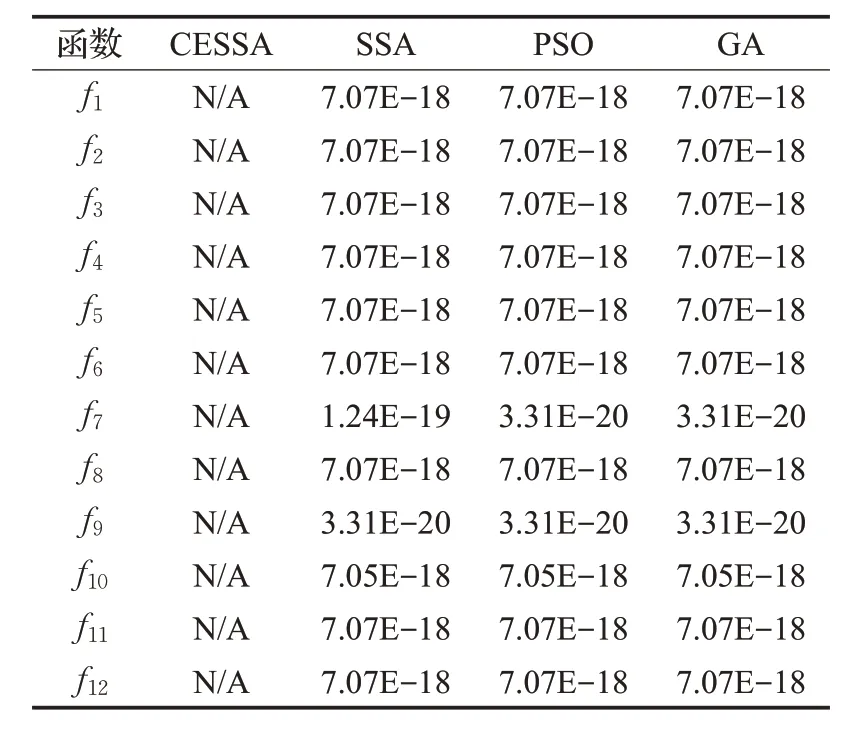
表4 Wilcoxon秩和检验的p-value

根据表4 中的结果，CESSA 算法的p-value全部小于0.05，这表明该算法的优越性在统计上是显著的，即认为CESSA算法比SSA、PSO、GA具有更高的收敛精度。

所有算法的定量分析是基于12个基准函数的平均绝对误差（Mean Absolute Error，MAE）。文献[20]提出对优化算法进行排序，MAE 是一种有效且可行的性能指标。表5 给出了这些基准函数的MAE 排序，其计算公式如下：

式中，mi为算法产生的最优结果的平均值，oi为相应基准函数的理论最优值，Nf为基准函数个数。计算出的MAE在表5中给出。

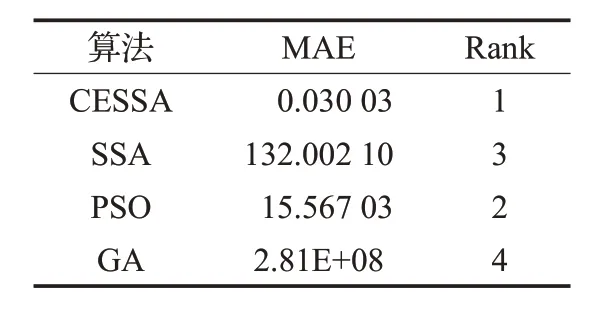
表5 MAE算法排名

由表5 可知，CESSA 排名为1，与另外三种算法相比，CESSA 提供了最小的MAE，进一步说明了CESSA的有效性。

图1给出4个基准函数的平均收敛曲线。由于不同算法收敛精度存在较大差异，为便于观察收敛情况，本文对寻优适应度值（纵坐标）取10 为底的对数。由图1（a）、（b）可看出，CESSA 算法的收敛曲线下降较快，并随着更迭次数的增加持续寻优，只在后期出现停滞。从图1（a）、（b）可知，GA、PSO和SSA在迭代后期出现不同程度的停滞，且寻优精度较低。图1（c）、（d）是多峰函数的平均收敛曲线。从CESSA 算法的收敛性上可以看出，在f11上迭代前期收敛速度比较平缓，后期收敛速度较快。在f8函数上，CESSA算法在前期收敛速度较快，但算法前期收敛速度相对于PSO较慢。CESSA后期出现一定程度停滞，但收敛精度比另外三种算法要好。从图中还可以看出，SSA、PSO和GA在后期基本都陷入局部最优，但CESSA 算法最终的寻优精度较其他算法仍然表现较好。无论单峰、多峰，还是低维和高维，对于每个基准函数CESSA比其他算法的收敛速度和寻优精度要好。

图1 部分基准函数平均收敛曲线

实验2 为更好评估CESSA 算法的有效性和稳定性。本文还在CEC2014 基准函数中选取部分单峰、多峰、混合（Hybrid）和复合（Composition）类型的函数进行优化求解，如表6所示。在该实验中，种群规模为30，最大迭代次数为500，维度为30。

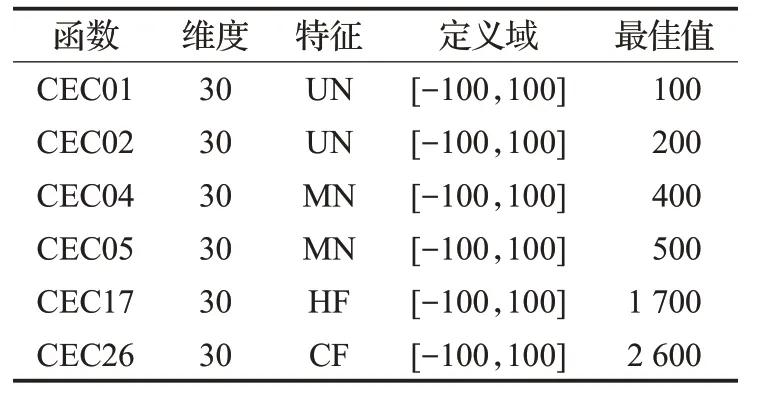
表6 CEC2014基准函数

表7 记录了CEC2014 中部分函数独立运行30 次后每种算法的平均值和标准差的结果对比。CEC2014 函数具有复杂的特征，因此所有算法都较难找到函数最优值。表7中结果显示，CESSA算法在6个CEC2014基准函数上都求得比其他三种算法更优的结果，进一步验证了CESSA算法具有较好的有效性和鲁棒性。

为比较本文改进算法与其他改进算法的优劣性，将CESSA 算法与参考文献[8]和文献[10]中改进算法进行比较，其中直接引用了文献[10]中CSSA1的数据，如表8所示（“—”表示参考文献中未给出）。表1 基准测试函数中可变维度函数的dim 都设置为10，种群数目为50，最大迭代次数为500。

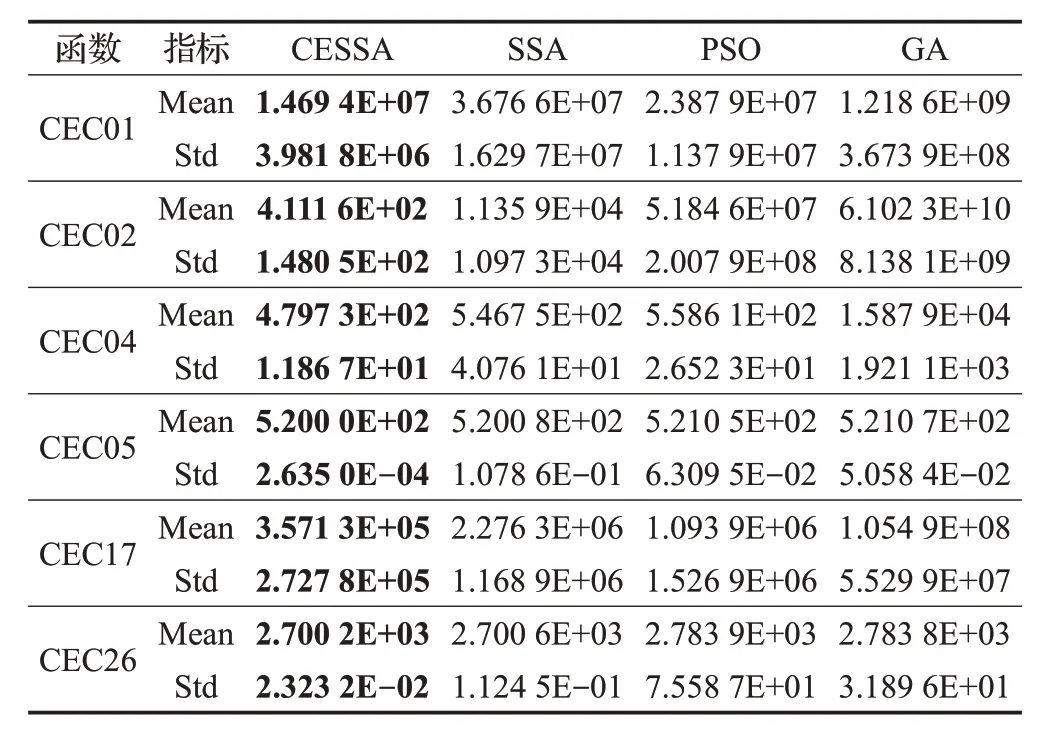
表7 CEC2014优化结果对比

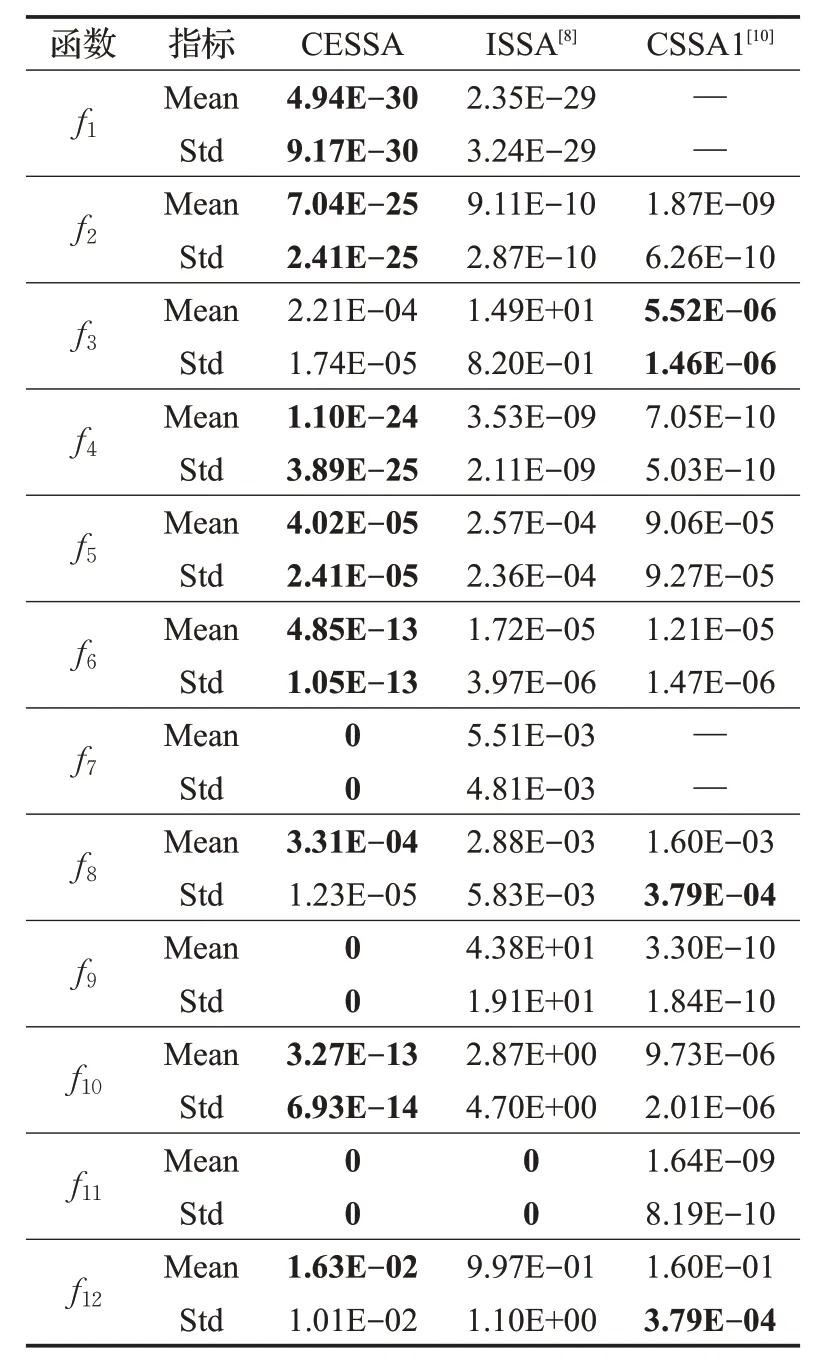
表8 与参考文献中算法性能的对比

由表 8 可知，除了在求解f3、f8、f12时，文献[10]算法的标准差好于CESSA算法，本文提出的CESSA算法在求解其他函数时的平均值和标准差都要好于文献[8]和文献[10]改进算法，进一步验证了CESSA 算法的有效性。

综上可知，混沌精英质心拉伸机制的樽海鞘群算法对本文所选取的基准函数都有很好的寻优结果，特别是对于高维、多峰的函数，具有较好的稳定性和寻优能力。

5 结束语

本文在标准樽海鞘群算法的基础上，引入改进的混沌映射和精英质心拉伸机制，提出一种改进的混沌精英质心拉伸机制的樽海鞘群算法，并将樽海鞘群算法应用于经典测试函数和CEC2014函数的寻优问题中。本文不仅使用最优值、标准差等指标对算法进行检验，还提出使用Wilcoxon 秩和检验对算法显著性水平进行验证。研究表明：基于混沌精英质心拉伸机制的樽海鞘群算法可以获得更好的全局搜索和局部搜索能力，且可以收敛到质量更好的最优解，算法的有效性和鲁棒性也得到验证。