干扰约束下集装箱码头全岸线岸桥调度研究

梁承姬，余 健

上海海事大学 物流科学与工程研究院，上海 201306

1 引言

近十年以来，全球集装箱量增长迅速。2017年国内规模以上港口集装箱吞吐量增速为8.3%，外贸集装箱规模增长为2.37 亿TEU。随着集装箱贸易量的不断增长，自动化码头成为未来发展的一大趋势，而传统码头的改造又是发展自动化码头的重要组成部分，在这一过程中码头资源的合理利用显得尤为重要。岸桥作为连接船舶与岸线作业的重要码头资源，如何高效合理地利用岸桥，对整个码头作业有着较大的影响。岸桥资源计划分为岸桥分配计划（Quay Crane Allocation Problem，QCAP）和岸桥调度计划（Quay Crane Scheduling Problem，QCSP），而岸桥的分配与调度问题（Quay Crane Allocation and Scheduling Problem，QCASP）是对前两者的综合考虑，在已知船舶岸桥服务数量前提下，对岸桥进行作业任务顺序的优化，使得在满足相关约束的条件下，实现岸桥的完工时间最短的目标。

针对岸桥调度问题，Kim等[1]在其模型中，通过考虑相邻贝位间任务的非同时性约束，来确定岸桥间的安全距离，同时提出了分支定界算法进行求解，并将计算结果与贪婪随机自适应性搜索算法进行比较，得出分支定界法比贪婪随机自适应性搜索算法性能要好，其缺点是无法解决较大规模的问题。Bierwirth等[2]在充分考虑岸桥干扰因素的限制下，建立了改进的岸桥配置与调度模型，同时提出了一种以分支定界法为核心的启发式算法，计算得出了更优的解。Chung 等[3]设计了一种改进的遗传算法，应用于岸桥调度问题，并与其他算法对比得出，该算法的性能更优。丁玲等[4]针对岸桥调度问题的特性，在模型中增加了任务的优先关系约束，并提出一种启发式算法，结果表明该模型和算法在一定时间内能得到较优的可行解。Diabat 等[5]在考虑岸桥初始作业位置的前提下，设计了一种改进的自适应遗传算法（Genetic Algorithm，GA），并通过与建立的数学模型计算结果对比，得出算法性能的优越性。Kaveshgar等[6]在传统岸桥调度问题（QCSP）的基础上，考虑岸桥作业的时间可用性，提出了带有时间窗的岸桥调度问题，并设计了一种特殊的遗传算法进行求解，通过对比，该算法性能更优，所得到的解质量更高。Al-Dhaheri 等[7]在调度方案中考虑了多个贝位间的任务均衡性，使得最终的调度方案更具有现实意义。Al-Dhaheri等[8]以船舶稳定性为基础，考虑岸桥作业的冲突与移动约束，建立新的MIP模型，同时设计改进的遗传算法进行求解。Lee 等[9]考虑岸桥调度问题中的岸桥双循环问题，建立了一种双机流水车间计划模型，并通过约翰逊规则进行求解。Zhang 等[10]为岸桥调度问题设计了一种基于分区的算法，并考虑多个岸桥处理速度的不同，为岸桥划分了相应的任务区间，以达到岸桥总体作业时间最小的目标。Ochoa-Zezzatti 等[11]针对QCSP 问题的算法求解进行了改进，设计了贪婪搜索以及蚁群相结合的启发式算法，并通过算例验证了改进算法的有效性。Diabat等[12]将泊位分配与QCSP问题相结合，建立了一种包含多种实际约束的数学模型，该模型更具有实用性。Al-Dhaheri[13]将船舶的稳定性引入QCSP问题中，并建立相应模型及算法，最终得出了岸桥在单贝位内的作业顺序。

以上研究大多将岸桥调度与实际贝位任务量分开考虑，而涉及贝位间任务均衡的研究中，岸桥的干扰约束、作业冲突等未被充分考虑。为此，本文将从贝位任务量的角度出发，以贝位为单位将整个岸线划分为若干区域，针对贝位任务量的动态变化，研究全岸线的多目标岸桥动态调度问题，即要求最小化岸桥最大完工时间的同时，缩短岸桥作业过程中的等待时间与移动时间，最终达到全岸线上岸桥的相互支援，从而得到最佳的岸桥调度方案。

2 问题描述

在全岸线岸桥动态调度问题中，本文从整体出发，将岸线长度和船长以贝位为基础，划分为若干个单位（不足一个贝位的按照一个贝位计算），并在此基础上进行岸桥的配置与调度研究。图1（a）为岸桥调度的初始方案，4个（台）岸桥服务两艘船舶，随着任务的进行，岸桥在贝位间移动，以完成全部任务，此时岸桥作业顺序的不同，会影响总体完工时间。

由于岸桥固定在轨道上，岸桥在作业过程中需考虑干扰因素，其主要为：（1）不可交叉因素，即岸桥不可跨越作业；（2）安全距离因素，即相邻岸桥间必须保持一定安全距离。由于这些干扰因素的存在，岸桥在作业过程中会产生等待时间，也会影响岸桥总体的完工时间。图1（b）为岸桥作业过程中存在等待时间的示意图，QC2在完成Bj+2任务后需移动到Bj+1位置，移动时间为T(j+2)(j+1)，因为安全距离约束（安全距离为2个贝位）及不可交叉约束的存在，QC2 需等待时间为TW，使得整个完工时间延后。

本文提出了一种基于滚动计划的全岸线岸桥的动态调度方法，以保证在决策周期内岸桥等待时间以及移动时间最小的前提下，最小化岸桥的最大完工时间。

图1 岸桥调度示意图

3 模型建立

本文考虑的是全岸线QCSP问题，将整个岸线划分成若干贝位，不同类型的船舶靠泊时仅考虑所占岸线贝位数量，在船舶靠泊位置及时间已知的前提下，对全岸线岸桥进行动态调度。

3.1 模型假设

（1）岸桥被固定在同一轨道上，不可交叉，即不可跨越作业。

（2）相邻的两个岸桥间存在V个贝位的安全距离，即相邻V个贝位距离内不能同时作业。

（3）两个岸桥不能在同一时刻处理同一贝位的任务。

（4）岸桥的初始作业时刻已知。

（5）岸桥移动速度恒定，且岸桥的作业效率相同。

（6）岸桥处理每个贝位的任务时间为整数时间单位，即任务量由整数时间单位表示，单位为h。

（7）岸桥的初始位置已知。

（8）每个贝位的任务由不同岸桥在不同时刻处理完成。

3.2 集合、参数及决策变量的定义

集合、参数定义：B表示贝位集合，贝位从左到右依次编号为{1,2,…,i},i,j为贝位编号索引，i,j∈B；Q表示岸桥集合，{1,2,…,k}为岸桥编号，k∈B,岸桥编号方式与贝位编号方式一致；Pi为岸桥处理任务i的时间；li表示贝位i存在任务需要处理；表示岸桥k的初始位置；表示岸桥k在完成分配任务后的终止贝位；rk表示岸桥k开始处理任务的时间；θ表示岸桥在两个相邻贝位间的单位移动时间，即岸桥k从任务贝位i移动到任务贝位j所用时间为表示岸桥从初始贝位移动到第一个任务贝位j的时间，表示岸桥k完成最后一个任务贝位j后，移动到终止位置所耗费时间，理论上为0，=；V表示相邻岸桥k和岸桥k+1 之间的安全距离，通常为1 个贝位；M表示足够大的整数；α1表示任务最大完工时间分配的权重；α2表示分配给岸桥在岸线上移动时间的权重；α3表示分配给岸桥等待作业的时间的权重。

3.3 目标函数及约束条件

岸桥装卸作业存在相互协调的问题，本文在各目标间设置相应的权重进行调整。

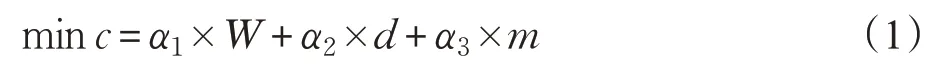
约束条件为：

式（1）表示最小化岸桥最大完工时间的同时，缩短岸桥的移动时间和等待时间；式（2）表示岸桥任务的最大完工时间为W；式（3）表示单个任务只能由一台岸桥完成；式（4）和（5）分别说明每个岸桥的初始任务和最终任务有且只有一个；式（6）定义了任务的优先级，即任务i要先于任务j处理；式（7）表示任务j的完成时间，比任务i的完成时间加上任务j的处理时间以及岸桥在贝位i、j的移动时间要大；式（8）说明由于冲突的存在，部分任务无法同时处理；式（9）定义了岸桥作业时不能产生干涉；式（10）说明任务j的完成时间，比任务i的完成时间加上任务j的处理时间要大；式（11）表示岸桥的初始任务完成时间大于岸桥从初始位置移动到任务贝位的时间加上初始任务的处理时间；式（12）表示岸桥的最终完成时间等于最终任务的完成时间加上从该位置移动到最终位置的时间；式（13）定义了岸桥在岸线上总的移动时间；式（14）表示岸桥总的等待时间为岸桥完工时间、岸桥移动时间以及任务处理时间的差值；式（15）和（16）定义了yik和的关系；式（17）说明了岸桥处理任务存在天然的顺序要求；式（18）定义了W、m、d三者的权重关系；式（19）确定岸桥在依次作业过程中，相邻岸桥间保持V个贝位的安全距离；式（20）和（21）确保了决策变量为0-1变量以及模型中的变量均大于0。

4 算法与规则设计

考虑到问题的复杂程度，本文采用遗传算法进行求解，并结合Meisel 等[14]提出的算法求解方案，对遗传算法所求解的结果进行了优化。

4.1 染色体编码

本文采用矩阵式编码，染色体的每一行代表分配给一台QC要处理的任务数，染色体每一列代表一个贝位，因此染色体长度与船舶贝位数相等，染色体的基因值表示QCi处理贝位Bj的任务量，0 表示没有可处理的任务；染色体第j列基因值的和与该贝位需要处理的任务数相等，第i行的和与分配给该岸桥的总任务数相等。图2为有3台岸桥、10个贝位的染色体编码。

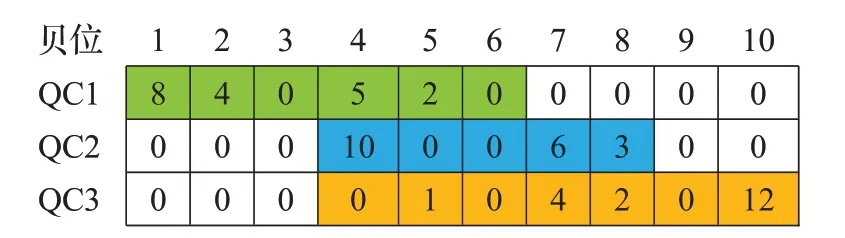
图2 染色体示例

4.2 适应度函数与选择策略

适应度函数为fitness=1/(minc)，即岸桥最大完工时间、岸桥移动时间和岸桥等待时间的和最小化的倒数。此处使用的染色体仅指定QC到贝位的分配。在评估其适应性之前，必须将一个时间表与染色体关联起来，以计算适应度值，本文采用50%的精英保留策略，在种群中选择具有最高适应值的染色体直接保留至下一代，从而保证算法的全局收敛。

通过GA 中的目标函数（适应度函数）确定每个岸桥的初始位置、每个任务的起始和结束时间以及每个岸桥工作的位置，并存储在矩阵数据结构中。每次岸桥需要开始处理与岸桥当前贝位不同的贝位的新任务时，它将检查相邻贝位（在新任务贝位的左侧和右侧）的任务是否有其他岸桥占用。如果因为不同岸桥执行任务干扰其移动，则检查这些任务的完成时间。如果这些任务没有完成，那么目前的岸桥需要等待；否则，它可以继续移动到下一个任务的贝位并开始卸载或装载作业。

根据岸桥的当前贝位，可将下一目标贝位与其他岸桥所在贝位，区分为以下四种干扰情况：

（1）岸桥前往其分配的任务并处理该任务；

（2）岸桥需要等待，以避免与另一台岸桥发生碰撞，然后运行到其下一个任务位置；

（3）岸桥保持闲置状态，并将停留在当前位置；

（4）岸桥保持闲置状态，但需要移动以避免与相邻的岸桥发生碰撞。

4.3 交叉与变异

因为染色体设计的特殊性，本文采用染色体基因值对应比例的组合交叉策略，并参考Tavakkoli-Moghaddam等[15]在2009 年提出的改进遗传算法中的交叉策略，具体操作如下：

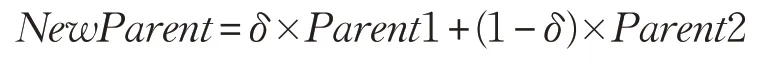
其中δ是在（0.5，1.0）之间随机生成的常数，表示父代1拥有更好的适应性，在计算过程中采取四舍五入的方式保留基因值。图3所示为δ=0.6 的操作过程。

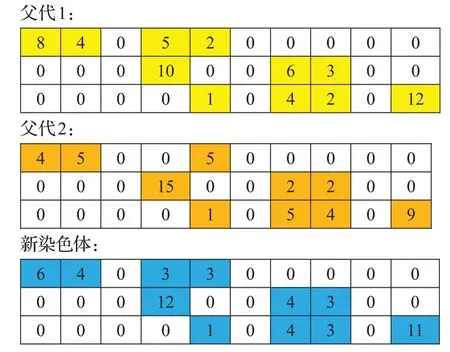
图3 交叉

变异则是采取交换变异的方式，随机选择第i行的两个基因值，最小的基因值与对应的第i+1 行的基因值交换位置，最大的基因值与对应的第i-1 行的基因值交换位置；若所选行为首行或末行，则在此两者相互为最大值与最小值对应基因位互换。图4为变异操作过程。

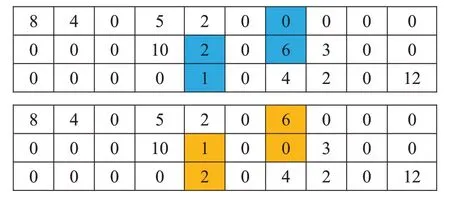
图4 变异

4.4 结束规则

按照改进的算法步骤，以适应度函数为衡量标准，在初始种群的基础上产生新的种群，从而保证种群的多样性，在算法达到最大迭代次数时，算法将终止迭代。

5 算例与结果分析

为了验证本文所提出的模型及算法的可行性，设计了不同情形及规模的算例。岸桥开始作业时刻在不同算例中不同，相邻岸桥间存在1 个贝位的安全距离，同时岸桥在相邻贝位间的移动时间固定为1 个时间单位。模型中设定的目标函数权重分别为α1=0.6，α2=0.2，α3=0.2。

遗传算法的参数为交叉概率0.9，变异概率0.2，种群大小为150，最大迭代数为300。实验在Intel®CoreTMi5 的处理器、内存 4 GB 的 PC 上进行，采用 Matlab2018a编程实现。

5.1 小规模算例

岸线作业区域为10 个贝位，岸桥数为3，每个贝位的任务量如表1所示。分别计算遗传算法与Cplex的结果，并进行比较，如表2所示。

表1 贝位任务数

表2 遗传算法与Cplex求解结果对比

由上述对比结果可知，两者的求解结果一致，但Cplex的计算时间要更短。调度方案如图5，遗传算法的收敛结果如图6。由算法收敛图可知，大约在140 代得到最终收敛结果，避免了前期的局部最优解。最终方案中岸桥1的作业路径为4-2-1；岸桥2的作业路径为7-5-4；岸桥3的作业路径为10-8-7。岸桥最大完工时间为24，船舶1的完工时间为22个时间单位，船舶2的完工时间为24 个时间单位，在整个作业过程中岸桥的等待时间为0，岸桥1、岸桥2和岸桥3的移动时间都是3个单位。

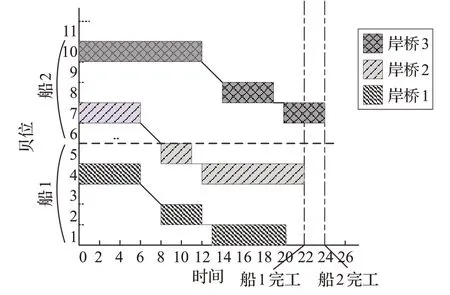
图5 调度方案示意图

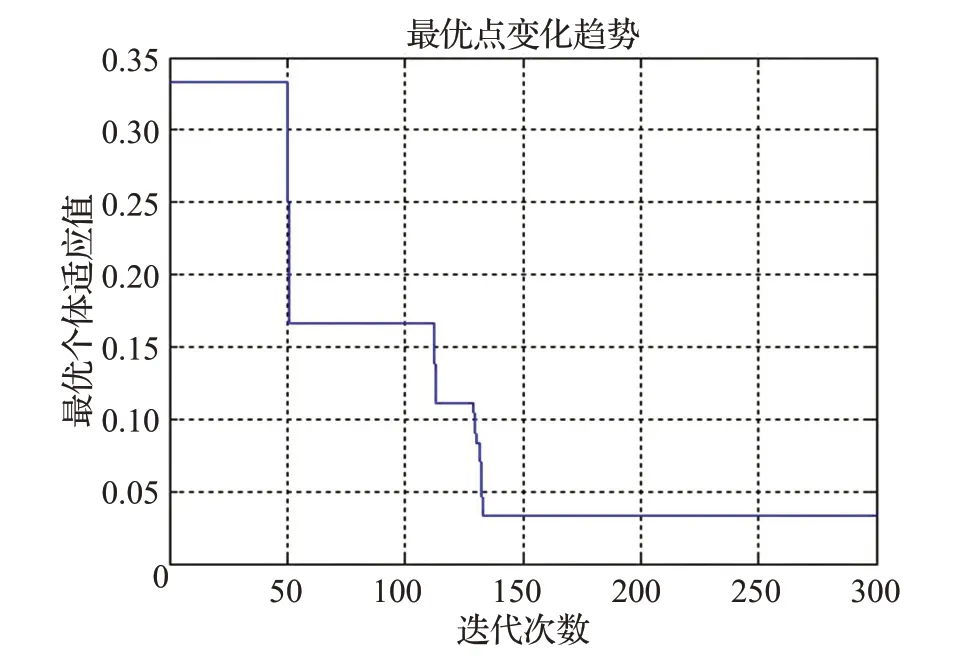
图6 算法收敛图

5.2 大规模算例

岸线长为40个贝位，岸桥数为10台，表3所示为每个贝位的任务数，表4为船舶计划，计算结果见表5。

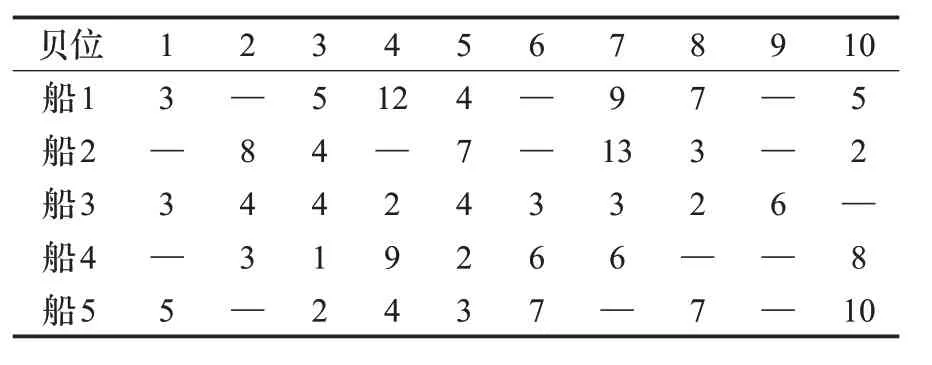
表3 贝位任务数

表4 船舶计划

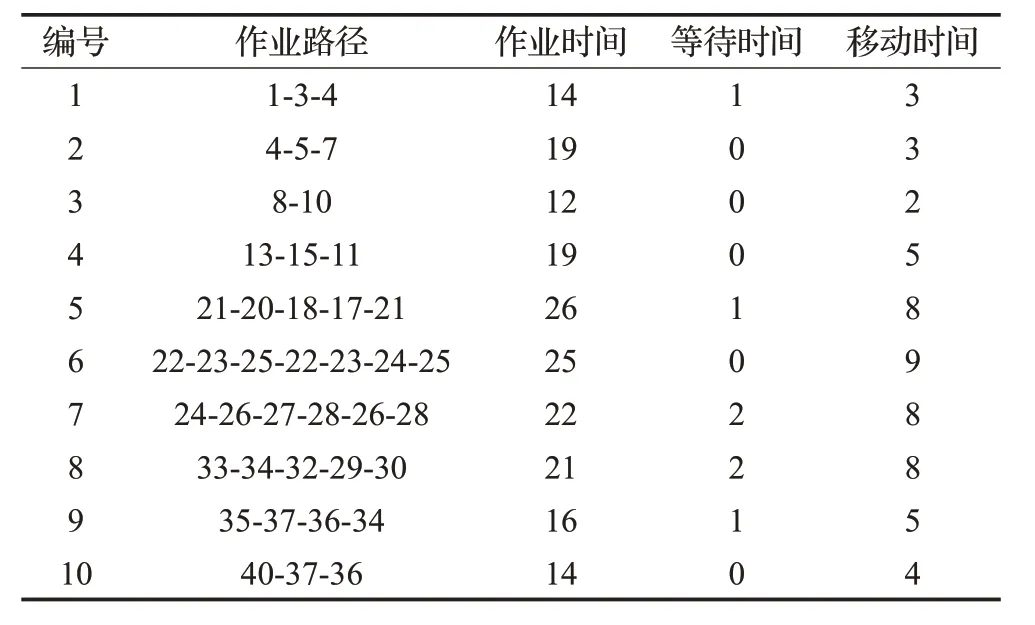
表5 岸桥作业路径及时间

在大规模算例计算中，依据遗传算法的结果得到调度方案如图7。最终方案中船舶1的完工时间为22个时间单位，船舶2 的完工时间为24 个时间单位，船舶3 的完工时间为18 个时间单位，船舶4 的完工时间为21 个时间单位，船舶5 的完工时间为16 个时间单位，在整个作业过程中岸桥的等待时间为7个时间单位。

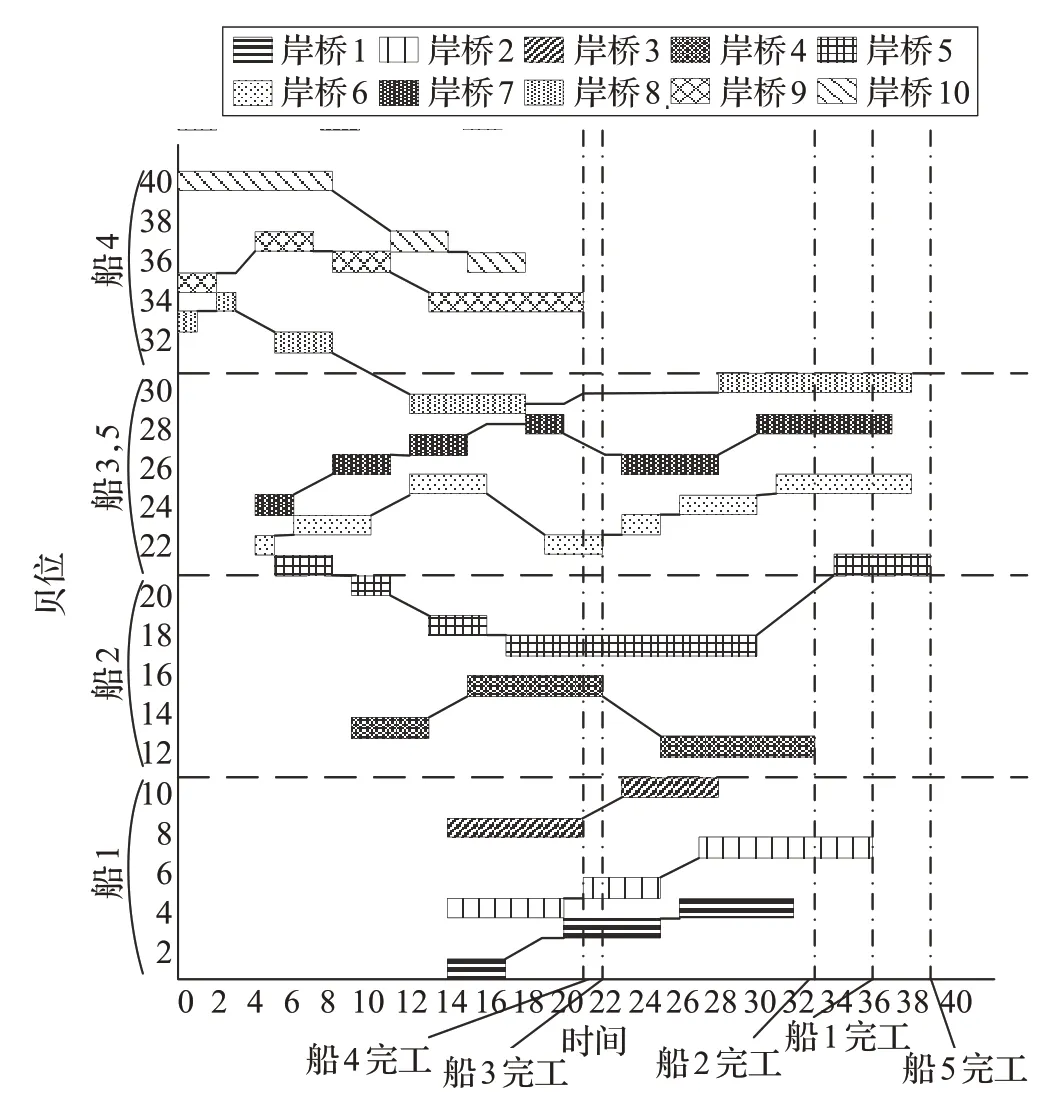
图7 调度方案示意图

表5 为岸桥的作业路径及完工时间表。由表可知岸桥的最大作业时间为26 个单位时间，主要原因为两艘船舶先后靠泊在20～30 贝位的位置，导致任务量增加；移动时间受到任务贝位数影响，呈现明显的正相关趋势；等待时间均处于较低水平。

表6 为全岸线调度与传统调度方案的结果对比。与传统方案对比，相同规模的算例下，传统调度的总完工时间要多于全岸线调度的总完工时间。由图8可知，随着算例规模的扩大，全岸线调度方案的优越性越明显，同时全岸线调度能够在规定周期内对船舶进行完工作业。

表6 全岸线调度与传统调度对比

图8 不同调度方式完工时间比较图

6 结束语

本文对集装箱港口的全岸线岸桥调度问题进行了研究，考虑到岸桥作业过程中的安全距离、不可交叉等约束，以减少岸桥的等待时间、移动时间以及最小化岸桥最大完工时间为目标，建立了混合整数规划模型，同时设计了改进的遗传算法进行求解。结果表明，该模型可以有效解决岸桥的分配与调度问题，并且随着问题规模的扩大，算法的优越性越明显。通过算例验证了本文研究可以为全岸线岸桥的调度方案提供科学合理的决策依据。另外，由于岸桥装卸时间受AGV调度的影响，后续将考虑在贝位任务量的基础上，进行全岸线岸桥与AGV的联合调度研究。