一种不规则形状聚类算法

2016-01-12谢梦燕,黄旭,赵青等

西安文理学院学报（自然科学版） 2015年3期

关键词：并行算法机器学习数据分析

一种不规则形状聚类算法

谢梦燕，黄旭，赵青，王俊辉

(湖州师范学院信息工程学院，浙江湖州 313000)

摘要：数据量的增长、数据复杂性日益突出对数据分析提出了更高的挑战.针对不规则形状分布的大规模数据，基于数据的本质特征对简单聚类策略进行研究，同时对采用并行方法提高分析效率进行了思考.模拟实验表明，这种方法能够有效识别复杂分布的类别边界.

关键词：聚类；不规则形状；机器学习；数据分析;并行算法;共享信息素矩阵

中图分类号：TP311文献标志码：A

文章编号：1008-5564(2015)03-0009-06

收稿日期：2015-02-10

作者简介：谢鸣凤(1990—)，女，安徽宿州人，南京航空航天大学理学院数学系硕士研究生，主要从事偏微分方程研究.

A Clustering Algorithm for Irregular Distribution

XIE Meng-yan, HUANG Xu, ZHAO Qing, WANG Jun-hui

(School of Information Engineering, Huzhou Teachers College, Huzhou 313000, China)

Abstract：The growing prominence of data growth and data complexity propose more challenges for data analysis techniques. For the irregular distribution of large-scale data, study on a simple clustering strategy was carried out based on the essential characteristics of data, and thoughts on improving the efficiency of data analysis was conducted by using the parallel method in this paper. The simulation test results show that this approach can effectively identify category boundary of complex distributions.

Key words：clustering; irregular distribution； machine learning； data analysis; parallel algorithm; shared pheromone matrix

聚类是机器学习领域一项重要的基础技术，是典型的无监督学习方法，它能够在目标数据对象中发现令人感兴趣的数据分布模式.聚类分析的算法可以分为划分法(Partitioning Methods)[1-2]、层次法(Hierarchical Methods)、基于密度的方法(density-based methods)[3-4]、基于网格的方法(grid-based methods)[5]、基于模型的方法(Model-Based Methods)等等.目前已广泛应用于基因、蛋白质等生物数据分析[6]，以及社会计算[7-8]、神经解剖学分析、卫星遥感影像分析、多传感器数据融合等诸多领域.

聚类方法通过对目标数据进行深入分析，试图挖掘出目标数据集合的分布规律，并基于此规律整理数据.而实际的数据集合分布往往具有复杂的子类边界，聚类算法通过简化边界的数学描述来提供一种聚类结果.这些简化的数学描述往往包含用来描述聚类半径、密度的相关参数等等.由于聚类分析的复杂性，聚类算法需要在算法执行速度以及类边界描述与实际类边界的拟合程度之间作出权衡.然而，对于一些分布规律极为复杂的数据集合，即使是在损失效率的前提下也很难获得良好的聚类效果.

1不规则形状聚类

呈现不规则分布的复杂数据集存在一些典型问题[9]，在空间拓扑关系上，包括数据子集的分离、邻接、包含、覆盖等情况；在子集密度问题上，包含不同子集之间的密度差异、同一子集之间密度差异两种情况；在子集形态方面，又存在子集形状多样性与子集大小性等问题.对于这一类不规则形状的聚类问题，需从两个方面进行研究，一是子类的刻画参数，二是并行处理方法.

最简单的类的刻画参数是聚类半径，如常用于蛋白质结构聚类的QT算法[10].该算法基于简单的半径这一概念对子集进行划分，通过简化聚类过程提高执行速度.此外还有数据密度、元素间距离等参数.基于相邻元素距离的分析方法是识别复杂子类的基础.假设点xi是聚类Ck的成员，即：xi∈Ck.在这里用d表示距离函数，如果点xj与点xi之间的距离小于事先设定的阈值T，即d(xi,xj)

在实际数据集中，相同聚类的数据一般呈现不均匀分布，且体现为连续变化趋势.数据的不均匀增加了选择T的难度，而连续变化趋势则提供了解决的思路.为更准确地刻画子集，可将相邻点的距离阈值用函数进行描述.最简单的描述方式是阈值变化函数：δ(Tn,Tm).其中Tm、Tn是在远离聚类中心的方向上相邻元素间的距离.δ是连续函数.那么判断相邻的两个数据点xk、xj是否属于同一子集可采用以下式子：d(xj,xk)<δ·d(xi,xj).其中xi、xj、xk是在远离聚类中心的方向上连续相邻的三个点.当上述式子不成立时，认为xk点处出现较大梯度，进而认为xk不适合与前两个点划为同一子类.

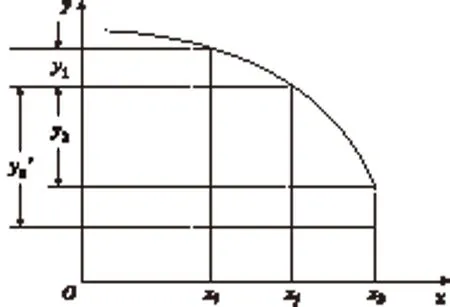
图1　基于相邻点距离的类归属分析示意图

更进一步，为刻画出δ的变化趋势可采用函数λ(δ).仍然以梯度作为判断一个点是否属于该类的条件.

如果用y统一上述不同的分析层次，则基于相邻点距离的类归属分析示意图如图1所示.

图中曲线为距离阈值函数，xi、xj、xk分别表示在远离聚类中心的方向上连续相邻的三个点，y1、y2、y2′是相邻距离分析值，根据采用的分析函数，可分别表示T、δ、λ等.如果xk点在规定的阈值范围内，即符合距离分析函数，则会出现在曲线上，与上一相邻点的距离为y2，否则不会出现在曲线上，与上一相邻点的距离为y2′.此处将呈现明显的梯度.

对于大规模数据，常采用并行算法提高聚类效率，目前采用MapReduce[11]方法成为一种趋势.在并行计算过程中，各并行体之间的信息交流是影响并行算法效率、需着重解决的问题.本文着重在共享全局类别归属信息的并行处理方法方面进行了思考.在并行聚类过程中，一方面，各并行体执行相同的操作，即从初始点出发，逐步分析相邻点的类别属性，试探着对相邻点进行类别划分.另一方面，各并行体通过共享全局类别归属信息对各自的分析行为进行指导.

2算法描述

以基于相邻元素距离的分析方法为例，不规则形状聚类算法基本思路是:随机选择聚类起点，并从当前处理类别开始标记类别序号；分别从各起点开始遍历所有点；将当前点xj与已处理过的点xi计算距离，对于距离小于给定阈值的情况，如果点xj无类别，则将该点标记为与xi的类别相同，否则，将与xi类别相同的所有点标记为点xj的类别；如果所有已处理过的点与xj的距离均大于阈值，则将xj设置为新类别.具体分析流程如图2所示.

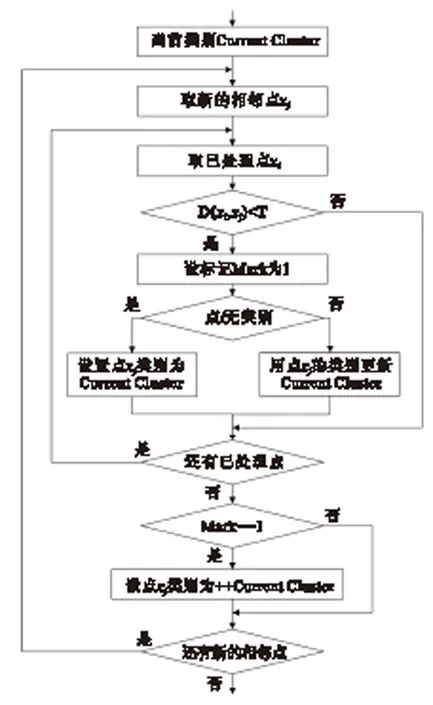
图2　数据分析流程

该流程反映了基于简单距离分析阈值T的情况.在该流程图中，d(xi,xj)

共享全局类别归属信息的并行处理方法的瓶颈在于类别信息的存储以及数据通讯.算法借鉴了采用共享信息素矩阵(Sharingonepheromonematrix,SHOP)策略蚁群算法的实现思路[12]，通过在内存设置共享区域来存储类别归属信息，数据通讯通过直接读写公共内存特定区域实现.并行机制如图3所示.

与SHOP不同，SHOP的信息素矩阵采用连续值对各蚁群行为进行指导，而本算法共享区域存储离散的类别归属，更易于实现.在该并行机制中，各并行体从随机起点开始执行，并通过全局类别归属矩阵交流各点的类别信息.如果在一定时间内所处理的各点类别信息均无改变，则认为达到全局收敛状态，退出并行体.

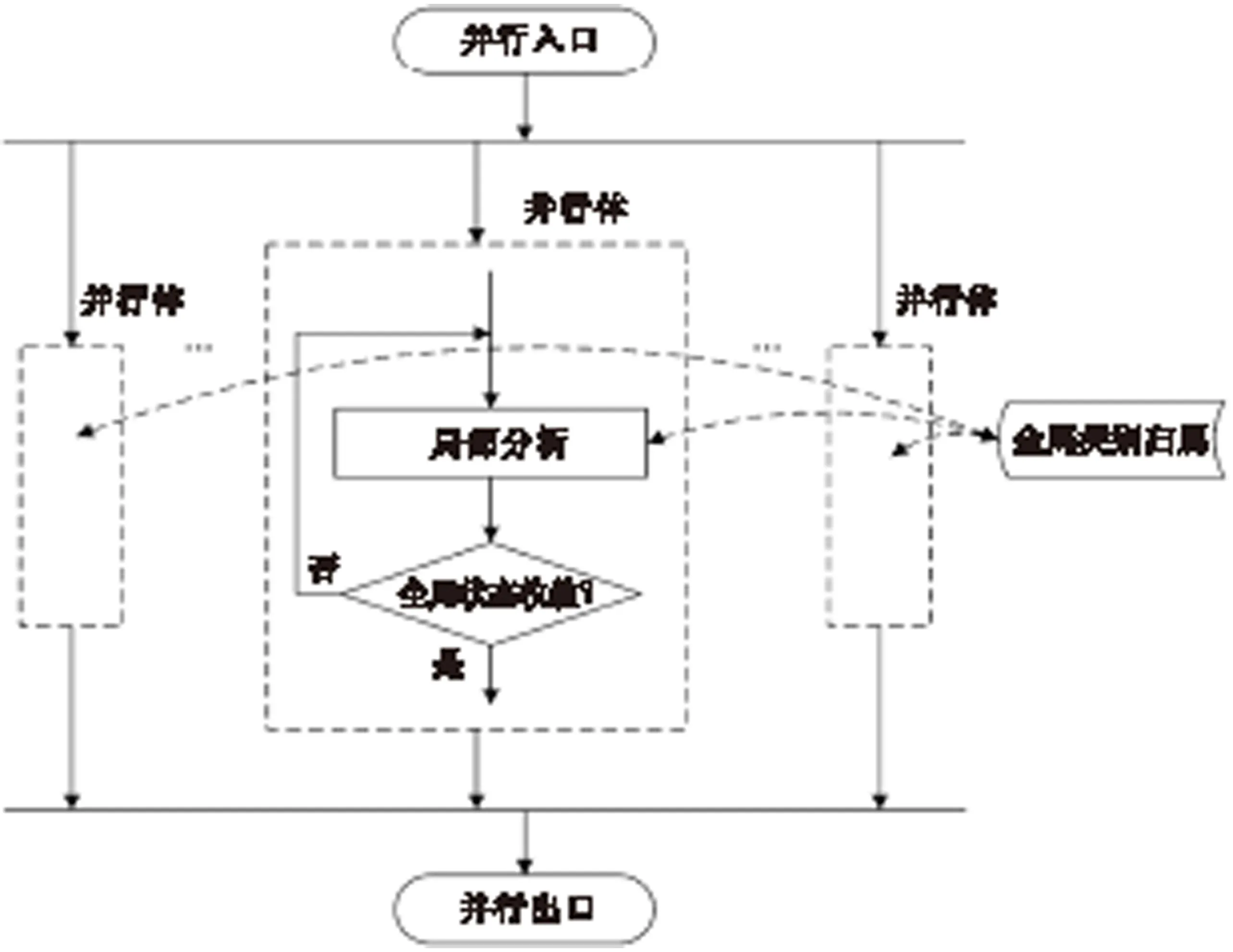
图3　并行机制

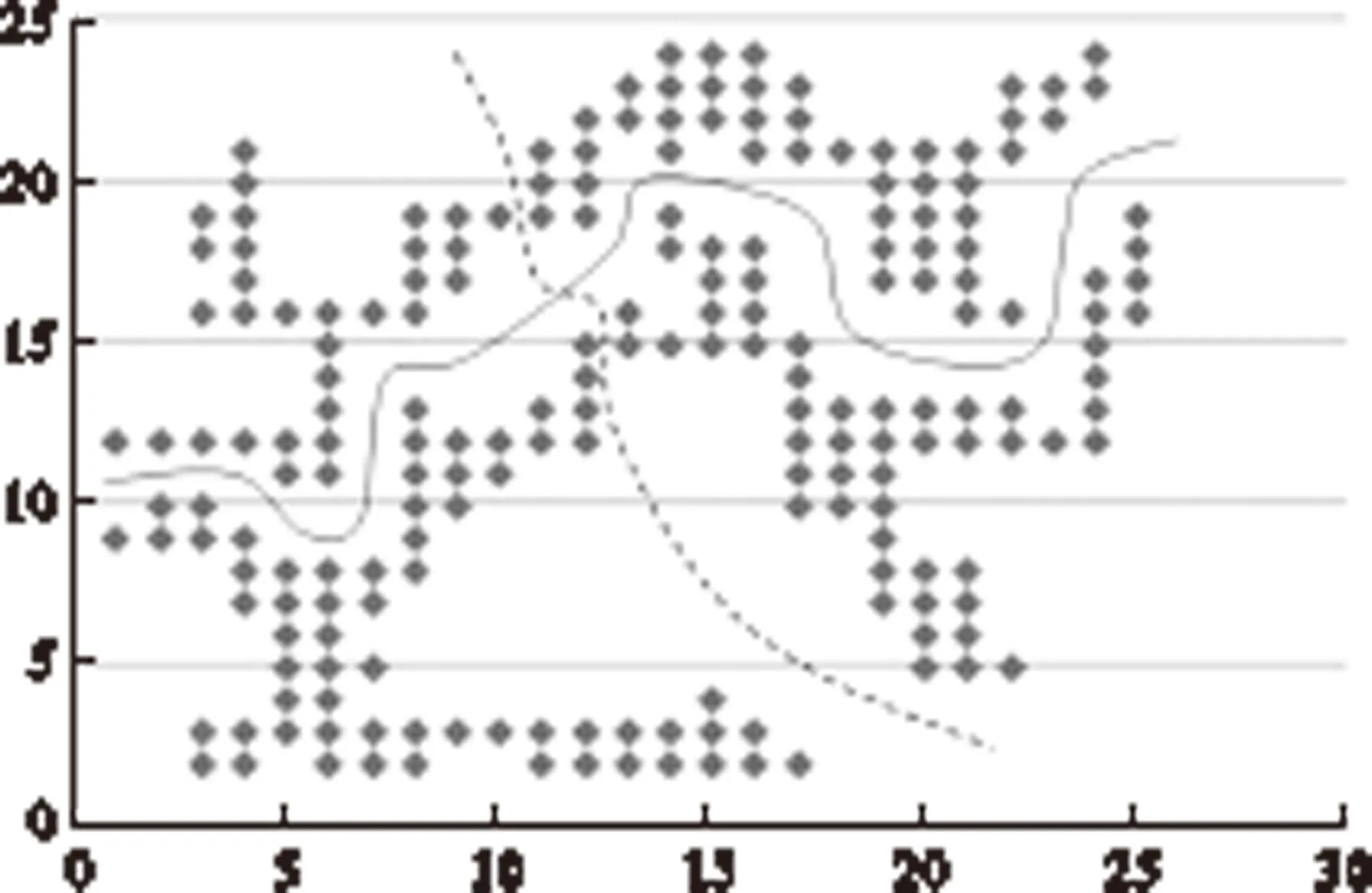
图4　聚类数据及结果

3实验与结果分析

本文用C++语言实现上述算法.实验在选定的二维数据集合上对算法进行验证，并与K-means聚类算法[5，13]进行比较.通过生成坐标方式产生二维数据集合，记录在文本文件中，每行记录一个点的信息，采用“编号、X坐标、Y坐标”的形式.为简单起见，数据坐标采用区间[0,30]中的整数，并通过调整坐标值使数据点呈不规则分布.假定数据点在坐标系中纵、横、斜向相邻为同一子类，有间隔为不同子类.然后在该数据集上分别运行本文算法和K-means算法.本文重在验证上述方案对呈不规则分布的复杂数据是否有效，只运行了单并行体.模拟数据在二维坐标系中的位置视图以及实验结果如图4所示.

图4中标注了两条曲线，其中实线为运行本文算法的聚类分界线，虚线为运行K-means算法的聚类分界线.本文算法子类间距离阈值取1.5，K-means算法初始类别数为2.实验结果表明，本文算法给出的结果更符合对模拟数据的聚类预期.通过实验，本文认为K-means算法倾向于聚集更为紧凑、形状更为规则的子集，即K-means算法对于聚集成团的聚类更有效，而本文算法对不规则形状聚类在子类边界的细节把握上更为准确.

4结语

数据量的飞速增长促使以聚类为代表的数据分析方法受到空前关注，而大规模数据的分布规律也越来越呈现出高度复杂性，大大增加了数据分析难度.对于不规则形状分布的大规模数据，本文基于数据的本质特征对简单聚类策略进行了分析，同时在并行方法方面进行了一些思考.在此基础上进行了模拟实验.实验表明，这种方法能够有效识别复杂分布的类别边界.下一步将深入研究数据边界的复杂刻画方法，尝试复杂距离分析函数在算法中的应用，同时进一步优化并行方案，提高聚类效率，并结合复杂数据的各类具体应用作进一步验证.

[参考文献]

[1]蒋亦樟,邓赵红,王骏,等.基于知识利用的迁移学习一般化增强模糊划分聚类算法[J].模式识别与人工智能,2013,26(10):975-984.

[2]殷君伟,陈建明,薛百里,等.一种基于排序划分的聚类初始化方法[J].微电子学与计算机,2013,30(6):80-83,87.

[3]武佳薇,李雄飞,孙涛,等.邻域平衡密度聚类算法[J].计算机研究与发展,2010,47(6):1044-1052.

[4]郑苗苗,吉根林.一种基于密度的分布式聚类算法[J].南京大学学报,2008,44(5):536-543.

[5]张真,任贺宇.一种基于动态网格技术的K‐means初始质心选取算法[J].微电子学与计算机,2013,30(6):101-104.

[6]高翠芳，吴小俊.复杂生物数据集的聚类数自动确定方法[J].生物信息学,2010,8(4):295-298.

[7]窦炳琳,李澍淞,张世永.基于结构的社会网络分析[J].计算机学报,2012,35(4):741-753.

[8]朱牧,孟凡荣,周勇.基于链接密度聚类的重叠社区发现算法[J].计算机研究与发展,2013,50(12):2520-2530.

[9]邓敏,刘启亮,李光强,等.空间聚类分析及应用[M].北京:科学出版社,2011.

[10]LAURIEJ.KRUGLYAKS,YOOSEPHS.Exploringexpressiondata:identiffcationandanalysisofcoexpressedgenes[J].GenomeResearch,1999,9:1106-1115.

[11]鲁伟明,杜晨阳,魏宝刚,等.基于MapReduce的分布式近邻传播聚类算法[J].计算机研究与发展,2012,49(8):1762-1772.