基于出射流速的反弧鼻坎挑距计算
2020-05-19李书芳吴建华
李书芳,吴建华,马 飞
(1.河北工程大学水利水电学院,河北 邯郸 056038; 2.河海大学水利水电学院,江苏 南京 210098)
在水利水电工程建设中,尤其高拱坝建设中,挑流消能因其经济可靠、结构简单,被工程中广泛采用[1-2]。其中水舌挑距是影响水垫塘设计及岸坡安全性的关键技术指标,在高坝建设的推动下,国内外学者在挑距研究方面取得了丰硕的成果。通常根据质点运动的抛射体理论计算水舌挑距[3]。当鼻坎结构选定时,挑距的影响因素有出射角[4-8]、出射流速[9-10]、空气阻力[11-12]、水舌掺气[13-14]、环境气压[15]等。由于水流受到反弧曲率的影响,水舌实际出射角并不完全等于鼻坎挑角,但是对高速水流情况下的反弧鼻坎,水舌出射角可近似用鼻坎挑角代替[16]。空气阻力和水舌掺气也是影响挑距的重要因素,当流速小于13 m/s时,水舌轨迹线为抛物线,但当流速大于40 m/s时,理论挑距比实测挑距减小30%以上[9]。同时,由于水舌挑射过程中分散掺气,水流运动轨迹与质点抛射体轨迹发生偏离。因此,刘宣烈等[11]提出了考虑空气阻力影响的水舌水平挑距计算式;刘士和等[13]在平面充分掺气散裂射流的数学模型的基础上,提出了考虑掺气及空气阻力影响的水舌挑距计算式。最近研究表明,环境气压也对水舌挑距产生影响,环境气压越低,挑距越远,环境气压每下降10 kPa,挑距增大约1.5%[15]。当水舌出射角用鼻坎挑角代替,且不考虑空气、掺气和气压的影响时,挑距的主要影响因素为出射流速。在DL/T 5166—2002《溢洪道设计规范》中,出射流速可按断面平均流速的1.1倍计。当泄槽较长时,可按水面线推算坎顶水深,进而求出断面平均流速,或者取流速系数,根据能量方程计算出射流速[16-17]。孙红娟等[18]结合实测挑距由抛物线公式反推得到出射流速的经验式,但由于实测挑距受前述诸因素影响,所得出射流速并非实际意义上的流速。
水舌上、下缘挑距范围决定了水垫塘的位置和尺寸,对于连续鼻坎,在高速水流情况下,水舌上、下缘出射角相差较小,可用鼻坎挑角代替,则影响挑距的主要因素为上、下缘出射流速的差异。尽管目前关于水舌挑距的研究已经相对成熟,但直接从水舌上、下缘出射流速的角度着手研究的尚不多见。本文通过理论分析,结合前人研究成果,从势流理论出发,探讨水舌上、下缘出射流速的计算方法,进而对反弧鼻坎水舌上、下缘挑距进行计算。
1 模型试验
模型试验在河海大学高速水流实验室进行,以某工程泄洪中孔为例,仅研究水平来流情况。试验布置平面图和实物照片分别如图1和图2所示。试验系统包括水泵、进水管道、平水塔、试验水箱、试验模型、量水堰和回水渠等。试验模型主体由有机玻璃制作,采用短有压进口,由进口段、有压段、明流渠段和鼻坎段组成。有压段出口设弧形闸门以控制来流水深,通过调整上游水位控制单宽流量。渠道底坡为0,鼻坎出口底板距下游底板高约65 cm,鼻坎反弧半径R=50 cm,挑角β=45°。试验单宽流量q如表1和表2所示。

图1 试验装置整体布置平面示意图(单位:cm)

图2 模型试验照片
2 反弧段流速分布
如图3所示,任取反弧段某断面建立正交坐标系,法线方向为y,切向方向为x,坐标原点O位于底板。在鼻坎反弧段,由于重力和离心力的共同作用,势流流速沿曲面方向(即x方向)和垂直于曲面的方向(即y方向)都有变化。研究反弧段任意断面流速沿水深方向的分布形式,在反弧段势流区任取一距壁面为y′的微元体为研究对象,假设沿微元体所在断面任一点的总能量保持不变,则有[19]:
(1)
式中:u为反弧段势流流速;H为反弧段任意断面以底板为基准的位置总水头;p为微元体动水压强;ρ为水的密度;g为重力加速度;θ为微元体所在断面与铅直方向的夹角,如图3所示。将式(1)对y′求导,忽略沿水深方向流层之间的能量损失,即∂H/∂y′=0,则有:
(2)
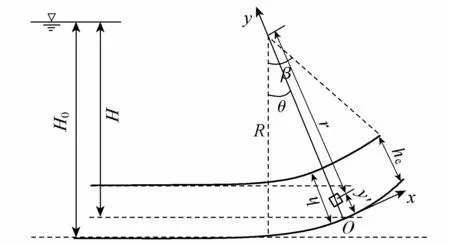
图3反弧段水流示意图
反弧段任一微元体的动水压强p由静水压强和离心力压强两部分组成,则p可用下式计算[20]:
(3)
式中:h为反弧断水深;r为微元体曲率半径,基于同心圆假设,有r=R-y′。将式(3)对y′求导后代入式(2),整理得到:
(4)
将式(4)移项、变形并积分,则有:
(5)
式中:Co为积分系数。
当y′ = 0时,流速u等于壁面势流流速uw,即u=uw,将其代入式(5)得出Co为
(6)
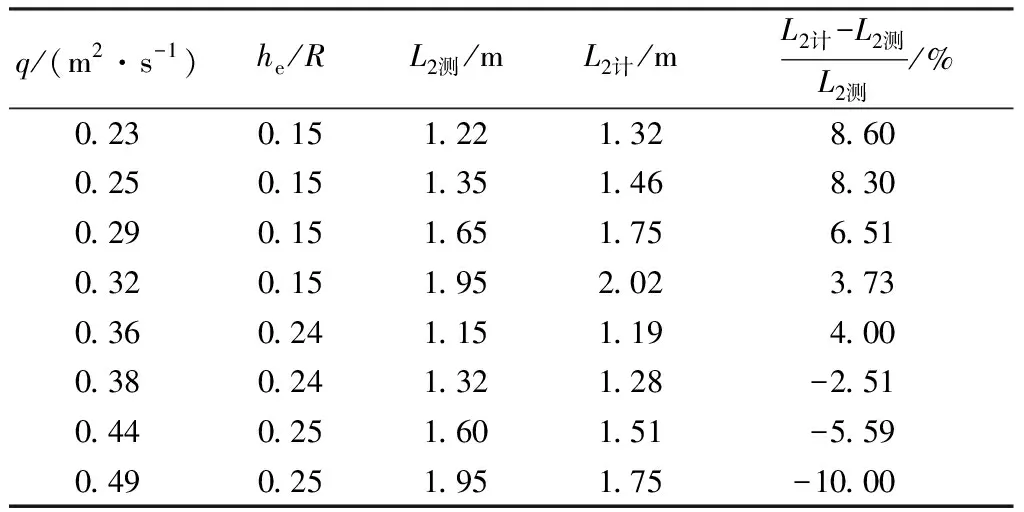
将式(6)代入式(5),在同心圆假设下有y′ (7) 式(7)即为本文得到的反弧段势流流速分布形式,其推导过程中,同时考虑了静水压强和离心力压强的影响。 如图3所示,设出坎断面水深为he,对反弧鼻坎,假设出坎水流沿he均匀分布,则沿he积分可得到单宽流量q: (8) 当y′ = 0时,u=uw;当y′ =he时,u=ua,其中ua为出坎断面的表面势流流速。为便于说明,设水舌上、下缘出射流速分别为v1和v2,并取v1=ua,v2=uw,则有y′ = 0时,v1=ua;y′ =he时,v2=uw。 在对式(8)积分时,需要用到出口断面水深he。工程中出坎断面水深通常不易测量,本文为方便计算,取出口断面水深he近似等于反弧底部水深,根据辛玉传[21]得到的反弧底部水深经验公式计算 (9) 式中:Ho为以反弧最低点为基准的上游水头;he/R为相对出坎水深。 将式(7)代入式(8),利用柯特斯积分公式积分得到: (10) (11) 式(10)和(11)分别为水舌上、下缘出射流速计算式。 以鼻坎出口底板位置为原点,利用抛物线公式计算挑距: (12) 由于没有搜集到关于水舌下缘挑距的其他模型或原型观测资料,因此,仅利用本文试验数据对反弧鼻坎水舌下缘挑距计算结果进行了验证,计算结果如表2所示,表中L2测为通过模型试验获得的下缘挑距,L2计为本文方法计算所得水舌下缘挑距。 由表1可知,本文方法计算的水舌上缘挑距与模型试验结果的最大相对误差为4.11%,与原型观测结果的最大相对误差为11.26%,而常规方法计算所得挑距与模型试验结果最大相对误差为12.27%,与原型观测结果最大相对误差则达到46.28%,表明尽管本文计算过程中没有考虑原型中水舌掺气和空气阻力对挑距的影响,但是本文方法对水舌上缘挑距的预测精度较常规方法高。 由表2可知,在本文试验范围0.15 ≤he/R≤ 0.25内,由出射流速计算式(11)得到的下缘挑距与模型试验结果的相对误差均在10.00%以内,表明本文提出的水舌下缘挑距计算方法具有较好的计算精度。 表1 水舌上缘挑距计算结果 表2 水舌下缘挑距计算结果 注:模型试验的R=0.5 m,β=45°,d=0.65 m。 a. 本文提出的基于出射流速的挑距计算方法计算的水舌上、下缘挑距与模型试验结果的最大相对误差分别为4.11%和10.00%,计算的水舌上缘挑距与文献[22]中原型观测结果的最大相对误差为11.26%,精度较高。 b. 本文计算方法适用于相对出坎水深为0.15~0.25范围,满足SL 319—2005《混凝土重力坝设计规范》中建议的R=(4~10)he,其超过该范围的适用性有待更多的实测资料验证。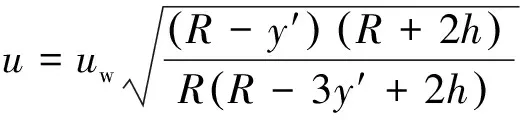
3 水舌上、下缘出射流速


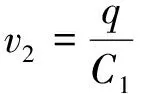
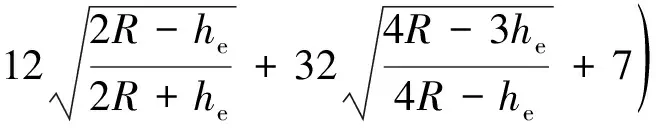
4 挑距计算
4.1 计算方法

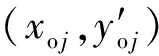
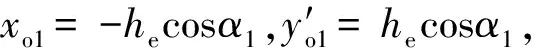

4.2 计算结果验证


5 结论
