长距离有压输水工程泵站水锤的数值分析

2020-05-19丁法龙茅泽育

水利水电科技进展 2020年2期

韩凯，丁法龙，茅泽育

(清华大学水利水电工程系，北京 100084)

为了解决地区水资源分布不均与部分城市水量供求紧张的问题，长距离供水工程的论证与建设得到了社会的普遍关注。水锤是一种有压输水工程中不可避免的水力过渡现象，在管线系统中引起剧烈的压力波动，产生结构振动和噪声，威胁工程的安全稳定运行，甚至导致水质下降和危及人民群众的生命财产安全[1-4]。学者们通过数值方法、模型试验、原型观测等方式对水锤现象开展了大量的研究[4-8]。由于长距离有压输水工程的部件及涉及的物理现象多而复杂，系统中不同的内边界条件相互之间又存在影响，而且水力过渡过程中的液柱分离现象具有较大的动态性，因此与水锤相关的研究一直受到人们的重视[9]。随着计算机技术的发展，越来越多的数值方法得以应用到水锤计算，常见的数值方法有特征线法(MOC)、有限差分法(FDM)、有限体积法(FVM)、有限元法(FEM)。为了提高数值计算的精度，结合各类数值方法，多种新型的数值格式被提出[9-13]。其中MOC方法由于具有计算方便有效、便于计算机编程、在考虑水头损失影响的复杂管道系统中适用性好等优点，在工程领域得到了更为广泛的应用[14-16]。

双吸离心泵站适用于流量大、管线长的输水工程，为了避免发生严重的泵站水锤，需要对其进行较为准确的水锤计算与分析。泵站水锤的水动力学特性对边界条件极敏感，不同工程的水锤特性可能存在较大差异，因此对长距离有压输水工程，尤其是在事故停泵时，针对个别重要影响因素进行敏感性分析和研究，了解水力过渡过程中水锤的动力学特性，对有压输水系统的安全稳定运行十分重要[17]。综合考虑多种内外边界条件，从有压输水工程的全系统角度出发，用数值方法开展的停泵水锤研究目前很少，尤其是对工程管线长度超过50 km的超长距离有压输水工程，国内外在相关领域的工程建设经验还很缺乏[18-19]。

本文以四平干线为例，综合考虑了长距离有压输水系统中的多种边界条件，以特征-差分方法为基础建立了长距离有压输水工程泵站水锤问题的数值模型,对事故停泵后重新启泵的时间间隔、输水系统管线糙率等要素进行了敏感性分析，并根据计算结果提出了相应建议，以期为相关的研究和今后的工程建设提供参考和借鉴。

1 数值模型

水锤现象可用一维非恒定有压管流的连续性方程和运动方程描述[5]：

(1)

式中：h为测压管水头；v为断面平均流速；x为管道轴线上的坐标，指向下游为正；θ为管轴线上水流方向与水平线的夹角，当高度沿x轴正方向增加时为正；a为水锤波波速；t为时间；D为管道直径；λ为Darcy-Weisbach沿程阻力系数；g为重力加速度。

用特征-差分方法求解水锤基本方程[7]，忽略特征线方程中的水流流速v，这样就将x-t平面划分成了如图1所示的矩形网格，两条斜率为±a的网格对角线即为特征线。在式(1)中，令dx/dt=±a，则特征方程可以写成以下形式[18]：

(2)

其中

CP=hi-1,n+Bqi-1,n-Rqi-1,n|qi-1,n|

CM=hi+1,n-Bqi+1,n+Rqi+1,n|qi+1,n|

式中：hi,n+1、qi,n+1分别为在t+Δt时刻节点i处的水头和流量；hi±1,n、qi±1,n分别为在t时刻节点i±1处的水头和流量；Δx、Δt分别为空间步长和时间步长；A为输水管道的截面积；f为管线的摩擦系数。

图1 特征-差分网格

2 输水工程概况与模型构建

2.1 输水工程概况

四平干线为吉林省中部城市引松供水工程中的一条干线，取水口位于总干线末端的冯家岭分水枢纽，终点为下三台水库，两者之间为大黑山主脉。输水线路总长97.32 km，有多个分水口、检修阀、空气阀、泄水阀、调压井、通风竖井等，沿线管道坡度变化由于地势原因也非常复杂。工程布置情况与管线高程H沿程变化情况如图2所示。可见，影响该输水工程供水设计和运行可靠性的因素众多，任意一处构筑物遭到破坏都将影响输水系统的正常运行。

图2 四平干线工程概况

泵站设计流量为8.8 m3/s，相应泵站出口压力线高程为256.78 m，管线末端处的中心线高程为211.58 m。根据设计资料，隧洞、预应力钢筒混凝土管(PCCP)、钢管(SP)设计糙率分别为0.014 0、0.011 5、0.012 0，由于工程资料存在不可避免的误差，且工程长期运行后必然会出现管壁损耗引起管道糙率增加，因此分别再选取4组糙率组合，针对这5组糙率组合进行了恒定流计算。糙率组合的取值以及由恒定流计算得到的下游边界条件如表1所示。

本文主要讨论泵站机组同时事故断电后，再次启机的时间间隔和管道糙率组合对输水系统沿程压力线、压力极值、调压井水位波动、泵站机组和泵后阀门受到的水动力荷载的影响。将模型设计为关闭所有分水口，泵站所有机组断电，泵后液压阀门按照设定程序进行启闭操作，经过不同时间间隔tg后所有机组和阀门再次启机运行。各设计工况的停泵时刻、再次启机的时间间隔、启泵时间等情况见表1。其中，通过工况K1～K5数值计算结果的对比可以分析事故停泵后再次启泵的时间间隔tg对停泵过程水力特性的影响；通过工况K6、K7、K8、K9、K1数值计算结果的对比可以分析不同糙率组合对停泵过程水力特性的影响。

表1 计算工况

注：hw为沿程水头损失；hd为管线下游段的压力水头值。

2.2 模型构建

数值模型共设有3个泵，3个泵后阀门，1个调压井，636个管段，93处空气阀。计算总时长取1 000 s，水力过渡发生前输水系统以有压恒定流状态运行。数值计算过程中关于无因次量、管长、管径、面积、压强、流量、流速、密度等主要变量的相对容许误差取0.001；时间步长取0.004 s；上游边界条件以泵站出口的压力高程线计；下游水位取水库的正常蓄水位213.60 m。水体的各项物性参数取值如下：密度为998.23 kg/m3，动力黏度为0.001 Pa·s，温度为10℃，体积模量为2.2 GPa，蒸汽压强为-0.1 MPa。

2.2.1泵

泵站机组采用卧式单级双吸离心泵(三用一备)，泵站机组的基本参数如下：额定水头hn=15 m，额定流量Qn=2.95 m3/s，额定转速Nn=425 r/min，额定功率Pn=560 kW，转动惯量J=185 kg·m2，额定效率ηn=89.2%。根据这些基本参数通过计算比转速得到泵站机组的无因次全特性曲线WH、WB[19]，结果如图3所示。

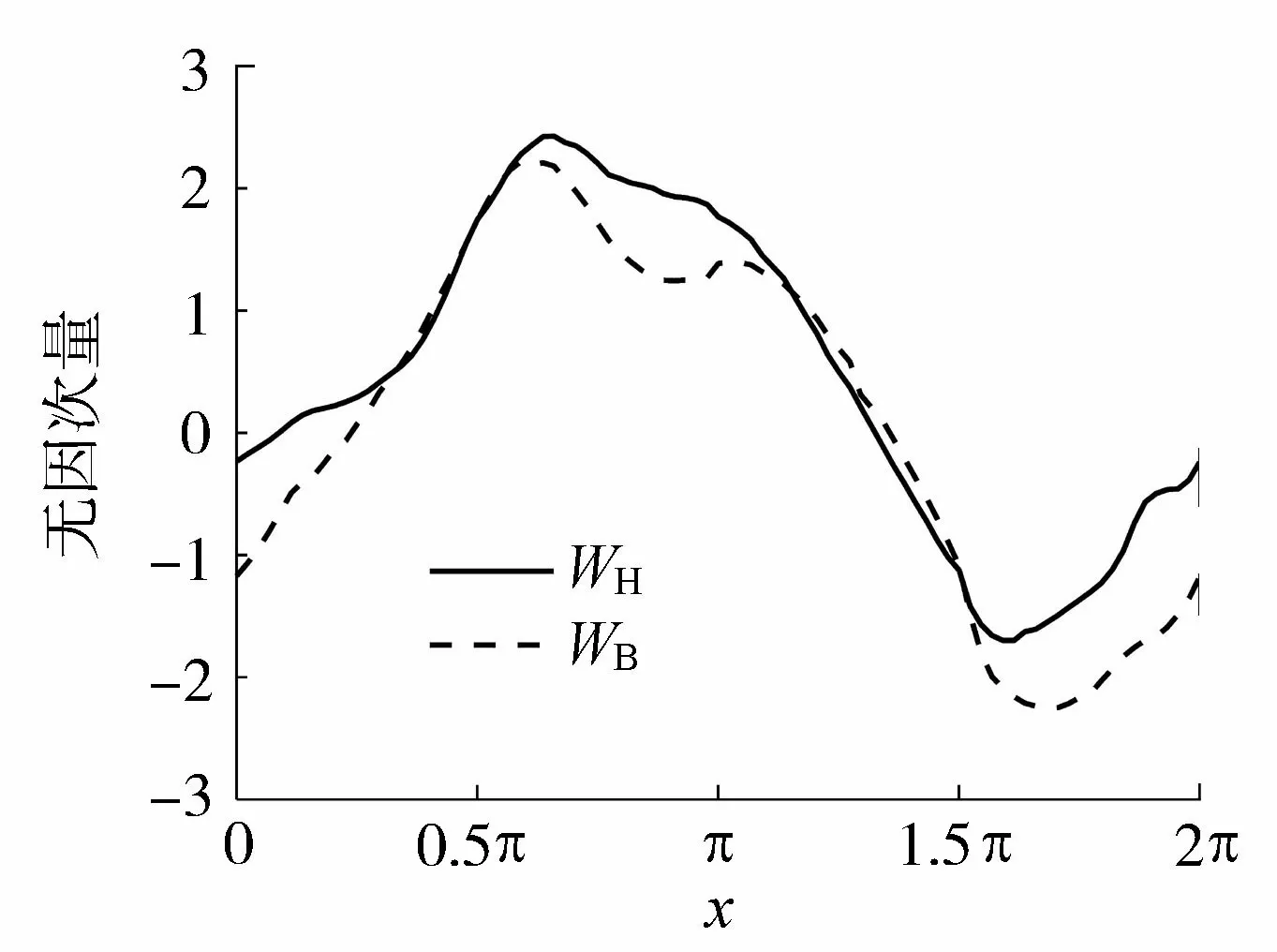
图3 泵的无因次全特性曲线

2.2.2调压井

四平调压井位于桩号1+286 m处，直径12 m，高度45.51 m，与之相连的管线为内径为4.0 m的压力隧洞，隧洞糙率取0.014，调压井的计算模型如图4所示。

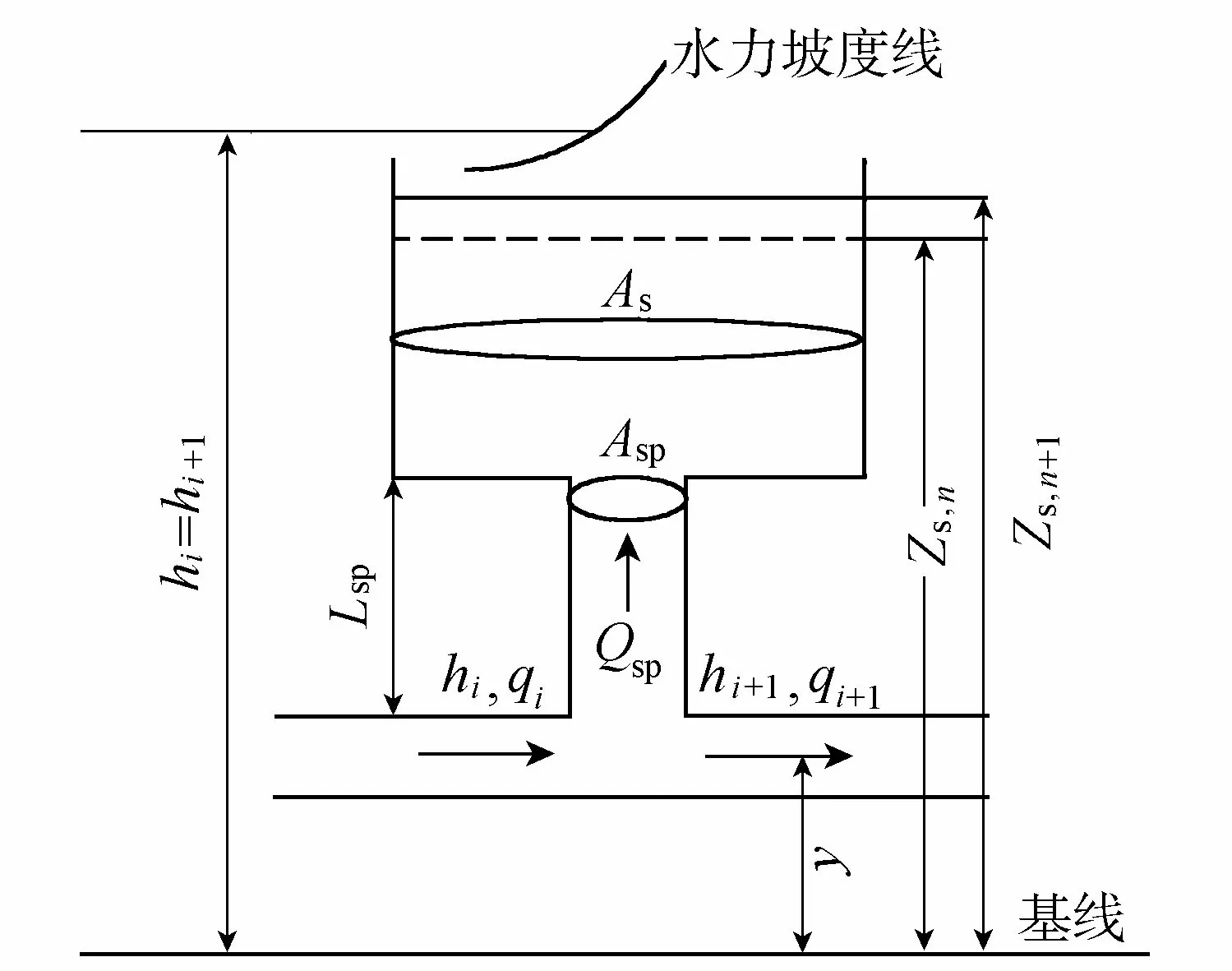
图4 调压井计算模型

调压井内水流连续性方程可用式(3)表示，立管的容积与整个输水系统相比，可视为一个集中质量点，若忽略节点i和节点i+1之间的水头损失，则管内流体的运动方程可用式(4)表示[2]。

qi,n+1=qi+1,n+1+Qsp,n+1

(3)

(4)

(5)

式中：As是调压井的横截面积。

2.2.3异性串联管

管径变化、糙率变化、约束条件变化或有其他特性变化的输水管道称为异性管道，长距离输水管线的异性管道多为单管串联，称为异性串联管[6]。图5描述了异性串联管在单管内部以及不同管段之间的边界条件，对于有压输水工程中产生的水锤，正向波波速v+a>0，逆向波波速v-a<0。在连接处两侧，设压力相等、流量连续，则

hi=hjqi=qj

(6)

联立式(2)和式(6)可直接解得

(7)

将q结果代入式(2)后，即可得出h。

图5 异性串联管的边界条件

四平干线输水管线共计636个管段，单管长度从2～3.6 km不等，管径从2.0～4.0 m变化。由于管线资料复杂，水锤波速又是一个较难精确确定的物理量，为使计算成本得到有效控制，需对PCCP、SP和圆形压力隧洞中的水锤波速进行简化计算[20]。结合工程实际资料，PCCP、SP、隧洞中水锤波速取值依次为950 m/s、1 000 m/s和1 230 m/s。将不满足库朗条件的短管设为压力瞬间通过管道，相应管段内流体的动量方程为

(8)

式中：Q、L1分别为短管流量、长度；ρ为流体的密度；p1、p2分别为管道入口和出口的压力。

当时间步长取0.004 s时，模型中636个管段中仅有5段短管，共10.89 m，仅占管线总长的万分之一，对计算结果的影响可以忽略不计。

2.2.4空气阀

空气阀的求解采用直接求解法[8]，分别将以亚声速流入和以临界速度流出空气阀的描述空气质量流量的方程式离散，并经一系列分段方程近似后，得到关于空气阀中气体压力的一元二次方程，然后通过判断解的存在区域并通过求解相应一元二次方程得到下一时刻的空气阀内的气体压力。

工程沿线共设置直径为0.3 m的空气阀90处，每台机组后各设1处空气阀，真空负压允许值为-3.0 m，气体排放系数取0.6。

2.2.5泵后阀门

为了有效控制输水水量和防止可能发生的水泵倒转，在泵后设置了液压缓闭蝶阀，进口管径1.4 m，出口管径1.2 m，对应于阀门有效截面积Af的流量系数CD与阀门开度τ(τ=Af/A0，其中A0为阀门全开时的过流面积)的关系如图6所示。通过阀门的流量qv可以表示为

(9)

式中：Δh为阀门两端的水头差。

结合式(2)，阀门端节点的水头可用下式计算：

(10)

式中：hvl,n+1、hvr,n+1分别为阀门端节点左、右两端在t+Δt时刻的压力水头。

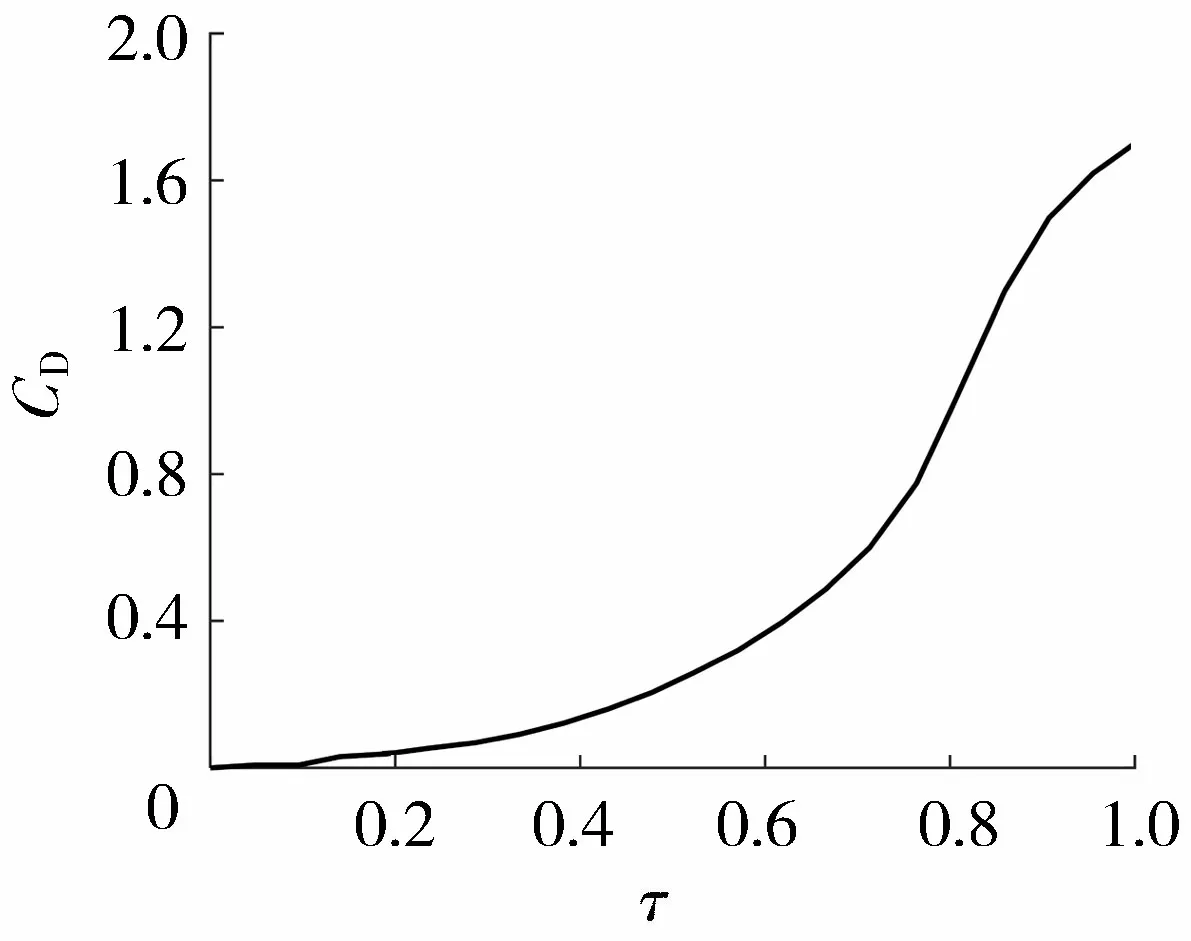
图6 泵后阀门的CD-τ关系曲线

GB 50265—2010《泵站设计规范》规定，扬程高、管道长的大中型泵站，事故停泵可能导致机组长时间超速反转或造成水锤压力过大，推荐在水泵出口安装两阶段关闭的液压缓闭阀门。根据水锤基本理论和系统实际情况，在数值模拟分析的基础上优化，本文最终选用的阀门启闭规则如下：①两阶段折线关闭，第一阶段为快关，即在5 s内关闭30%的开度，剩余70%的开度则在55 s内慢关；②60 s内匀速开启。

3 结果与讨论

3.1 模型计算结果

图7为数值计算得到的工况K1的压力线高程。由图7可知，最低压力线高程位于管线高程之上，设计的联合水锤防护措施可以有效应对停泵引起的负压；压力水头最大值出现在里程x=57.684 km处，即管线高程最低点，这是因为在该处除了存在位能和压能的转化之外，管线坡度剧烈变化引起的液柱分离与断流弥合水锤进一步增大了该区域的压力极值；事故停泵之后，泵后产生较大的水锤降压波并沿输水管线向下游传播，在空气阀和管线摩阻的作用下，水锤波沿程不断衰减；沿程最低压力出现在泵后1 km管线范围内。

图7 工况K1下沿程压力线高程

图8 各工况条件下水锤压力对比

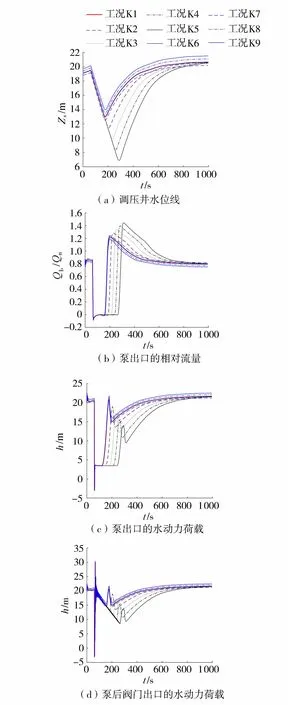
图9 不同工况数值计算结果对比

图9为K1～K9工况下调压井水位、泵出口相对流量(实时流量与额定流量之比，Qb/Qn)、泵出口水动力荷载、泵后阀门出口水动力荷载的变化情况。停泵(t=60 s)首先引起水锤降压波，造成桩号1+286 m处的调压井水位在停泵后随即降低，启泵后经过一段时间又逐渐恢复到稳定水位。相应地，泵出口的流量变化主要取决于泵的运行状态，阀门完全关闭(t=120 s)之前虽然出现短暂的倒流现象，但由于关阀程序设置合理，倒流量较小，符合GB 50265—2010《泵站设计规范》要求。泵出口的水压由于停泵骤减至4 m的瞬时负压，并快速回升至3.5 m的压力水头，启泵引起该处的水压迅速升高而后又降低了5 m的水头，即产生了启泵水锤。相比于泵出口，泵后阀门承受的水动力荷载更为不利，瞬时最大正压力水头达到30 m，最大压力水头差接近35 m，存在剧烈波动；在摩阻作用下，这种波动又快速衰减，形成阻尼振荡。

3.2 分析讨论

模型计算结果表明四平干线输水系统沿线构筑物布置和阀门启闭规则设计合理，能够保证四平泵站机组以及沿程管线和构筑物在发生事故停泵后能够安全、迅速地完成水力过渡过程，保证了输供水系统事故时能够及时响应。但启泵的时间间隔tg和管线糙率这两个要素对最终的计算结果仍有着不同程度的影响。

四平长距离有压输水工程的水锤波传播周期T(T=2L/a，其中L为管线总长度)接近200 s，工况设计的启泵间隔时间tg设计在120～240 s之间。由图9可知，启泵时间间隔tg对输水系统的水锤防护存在重要影响：①停泵引起减压顺波，在经下游水库反射传回增压逆波之前，上游端调压井的水位将逐渐下降，而启泵过程可以产生增压顺波，使调压井水位提前回升，因此设计较小的tg有助于减小长距离有压输水工程的调压井尺寸及相应工程造价；②tg越小，启泵水锤引起的泵出口瞬时流量越大，对应的瞬时荷载越大；③tg越小，泵后阀门承受的压力波动越剧烈，对机组的安全稳定运行也就越不利。

根据以上计算结果与分析讨论，对长距离有压输水工程的规划与设计提出以下建议：①工程涉及的部件众多，多种边界条件之间存在相互影响，个别设计条件的变化可能会对全系统产生重大的影响，因此每项设计都应根据实际工程资料，综合考虑各种边界条件，对水力瞬变特性开展研究，为水锤防护提供参考；②在泵站水锤中，事故停泵后的启泵时间间隔对水力过渡过程具有重要影响，须保证泵站机组连同泵后阀门在事故断电或甩负荷后按照设计程序运行，避免机组直接承受水力过渡引起的压力振荡，防止机组出现倒转工况，减少水量和水能损失；③虽然管线糙率对全系统的水动力特性影响较小，但摩阻引起的水能损失十分可观，在工程建设过程中仍应把好工程质量关，控制管线糙率在设计范围内，此外，除了对工程沿线构筑物进行定期的检查和维护，还需对可能出现的管道磨蚀、低等水生生物附生等不利情况进行监测与防治。