Fractal features and infiltration characteristics of the soil from different land uses in a small watershed in a rocky,mountainous area in Shandong Province

Lei Wang · Rui Yang · Shuyong Zhang · Guangcan Zhang · Xia Liu

Abstract We studied infiltration and fractal mechanisms on sloping farmlands in a small watershed in Shandong Province in the rocky mountain areas of northern China. We studied soil fraction and soil water retention curves, and developed a soil infiltration model to analyze its quantitative relationship with soil particle size and pore dimensions under four types of land use, including sloping farmland, abandoned land, natural forest, and forest plantation (Malus pumila,Crataegus pinnatifida).Soil stability infiltration rate ranked as sloping farmland ＞abandoned land ＞natural forest ＞forest plantation.The sequence of soil particle size and pore dimension ranked as natural forest ＞forest plantation ＞abandoned land ＞sloping farmland. There were significant positive correlations between soil particle size and pore dimension,and both were positively correlated with the percent volume of silt and clay. They were negatively correlated with soil infiltration rate.The Horton model and the power function model were more suitable for simulating soil infiltration and the infiltration rate. We concluded that the soil in this area displayed typical fragments of rocky mountainous regions due to the loss of silt and clay caused by cultivation on sloping farmland.The uniformity and fractal dimensions of soil particle sizes and pore distribution decreased, thereby enhancing soil infiltration capacity and decreasing soil water retention capacity.

Keywords Soil structure · Soil infiltration · Fractal dimension · Sloping farmland · Rocky mountainous area

Introduction

The distribution of soil particles and pores is an important physical property of soil and is closely related to the hydrological process and the characteristics of water mechanics in soil (Bartolo et al. 2014; Globus 2006).Therefore, soil infiltration is one of the most important hydrological processes that affects soil properties (Cheruy et al. 2013). Owing to its strong influence on rainfall (or irrigation) redistribution (Nearing et al. 2017; Panagos et al. 2017), surface runoff (Peng et al.2006;Brooks et al.2013),soil erosion(Jomaa et al.2013;Martínez-Hernández and Rodrigo-Comino 2017)and nutrient migration(García-Díaz et al. 2017), soil infiltration has been an important focus of soil and water conservation studies (Thierfelder and Wall 2009; Boluwade and Madramootoo 2016; Alaba and Chandra 2016; Sayah et al. 2016). Infiltration is not only closely related to natural factors, such as soil texture,composition and structure, but also is influenced by land use and tillage methods(Chen et al.2005;Veit et al.2014).The infiltration rate, especially the rate of steady infiltration,reflects the infiltration capacity of soil.The infiltration rate is an important index used to characterize infiltration performance and, to a certain extent, to characterize soil permeability ventilation performance and water-holding capacity and how the infiltration capacity coordinates these features.When the infiltration rate is too high or too low,it is not conducive to soil water and nutrient conservation or plant growth (Zhang 2006). Studies of soil infiltration performance have been reported for different regions (or small watersheds) (Thierfelder and Wall 2009; Boluwade and Madramootoo 2016; Alaba and Chandra 2016; Sayah et al. 2016). In studies of sloping farmland and abandoned land,the soil infiltration rate relationships between sloping land and other land use/cover types have proven to be inconsistent (Bagarello et al. 2014; Comino et al. 2016).Some results have indicated that the soil stabilization rate of sloping land was less than that of grasslands (Dong 2004; Chen et al. 2005), forest land (Veit et al. 2014) or terraces (Yan et al. 2013), and others were obviously higher (Peng et al. 2006; Dong 2004).

In recent years,fractal theory has been used to quantitatively study soil structure and its hydraulic characteristics(Bartolo et al. 2014). Soil structure (particle size, surface area, volume, pore size, etc.) has self-similar and obvious fractal characteristics and can be described by the Sierpinski Carpet and Menger Sponge Model (Tao and Zhang 2009;Bartoli et al.2010;Tao et al.2012).The concept of the fractal dimension of soil particle volume was proposed to evaluate the soil fractal characteristics of farmland and a tea plantation(Zolfaghari et al.2016).A method for characterizing soil fractal characteristics by particle size distribution was proposed in a study of the relationship between soil particle size distribution and the corresponding mass distribution (Filgueira et al. 2006). Tyler and Wheatcraft (1990) used the Sierpinski carpet structure model, Huang and Zhan (2002)applied the Menger sponge model, and Rieu and Sposito(1991a, b) used pore size self-similarity to develop a soil water characteristic curve model to reflect the relationship between soil pore structure and soil water retention characteristics(Bartolo et al.2014;Feng and Pang 2009).At present,these methods have been applied to quantitatively study soil particle structure(Globus 2006;Dong and Zheng 2009)or pore structure under different land use/cover types, but with respect to soil infiltration.There are few studies on the quantitative relationship between soil infiltration performance and the fractal characteristics of soil structure(Jiang et al.2005;Wang and Wang 2007).

The aim of this paper was to study sloping farmland,abandoned farmland, natural forestland and forest plantation land in a small watershed in the middle of a mountainous area in the Shandong Province using soil hydrology and fractal principles.The effects of land use management are discussed in regards to soil infiltration,soil particle size and pore structure.

Materials and methods

Study area

Our study area was located in the Mengpo small watershed of Tumen Town,Yiyuan County,in the hinterland of Luzhong Mountains,in the middle of Shandong Province in the rocky mountain areas of northern China. It lies at E117°54′-118°31′,N35°55′-36°23′(Fig. 1).Mean annual temperature and precipitation are 11.9 °C and 720.8 mm, respectively,and this area has a warm temperate semi-humid monsoon climate.There is a frost-free period of approximately 189 d.Average annual sunshine is 2660.6 h.The topography of the watershed is characterized by low mountains and hills,with elevations ranging from 300 to 500 m above sea level.The parent rock material is granite-gneiss and limestone.The soil depth is ＜40 cm,and the soil is coarse-grained sandy with high grit content.The main land use types in the study area include farmland, forest plantation and natural forest, with sloping farmland accounting for more than 80%(Yao et al.2008).Soil erosion is a serious issue(Chen et al.2009).In this small watershed, the plant species include more tree species, e.g., Pinus densiflora, Robinia pseudoacacia,Quercus acutissima, Malus pumila, Castanea mollissima

and Crataegus pinnatifida;the natural species include more shrub species, e.g., Lespedeza bicolor, Vitexnegundo heterophylla,Poa annua,Roegneria kamoji,Artemisia argyi and Rubus parvifolius.

Experimental sites and test layout

Four types of land use (sloping farmland, abandoned land,forest plantation and natural forest)were investigated in the study area (Table 1). Sloping farmland has been tilled for approximately 20 years; the return period of abandoned land has been 5-6 years; the natural forest has been dominant in R. pseudoacacia and P. densiflora for approximately 20 and 30 years, respectively, and the forest plantation underwent terrace construction and stand cultivation for a period of 20 years and is dominated by M.pumila and C. pinnatifida.

Three experimental sites were established on each land use type with three plots selected in a diagonal line along each experimental site.Each test sample was repeated three times for observation or sampling(averaging analysis),and the measured soil thickness was in 0-30 cm,with a total of 36 soil samples.

Fig. 1 Location of the study area

Table 1 Survey of different land uses in the study area

Measure particle size distribution (PSD)and fractal dimension

All the soil samples were air-dried and passed through 2 mm sieves prior to laboratory analysis in order to remove roots and other debris.To measure soil particles and fractal characteristics, the soil samples were pretreated in an H2O2solution(30%,w/w)to destroy the organic matter.HCl was added to remove the carbonate. The soil aggregates were then dispersed by adding sodium hexametaphosphate(NaHMP) and sonicating the samples for 30 s (Andreola et al.2006).The pretreated soil samples were analyzed using a laser diffraction technique of Malvern MS2000(Malvern,England), with measurement ranges and errors of 0.02-2000 μm and ＜2%, respectively. Each sample was measured three times for the arithmetic mean value.The results of the soil PSD were related to the soil texture classification system (Twarakavi et al. 2010) (American system). The measured particle size was divided as follows: clay (0-2 μm), silt (2-50 μm), fine sand (50-100, 100-250 μm),coarse sand (250-500, 500-1000 μm), and gravel (1000-2000 μm).The fractal dimensions of soil PSD were calculated based on the volume distribution of soil particle size as:

where r is the soil particle size,R is the soil particle size of the grade,Rmaxis the mean diameter of the largest particle grade,V(r ＜R)is the volume of soil particle sizes less than R, VTis the volume of all the soil particles, and D is the volume-based fractal dimension.

Measured soil water retention curve (SWRC)and pore fractal dimension

All the soil samples were obtained with a ring knife from the experimental sites. SWRC was determined using a H-1400PF centrifuge, which was fitted for the pore fractal dimension, and the Menger corpus structure derived the SWRC model based on Huang and Zhan (2002):

where D′is the fractal dimension of the pore volume,θ,θsis the unsaturated and saturated moisture content, respectively, and Ψ, Ψaare the matrix potential and inlet matrix potential,respectively,when the water content is θ.SWRC was fitted to the power form using a formula where Ψ is ordinate and θ is abscissa,the resulting power in the fitting curve isand the fractal dimension of the pore was calculated (D′).

Measurement and model simulation of the soil infiltration process

The soil infiltration process curve was determined by the single loop quantitative water adding method. The Philip model, Horton model and power function model were also used to analyze the soil infiltration process (Mirzaee et al.2014; Mousavi 2015; Jejurkar and Rajurkar 2015). The abovementioned expression (infiltration rate, f and time,t relation) is as follows:

Philip model

where a is the empirical parameter, and b is equivalent to the rate of steady infiltration.

The Horton model can be defined as follows:

where f0is the initial infiltration rate (0-5 min) (Chandrakant and Milind 2015; Herrada et al. 2014), fcis equivalent to the steady infiltration rate,and k is a constant.

Finally, the Power function model can be defined as follows:

where a,b and n are empirical constants;b is equivalent to the steady infiltration rate; and n is the attenuation index.

Data processing

Correlation analysis of different land use types was performed by the Least-Significant Difference (LSD) method for multiple comparisons. The difference was extremely significant when p ＜0.01, the difference was significant when p ＜0.05,and the difference was not significant when p ＞0.05.

Results

Soil particle composition and fractal features of different land uses

Soil particle size distribution (PSD)

The PSDs varied by land use type (Table 2). The predominant soil particle size (volume fraction, similarly hereinafter) was fine sand, ranging from 31.8 to 51.8%.This was followed by coarse sand, ranging from 23.8 to 37.0%. The contents of gravel sand, silt and clay were all relatively low. Gravel sand accounted for 10.5-20.9%,while silt sand ranged from 10.7 to 13.1%.Finally,the clay sand ranged from 0.5 to 1.1%. The content of sand in soil was obviously higher than that of silt and clay, and this shows that the soil types in this area are typically comprised of coarse sand and gravel (Zhan et al. 2009).

Soil particle fractal dimension, pore fractal dimension and their relevance

The soil particle fractal dimensions of four types of land use rangedfrom2.20to2.33(Table 2).Indeclining order,particle fractal dimensions ranked as ecological forest ＞economicforest＞abandoned land ＞sloping farmland. Soil particle fractal dimension varied significantly between sloping farmland,natural forest and forest plantation.Other comparisons showed no difference.The soil pore fractal dimension ranged from 2.74 to 2.85(Table 2)and exhibited the same result as the D value, i.e. natural forest＞forest plantation ＞abandoned land＞sloping farmland.Pore volume varied between sloping farmland, natural forest and forest plantation. The differences between other land uses were not significant.Soil particle fractal dimension had a significantly linear positive correlation with pore fractal dimension(Fig. 2).The expression was D=0.6711D′＋1.2692,and the correlation coefficient R was 0.957.

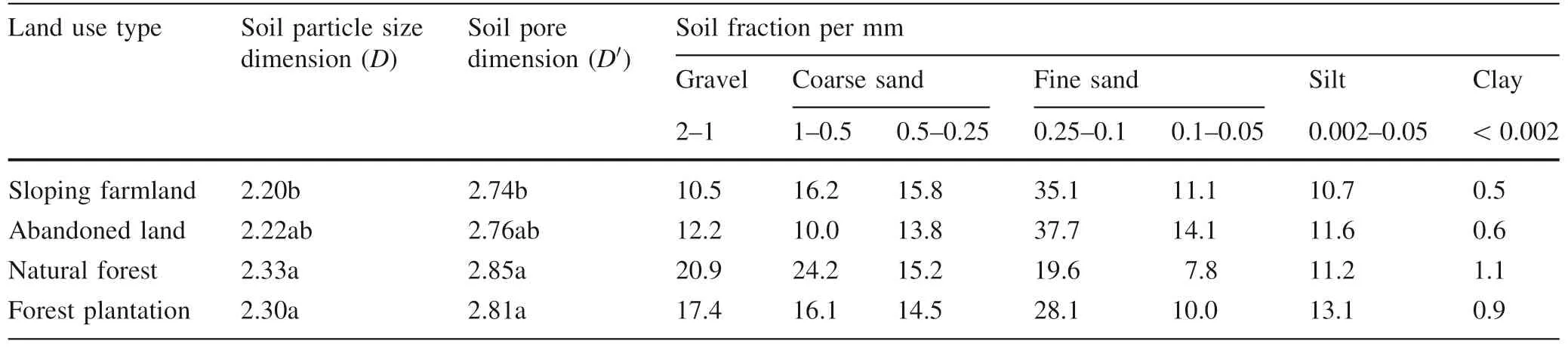
Table 2 Soil particle composition, fractal dimension and pore fractal dimension of different land uses in volume (%)

Soil particle composition, particle fractal dimension,and pore fractal dimension and their relevance

Particle fractal dimension (D) and pore fractal dimension(D′)were consistent with soil particle composition(Fig. 3).D and D′were positively correlated with Soilclay,sand and silt contents (Fig. 2c, d), and they had a significantly negative correlation with the soil sand content (Fig. 2b),but not with the content of soil gravel (Fig. 2a). This indicates that D and D′clearly characterized the clay, silt and fine sand contents of the soil. Therefore, larger values of D or D′correlated to a greater content of clay and silt in the soil, and lower sand content. The values of D and D′did not clearly reflect the level of gravel content in the soil.

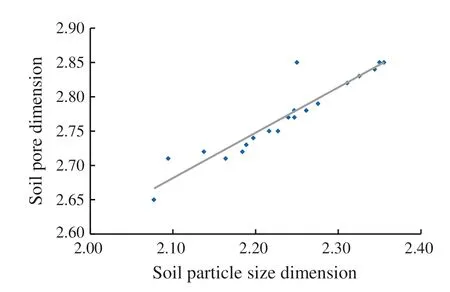
Fig. 2 Relationships between soil particle fractal dimension and pore fractal dimension

Characteristics of soil infiltration under different land uses

Infiltration rate of soil and its relationship to the particle fractal dimension and pore fractal dimension

Soil initial infiltration rates varied by land use type and ranked as follows(Table 3):sloping farmland ＞economic forest ＞abandoned land ＞ecological forest. Steady soil infiltration rate (fcmeasured value) ranked as sloping farmland ＞abandoned land ＞natural forest ＞forest plantation. Steady soil infiltration rate and initial infiltration rate had a linear negative correlation with either the soil fractal dimensions (D) or pore fractal dimensions (D′)(Fig. 4). The correlations between D and D′and the soil steady infiltration rate were significant, as was the initial infiltration rate. The soil infiltration rate decreased significantly with an increase in either D or D′.

Models of the soil infiltration process and its characteristic parameters

Regarding the fitting effects of the different models(Table 3),the Horton model, power function model and Philip model have good fitting degree to soil infiltration process,the coefficient of determination(R2)was ＞0.95 and differed significantly in the fitting results of the steady soil infiltration rate.The fitted value of the Horton model was higher than that of the measured steady permeation rate,with a fitting error percentage ranging from 1.7 to 12.8%among the different land uses.The fitting value of the power function model was low;the error percentage ranged from 6.7 to 20.3%.The steadysoil infiltration rate fitted by the Phillips model was smaller than the measured value, with an error percentage ranging from 83.7 to 129.8%among the land uses.The Horton model and the power function model were more suitable for simulating the soil infiltration process and steady infiltration rate in the study area;the Horton model was better for the degree of fit.

Fig. 3 Relationships between soil particle composition, particle fractal dimension and pore fractal dimension

Table 3 Measurement and fitting parameter of soil infiltration characteristics by land use type

Discussion

Fig. 4 Relationship between the soil fractal dimension and soil infiltration rate

The relationships between the soil infiltration rate of sloping farmland and other land uses in this study (Table 3) are consistent with those from a study in the southern red soil region and northern Shanxi loess region, where the rate of soil infiltration on sloping farmland is higher than that on arbor shrub land and grassland (Peng et al. 2006; Dong 2004).But the infiltration rate differs from that of other loess regions(Chen et al.2005;Dong 2004;Veit et al.2014)in that the soil stabilization rate of sloping farmland was less than that of forestland and other land use types.This is related to soil texture and the structural characteristics of the study area.Soils on our site were coarse-grained sandy-sand,high in grit content,but the contents of powder and clay were low(Table 2). In particular, the clay content of soil under different land uses ranged from 0.5 to 1%.This type of soil is usually characterized by coarse texture,low uniform particle distribution and pore distribution, and even low fractal dimension,with strong soil permeability and a weak capacity to sustain water and nutrients (Lin 2002). One of the important reasons for this is the lack of fine particles and water-holding pores in the soil (Yu et al. 2011). Soil loss caused by the cultivation of sloping farmland reduces the content of fine grains in the soil and the filling capacity of the soil space(Huang and Zhan 2002;Dong and Zheng 2009).This reduces the soil aggregate structure, and the waterholding pores reduce the uniformity of the soil particles and pore distribution, indicating that soil with lower fractal dimension and pore fractal dimension will have a larger infiltration rate(Tables 2,3).

The Horton model and the power function model were more suitable for simulating the soil infiltration process and infiltration rate.The Philip infiltration model was a poor fit,as the results indicate a large deviation from the measured values (Table 3). This might have been related tofactors affecting the infiltration process of soil and because the different models have their own characteristic parameters,boundary conditions, applicable conditions and limitations(Cerda 2010). For example, the reasons for the poor applicability of the Phillips model may be related to the fact that the exponential t in the formula is constant and difficult to adapt to soil infiltration changes at different prewater levels, or it is difficult to meet the model’s requirement for a lower initial water content (Zhan et al. 2009).

Conclusion

The steady soil infiltration rate on sloping farmland was significantly greater than that on abandoned land, forest plantation and natural forest in a small watershed. In contrast,the soil particles and pore fractal dimensions were significantly lower than those under other land uses(Table 2). There was a significant negative correlation between the soil infiltration rate, soil fractal dimensions and pore fractal dimensions in the small watershed. The soil particle size fractal dimensions and pore dimensions were significantly positively correlated with the silt, clay and sand contents. That is, changes in the content of silt and clay in the soil,the distribution of soil particles and the pore size had a significant effect on the infiltration performance of the soil.