Do increasing respiratory costs explain the decline with age of forest growth rate?

P. W. West

Abstract Once forests have achieved a full canopy, their growth rate declines progressively with age. This work used a global data set with estimates from a wide range of forest types, aged 20-795 years, of their annual photosynthetic production (gross primary production, GPP) and subsequent above- plus below-ground biomass production (net primary production, NPP). Both GPP and NPP increased with increasing mean annual temperature and precipitation. GPP was then unrelated toforest age whilst NPP declined progressively with increasing age. These results implied that autotrophic respiration increases with age. It has been proposed that GPP should decline in response to increasing water stress in leaves as water is raised to greater heights as trees grow taller with age. However, trees may make substantial plastic adjustment in morphology and anatomy of newly developing leaves, xylem and fine roots to compensate for this stress and maintain GPP with age. This work reviews the possibilities that NPP declines with age as respiratory costs increase progressively in, any or all of, the construction and maintenance of more complextissue, the maintenance of increasing amounts of live tissue within the sapwood of stems and coarse roots, the conversion of sapwood to heartwood, the increasing distance of phloem transport, increased turnover rates of fine roots, cost of supporting very tall trees that are unable to compensate fully for increased water stress in their canopies or maintaining alive competitively unsuccessful small trees.

Keywords Primary p roduction · Photosynthesis · Respiration · Biomass g rowth · Ageing

Introduction

Interest in the growth behaviour of forests includes the amount of wood they produce to be harvested for human use, the net amount of CO2sequestered within them in the context of mitigation of climate change or simply their part in the biodiversity of life on earth. The growth of a forest ecosystem (or plant ecosystems generally) is a consequence of the photosynthesis (excluding losses due to photorespiration) undertaken by the leaf canopy (sometimes combined with stem photosynthesis). This is known as “gross primary production” (GPP). Some of the photosynthetic production is then lost through “autotrophic respiration” as the plants undertake the wide range of metabolic processes essential to their life and which use energy derived from the glucose produced in photosynthesis. After these losses, the “net primary production” (NPP) of the ecosystem is made up of the growth that occurs in individual plant sizes (that is, their biomasses above- and below-ground combined) summed over all the plants of the ecosystem that remain alive during the growth period (plus that of ingrowths). Rather confusingly, NPP is often referred to as “gross growth rate” in forest measurement practice (Avery and Burkhart 2002).

In mathematical terms:

where RAis autotrophic respiration. Various units are used for these three variables: in the present work they will be expressed as an amount of carbon (stored in biomass or taken in or released as CO 2 ) per unit ground area on which the forest is growing per unit time (that is, g C m -2 year -1 ). Note that it is quite possible to refer to GPP, NPP and autotrophic respiration of individual plants (units then as g C year -1 plant -1 ), but throughout this work the terms will refer to stand based production. Autotrophic respiration is commonly considered to be the sum of “construction” and “maintenance” respiration ( RCand RM, respectively), that is:

Construction respiration is a consequence of energy used in the metabolic processes involved in constructing new and replacement tissues as well as the taking up from the soil, by fine roots, the mineral nutrients those tissues require. Maintenance respiration derives from the metabolic costs of operating living tissue; this includes repairing cell membranes, synthesising protein and maintaining ion gradients across cell membranes.

During the early lifetime of a forest stand, its NPP increases with age as seedlings grow. The canopy and fine root systems of the forest expand until they have developed fully. Thereafter, NPP starts to decline. This decline may start after only a decade or so, then continues progressively throughout the lifetime of the forest and may continue for hundreds of years. The decline usually occurs also in above-ground biomass and stem wood volume production (Gower et al. 1996); this is of obvious concern to commercial forestry.

There have been numerous suggestions over the last 50 years or so to explain why this decline of NPP with age occurs. Many of those suggestions have been discounted in reviews of the issue (Ryan et al. 1997, 2006) and other work (e.g. Barnard and Ryan 2003; Ryan et al. 2004) and need not be considered further here. The principal hypothesis that remains is known as the “hydraulic limitation theory”, proposed initially by Ryan and Yoder ( 1997). It suggests that trees must maintain a minimum water potential in their leaves in the face of increased resistance to water movement from roots to leaves as trees grow taller with age. Without this, it is believed stomatal closure will be more frequent, from time to time seasonally and during the day, reducing overall canopy conductance and photosynthetic production, that is, GPP.

The present work brings together three previously existing data sets that included estimates of GPP and/or NPP from a broad range of forest types of differing ages scattered widely around the globe. Relationships are established for both GPP and NPP with forest age and some other climatic factors. The results suggest that GPP does not decline with age. However, due to progressively increasing autotrophic respiration, NPP does. The Discussion then includes a review of the literature to explain what prevents the GPP decline that the hydraulic limitation theory proposes and what respiratory losses may, instead, contribute to the decline of NPP.

Data

The data set used here brought together estimates of forest GPP and/or NPP made by many different research groups over many years. Data for 97 sites were compiled by Luyssaert et al. ( 2007) (note the critical assessment of this data set in the Supplementary Information of Kutsch and Kolari 2015), Campioli et al. ( 2015) provided data for 24 sites and DeLucia et al. ( 2007) gave data for a number of unnamed sites. These data came from forests of every continent (excluding Antarctica of course), from hardwoods and softwoods and from cold, temperate and tropical regions; Fig. 1 shows how widespread geographically were the sites included in the largest data set used here (that of Luyssaert et al. 2007). At the time of their measurement, the forests in these data sets varied in age over the range 1-795 years. For the present work, only data from forest aged 20 years or more was considered; this allowed for the fact that GPP and NPP increase with age during the early life of the forest, as discussed in the Introduction. This choice of 20 years of age was made somewhat arbitrarily after inspection of the whole data set suggested that rather low values of GPP and/or NPP did occur in some forests below this age.

Fig. 1 Reproduction of Fig. 2 of Luyssaert et al. ( 2007) showing the geographical distribution of sites included in their data set. Reproduced by kind permission of John Wiley and Sons © 2007 The Authors, Journal Compilation © 2007 Blackwell Publishing Ltd.

There were four basic techniques used to measure GPP and NPP in these data sets. They are described in some detail in Supplementary Appendix A. In brief they were:“ Biomass pool” methods-these involve destructive measurement on and under the ground by weighing forest biomass and its changes over time. These methods may give reliable estimates of NPP, often with results for various tree parts separately (leaves, branches, stem, and roots etc.), “ Chamber” methods-these involve the use of instruments small enough to enclose tree parts (a few leaves, a clump of fine roots, a small area of stem) or a small area of the soil surface and measure gas (particularly CO2and/or water vapour) exchange between the plant part or soil surface and the atmospheric air contained within the chamber. They can be used to estimate photosynthetic and respiration amounts, but only over small parts of the tree or soil surface at a time and only for limited time periods. It can be difficult to scale these results up to give estimates for extended time periods over entire trees, entire forest stands or large soil areas, “ Eddy covariance” ( known also as “ eddy fl ux” or “ eddy correlation”) methods-these employ micro-meteorological instruments positioned above the canopy of the forest. These instruments measure gas exchange between the forest below and the atmosphere. These methods can be used to give continuous measurements over extended time periods for a full forest canopy. It is believed that these methods have tended to underestimate net carbon exchange to some extent (e.g. Speckman et al. 2015; Campioli et al. 2016). Such bias will undoubtedly exist in estimates of GPP and NPP that relied on these methods in the present data set. There have been various methodological developments aimed at removing these uncertainties (Tan et al. 2017; Hayek et al. 2018), “ Model- based” methods-these use previously developed model systems that were devised for the purpose and that are based on known physiological properties of the forest concerned. Such models are difficult to build and their effi cacy is often uncertain when applied to sites and forest circumstances outside those for which they were constructed.

These techniques can be complex and difficult to apply, especially for stands of appreciable area in forests with large, tall trees. Inevitably there is considerable uncertainty in estimates made using them. Luyssaert et al. ( 2007) attempted to quantify these uncertainties (using methods employed subsequently by Campioli et al. 2016). Their conclusions suggested that chamber and model-based methods generally give less certain estimates than eddy covariance or biomass pool techniques. Speckman et al. ( 2015) and Campioli et al. ( 2016) have compared results from eddy covariance and biomass pool methods whilst Zheng et al. ( 2018) have reviewed the use of model-based methods.

In the present data set, the sources from which Luyssaert et al. ( 2007) obtained their NPP estimates had used biomass pool methods. For GPP, about 76% of their sources had obtained estimates using eddy covariance techniques whilst about 12% had measured NPP by a biomass pool method and then added to it an estimate of autotrophic respiration. The remaining 12% had used model-based methods to estimate GPP. A similar mix of techniques had been used by the sources from which Campioli et al. ( 2015) and DeLucia et al. ( 2007) obtained their data. Whilst it must be recognised that there is both uncertainty and some potential for bias in many of these estimates, they do at least form a coherent and apparently carefully compiled data set that should provide some useful information about both GPP and NPP in a wide range of forests of different ages.

About two-thirds of the sites included in the present data set had only a single measurement made of GPP and/or NPP, a little under one-fi fth had 2-5 measurements and the rest had more than five measurements, the most being 32 measurements at one site. Most measurements were made over a 1 year period; this is an appropriate measurement period for these variables, since forest growth rates may change appreciably over periods longer than that. NPP was not measured at each measurement of each site. In total there were 433 measurements of GPP, but only 90 of NPP. The data set of Luyssaert et al. ( 2007) included measurements at some sites of the mean annual temperature and annual precipitation over the growth period concerned. Table 1 summarises the data that were available here.

Results

Trends of production with age and environmental variables

Figure 2 shows scatter plots of both GPP and NPP against forest age for the data available here. Logarithmic transformations have been used because the data were otherwise spread too widely on either axis to be viewed reasonably. Even then, it is clear that there is much variation in both GPP and NPP at any one age; this is unsurprising given the wide geographic scatter, range of forest types and variety of environmental circumstances that were included in the data.

Table 1 For the data set used here, the number of sites in various climatic regions and the numbers of observations and minimum-mean-maximum values of various characteristics of those Annual precipitation Values (mm) 257-670-1866 294-1311-2724 1649-2064-3072 257-1161-3072 No. of ob. 51 125 7 183 Mean annual temperature Values (°C) 1.2-4.3-6.9 5.1-8.8-15.3 25.7-26.1-26.6 1.2-8.8-26.6 No. of ob. 27 162 No. of ob. Values (g C m -2 year -1 ) 39-237-517 214-645-1720 128 7 900-1230-1560 39-590-1720 NPP 15 73 2 90 734-1533-3440 No. of ob. Values (g C m -2 year -1 ) 559-1007-1845 3000-3468-4038 559-1430-4038 GPP 133 287 13 433 Ages of measurement (year) 22-89-350 20-86-795 21-137-500 20-88-795 Soft-wood Unspecified b No. of sites 46 88 6 Number of sites of various forest types 140 c 9 9 3 21 25 53 - 78 3 12 Hard-wood 41 sites Climate a Cold Temperate 26 Tropical All No. of Ob. is the number of observations a Climate classifi cation is based on that of Reich and Eswaran ( 2002). Temperate refers generally to sites in the latitudinal range 22-55° N or S, cold to regions N or S, respectively, of the temperate regions, and tropical refers to the remaining equatorial regions b For many sites, Campioli et al. ( 2015) specified only that it was forest, not what type of forest c The actual number of sites in the data set of DeLucia et al. ( 2007) was uncertain

Fig. 2 Scatter plots of the natural logarithm [ln()] of GPP (filled circle) and NPP (open circle) against the natural logarithm of forest age for the data used here. The solid lines show how predicted values of GPP vary with age at sites with each of three mean annual temperatures as determined using Eq. ( 4). The dashed lines show similar predictions of NPP using Eq. ( 5). P was productivity (GPP or NPP, g C m -2 year -1 ), and A was forest age (year)

In their analysis of the largest part of the present data set, Luyssaert et al. ( 2007) showed in their Figs. 3 and 4 that both GPP and NPP tended to increase with the mean annual temperature of the site on which the forest was growing and with the annual precipitation. The scatter plots in Fig. 3 from the present data illustrate this clearly and suggest that the relationship between the logarithms of both GPP and NPP and the logarithms of either of those environmental variables is linear. The relationships appear to be quite strong in the case of mean annual temperature ( r 2 = 0.50 and 0.85 for GPP and NPP, respectively), but rather less sofor precipitation ( r 2 = 0.08 and 0.53).

Regression relationships

The next step in the analysis was to attempt to developregression relationships of GPP and NPP with mean annual temperature, precipitation and forest age. In doing so, account was taken of the fact that many of the sites in the data set had numerous measurements of GPP or NPP taken at different ages. In regression analysis, these multiple measurements from the individual sampling units (the sites) lead to under-estimation of the covariance matrix of the parameter estimates and over-estimation of the r 2 value of the fitted model (West et al. 1984). Using techniques of multiple linear regression analysis that allow for this (West 1995), it appeared that once the relationship between productivity (GPP or NPP) and mean annual temperature had been established, there was no advantage gained by adding annual precipitation to the relationship. Thus, it appeared that a suitable model to be fitted was:

Fig. 3 Scatter plots of the natural logarithm of GPP (filled circle) and NPP (open circle) against the natural logarithms of a mean annual temperature and b annual precipitation for the data available here. The lines drawn are the ordinary least-squares straight-line fits to the data in each case for GPP (solid lines) and NPP (dashed lines). P was productivity (GPP or NPP, g C m -2 year -1 ), T was temperature (°C), and p was precipitation (mm)

where P was productivity (GPP or NPP, g C m -2 year -1 ), A was forest age (year), T was mean annual temperature (°C), and a, b and c were parameters to be estimated.

After further consideration of the data, there was found to be no appreciable gain from the inclusion of the term in age in the model for GPP. Thus, the model fitted in that case may be written as:

Note that this includes multiplication by the correction factor espoused by Snowdon ( 1991) (the mean of the untransformed observed values divided by the mean of the back-transformed fitted values from the regression, calculated here as 1.03) to allow for bias in estimates of GPP from the model due to the back-transformation from logarithms of Eq. ( 3). The r 2 value of this model (in Eq. 3) was 0.49. Adding the term in age to this increased that value by ＜ 0.01.

For NPP, the model fitted included age and was:This also incorporates multiplication by a bias correction factor of 1.02. The r 2 value of this model was 0.92, an increase over the value of 0.88 when the term in age was excluded.

Superimposed on Fig. 2 are lines drawn to show how these relationships predict the change with age of both GPP and NPP for sites with each of three different mean annual temperatures. The lack of a trend with age for GPP and the decline with age for NPP are both of considerable interest and will be discussed in more detail below.

Discussion

Factors determining G PP and NPP

Climatic f actors

Both GPP and NPP increased as mean annual temperature increased and to a lesser extent as annual precipitation increased (Fig. 3). The models fitted to quantify these relationships (Eqs. 4, 5) included temperature only and the addition of annual precipitation did not appear to improve the fit to the data appreciably. This is consistent with the view of Malhi et al. ( 1999), who, in their overview of global carbon balance of forests, concluded (p. 716) that “[t]he primary cause for [the] difference [in forest growth] is temperature, which at high latitudes limits the growing season, and restricts decomposition and nutrient recycling, but at low latitudes encourages rapid decomposition of soil organic matter and rapid recycling of nutrients into vegetation growth.” Of course, at regional scales, water availability may be a more important determinant of growth than temperature (e.g. Yue et al. 2018).

By contrast with these findings, Michaletz et al. ( 2014) made the rather extraordinary claim that climate, through mean annual temperature and precipitation, did not infl uence NPP directly but rather that forest biomass did. It is argued in Supplementary Appendix B that the model system they used described net biomass growth (defined at Eq. A.4 in Supplementary Appendix A), rather than NPP, in relation to annual temperature and precipitation. It is concluded that that their results are completely consistent with the findings of the present work that mean annual temperature and precipitation are direct determinants of plant growth that determine size, rather than size determining growth, although size and growth are generally positively correlated (Litton et al. 2007; Sillett et al. 2010).

It is apparent alsofrom the results of Figs. 2 and 3 that autotrophic respiration (the difference between GPP and NPP, see Eq. 1) tends to be greater on sites with a lower temperature regime. This suggests that the nature and extent of the metabolic processes that are necessary to maintain tree life differ somewhat in response to the temperature regime of a site.

Forest a ge

The present results suggest that once climatic infl uences have been allowed for, GPP was unaffected by age whilst NPP declined progressively (Fig. 2). In an early analysis of their data set, Luyssaert et al. ( 2008) found suggestions that NPP declined with age, consistent with the present results. However, the finding here that GPP did not change with forest age is in direct contradiction to the results of Tang et al. ( 2014) who also used the data of Luyssaert et al. ( 2007). They concluded that GPP (and NPP) increased progressively at younger ages reaching a maximum somewhere within the range of 50-100 years and declined thereafter. In Supplementary Appendix C it is argued that their finding was an inevitable conclusion of their analysis method, which would show a decline at later ages whether it actually existed or not in the data.

In two other global forest data sets, NPP has been found declining with age (Pregitzer and Euskirchen 2004; Michaletz et al. 2014). Some additional data sets, which did not have such a wide geographic spread as the global data sets considered here nor had accompanying environmental data, are shown in Fig. 4. GPP appeared to be unrelated to age in any one of those data sets whilst NPP appeared to decline. Xu et al. ( 2012) used a model-based method, that was based on chamber measurements of photosynthesis, to estimate GPP in a chronosequence (plots aged 35, 70, 90 and 135 years) of oak ( Quercus) dominated forests in northeastern USA and concluded that GPP was little changed with age.

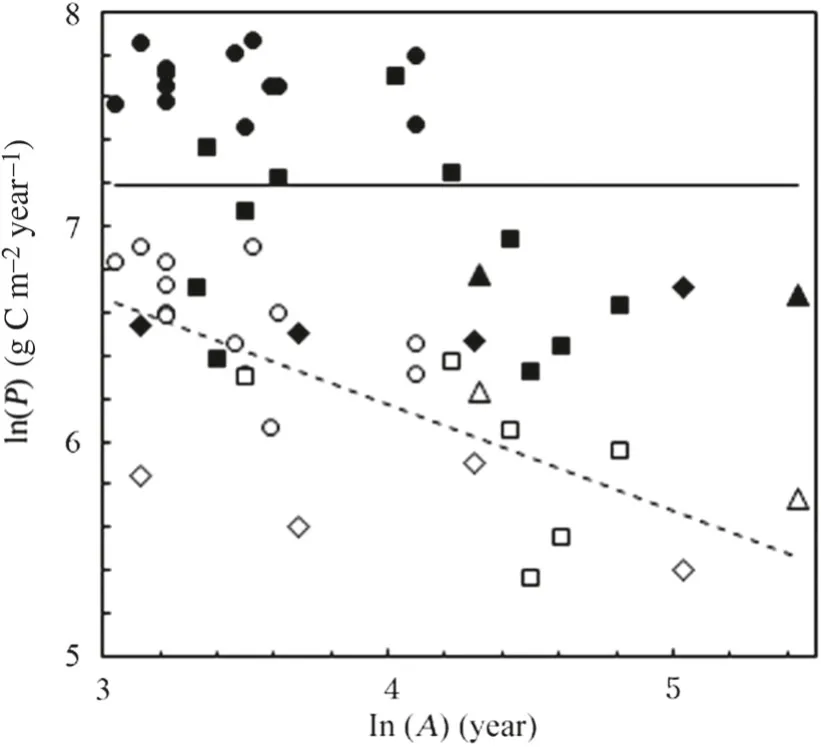
Fig. 4 Scatter plots of natural logarithms of GPP (solid symbols) and NPP (open symbols) against natural logarithms of forest age from (filled circle, open circle) a chronosequence of nine stands aged 4-60 years of Veitch’s fir ( Abies veitchii Lindley) growing on the slopes of Mt Fuji, Japan (Tadaki et al. 1970; Ogawa 2009), (filled diamond, open diamond) a chronosequence of four stands aged 23-154 years of various successional stages in mixed conifer-hardwood stands of the boreal regions of Canada (Goulden et al. 2011), (filled square, open square) 11 stands aged 23-123 years of managed boreal and temperate hardwood and softwood forests in Canada (Zha et al. 2013) and (filled triangle, open triangle) two woodland stands of Faber’s fir ( Abies fabri (Mast.) Craib) on the Tibetan plateau (Shu et al. 2019). There was no evidence of a trend with age of GPP in any of these data sets; the solid line indicates their overall mean GPP. NPP tended generally to show a decline with age and the dashed line shows the ordinary least-squares fit to the combined data as NPP = 3513 A -0.497 , where A was age (year)

It is perhaps important to appreciate that to determine properly whether or not GPP and NPP actually change with age at any one site would require that repeated measurements be made over an extended time period at that site (e.g. Litton et al. 2007). Even then, year to year variations in climatic conditions will aff ect growth rates and may tend to confound age effects. Use of chronosequences of one forest type across a set of geographically nearby and otherwise similar sites may assist in this respect; they allow that growth rates at different ages under the same climatic circumstances be compared. For the present work, data were obtained from sites with both a wide geographic scatter and range of environmental circumstances. At least some of the site variation effects on growth rates could then be removed by relating them to site climatic characteristics. effects of different forest types and other site Differences inherent in the data set are then refl ected in the unexplained variation when fitting the data to Eqs. ( 4) and ( 5). Thus, the results obtained here suggest simply that GPP did not vary with forest age whilst NPP tended to be lower in older forests. However, it has then been inferred here that this reflects a tendency at any one site for GPP to be unaffected by age and for NPP to decline.

How may GPpremain unchanged with age?

The most preferred explanation in the past for the decline of NPP with age has been that it is a consequence of a decline with age in GPP, as suggested by the hydraulic limitation theory (Ryan and Yoder 1997). In their major review of the theory, Ryan et al. ( 2006) summarized results from 51 studies of older and younger trees that had measured some or all of water potential, stomatal conductance and photosynthetic capacity in shoots taken at increasing heights in individual trees or at assorted positions within the forest canopy. These studies had used chamber techniques principally to make their measurements; such studies have continued subsequently (e.g. Greenwood et al. 2008; Nabeshima and Hiura 2008; Abdul-Hamid and Mencuccini 2009; Ambrose et al. 2009, 2010; Renninger et al. 2009; Drake et al. 2010; Räim et al. 2012; Asao et al. 2015; Pangle et al. 2015; Azuma et al. 2019). Many, but by no means all, of these studies showed declines with increasing height in individual trees of these three measured characteristics. Furthermore, these effects varied seasonally and with different positions in the tree crown. Where these phenomena have been observed, it has been implied that if the photosynthetic capacity of individual trees in a stand has been reduced from time to time during a year, this will lead to a reduction in GPP of the whole stand when individual tree photosynthetic amounts are summed over a whole year and the whole stand.

However, many of the studies reviewed by Ryan et al. ( 2006) suggested that trees can make plastic changes with age in the morphology and anatomy of newly developing tissues as they grow. These changes may help to compensate for the loss of photosynthetic capacity over the whole canopy in response to increased water stress, whether this be due to increasing tree height with age or reduced water availability from the soil. Studies identifying such changes have continued subsequently (Martínez-Vilalta et al. 2007, 2009; Greenwood et al. 2008; Ishii et al. 2008, 2014; Nabeshima and Hiura 2008; Abdul-Hamid and Mencuccini 2009; Ambrose et al. 2009, 2010; Renninger et al. 2009; Sterck and Schieving 2011; Räim et al. 2012; Hölttä et al. 2013; Coble et al. 2014; Asao et al. 2015; Binks et al. 2016a, b; Zhang et al. 2016; Coble and Cavaleri 2014, 2017; Buckley et al. 2017; Kiorapostolou et al. 2018; Prendin et al. 2018; Azuma et al. 2019). Variation with height in the tree of xylem, phloem and leaf properties has been inferred as contributing to these compensatory mechanisms. Also mentioned are reductions in leaf water potential during the hottest time of day and increased capacitance of leaf tissue to store water to alleviate water stress. All these changes are consistent with maintenance of the photosynthetic capacity of leaves by ensuring water availability to them. In canopies of trees of varying age and height of ponderosa pine ( Pinus ponderosa Dougl. ex. Laws.) in Montana, Sala and Hoch ( 2009) found the amounts of non-structural carbohydrates (in essence the products of photosynthesis) increasing despite increasing water stress in the upper reaches of the canopies of taller trees; this illustrated how effective these compensatory mechanisms seem to be.

With respect to xylem characteristics in this context, two issues apply. The lumen diameter of the xylem cells in any one tree ring (tracheids in gymnosperms and vessels in angiosperms) increases from the tree tip towards the base of the stem (Mencuccini et al. 2007; Anfodillo et al. 2013; Carrer et al. 2015). The degree of taper down the stem (and length of tracheids in conifers) aff ects the conductivity to water of the conduits and may then infl uence the photosynthetic capacity of the leaves to which they are supplying water (Mencuccini et al. 1997; Mencuccini 2002; Zaehle 2005; Petit et al. 2008; Taylor and Eamus 2008). However, the thickness of the cell wall of all xylem elements (vessels, tracheids and fi bres) may differ also as cells develop and this, together with their lumen diameter, determines the basic density of wood (oven-dry weight per unit volume of undried wood) at any point in the stem (Santini et al. 2012; Martínez-Cabrera et al. 2012; Ziemińska et al. 2013; Fortunel et al. 2014; Lachenbruch and McCulloh 2014; Dadzie et al. 2016; De Micco et al. 2016; Luostarinen et al. 2017; Osazuwa-Peters et al. 2017; De Mil et al. 2018; Dlouhá et al. 2018).

Basic density correlates closely with wood strength and stiffness which determine if the stem is suffi ciently strong to carry out its other primary function of carrying the leaves and branches high in the air. Detailed studies within the genus Eucalyptus have shown that the stem wood of species that occur naturally in more arid climates display smaller vessel lumen diameters, a higher density per unit area of vessels and reduced sapwood conductivity, all characteristics that appear to be adaptations to water stress consistent with the site conditions on which they occur (Pfautsch et al. 2016;. Saadaoui et al. 2017). However in the coniferous species jack pine ( Pinus banksiana Lamb.) in Canada, lumen diameter and sapwood conductivity were found to increase with tree age (Pothier et al. 1989a, b) whilst in the mountain ash ( Eucalyptus regnans F. Muell.) in southern Australia, sapwood conductivity appeared to be increased at greater heights up the stem (West and Wells 1990). These latter results for particular species on particular sites are consistent with the view that lumen diameter of developing stem wood cells may be expected to increase in response to water stress to increase sapwood conductivity and maintain water supply to leaves. At the same time as lumen diameter changes, cell wall thickness will be determined in response to stem strength requirements. Thus sapwood cross sectional area at height in the tree stem will be determined by a balance between these two requirements. It has been found that strength and conductivity may be correlated (Mencuccini et al. 1997; Barotto et al. 2017, 2018; Rungwattana and Hietz 2018).

In the present context, Ryan et al. ( 2006) referred to reports of decreases with tree height in the ratio of the leaf area held above some height to the sapwood area in the stem at that height, sapwood through which water must pass to supply those leaves; such a decrease implies that the conductivity of sapwood to water movement has increased so affording some alleviation of water stress in leaves above that height. However, other reports have shown leaf area/sapwood area ratios increasing with height (Phillips et al. 2003; Buckley and Roberts 2006; Simonin et al. 2006; Ambrose et al. 2010). The present discussion has suggested that sapwood area at any height in the tree stem reflects a compromise between water conductivity and stem strength requirements. Thus, it might be expected that the way the leaf area/sapwood ratio varies with height might differ for different species whilst still allowing sapwood conductivity to increase in response to a need to maintain water supply to leaves high in the canopy; this may then be part of the compensatory mechanism to ensure the maintenance of photosynthetic capacity of the canopy.

As well as plastic changes in xylem anatomy, substantial changes can occur in the morphology and anatomy of newly developing leaves. The extraordinarily detailed work of Chin and Sillett ( 2017) illustrates the complexity of these changes. They sampled leaves at many heights by climbing a number of 85-100 m tall Sitka spruce ( Picea sitchensis (Bong.) Carr.) trees in old growth forest in northern California; Sitka spruce is one of the tallest tree species in the world. They measured over 40 morphological and anatomical macro- and micro-scopic characteristics of the leaves. In particular, they found that leaf mass area (the oven-dry biomass of a leaf divided by its surface area, the reciprocal of which is commonly termed Specific leaf area) increased with height; increased leaf mass area is generally associated with reduced short-term photosynthetic capacity of leaves but with a longer leaf lifespan that may eventually provide greater long-term photosynthetic production per leaf (Niinemets 1999b, 2001; Wright et al. 2004; Miyashita and Tateno 2014). They found also that leaf length was reduced at greater heights, probably due to restrictions on cell elongation as a consequence of increased water stress. There were substantial changes also at different heights in leaf microscopic structures including stomatal positioning and mesophyll structure, changes that might aff ect stomatal conductance or hydraulic conductivity. They concluded that the light availability effects on plasticity of leaf structure were rather more substantial than the water stress effects and that leaf photosynthetic capacities would change in response to these plastic modifi cations.

Similar studies were carried out in redwood ( Sequoia sempervirens (D. Don) Endl.) forests of California (Oldham et al. 2010); redwood includes the tallest trees in the world and frequently occurs in association with Sitka spruce. Leaves at the top of redwood trees were shorter and had higher leaf mass area than those further down, as was the case for Sitka spruce. However, those characteristics seemed to be associated with increasing water stress at greater height in redwood, rather than with light availability as was the case for Sitka spruce. The extent of these plastic changes in both internal and external leaf structures at different heights in redwoods are evident from the microscopic leaf cross sections reproduced from Oldham et al. ( 2010) and shown in Fig. 5.

Fig. 5 Microscopic cross sections of leaves of redwoods in California USA, collected from a 110 m and b 48 m above ground: s cale ba r = 0.2 m m. From Fig. 5 of Oldham et al. ( 2010), reproduced by kind permission of the American Journal of Botany © 2010 The Botanical Society of America

There are many other reports from a wide range of tree species of substantial plastic changes in developing leaves in response to the environmental circumstances under which the trees developed or changes in light availability and/or water stress at different heights in the forest canopy. Characteristics such as leaf size, shape, venation, petiole thickness and leaf mass area, stomatal characteristics, cellular type and arrangement, leaf arrangement on shoots and shoot structure have all been found to vary substantially (Schoettle 1994; Niinemets 1999b, 2001; Niinemets and Kull 1999; Niinemets et al. 1999, 2005; Niklas 1999; Richardson et al. 2000; Greenwood et al. 2008; Ambrose et al. 2009; Räim et al. 2012; Coble et al. 2014; Ishii et al. 2014; Osada et al. 2014; Azuma et al. 2016; Binks et al. 2016a, b; Fellner et al. 2016; Coble and Cavaleri 2014, 2017; Jankowski et al. 2017; de la Riva et al. 2018; Domingues et al. 2018; He et al. 2018; Kawai and Okada 2018; Kiorapostolou et al. 2018; Kuusk et al. 2018a, b; Zhang et al. 2018a, b). In many of these papers, it is argued that these changes are consistent with compensatory mechanisms to maintain photosynthetic capacity of the canopy. Hardiman et al. ( 2013) even found that the spatial heterogeneity of foliage distribution within the canopy of a chronosequence of mixed hardwood-softwood forest in Michigan, USA aff ected the efficiency with which light and nitrogen were used, at least in determining aboveground NPP. Reviews are available describing how variations in morphology of, and anatomical structure within, leaves of many plants, trees and others, can aff ect their photosynthetic capabilities (Evans 1999; Garnier et al. 1999).

Turgor (the cytoplasmic pressure within cells) of buds and leaves is an important determinant of the ability of cells to increase their size, hence for buds to swell, leaves to expand and branches to elongate. Leaf turgor, as well as water potential, was found to decline with height in tall redwoods (Koch et al. 2004) and Douglas-fir ( Pseudotsuga menziesii (Mirb.) Franco) (Woodruff et al. 2004) and this probably explains the reduced leaf lengths at greater heights in Sitka spruce and redwoods mentioned above (Oldham et al. 2010; Chin and Sillett 2017). In both redwood (Ishii et al. 2014) and Japanese cedar ( Cryptomeria japonica D. Don) (Azuma et al. 2016), reduced leaf turgor was associated with increased ability of leaves to store water. Thus, cell turgor effects appear to be part of the hydraulic limitation theory and may be part of compensatory mechanisms to maintain leaf photosynthetic capacity.

Through all these studies, it appears that in response to increasing water stress near their tops and/or reducing light availability lower in the crown, trees are often able to make plastic adjustments in the morphology and anatomy of newly developing xylem and leaf tissues. These changes may then compensate for reduced leaf photosynthetic capacity in response to these stresses allowing photosynthetic capacity over the entire forest canopy to be maintained as trees become older and taller. The limitations imposed by these water stresses eventually lead to a slowing of tree height growth at older ages whilst stem diameter growth and, hence, biomass growth may continue (Phillips et al. 2008; Sillett et al. 2010).

Autotrophic respiration

As is evident from Eq. ( 1), the only difference between GPP and NPP is autotrophic respiration. Thus, if GPP is unchanged with age, energy requiring metabolic activity must increase progressively with age so that increased autotrophic respiration becomes the cause of the decline in NPP. This rules out the hydraulic limitation theory; the compensatory processes trees may undertake to maintain their photosynthetic capability in the face of hydraulic limitation were discussed in the preceding section.

Over the years there have been at least five suggestions as to what progressively increasing sources of respiratory loss might contribute to the decline. These losses would occur in individual trees and would sum across all trees of the stand to lead to an overall reduction in autotrophic respiration of the whole stand. Whilst none might be suffi cient to explain completely the decline of NPP, each might contribute more or less to the decline and, when considered together, they might be suffi cient to explain it fully. The five suggestions are for increased respiratory losses

· Required to maintain an increasing live tissue biomass within wood as trees grow taller and larger (Yoda et al. 1965),

· Involved with construction and maintenance of more complex morphologically and/or anatomically structured tissues in response to reduced light availability and/or increased water stress (Reich et al. 1998; Niinemets 1999a; Niinemets and Kull 1999; Rowland et al. 2015),

· With increased turnover rates of fine roots in older forests (Magnani et al. 2000),

· Incurred in the transport of carbohydrates and hormones through an increasing length of phloem as trees grow taller (Penning de Vries 1975a, p. 461; Kramer and Kozlowski 1979, p. 611),

· From smaller, competitively unsuccessful trees or from taller trees subject to hydraulic limitation (Binkley et al. 2002, 2006; Binkley 2004).

Each of these five possibilities is discussed in a sub-section below.

Increased amounts of tissue as trees grow

The progressively increasing respiration needed to maintain a progressively increasing amount of live tissue in a stand of trees as it ages has been the only source of increased respiration with age that was considered in some detail for possible involvement in the decline of NPP with age. However, it seemed clear that it was insufficient to explain the decline (Ryan and Waring 1992; Ryan et al. 1997) and the hydraulic limitation theory became the preferred hypothesis.

Unless there is a dramatic change in environmental circumstances (e.g. reduced water or nutrient availability), leaf and fine root biomass of a stand tends to remain more or less unchanged with age, whilst sapwood volume increases progressively as trees increase their size. Mencuccini and Grace ( 1996, Fig. 3) found sapwood volume in stems increasing progressively with stem diameters in a 7-60-year chronosequence of Scots pine ( Pinus sylvestris L.) in the UK. Sapwood contains live parenchyma tissue that constitutes 10-25% of its volume in angiosperms and somewhat less in gymnosperms (Spicer 2014, Table 1); small amounts, with specialized functions, may even exist in heartwood of some species (Celedon and Bohlmann 2018). Meir and Grace ( 2002) found that stem respiration of trees in some African and Brazilian rainforests increased substantially with increasing stem diameter. It was about four times greater in a stem section with a diameter of 100 cm than in one with a diameter of 10 cm (derived from their Fig. 3). If sapwood volume or respiration increase with increasing tree diameter (hence biomass) in a stand at any particular age, it seems reasonable to suggest that they will increase further as the trees become larger with age and their total summed across all trees in the stand will increase with age. Phloem tissue has a much smaller overall volume than sapwood, but it seems to be completely replaced annually (Hölttä et al. 2013); as trees grow taller with age, it will increase in its total volume so incurring increasing construction and maintenance respiratory costs.

The present results (Eqs. 4, 5) suggest that total autotrophic respiration over a forest stand, growing at a mean annual temperature of 15 °C, constitutes about 40% of GPP at 20 years of age and this becomes about 60% at 200 years of age. The proportions are much higher, 80% becoming 90%, at the much lower mean annual temperature of 2 °C. For live stem tissue in particular, a number of reports have suggested its maintenance respiration varies considerably between different forest types; values have been reported ranging over 5-50% of GPP (Ryan et al. 1994, 1997; Law et al. 1999; Meir and Grace 2002). Some of this variation no doubt reflects the different forest types being considered, their different ages and the different temperature environments under which they were growing. However, the overall implication is that stem maintenance respiration constitutes only a modest part of total autotrophic respiration. It was recognition of this that was an important element of the earlier conclusion that increases in stem respiration were insufficient to explain the decline of NPP with age. However, in the present context, it seems reasonable to suggest that such an increase with age may play at least some part in the decline, though certainly not all. It can also be expected that live coarse root sapwood tissue will increase as coarse root systems enlarge to ensure ever larger trees can remain firmly anchored within the soil (e.g. Stokes et al. 1995, 1997; Nicoll and Ray 1996; Tamasi et al. 2005; Nicoll et al. 2006, 2008).

Not only will the length of live tissue to be maintained in stem and coarse root sapwood increase as trees grow taller, but so too will that of the dead tissue that make up the wood in both sapwood and heartwood. The biomass of that additional tissue will be part of the NPP of the tree. However, the metabolic cost of conversion of sapwood to heartwood (Song et al. 2014; Sillett et al. 2015; Celedon and Bohlmann 2018; Chen et al. 2018) will increase respiratory costs with age because they will apply over an ever-increasing length and area of those tissues. Sillett et al. ( 2010) found that the proportion of individual tree biomass growth involved in heartwood production increased with age of trees of redwood in California and mountain ash in Victoria, Australia, the softwood and hardwood species, respectively, that grow to the tallest heights in the world. It may be inferred that this will mean increasing respiratory costs with age are involved in sapwood to heartwood conversion in these species.

Construction and maintenance respiration of increasingly complex tissue

The construction of new tissue during plant growth and development involves a “cost” to the plant. This cost is considered to be made up of both the biomass of the new tissue (that is part of NPP) and the metabolic energy required in its construction that determines construction respiration (Eq. 2). Various methods have been used to determine “construction cost” and these are summarized in Supplementary Appendix D.

In earlier discussion, much attention was paid to the fact that morphology and anatomy of various newly developing tissues may undergo substantial modifi cation in response to changing light and water stress circumstances within the canopy of taller, older trees; of course, these changes will continue only until these circumstances limit height growth itself (Phillips et al. 2008; Sillett et al. 2010). It is assumed generally that there will be an increased construction cost involved in the development of these more complextissue. Leaf construction costs seem to have received particular attention in this context. Merino et al. ( 1984) proposed that leaf construction costs refl ect the environmental circumstances of the species concerned; they suggested that this might be a consequence of particular chemical constituent needs, such as the need for higher concentrations of certain lipids as defense against drought in arid climates. Griffin ( 1994) summarized a number of studies of leaf construction costs that found light and water availability aff ecting them. Saenger and West ( 2016) found leaf construction costs in a number of species of Australian mangroves tending to be higher the more complex their anatomical structure. Niinemets ( 1999a) found increased construction costs with increases of leaf mass area due to increased water stress higher in the canopy of temperate hardwood forests in Estonia. Nagel et al. ( 2002, Fig. 4) found higher construction costs associated with leaves with higher photosynthetic capacity in mixed hardwood forests in New York, USA. Rapidly growing, invasive species in Hawaii, USA with leaves with short-term high photosynthetic capability had lower costs than native species that had leaves with longer-term high photosynthetic capability (Baruch and Goldstein 1999).

In the context of the present work, it is the respiratory part of the construction cost that is of interest. If increased construction respiration of more complex developing tissues of taller, older trees contributes appreciably to the decline in NPP with age, there needs to be some indication that it can be an appreciable proportion of total autotrophic respiration.Table 2 lists some results from a number of tree species from various parts of the world. Those results, albeit principally for stems and whole trees, suggest that construction respiration is often of the order of 20-30% of total respiration, at least during the growing season. Of course the total construction respiration for any tissue will be the product of the length of time over which construction occurs, the biomass of the tissue being newly constructed and the rate of construction respiration per unit biomass constructed. That will then determine its total contribution to autotrophic respiration over a year and, hence, its possible effect on NPP. Much work is required to quantify these amounts for different tissues and forest types. However, the implication from these results is that if changes in tissue morphology and anatomy in response to stress of one sort or another do lead to increases in construction respiration costs of the tissues, the effects might be appreciable.

It is inviting to suggest that construction respiratory costs will increase progressively with age as trees grow and require increasing degrees of plastic tissue modifi cation. The methods to determine construction cost of tissues (see Supplementary Appendix D) have assumed that those costs are determined by processes that take place close to the construction site; the architects of one of these methods (Penning de Vries et al. 1974, p. 360) referred to scales of centimeters and assumed that transport costs of materials over those distances during construction were negligible. However, it seems reasonable to assume that other processes, perhaps hormone mediated or involving additional metabolic demands for nutrient uptake from the soil, are involved in controlling the complex changes necessary to adjust leaf photosynthetic capacity and cell sizes and their arrangement within tissue (such as those shown in Fig. 5). Penning de Vries et al. ( 1974, p. 361) recognized the presence of substances such as hormones in newly constructed tissues, but they and their role in construction were not included as part of their method to determine construction costs. No doubt, the metabolism involved with those controlling processes would incur respiratory losses perhaps many metres from the construction site, at the tip of the tree or the end of the root system. Certainly effects on xylem cell diameter and taper, mentioned earlier, must apply throughout the length of the vascular tissue. Thus, they may apply over distance of many tens of metres and are believed to be aff ected by hormones (Aloni 2013; Hacke et al. 2017). Such long-distance effects may increase construction respiration costs and seem to have been little considered to date.

Once construction of new tissue is complete, it will incur maintenance respiration costs for as long as it remains alive; methods to determine such costs are discussed in Supplementary Appendix D. It may be that more complexly structured tissue requires a higher level of maintenance respiration, which may again increase the overall respiration load of larger, older trees. Limited work seems to have investigated such a possibility. Reich et al. ( 1998) used chamber techniques to measure respiration of fully developed leaves from fully sunlit parts of the crown of a large number of species from forests ranging from alpine tundra to the tropics. They found that maintenance respiration tended to be higher in leaves that had a reduced long-term photosynthetic capability (higher light saturated photosynthetic rate, but a shorter lifespan and lower leaf mass area). Rowland et al. ( 2015) used chamber techniques to measure leaf maintenance respiration of sunlit leaves near the top of the canopy of 11 tree species in the Amazonian rainforest in an experiment where 50% of rainfall had been excluded for 13 years or not. Where rainfall had been excluded, respiration rate averaged 28% higher than where it had not and was 49% higher in more drought sensitive species. In their words, these increases “likely refl ect[s] the need for additional metabolic support required for stress-related repair, and hydraulic or osmotic maintenance processes”.

Table 2 Estimates for various species and various tree parts of the proportion of total respiration that was construction respiration over the growth period specified

Fine root system development

Fine roots are defined generally as live roots with diameters in the range 1-5 mm. Averaged over forests globally, they make up about 5% of the forest total biomass, whilst about 75% is in above-ground tree parts and 20% is in coarse roots (Brunner and Godbold 2007). A number of studies of fine root biomass across forest chronosequences, for both hardwood and softwood forests in various parts of the world and covering ages from 4 to 178 years, suggest that biomass development with age of fine roots is similar to that of foliage. It increases rapidly during early stand development, reaching a maximum as the canopy reaches full development, and then declines and stays more or less constant thereafter to advanced ages (Vanninen and Mäkelä 1999; Makkonen and Helmisaari 2001; Claus and George 2005; Fujimaki et al. 2007; Børja et al. 2008; Schoonmaker et al. 2016).

Despite their rather small proportion of total biomass, annual fine root production can be very substantial. Based on global data sets from a wide range of forest types around the world, fine root annual production constituted about 30% of the total NPP of the forest (Jackson et al. 1997; Noguchi et al. 2007) and perhaps 40-50% of above-ground NPP (Nadelhoffer and Raich 1992). Part of the reason for this large rate of production is that the lifespan of fine roots is often somewhat shorter than that of leaves. Using a global data set, Gill and Jackson ( 2000) determined that their average lifespan increased progressively from about 1 to 2.6 years as the mean annual temperature of the site on which the forest was growing increased from 0 to 30 °C. Of course fully deciduous trees must replace all their leaves annually and so it may be expected that respiratory costs associated with leaf replacement in those cases may be appreciably greater than for evergreen species. However, the overall implication is that respiratory costs associated with fine root production may constitute an appreciable proportion of total autotrophic respiration, a proportion that will vary appreciably as forest circumstances differ.

Magnani et al. ( 2000) proposed a variation on the hydraulic limitation theory as an explanation for the decline of NPP with age. In response to the increasing water stress in the foliage of trees as they grow taller, they suggested there may be a shift towards fine root development with a decline in their lifespan, perhaps coupled with changes in sapwood conductivity, to maintain the water balance within the foliage; this would be part of the compensatory mechanism by trees to maintain photosynthetic capacity as discussed earlier. An increased turnover rate of fine roots would be accompanied by increased respiratory losses that could then contribute to the decline with age in NPP. Magnani et al. developed a model system based on these concepts and showed it could explain the growth behavior of a 7-59 years chronosequence of Scots pine in the UK. Other chronosequence studies of various species in various parts of the world have found a decline in fine root lifespan with age, consistent with this model, (Chen et al. 2016; Krasowski et al. 2018) whilst some have not (Andersen et al. 2008; Chen et al. 2016), suggesting this phenomenon may not apply universally but only in some species.

There have been suggestions also that fine root system morphology might change with age. In a chronosequence of 19 lodgepole pine ( Pinus contorta Loudon) stands in Canada, aged 12, 21, 53 or ≥ 100 years, fine roots and leaves tended to become thicker (greater root mass length, root mass area and leaf mass area) between 53 and 100 years of age (Schoonmaker et al. 2016). In a chronosequence of five 6-90 year old plantation sites of Japanese cedar in Japan, Hishi et al. ( 2017) alsofound morphological changes in fine roots. Their results suggested that more highly functional root tips, with higher maintenance respiration costs and a reduced lifespan were developing with age; Ugawa et al. ( 2018) found evidence that similar effects may occur in native fir forests (dominated by Marie’s fir, Abies mariessi Masters and Veitch’s fir, A. veitchii Lindl.) of sub-alpine Japan. Such changes are consistent with the possible effects on respiratory rates of the morphological and anatomical changes of leaf and vascular tissues to compensate for reduced photosynthetic capacity as discussed earlier. Furthermore, root system development is controlled substantially by hormonal function (Hodge et al. 2009) and respiratory requirements for that metabolism must be considered also.

Respiratory losses through phloem transport

The mechanism of phloem transport in trees has been discussed in numerous reviews (Thompson and Holbrook 2004; Minchin and Lacointe 2005; Van Bel 2003; Lacointe and Minchin 2008; Knoblauch and Peters 2010; De Schepper et al. 2013; Lemoine et al. 2013; Savage et al. 2016). In summary, the process is as follows. Solute (mainly sucrose) from the photosynthetic leaf parenchyma is transported to the sieve tube companion cell complex. This may be an active (requiring energy from respiration) or passive process; in most tree species it is passive. The sieve tube itself has a membrane that surrounds completely its internal circumference and extends along the entire length of the phloem conduit. Loading the solute into the sieve tube is then an active process. The higher solute concentration within the sieve tube leads to water movement from the sieve tube companion complex and/or the xylem. This leads to a higher pressure developing in the phloem conduit at the loading point; commonly, this is termed an “osmotic based hydrostatic pressure”. In response to the pressure gradient, mass flow of solute then occurs from the loading point along the conduit towards areas in the plant where it is needed. Thus, whilst loading of the phloem involves an active process, transport through it is passive.

As solute passes along the phloem, some may be unloaded here and there to provide tissues along the way with their metabolic needs or to be stored for later use. It is believed generally that unloading of solute is passive, probably assisted by “carrier” molecules to increase its speed. However, unloading of solute at any point is often excessive and some must then be reloaded for transport onward (De Schepper et al. 2013). Such reloading is active and, as the tree becomes taller and the phloem conduit becomes longer, this “leakage-retrieval” mechanism may incur increasing respiratory costs. Another suggestion as to how tree height might aff ect phloem transport cost was made by Sala and Hoch ( 2009), without supporting evidence, who said “…higher xylem tensions in the upper xylem and apoplast of tall trees could limit water movement from xylem to phloem (lower phloem pressure at source points), which could impose a bottleneck for photo-assimilate distribution…”.

Phloem physiology remains inadequately understood and so it is difficult to speculate as to what might be its contribution to overall respiratory costs. However, the discussion above does suggest that respiratory costs of phloem transport might increase as trees become taller, hence older.

Respiratory losses through stand development

The model of Binkley ( 2004) and Binkley et al. ( 2006) (termed here the Binkley et al. model) divides tree stand growth and development intofour phases. The first phase covers the period from the time that seedlings become large enough to utilize fully the resources for growth available from the site until a full canopy develops. During that period, NPP increases progressively with age. The present work concerns the subsequent three phases during which NPP declines with age.

The second phase commences as inter-tree competition starts after their canopies meet. Competition at this stage is “asymmetric” for light, when taller trees may shade smaller, but the reverse cannot occur (Hara 1986a, b; Weiner and Thomas 1986; West et al. 1989; Weiner 1990; Schwinning and Weiner 1998; Pretzsch and Biber 2010; del Río et al. 2014; West and Smith 2019). Growth of the shaded trees is suppressed and they contribute little to stand growth (Ford 1975; West 1980, 1981a, 1981b; West and Borough 1983; West and Osler 1995; Glencross et al. 2016), whilst growth is dominated by the bigger trees which tend to grow at rates disproportionately large relative to their sizes. The suppressed trees can do little photosynthesis, but must continue to respire if they are to survive (Korol et al. 1991); they show a low level of light use efficiency, that is, relatively little growth for the amount of light they intercept. Binkley et al. ( 2002) introduced the idea that this low level of light use efficiency could be considered part of the decline with age of NPP since maintenance respiration must continue as long as the trees stay alive. A number of studies have found light use efficiency reduced or respiration rates increased amongst smaller trees in the stand (Binkley et al. 2013; O’Grady et al. 2010; Fernández et al. 2011; Tschieder et al. 2012; Campoe et al. 2013; Gspaltl et al. 2013; Ex and Smith 2014; Gyenge and Fernández 2014).

Ferrio et al. ( 2018) studied growth, water use and respiration rates using the whole tree chamber methods of Mori et al. ( 2010) (discussed in the second section of Supplementary Appendix A) of young (7-10 years old) Japanese cedar trees that were in the second phase of the Binkley et al. model, growing in very dense stands (60,000 stems ha -1 ) so that the competitive interactions between taller and shorter trees would have been intense. They found that taller trees were more effi cient in water use than smaller, suggesting they were compensating for increasing water stress to maintain their photosynthetic capacity. Furthermore, their respiration rates per unit biomass of shoots and roots were reduced when compared to smaller trees consistent with the view that respiratory losses by smaller trees are relatively large for their size. These effects seemed quite clear even though the tallest trees they were considering were only 2.8 m in height.

However, such effects may vary between species Growth behaviour of individual trees of two eucalypt species, lemonscented gum ( Corymbia citriodora subsp. variegata (F. Muell.) A. R. Bean & M. W. McDonald) and Dunn’s white gum ( Eucalyptus dunnii Maiden), was compared at ages ranging over 8-14 year when both species were growing in monoculture in two experimental plantations in sub-tropical, eastern Australia (Glencross et al. 2016; West et al. 2016). Overall, stand basal area net growth was somewhat greater in the less shade tolerant species, Dunn’s white gum, than the more shade tolerant lemon-scented gum. Whilst groups of smaller, slower growing trees developed in stands of both species, those of the more shade tolerant species maintained their growth rates better than those of the less shade tolerant species. In the present context it seems reasonable to suggest that smaller trees of both species were less light use effi cient than larger, hence suff ering maintenance respiration losses relatively large for their size. However, the smaller trees of the more shade tolerant species would have suff ered even greater respiratory losses as they constructed more robust leaves, with a higher leaf mass area, as is usual in more shade tolerant species (Niinemets 2001, 2010; Lusk and Warton 2007). Ultimately, this may have provided those trees with suffi cient longer-term photosynthetic capacity to better maintain their growth rates when compared with smaller trees of the less shade tolerant species. But this would have been at the expense of reduced growth of the whole stand of the more shade tolerant species, through greater overall respiratory losses when compared with the less shade tolerant species.

Given these various considerations, it seems reasonable to suggest that respiratory losses by smaller and suppressed trees will contribute to the decline with age of NPP in the second phase of the Binkley et al. model. As time passes, smaller trees will die and so their overall contribution to this decline will vary from time to time as their numbers vary.

The third phase of the Binkley et al. model involves the transition to the fourth phase. By then, severely suppressed trees will have died and increased inter-tree spacing will mean the smaller trees then remaining will no longer be shaded to the same extent The one-sided, competitive intensity of larger trees over smaller will be much reduced. Such developments were discussed by West ( 2018).

A stand then enters the fourth phase of the model. This involves a reversal of growth dominance, where smaller, rather than bigger trees grow at rates disproportionately large relative to their sizes. There have been a number of reports of this occurring, but it has not always been the case (Binkley et al. 2003, 2006; Doi et al. 2010; Binkley and Kashian 2015; Baret et al. 2017, 2018). Binkley and Kashian ( 2015) made a number of suggestions as to how this growth reversal might arise. In the context of the present work and consistent with one of their suggestions, it is inviting to suggest that it might be a consequence of the greater water stress in their upper canopies to which taller trees in the stand are subject than is the case for shorter trees. To attempt to retain their photosynthetic capacity, this would require developing leaves (and/or xylem and fine root systems) of taller trees to undergo more substantial morphological and/or anatomical modifi cation, with concomitant increasing demands on construction and/or maintenance respiration, consistent with earlier discussion of changes made to compensate for reduced photosynthetic capacity. This would render taller trees less light use effi cient, so reducing their relative growth capacity in comparison with smaller.

Conclusion

This work was based on a data set of estimates of GPP and NPP from a wide range of forest types spread around the world with ages varying over the range 20-795 years. The analysis found that GPP and NPP increased as mean annual temperature of the site on which the forest was growing increased and this appeared to be a more important determinant of production than water availability. However, once Differences due to site mean annual temperature had been allowed for, there was no evidence that GPP changed with forest age whilst NPP progressively declined with increasing age, a decline that may be substantial (Fig. 2).

Consideration was given to what mechanisms might allow forests to maintain their GPP as trees become taller and older. Much argument in the past has revolved around measurements made of water relations taken from within the canopies of tall trees. This has shown that increasing hydraulic resistance to water movement from roots to leaves as trees grow taller leads to increasing water stress within the canopies. It has then been inviting to suggest that this would lead to reduced photosynthetic production by individual trees within a stand over any annual growth period and hence, when summed across all trees in the stand, to reduced GPP of the whole canopy. However, it has been found that as new leaves grow year by year, they undergo marked morphological and/or anatomical changes that allow compensatory photosynthetic processes to mitigate the effects on photosynthetic production of increasing water stress. Further, changes to both xylem structure and fine root structures and turnover rates have been identified that may act also as part of this compensation.

If GPP is unchanged with age, then the decline in NPP must be due to progressively increasing autotrophic respiration as that is the only difference between the two (Eq. 1). Attempts were made to itemize what the sources of those respiratory losses might be and why they might increase with forest age. Firstly, it was argued that as trees grow larger the amount of live tissue within the sapwood of stems and coarse roots will increase leading to an increasing respiratory cost to maintain them. Secondly, it was suggested that development of more complexly structured tissues, as mentioned in the previous paragraph, will require more complex metabolic processes that will incur increasing respiratory losses as trees become taller as they age. Other respiratory costs that might increase with forest age are those involved with the conversion of sapwood to heartwood as their total length or volumes increase, increasing transport costs of carbohydrates and hormones through the increasing length of the phloem and with increased turnover rate of fine roots. Also, growth ineffi ciencies of either very tall trees, that are unable to compensate fully for increasing water stress in canopies, or competitively unsuccessful small trees may also incur increased respiratory costs.

Attempts were made to outline the physiological circumstances that surround these possible sources of increased respiratory costs with forest age. However, it is not possible at this stage to identify exactly how much of the total autotrophic respiratory cost to the tree each of these sources might contribute. Further it is evident that their relative importance will differ from species to species. What is evident also is that the measurement of these sources of respiration is technically difficult (Cannell and Thornley 2000), both to identify the contribution by each to total respiration and to deal with the enormous size and difficulty of access of both the above- and below-ground parts of forest trees.

The present work was stimulated by a meta-analysis of a broad, global data set that suggested GPP does not vary with stand age whilst NPP is lower in older stands. As Binkley and Menyailo ( 2005) have pointed out, such an analysis is often just the first stage in a research project. It would be difficult to over-estimate the scope of the task that now remains to understand properly why forest growth rates decline with age.

AcknowledgementsI am extremely grateful to S Luyssaert of the VU University, Amsterdam for making available the data set he and his many colleagues compiled in 2007. Through him I thank all site investigators involved in collecting those data, their funding agencies, the various regional fl ux networks (Afrifl ux, AmeriFlux, AsiaFlux, CarboAfrica, CarboEurope-IP, ChinaFlux, Fluxnet-Canada, KoFlux, LBA, NECC, OzFlux, TCOS-Siberia, USCCC) and the Fluxnet project. M. Campioli, University of Antwerp, Belgium, kindly made available the data set he and his many colleagues compiled in 2015. I am grateful also to D Binkley, JJ Landsberg, M Mencuccini, J Merino, PEH Minchin, S Mori, K Ogawa, H Poorter and M Westoby, all of whom were very willing to respond to questions I had about various aspects of this work. I am grateful also to my colleagues P Saenger, RGB Smith and J Turner, all of whom made valuable comments on the manuscript.

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License ( http://creat iveco mmons.org/licen ses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.