浅谈压力式温度计示值误差测量结果的不确定度评定
2020-05-19谢鹏赓
谢鹏赓
(湖北清江水电开发有限责任公司,湖北 宜昌 443000)
目前我国对压力式的温度计进行测量时,其测量的依据为:《JJG310-2002压力式温度计检定规程》及《JJF1059-1999测量不确定度评定与表示》。首先,在测量过程中,测量人员要想保证结果的的可靠性,其测量期间所处的温度环境应该在15℃~35℃,测量空间的相对湿度不大于85%RH。其次,温度计上示值误差的测量应该基于二等标准水银温度计的示值为评定标准。最后,为了能够尽可能提高测量结果的准确,更好地评估结果的不确定性,测量人员还应当要最大限度的选择适合的测量方法,即测量人员将二等标准水银温度计(0~100℃)与被检压力式温度计(0~100℃、准确度为1.0级、分度值为 1℃)一同置于FLUKE恒温油槽中,采用比对法进行检定。
1 数学模型
压力式温度计示值误差数学模型为:
y=x-(t+d)
式中:y为被检温度计的示值误差;x为被检温度计在测量时的示值;t为二等标准水银温度计的示值;d为二等标准水银温度计的修正值。
2 灵敏系数
3 标准不确定度的评定
3.1 输入量x的标准不确定度u(x)
1)被检压力式温度计的示值重复性引入的标准不确定度u(x1):(采用A类标准不确定度进行评定)。
取0℃~100℃、精确度为1.0、最小分度值为1.0℃的两支压力式温度计,分别在40℃、50℃、60℃、80℃和100℃五个点进行10次重复性测量(均为正行程),得到10组数据,见表1,利用“贝塞尔”公式计算10组实验标准差s(xi)。
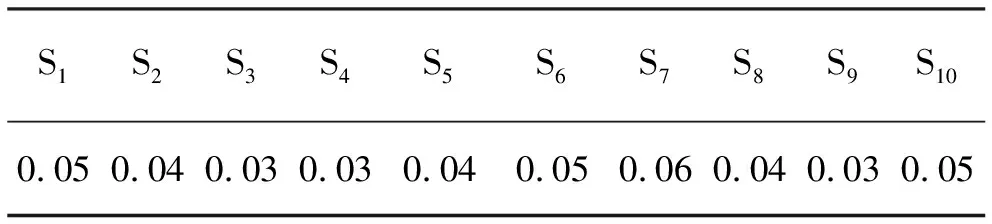
表1 10组测量数据表 ℃
所以:
u(x1)=0.043℃
自由度v(x1)=(n-1)m=90
2)被检压力式温度计的示值估读引入的标准不确定度u(x2):见表2(采用B类标准不确定度评定)。

表2 被检压力式温度计示值表
由于u(x1)、u(x2)不相关,所以:
自由度v(x)=140
3.2 输入量t的标准不确定度u(t)
1)二等标准水银温度计读数分辨率引入的标准不确定度u(t1):(采用B类标准不确定度评定)。

误差区间半宽a包含因子k标准不确定度u(t1)自由度v(t1)0.005℃3a/k=0.005/3=0.003℃(20%)-2/2=12
2)恒温油槽温场不均匀引入的标准不确定度u(t2):(采用B类标准不确定度评定)。

误差区间半宽a包含因子k标准不确定度u(t2)自由度v(t2)0.02℃3a/k=0.02/3=0.012℃(20%)-2/2=12
3)恒温油槽温度波动引入的标准不确定度u(t3):(采用B类标准不确定度评定)。

误差区间半宽a包含因子k标准不确定度u(t3)自由度v(t3)0.02℃3a/k=0.02/3=0.012℃(20%)-2/2=12
由于u(t1)、u(t2)、u(t3)不相关,所以:
自由度v(t)=24
3.3 输入量d的标准不确定度u(d)
1)二等标准水银温度计修正值引入的标准不确定度u(d1):(采用B类标准不确定度评定)。

误差区间半宽a包含因子k标准不确定度u(d1)自由度v(d1)0.06℃kp=2.58a/k=0.06/2.58=0.02℃∞
2)二等标准水银温度计在使用中不作零位修正引入的标准不确定度u(d2):(采用B类标准不确定度评定)。

误差区间半宽a包含因子k标准不确定度u(d2)自由度v(d2)0.06℃3a/k=0.06/3=0.035℃(20%)-2/2=12
输入量d标准不确定度为:
自由度v(d)=20
4 合成标准不确定度
表3中:i为不确定度来源序号;xi为第i个变量;ai为xi的区间半宽;ki为包含因子;u(xi)=α/k为B类标准不确定度;ci为灵敏系数;ui(y)=∣ci∣u(xi)为标准不确定度分量;vi为自由度。
以上所分析的各输入量的标准不确定度分量是互不相关,其合成标准不确定度为:
扩展标准不确定度为:
U=kuc(y)=2×0.07=0.14℃(k=2)
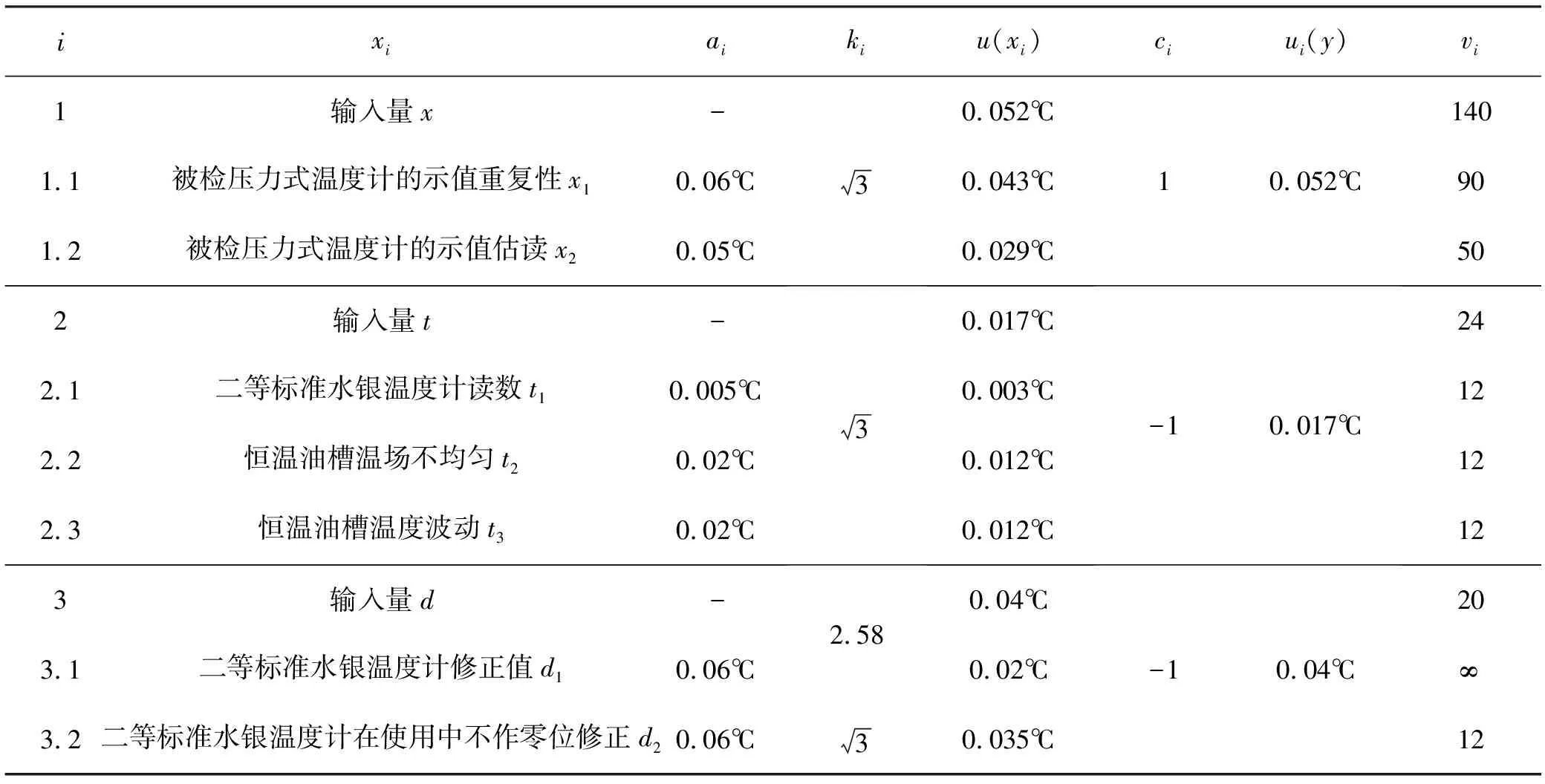
表3 合成标准不确定度表
5 测量结果的不确定度报告
检定环境温度:15℃-35℃;湿度:不大于85%RH;其示值误差测量结果的扩展不确定度:U=0.14℃,k=2。
6 结 语
综上所诉,被检压力式温度计示值误差测量结果的不确定度影响主要表现为被检温度计的示值重复性、恒温槽温度不均匀性和恒温槽温场波动。为了保证不确定度评定的可靠性,由此得到的扩展不确定度应满足:En=0.14℃/10℃≤1/3。
因此,采用上述方法用于检定压力式温度计示值误差是完全能满足相关的技术要求,其检定方法是可行的。为了保证压力式温度计测量结果不确定度评定具有较高的可靠性,在评估测量本身的不确定性时,试验人员需要对影响评定可靠性的各种因素进行全面的分析,找出温度计示值的误差,从而确保温度计能够更好地被投入使用。
