蒙特卡洛法在发动机推力测量不确定度评估中的应用

郑 科, 耿卫国,朱子环

(北京航天试验技术研究所，北京 100074)

0 引言

发动机常被用于卫星、火箭等的精确轨道控制和姿态调整，姿轨控发动机推力矢量直接关系到卫星能否入轨以及发射任务的成败；准确测出推力矢量参数，能够为发动机的在轨工作状态提供基本依据。目前推力矢量测量有多种方案，但在我国的发动机高空模拟热标定试验中，技术和工艺比较成熟且经多次飞行验证效果显著的，是北京航天试验技术研究所投入使用的转台推力矢量测量方法[1]和该所研制的基于压电的动态矢量推力测量方法[2-3]。

无论采用何种推力测量方法，推力矢量参数都不是直接测得，而是基于一定的数学模型通过计算间接得出，前期对推力矢量不确定度的评估，是依据国家计量技术规范《测量不确定度评定与表示》JJF 1059.1-2012中的GUM方法，对各个具体测得量进行评估后，按照不确定度传播率计算合成标准不确定度[4-5]。但针对多个输入量和单一输出量的测量模型，作为JJF 1059.1-2012的补充文件，国家计量技术规范《用蒙特卡洛法评定测量不确定度》JJF 1059.2-2012规范了一种评估测量不确定度的方法[6]，其核心内容是在建立测量模型的基础上利用对概率分布的随机抽样进行分布传播不确定度。本文基于压电式推力矢量架，在介绍其数学模型后，采用GUM法和蒙特卡洛法(MCM,Monte Carlo method)进行不确定度评估，对不确定度评估结果进行对比验证，比较两种方法的适用性。

1 压电式推力矢量测量

火箭发动机压电式推力矢量系统的数学测量模型如图1所示[7]。

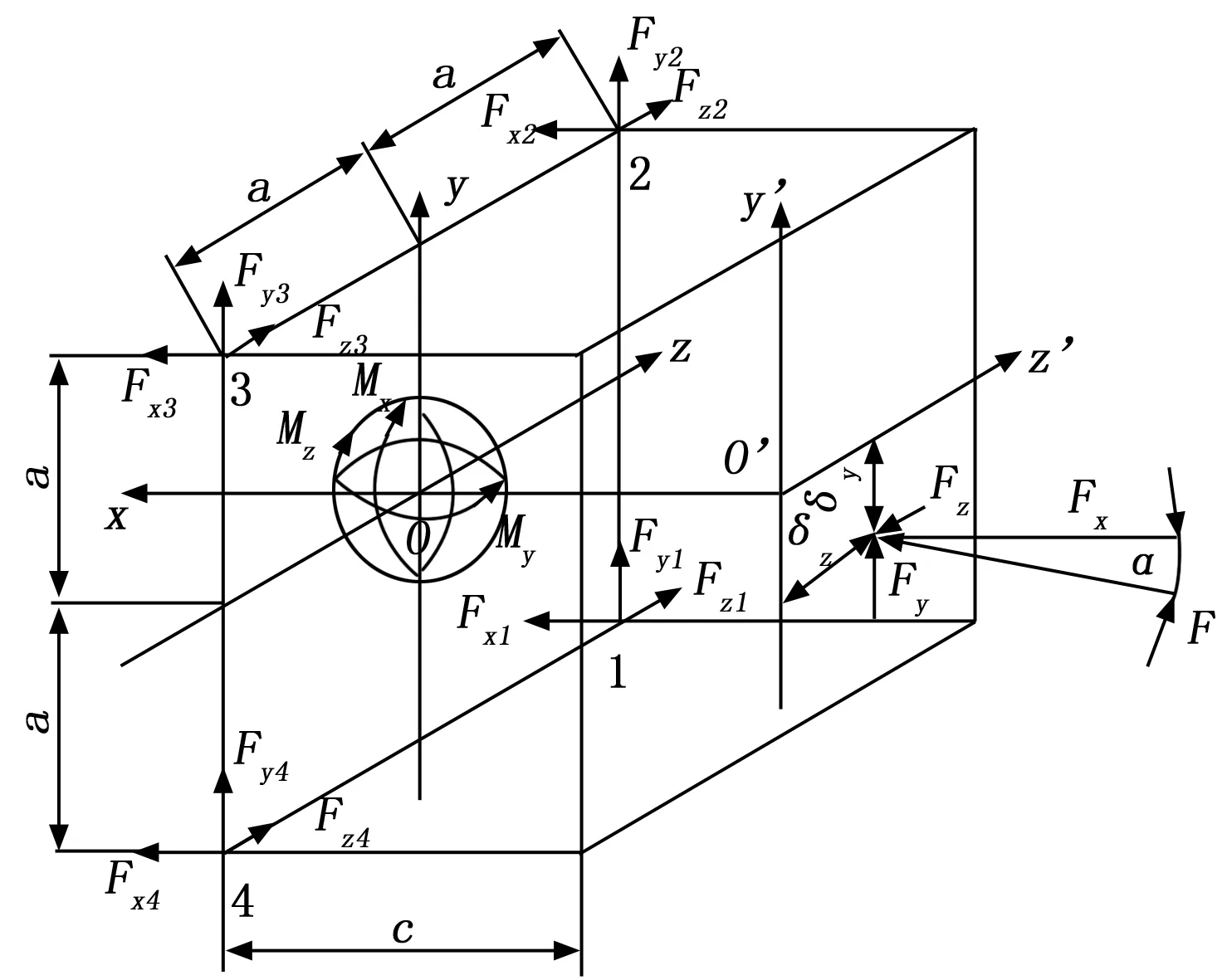
图1 某压电式推力矢量测量系统数学模型

图1中，O-XYZ为测力平台坐标系，O′-XY′Z′为火箭发动机坐标系。其中，YOZ为压电测力仪三维测力传感器的安装定位平面，O点为OX轴与三维测力传感器安装定位平面交点；Y′O′Z′为火箭发动机的安装定位法兰平面，O′点为火箭发动机喷管几何理论轴线与法兰平面交点。矢量力偏斜角为α，作用点为(δy,δz)。

F为姿轨控发动机点火产生的空间矢量推力；

Fx，Fy，Fz分别为矢量推力F在作用点(δy,δz)的三向分力；

Fx1，Fx2，Fx3，Fx4分别为通过测力平台上的4个排列成正方形分布的三维力传感器实际测得的X方向的4个分力。同样，Fy1，Fy2，Fy3，Fy4和Fz1，Fz2，Fz3，Fz4分别为通过传感器实际测得的Y方向和Z方向分力；

Mo为火箭发动机矢量推力F对测量平台坐标系中心产生的总力距；

Mx，My，Mz分别为总力矩Mo在各方向上的分力矩；

a为发动机测力平台上三维力传感器与坐标轴之间的距离；

c发动机测力平面上三维力传感器与法兰平面之间的垂直距离。

建立火箭发动机推力矢量参数的测量模型：

发动机的三项推力为:

(1)

推力矢量力矩为:

(2)

则得:

推力斜偏角α:

(3)

侧向力方位角:

(4)

推力偏移:

(5)

推力偏移方位角:

(6)

2 蒙特卡洛法不确定度评估

2.1 蒙特卡洛法原理

蒙特卡洛法计算测量不确定度是以概率统计为基础，利用随机抽样实现概率分布传递的一种数值计算方法，区别于GUM法的不确定度传播率，适用于可由任意多个概率密度函数(PDF,probability density function)表征的输入量和单一输出量的模型，尤其适用于各不确定度分量的大小不相近、输出量的估计值和其标准不确定度相当、测量模型明显呈非线性等典型情况[8-9]。

蒙特卡洛法为输出量的表征提供了一种方法，输出量Y的分布函数为。

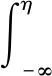
(7)

式中，GY(η)为输出量Y的概率密度函数。

gY(η)可由输入量Xi的概率密度函数gxi(ξi)通过测量模型传递得到，概率分布传递如图2所示，核心是对输入量的PDF重复采样，即利用对输入量概率分布的随机抽样代入数学模型进行分布传递，计算求得输出量Y的PDF的离散抽样值，因为离散抽样值GY(η)包括了输出量Y的数值特性，所以能够由输出量的离散分布数值求出Y的最佳估计值以及标准不确定度，Y的不确定度和包含区间等数值特性的可靠性可随着对输入量的概率密度函数的随机抽样数M增加而提高[10-11]。

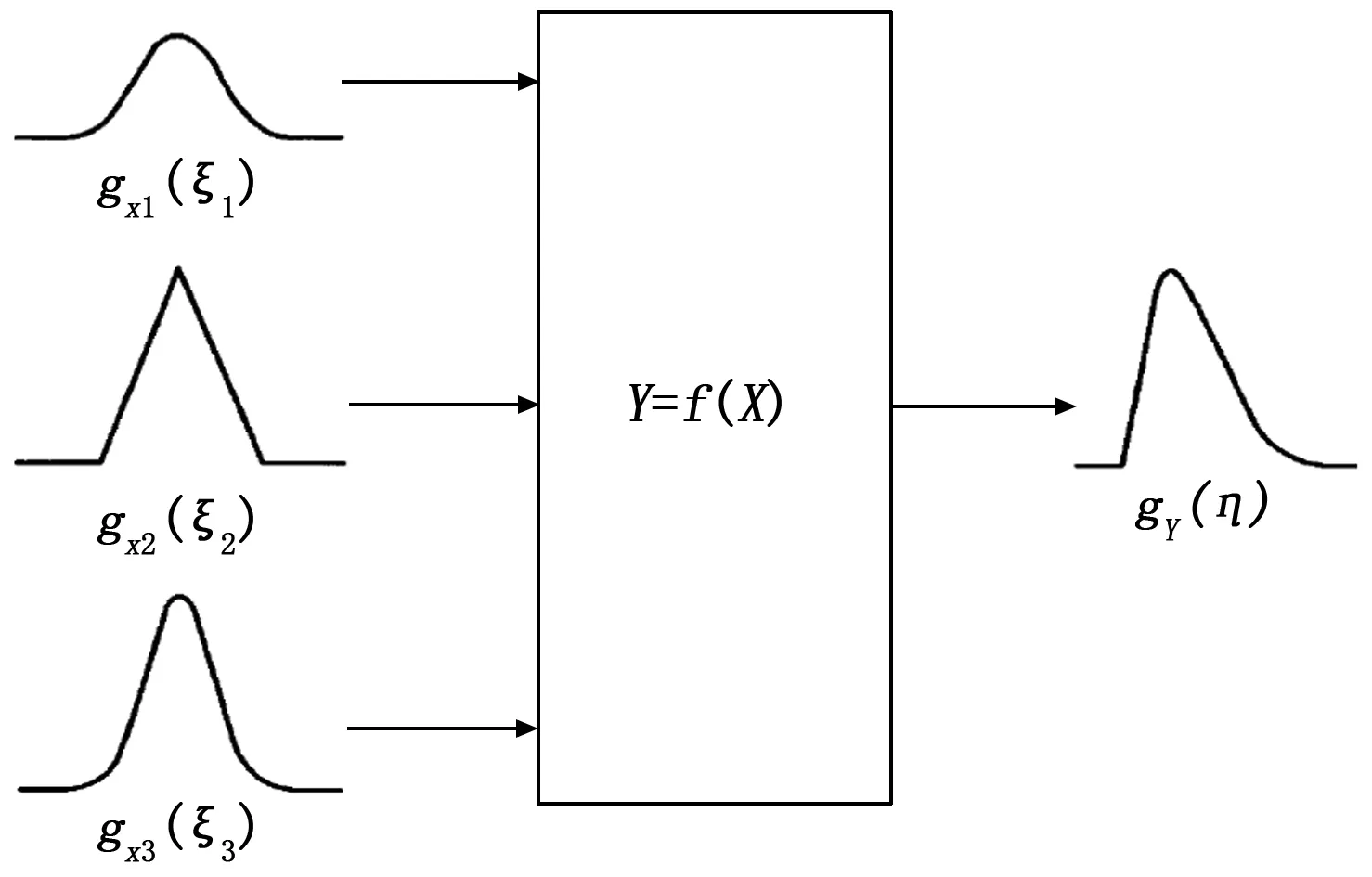
图2 由多输入量PDF得到单一输出量PDF的示意

MCM评估过程：

1)建立输出量Y和各个输入量X1,X2,…,Xn的模型Y=f(X1,X2,…,Xn)；

2)确定利用获得的先验信息，确定各输入量的概率密度函数gxi(ξi)；

3)确定MCM的仿真次数M；

4)从各个输入量Xi的概率密度函数中随机抽样M个样本值xir(i=1,2,…,N，r=1,2,…,M)；

5)对每个的样本矢量x1r,x2r,…,xNr)，代入模型得yr=f(x1r,x2r,x3r,…,xNr)(r=1,2,…,M)；

6)将计算得到的M个模型值按照递增顺序排序，得出输出量Y的离散表示G；

7)由输出量的离散表示G计算Y的期望值以及标准差，求出估计值y和不确定度μ(y)；

8)通过输出量的离散表示G求出给定包含概率下的包含区间[12]。

蒙特卡洛法的流程如图3所示。

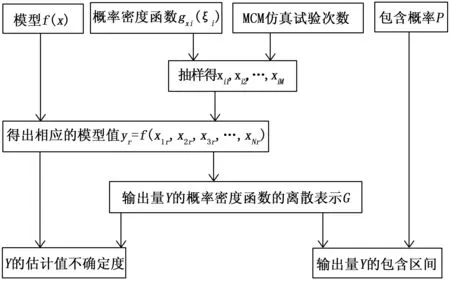
图3 蒙特卡洛法流程图

2.2 蒙特卡洛法的实现

2.2.1 概率密度函数的确定

针对输入量数据量小的问题，通常采用最大熵原理[13-14]求出各输入量的PDF，通过对每个输入量的概率密度函数进行M次抽样即解决了小样本数据量小的问题。

2.2.2 抽样仿真次数M

抽样模拟仿真次数M增加，样本容量的大小增加，蒙特卡洛法接近于输出量的真实总体。但如果M增多，随机抽样需要计算的时间越久，M减小，与输出量的实际情况偏离，计算不确定度的结果不准确。所以为了计算相对准确的不确定度需要合理的选择仿真次数M。

抽样仿真次数M的确定一般有两种方法：

1)一般情况下，M的值应至少大于1/(1-p)的104倍，包含概率p为0.95时，抽样仿真次数M:

(8)

2)一般要求测量结果的测量不确定度不超过两位有效数字时:

(9)

根据自由度的计算公式可得:

(10)

因此，抽样仿真次数M应该大于8×104，才能使评估结果的不确定度具有两位有效数字。

根据上述两种方法得到的计算结果，结合不确定度评估的实际经验，一般可以取抽样仿真次数M为106。

2.2.3 舍选法抽样

在使用蒙特卡洛法评估测量不确定度时，需要在各输入量PDF的约束下产生大量的随机数，对测量模型进行随机抽样，即产生随机变量，通过对产生的随机数进行模型传递以及统计计算，求得输出量的统计性质。

针对本文的小样本数据，在通过最大熵原理求出针对小样本数据的概率密度函数后，求得的概率密度函数分布不一定是常见分布，不能直接通过Matlab特定函数产生随机数，为了得到符合任意概率分布下的随机数，本文采用舍选抽样法[15-16]求随机数。

舍选抽样法的原理是：根据给定的输入量的概率密度函数f(x)，对概率分布为均匀分布的随机数序列{R}进行舍选。舍选的原则是当f(x)取值较大时，选择较多的随机数ri；在f(x)取值较小时，选择较少的随机数ri，从而使最后得到的子样本分布满足给定的概率密度函数。

输入量xi的概率密度函数为gxi(ξi)，在gxi(ξi)的约束下产生M个值xir(i=1,2,3,…,n,r=1,2,3,…,M)，若对n个输入量分别在其概率密度函数的约束下产生M个伪随机数，则可以得到M组向量:

(11)

2.2.4 蒙特卡洛法仿真结果

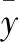
(12)

(13)

3 压电式推力矢量不确定度评估

3.1 测量数据

根据某次推力试车数据推导得出推力矢量参数如表1所示。

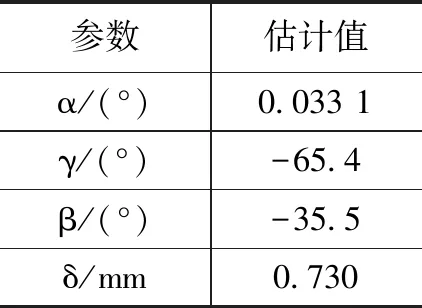
表1 某次试车推力矢量参数

表2～4为试车前X、Y、Z方向的推力检验值。

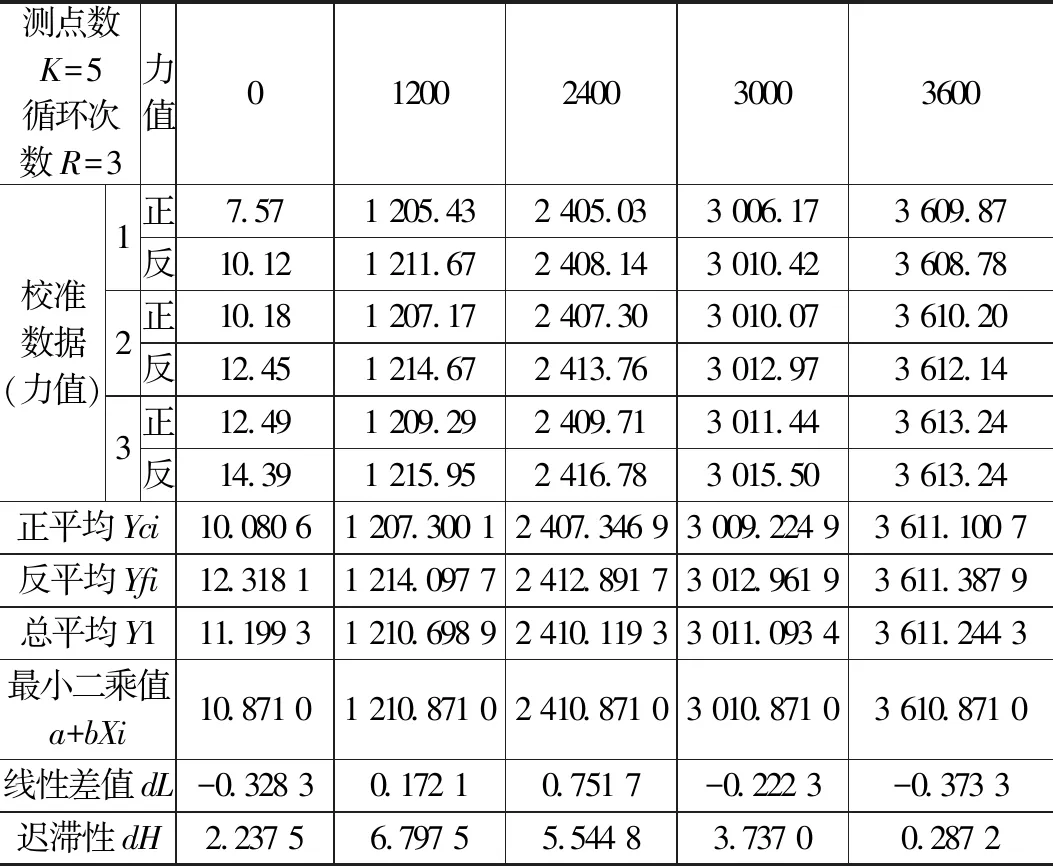
表2 压电式推力矢量系统X向静态标定

3.2 GUM法不确定的评估

计算参数合成不确定度一般表达式为:

(14)

式中,f为被测量y与直接测得量xi的函数关系。

由于Fx=Fx1+Fx2+Fx3+Fx4，是线性的，所以对Fx的A类不确定度计算如下：

根据合成标准不确定度推导：

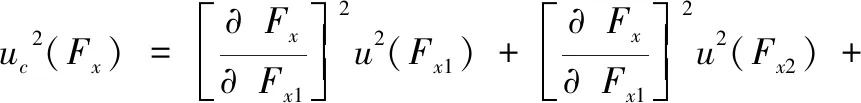
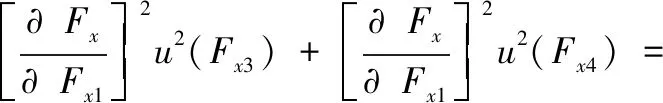
u2(Fx1) +u2(Fx2) +u2(Fx3) +u2(Fx4)

(15)

主推力合力的A类不确定度：

(16)

由前面章节推导公式得出推力矢量参数的合成不确定度。例如:

1)α的合成不确定度:

(17)

2)δ的合成不确定度:

(18)

通过上述表得出X、Y、Z方向的不确定度Ux，Uy，Uz，代入合成不确定度评估公式得出压电式推力矢量参数(α,γ,β,δ)的不确定度评估结果如表5所示。

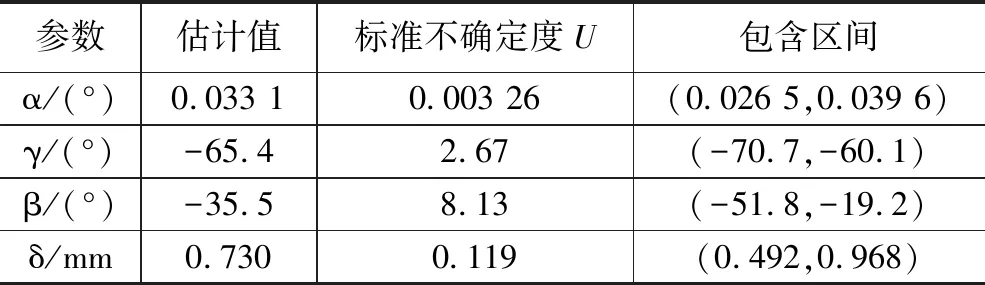
表5 GUM法推力矢量不确定度评估

表5中，扩展不确定度包含因子为k=2，包含区间的包含概率为95%。

3.2.1 GUM法的适用条件

在实际应用中，GUM法适用于以下条件：

1)输入量的概率分布可以近似是为对称分布；

2)输出量的概率分布可以近似是正态分布或t分布；

3)测量数学模型为线性模型或者能够用线性模型近似的模型[17]。

因此，GUM法具有一定的局限性。

当测量数学模型是复杂的非线性模型时，输入量的一阶偏导数通常不容易求解；根据泰勒级数展开，将非线性模型近似转化为线性模型，忽略了高阶级数项，带来了一定的误差，且每个输入量之间的相关系数难以计算；评估扩展不确定度时，一般取包含因子k为2或3，具有主观性，GUM法默认被测量的概率分布近似是正态分布或者t分布。

3.3 MCM的软件实现

图形用户界面(GUI，graphical user interfaces)是Matlab的一个主要功能，是根据用户体验和用户需求设计的可视化用户界面，一般由窗口、菜单、对话框等各种图形对象组成，用于与计算机、操作系统和应用程序互动交流，即使计算机产生某种动作，实现计算和绘图等功能[18-19]。

本文根据上文中的蒙特卡洛法流程利用GUI编写软件，固化流程，通过输入数据，进行直接计算，软件不仅可以计算推力矢量参数的不确定度，通过更改数学模型Y=f(X1,X2,…,Xn)，还可以计算发动机试验中温度、流量以及压力等的测量不确定度。

软件具体实施方式：

1)将发动机试验数据导入软件界面；

2)通过多组数据计算每个输入量的中心矩mi；

3)确定每个输入量的数据边界；

4)依据最大熵原理计算每组数据的概率密度函数gxi(ξi)，得出每个输入量的概率分布；

5)利用舍选抽样法进行抽样，随机抽样符合各个输入量Xi概率密度函数的M个样本值(xir(i=1,2,…，6，r=1,2,…，M)；

6)点击各输出量即参数测量模型，得出输出量的概率分布，从而给出不确定度及其给定包含概率下的包含区间。

将表3X方向的静态标定线性差值，以及表4Y方向、表5Z方向的静态标定线性差值导入不确定度评估软件中，如图4所示，不确定度评估结果如表6所示。

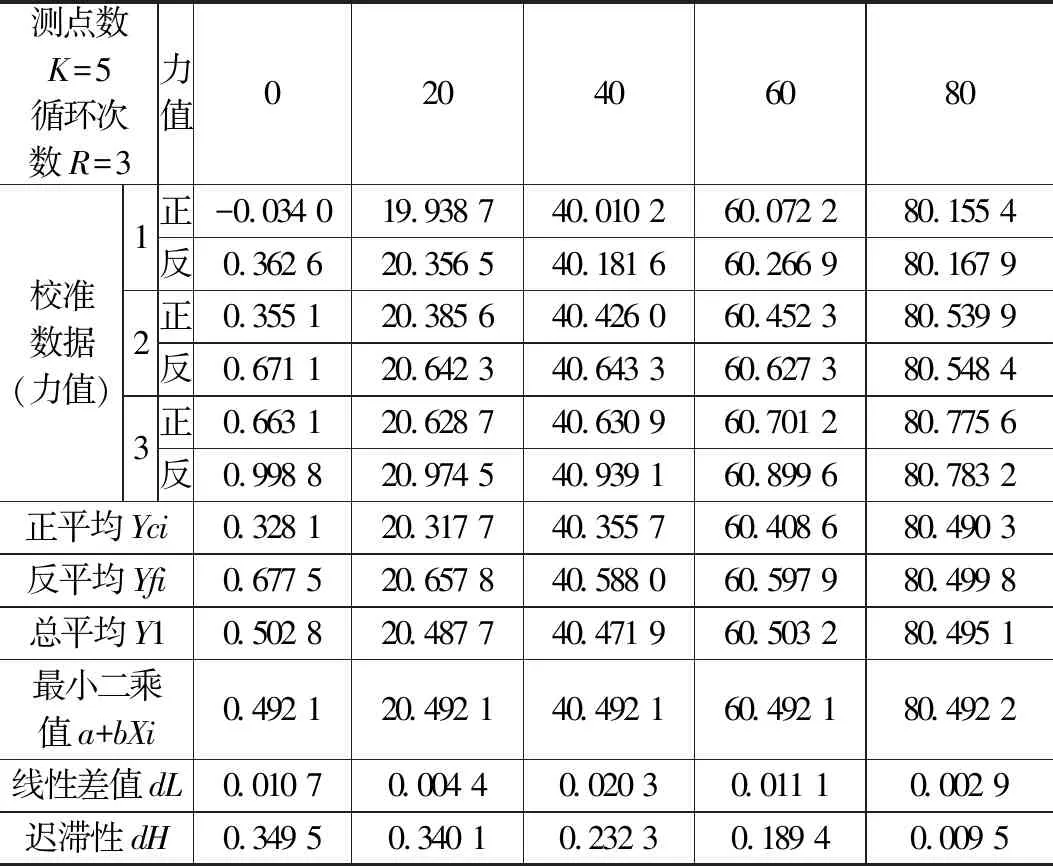
表3 压电式推力矢量系统Y向静态标定

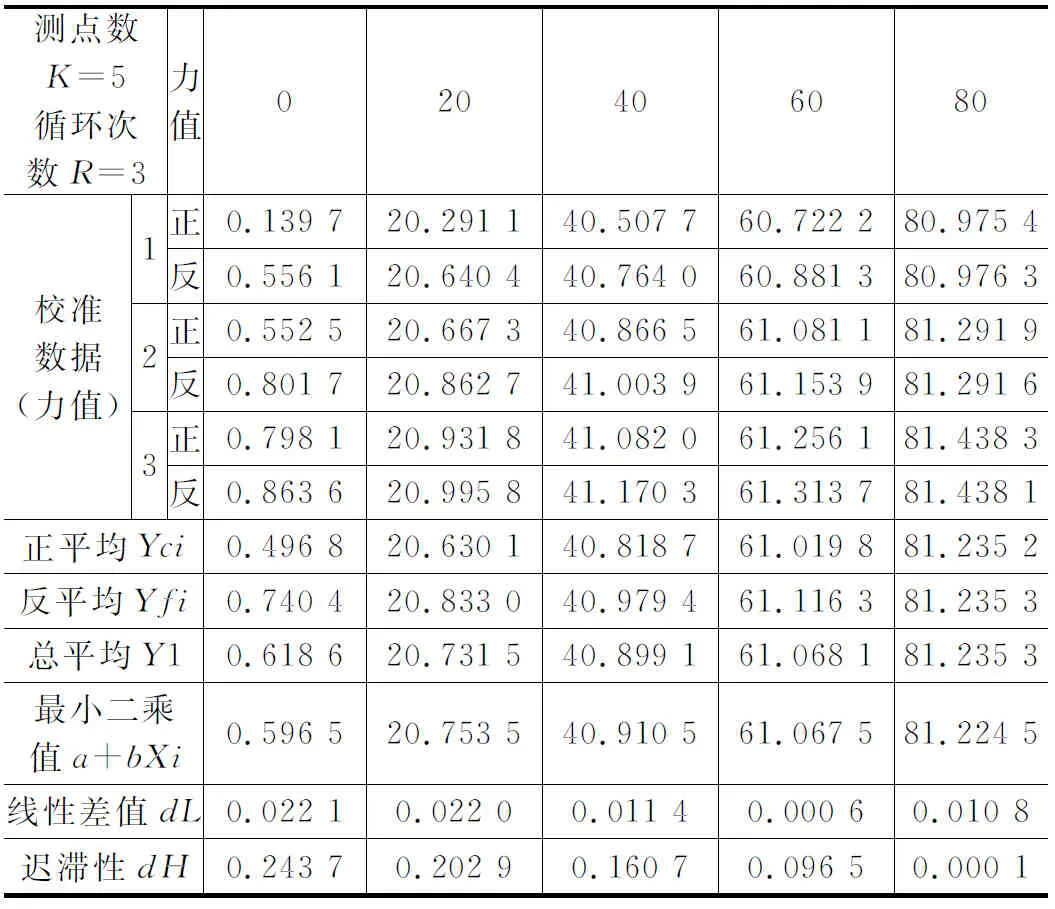
表4 压电式推力矢量系统Z向静态标定

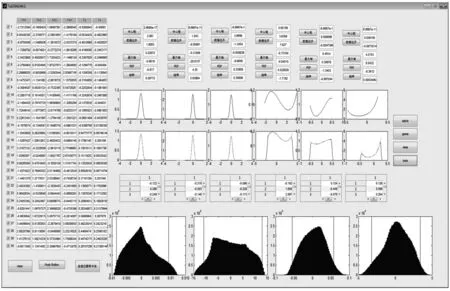
图4 MCM推力矢量不确定度评估

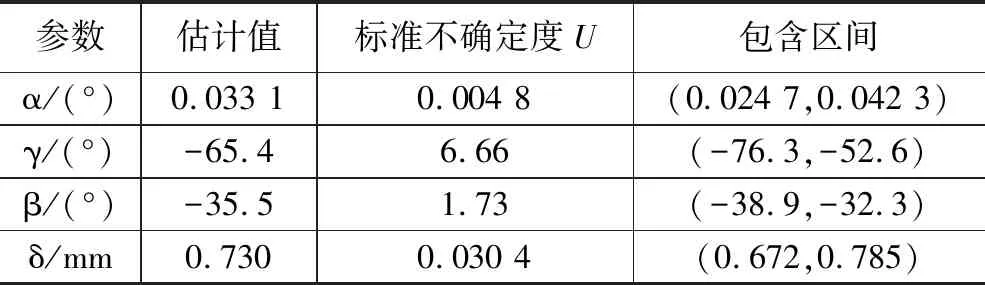
表6 基于MCM的推力矢量不确定度评估结果

表6中，给出的包含区间为包含概率为95%的包含区间。

图4中，导入输入量的小样本数据后，通过最大熵原理计算出输入量的概率密度函数，可以看出输入量的概率分布不一定为对称分布，利用舍选法抽样产生M个伪随机数，解决了输入量小样本的问题。

将在输入量概率密度函数的约束下产生的伪随机数代入测量模型，得到推力矢量参数的概率分布，输出量的概率分布不一定是正态分布或t分布，通过M个输出量的值求出不确定度以及给定包含概率下的包含区间。

3.3.1 MCM的适用条件

基于MCM的测量不确定度评估相比GUM法具有以下优点[20]：

1)对模型没有非线性的限制；

2)不受输入量的相关性和模型复杂性的影响；

3)不受输入量分布的影响；

4)不用假设被测量的分布；

5)不用计算偏导数和有效自由度。

3.4 GUM法与MCM的对比验证

MCM提供了验证GUM法的方法，当两者一致时，GUM法仍然作为测量不确定度的主要方法，当两者不一致时，应采用MCM。

验证方法：

1)应用GUM法得到输出量的概率p的包含区间y±Up；

2)通过运用自适应蒙特卡洛法获得输出量的标准不确定度u(y)以及概率对称或最短包含区间的端点值ylow和yhigh；

3)确定由GUM法及MCM获得的包含区间在约定的数值容差dt下是否一致，确定两个包含区间的各自端点的绝对偏差：

dlow=|y-Up-ylow|

(19)

dhigh=|y+Up-yhigh|

(20)

如果dlow≤dt，dhigh≤dt，则GUM法通过验证。

以α，δ为例：

1)推力斜偏角α。有效数字保留3位，数值容差dt=0.5×10-5，dlow=0.042 3-0.039 6=0.000 27>dt，dhigh=0.024 7-0.026 5=0.001 8>dt，GUM法没有通过MCM的验证。

2)推力偏移δ。有效数字保留3位，数值容差dt=0.5×10-3，dlow=0.968-0.785=0.183>dt，dhigh=0.672-0.492=0.18>dt，GUM法没有通过MCM的验证，相比MCM法较为保守。

4 结束语

对于压电式推力矢量不确定度评估，数学模型使用了复杂的非线性模型，输入量的概率分布不是对称分布，使用GUM法存在一定的局限性，MCM作为GUM法的补充，有更广的适用范围，依据各个输入量的概率密度函数进行随机抽样，计算得出M个结果，不仅解决了小样本测量数据少的问题，减少了大量人力物力的投入，还可以得出不用近似的包含区间，可以验证GUM法的有效性，可以作为发动机试验中不确定度评估的有效方法。