基于博弈组合赋权法的南欧江七级电站初期导流方案决策

贾鸿益，聂 鹏，岑黛蓉，陈 丽

(1. 昆明勘测设计研究院有限公司，云南 昆明 650051；2. 武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072； 3. 国家开放大学理工教学部，北京 100039)

在水利水电工程建设过程中，施工导流方案的选择关系到工程成本、导流规模、建设工期及系统风险等，科学且合理的导流方案决策是保证施工导流系统正常运行的前提。为保证施工导流系统的稳定性，国内外许多学者对施工导流方案的决策进行了深入的研究。胡志根[1]等建立导流系统综合风险分配机制，提出效用风险熵作为决策的综合评价指标。刘全[2]考虑梯级建设环境下导流风险受上下游电站影响，建立梯级电站施工导流风险测度模型，为施工导流标准决策提供了参考。

考虑到权重对决策结果影响较大，为探求权重与决策结果的关系，张衍[3]构建决策指标的三维空间映射，建立多目标决策的三维可视化模型，直观反映不同权重条件下导流方案的优劣性。指标权重主要分为主观权重和客观权重，分别反映各决策指标的主观倾向和客观属性。吴梦烟[4]引入距离函数将AHP法和熵值法计算得到的权重结果进行组合赋权，得到综合权重。毛红保[5]为进一步提高决策的精度，提出了一种基于区间估计的权重组合方法。任丽超[6]协调主观、客观权重既冲突又一致的关系，立足博弈论原理对风险指标的主、客观权重进行组合赋权。

得到不同方案中的各指标权重后，为对各方案进行决策分析，需要建立决策模型。徐曼[7]针对复杂决策系统的异构性问题,提出了基于Vague集的方案决策模型；张超[8]基于区间数理论建立区间数多属性决策模型，进行施工初期导流标准决策。张春生[9]针对工程特征引入趋同分组的方法，建立两层决策模型优选导流方案；孟卫军[10]综合考虑各候选方案相对于理想方案的接近程度，构建了多种指标类型共存的灰色关联TOPSIS决策模型。

基于博弈论的组合赋权法借鉴博弈论理论，将单一赋权方法看作是博弈中的局中人，以不同赋权方法的离差最小为博弈结果，对单一赋权方法进行赋权，并将其组合得到基于博弈论的组合赋权法[11]。本文基于专家调查法的主观赋权和基于熵权的客观赋权之间寻找一致，极小化主客观权重的偏差，得出各指标的组合权重，构建TOPSIS决策模型，选出最逼近理想解的方案。最后本文通过工程案例验证了该决策模型的准确性。

1 评价指标权重的确定

1.1 构建决策矩阵

在n个评价指标和m个方案的决策问题中，假设xij为第i个方案的第j个评价指标，构造评价指标特征矩阵X。为消除指标间由于量纲不同带来比较上的困难，根据评价指标的种类对指标特征矩阵X进行标准化，得到隶属度矩阵R：

其中：

1)效益型指标(越大越好)

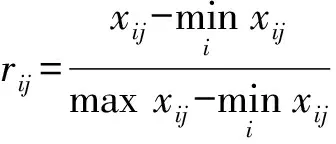
(1)

2)成本型指标(越小越好)

(2)

1.2 基于专家调查法的主观赋权方法

专家调查法又称德尔斐法，是以专家的知识和经验作为信息的来源，通过调查研究对问题做出判断、评估和预测的一种方法。适合在缺乏数据、多目标情况下确定指标权重[12]。

专家调查法的具体步骤为：确定需求指标，匿名征求专家意见，再进行归纳、统计，反馈结果是否发生偏差，若有偏差则重复上一轮，直至得到一致的意见。

1.3 基于熵权法的客观赋权方法

信息熵反映了信息的质量，是决策精度及可靠性的决定性因素之一。熵权法的核心是通过计算指标的变异程度来得出指标的信息熵，信息熵越大表示该指标的重要程度越低。信息熵能直观有效地反映各指标的差异程度[13-14]。使用隶属度矩阵R计算第i个评价指标的熵Hi和熵权wi。计算如下：

(3)

(4)

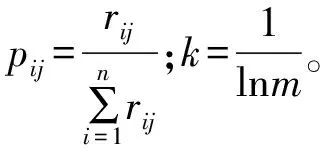
1.4 基于博弈论的组合赋权方法

主观赋权法能清晰的反应决策者意愿，但具有主观随意性，缺乏客观判断；客观赋权法建立在数值基础上，具有客观性，但受数据波动影响较大。而指标权重直接影响决策结果，故赋权方法不仅要反映主观意愿，还要反映客观事实。

1.4.1 主、客观权重博弈

进行方案决策时既要考虑决策者的主观决策，又要顾及客观事实，这是一个相互比较、相互协调的过程。博弈论是研究具有竞争性事物的理论和方法，是研究具有斗争或竞争性质现象的数学理论和方法，是分析多个决策主体行为相互影响时的理性行为及其决策均衡的工具。在博弈论中，当博弈多方出现多个决策方案时，可以假定每个方案都是理性决策的结果，即决策者为实现自身利益最大化或者自身损失最小化而进行的决策。在决策过程中，博弈各方协调一致去寻找最大化共同利益，竞争的结果不是由某一方决策者掌控的，而是由所有决策者共同实现的[15]。

在方案指标的确定过程中，主、客观权重作为博弈的局中人，在综合权重的确定过程中存在竞争，它们之间无法达成有约束力的协议，属于非合作博弈的范畴。因此，我们需使各个权重之间的偏差达到最小，即以纳什均衡为目标，在不同的权重之间寻找一致，进而得到综合权重。

1.4.2 基于博弈论的组合赋权法

借鉴博弈论理论，将基于专家调查法的主观权重和基于熵权法的客观权重看作是非合作博弈中的两个局中人，将两种权重达到的离差最小作为博弈结果，然后对专家调查法和熵权法所得的主、客观权重进行再次赋权，并将其组合得到基于博弈论的组合权重。基于博弈论的组合权重既不偏向于主观权重，也不偏向于客观权重，是权重之间进行非合作博弈，达到纳什均衡后的结果[16-18]。其组合赋权步骤如下：

1)计算主、客观权重后，构建权重向量的任意线性组合，即对主、客观权重进行再次赋权：

(5)

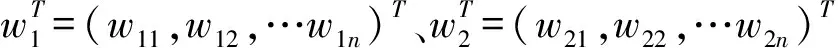
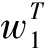
(6)

(7)

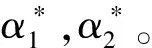
(8)

(9)

使用博弈论方法对主、客观权重进行组合赋权，能充分挖掘与利用主、客观权重的信息，保证组合权重与主、客观权重之间的偏差最小。弥补了现有组合赋权方法无法有效反映主、客观权重差异的不足，全面地考虑各指标之间的固有信息，减少主观随意性，提高了指标赋权的科学合理性。

2 基于组合赋权的TOPSIS决策模型

TOPSIS法也叫“逼近理想值法”，是一种距离综合评价法，通过构造一个各指标均为最优的理想方案，并在空间上计算各方案的指标与理想方案指标的欧式距离，反映各方案与理想解的贴近程度[9,14,19]，继而进行方案决策。

2.1 构建加权标准化矩阵

将隶属度矩阵R与组合权重w*相乘得到加权决策矩阵Y

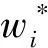
2.2 计算各方案的相对贴近度

相对贴近度Di为方案i与最优方案之间差距的数值化后的结果，其值越小，表明第i个方案越接近理想方案。相对贴近度的计算需进行标准化，Di介于0～1之间，当Di=0时，表明该方案就是理想方案，各指标均为最优；当Di=1时，表明该方案为最劣方案，各指标均为最差，根据相对贴近度的相对大小进行方案决策。计算过程如式(10) ～ (12)

(10)

(11)

(12)

在TOPSIS决策模型中权重占有十分重要的地位，本文借鉴博弈论的均衡思想，基于专家调查法得到各指标的主观权重和基于熵权法得到各指标客观权重，再运用基于博弈论的组合赋权法使主、客观权重作为局中人进行博弈，达到纳什均衡，并得到各指标的综合权重。最后在TOPSIS决策模型中计算各方案与最优解的相对贴近度，根据相对贴近度越小越优原则进行决策，得到最优方案。

3 南欧江七级水电站初期导流方案决策

3.1 工程概况

南欧江水电站位于老挝丰沙里省境内，坝址位于南欧江左岸支流南康河口下游约3.4 km，距其左岸支流Nam Khang 汇口下游约2.3 km，为南欧江梯级规划的第七个梯级。水电站工程枢纽建筑物主要由混凝土面板堆石坝、左岸溢洪道、左岸引水发电系统、右岸泄洪放空洞等组成，最大坝高约143.5 m。

该工程枢纽等级为一等大(1)型工程，拦河坝为1级建筑物。参考《水电工程施工组织设计规范》(DL/T5397-2007)的规定，导流建筑物级别确定为Ⅳ级，挡水标准为20～10年重现期洪水。考虑到南欧江七级水电站坝址处枯期流量与汛期流量相差较大，枯期流量仅为汛期流量的十分之一，故初期导流标准汛期按规范中相应挡水标准的高限选取，即上、下游土石围堰挡水标准为20年重现期洪水，相应设计流量为2 290 m3/s。

3.2 施工导流备选方案

结合南欧江水电站坝区地形地质条件、枢纽处自然条件、坝型及施工工期要求，且坝区枯水期水量小，洪枯比较大，且枯期时间较长，故在“全段围堰法拦断河床，隧洞泄流”的导流方式的基础上，根据围堰挡水时间提出了两个施工导流方案：全年围堰挡水的方案一及枯水期围堰挡水，汛期坝体挡水的方案二。各方案参数见表 1，施工导流备选方案的决策指标见表2。

表1 施工导流备选方案参数表

表2 施工导流备选方案的决策指标表

3.3 基于博弈论的组合权重计算

3.3.1 计算主客观权重

根据各导流方案的指标值构建指标特征矩阵X，由于确定性费用、不确定性费用、施工强度三个指标都属于成本型指标，故使用公式(2)进行标准化后得到隶属度矩阵R。

首先，使用专家调查法得到主观权重w1=(0.29,0.14,0.57)，然后使用熵权法确定各指标客观权重，使用公式(3)、(4)得到客观权重w2=(0.22,0.67,0.11)。

3.3.2 计算组合权重

为充分利用基于专家调查法得到的主观权重w1和基于熵权法得到的客观权重w2，保证组合权重同时估计主观决策和客观事实，使用公式(5)～(9)将主观权重w1，客观权重w2基于博弈论组合计算得到组合权重w*=(0.20,0.27,0.53)。

3.4 导流方案决策

将隶属度矩阵R与组合权重w*相乘构造加权决策矩阵Y。

使用公式(10)～(12)计算各方案的相对贴近度。方案的相对贴近度越小，与最优方案差异越小，即越小越优原则，进行方案决策。决策结果如表3。

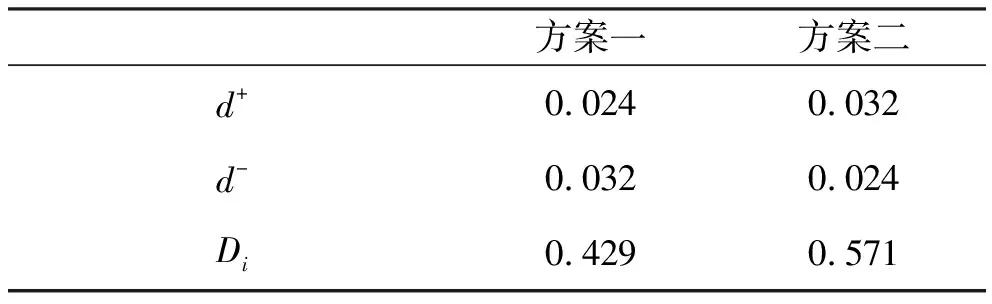
表3 相对贴近度表

在基于熵权法确定的客观权重中，不确定性费用权重(0.67)是确定性费用权重(0.22)的三倍，但一般认为在施工导流中确定性费用比不确定性费用更加重要，该客观权重不符合工程实际，说明根据仅各指标的熵权确定指标权重存在缺陷，客观权重的确定依赖于各方案指标的具体数值，易得出不符合主观认知的结果。如表4所示两个方案使用客观权重计算的相对贴近度分别是0.072和0.928，表明两个方案无可比性，显然这个结果是不合理的。基于专家调查法的主观权重分布较为合理，能普遍用于不同的工程方案决策，但缺少对于工程方案本身属性的判断，没考虑到工程的独特性。如表4所示，使用主观权重后方案一与方案二的相对贴近度分别为0.52和0.48，结果显示方案二要优于方案一，但方案一的确定性费用(6 310万元)与不确定性费用(5 144万元)均小于方案二的确定性费用(7 167万元)与不确定性费用(6 436万元)，仅方案一的施工强度(13.5×104m3/月)要稍大于方案二的施工强度(12.3×104m3/月)，最后却得出方案二要优于方案一的结论，说明主观权重也有其局限性。根据表3可知，方案一的相对贴进度(0.429)要小于方案二的相对贴近度(0.571)，那么可以认为方案一要优于方案二。因此推荐选用方案一，即围堰一次断流，隧洞导流方式，汛期围堰挡水，基坑全年施工方案。

表4 不同权重各方案的相对贴近度表

本文采用的基于博弈论的组合赋权法得出的组合权重能够在充分考虑决策者主观倾向的前提下，同时兼顾方案指标的客观属性，且组合权重为主、客观权重离差最小化后的结果，对主观权重还是客观权重都没有偏向性，是主、客权重进行非合作博弈后，达到纳什均衡后的结果。故使用基于博弈论的组合赋权法相比单独使用主、客观权重具有优越性。

4 结 语

施工导流是水利水电工程施工中的关键环节，其影响因素多，费用占比大，导流方案的选择存在困难。权重是方案决策的重要参数，故本文提出了一种基于博弈论的组合赋权法，将基于专家调查法的主观权重和基于熵权法的客观权重离差最小化后各自赋权，所得的组合权重能在清晰的反映决策者意愿的同时，兼顾指标数据的客观性，使主观倾向与客观属性较好地结合。并将组合权重代入TOPSIS决策模型中，建立决策矩阵，计算各方案与最优解的相对贴近度，继而对方案进行优选。南欧江七级水电站初级导流方案决策的实例，证明了该方法的可行性。