PDEs对四种图像降噪降维方法的影响

王 振 雷田田 范丽亚 杨 静

(聊城大学 数学科学学院,山东 聊城 252059)

0 引言

噪声图像的特征提取是模式识别和机器学习的重要组成部分,也是模式识别领域的研究热点之一.特征提取的本质就是降维,主要目标是利用线性或非线性变换,在保持原始图像蕴含的有效信息下,将处于高维空间中的图像压缩到一个低维子空间中,进而对图像做进一步识别.主成分分析(Principal Component Analysis,PCA)[1]和线性判别分析(Linear Discriminant Analysis,LDA)[2,3]是特征提取中两个最经典的方法.PCA的基本思想是通过极大化数据方差来寻找一组最优的低维子空间的正交基向量.LDA则是通过极大化Fisher准则来寻找降维变换阵,使得降维后的数据具有极大的类间散度和极小的类内散度,即降维后的同类数据尽可能靠近,不同类数据尽可能远离.PCA和LDA主要是针对图像的一组特征进行降维处理的,并不适用于多特征图像的维数约减.为了处理多特征图像的维数约减问题,H.Hotelling[4]于1936年提出了典型相关分析(Canonical Correlation Analysis,CCA).经典CCA主要是研究图像两组特征间的相关性,属无监督学习方法,为了引入监督信息,提高低维数据的鉴别能力,Sun等人[5]借助于类内信息提出了监督CCA(Supervised CCA,SCCA).杨等人[6]进一步提出了边界监督多重集典型相关分析.

不论是LDA还是SCCA都只是考虑了图像的判别信息,并没有考虑光照、遮挡、平移、旋转等对图像的影响,这限定了上述所提方法的推广能力.也有一些方法考虑了图像在平移、旋转和光照的影响,如SIFT (Scale-Invariant Feature Transform)[7]、HOG (Histogram of Oriented Gradient)[8]、Invariant Scattering Convolution Network[9]等,但没有考虑图像的判别信息.2013年和2015年,Liu等人分别提出了将PDEs应用于计算机视觉的方法[10,11].2017年,Fang等人[12]提出了一种基于PDEs的图像特征提取方法,所提方法既考虑了图像的判别信息,也考虑了图像在平移、旋转下的不变性以及对光照的鲁棒性,但没有考虑图像维数约减问题.2018年和2019年,江等人分别研究了PDEs的进化次数对图像特征质量的影响[13]以及对正则化SVM模型参数的影响[14].

本文借助于上述研究成果,着重考虑将PDEs融入到图像降维方法中,以期提高对高维噪声图像(光暗、有遮挡)的分类精度.为此,提出了基于PDEs的PCA (PCA/ PDEs)、基于PDEs的LDA (LDA/ PDEs)、基于PDEs的CCA (CCA/PDEs)以及基于PDEs的SCCA (SCCA/PDEs)四种图像降噪降维方法,并研究了PDEs的进化对四种所提算法的影响.为了验证所提算法的有效性和可竞争性,分别以支持向量机(Support Vector Machine,SVM,针对二分类问题)[15,16]和一对一多类SVM (One-versus- One Multi-class SVM,OVO-MSVM,针对多分类问题)[17,18]为分类器,在Extended Yale B数据集和Palm-print数据集上进行了大量的比较实验.

1 预备知识

本节简要回顾文中要用到的SVM和OVO-MSVM,以及一些基本概念.

1.1 二类支持向量机

线性SVM是通过构建下面的二次规划模型

(1)

来寻找分类决策函数f(x)=w,x+b,其中w∈Rd和b∈R分别是决策函数的法向量和阈值,C>0是模型参数,是松弛变量,‖·‖和·,·分别表示向量的欧氏范数和内积.通过求解模型(1)的Wolfe对偶模型

(2)

算法1(SVM)

步5 构造分类决策函数f(x)=w*,x+b*.

1.2 多类支持向量机

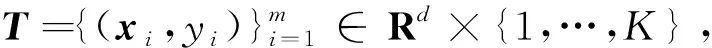
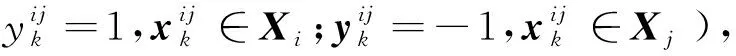
(3)

(4)

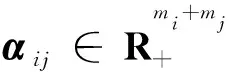
下面给出具体算法.

算法2(OVO-MSVM)

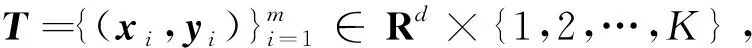
1.3 类间、类内及总体散阵

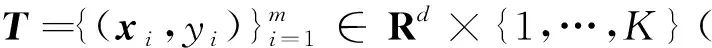
并称c和ci分别为总体均值和类均值.令

显然Sb,Sw,St均为对称非负定阵.称Sb,Sw,St分别为类间散阵(between-class scatter matrix)、类内散阵(within-class scatter matrix)和总体散阵(total scatter matrix).

2 基于PDEs的图像降噪方法

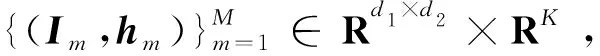
(5)

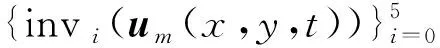
表1直至2阶的基本微分不变量

阶数i基本微分不变量invi(u)0,1,21,u,‖㔮u‖2=u2x+u2y3tr(Hu)=uxx+uyy4(㔮u)THu㔮u=u2xuxx+2uxuyuxy+u2yuyy5tr(H2u)=u2xx+2u2xy+u2yy

是直到二阶的基本微分不变量(见表1,其中u表示进化后的特征矩阵,u表示矩阵u的梯度,Hu表示u的Hessian阵,tr(Hu)表示矩阵Hu的迹,ux表示u对矩阵x求偏导),控制系数ai(t)与空间变量无关,其保证了图像的平移和旋转不变性.

为了求解模型(5),需先求解约束中的PDEs,为此离散化时间变量ti=i·Δt,i=0,1,…,N,并用前向差分离散时间偏导数,用中心差分离散空间偏导数,将PDEs转化为下面的迭代公式(具体推导见文献[11])

(6)

(7)

n=0,1,…,N-1,m=1,2,…,M,

(8)

其中η>0是搜索步长.

3 基于PDEs的四种降噪降维方法

对高维图像来说,如果不降维,可能会导致分类器学习时间过长甚至失效;如果维度降得过低,往往会导致分类精度的损失.为了在降噪降维的同时还能保持良好的分类精度,本节提出了基于PDEs的PCA(PCA PDEs)、基于PDEs的LDA(LDAPDEs)、基于PDEs的CCA(CCAPDEs)以及基于PDEs的SCCA(SCCAPDEs)四种图像降噪降维方法.

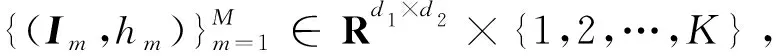
3.1 PCAPDEs

PCA/PDEs的基本思想是

首先,利用PDEs的进化对原始图像Im∈Rd1×d2进行降噪处理,得到特征矩阵um∈Rd1×d2.

最后,调整PDEs的进化次数,得最佳分类精度.

PCAPDEs的基本思想可直观地表述为

↑调整进化次数|

PCA的基本思想是在Rl中寻找一组标准正交基,使得降维后数据间的方差越大越好,即满足如下准则

(9)

其中c为样本均值.由于

所以模型(9)可等价地表示为

(10)

又因为对称非负定阵GTStG的迹等于其全部特征值之和,故可用矩阵的特征值分解求解模型(10),具体算法如下

算法3(PCAPDEs)

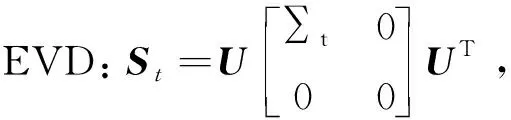
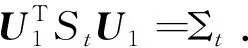
步5 若累计贡献率满足(λ1+…+λl)/(λ1+…+λt)≥85%(l≤t),取降维变换阵G*=U1∈Rd1d2×l.

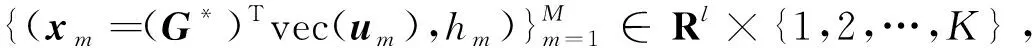
步7 选择分类器对低维向量集进行分类.

步8 调整PDEs的进化次数,得最佳分类精度.

3.2 LDAPDEs

LDAPDEs的基本思想类似于PCAPDEs的基本思想,只是在第2步中利用LDA进行降维处理.

不同于PCA考虑的是降维后数据间的方差越大越好,LDA考虑的是降维后的类内样本越凝聚越好,类间样本越分离越好,故满足下面的Fisher准则

(11)

所以准则(11)可表示为

(12)

可以分两种情况求解准则(12),一是Tr(GTSwG)=0的情况,另一是Tr(GTSwG)≠0的情况,本文只考虑第一种情况.下面给出具体算法.

算法4(LDAPDEs)

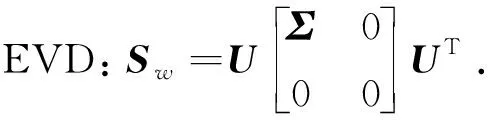
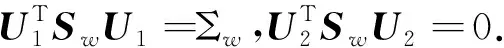
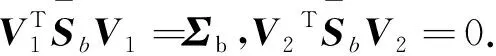
步8 取降维变换阵G*=U2V1∈Rd1d2×l.

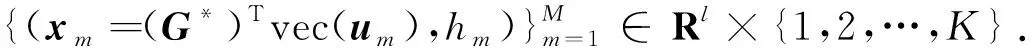
步10 选择分类器对低维向量集进行分类.

步11 调整PDEs的进化次数,得最佳分类精度.

3.3 CCAPDEs和SCCAPDEs

CCAPDEs和SCCAPDEs的基本思想是一样的,只是在降维环节采取的方法不一致.

首先,利用PDEs的进化对原始图像Im∈Rd1×d2进行降噪处理,得特征矩阵um∈Rd1×d2.

最后,调整PDEs的进化次数,得最佳分类精度.

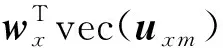
(13)

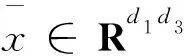
于是,模型(13)可表示为

(14)

其中

(15)

(16)

考虑模型(16)的Lagrange函数并令其关于决策变量的偏导数为0,可将模型(16)转化为广义特征方程

下面给出求解算法.

算法5(CCAPDEs)

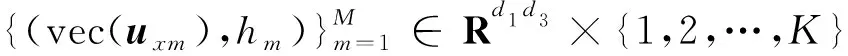
步3 利用(15)式计算矩阵Cxx,Cyy,Cxy.

步4 为了避免奇异性,置Cxx←Cxx+tId1d3,Cyy←Cyy+tId1(d2-d3),其中t>0是正则化参数.

步5 对Cxx做特征值分解(EVD):Cxx=UΣxUT,其中U∈Rd1d3×d1d3是正交矩阵,Σx=diag(σ1,σ2,…,σd1d3),σ1≥…≥σd1d3>0是Cxx的全部非零特征值.

步7 对矩阵B做奇异值分解(SVD):B=[P1ΣB,0]QT,其中P1∈Rd1d3×rB是列正交阵,ΣB=diag(λ1,λ2,…,λrB),λ1≥…≥λrB>0是B的全部非零奇异值.

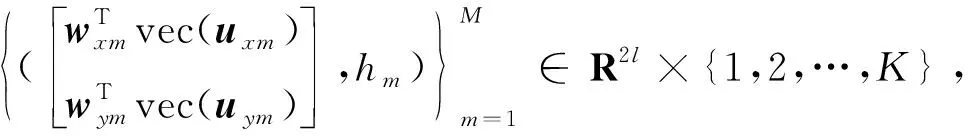
步10 调整PDEs的进化次数,得最佳分类精度.

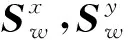
(17)

进而得到如下算法.

算法6(SCCAPDEs)

步1-2 同算法5中的步1-2.

步6-9 同算法5中的步7-10.

4 PDEs的进化对四种算法的影响

本节针对K(K≥2)类高维噪声(光暗、有遮挡)图像集,以分类精度为标准,通过实验研究PDEs的进化对四种算法的影响.对二类图像集,选用SVM作为分类器;对多类图像集(以三类图像集为例),选用OVO-MSVM作为分类器.分类器均采用五折交叉验证法.借助文献[13,14]的研究成果,PDEs的进化不超过10次.所有试验都在Extended Yale B人脸数据集和Palm-print掌纹数据集上进行,且分类器的模型参数通过网格搜索选择.为了直观验证PDEs的进化作用,选取了Extended Yale B人脸数据集中前5个人的第1张照片经过PDEs进化1-10后的图像(见图5).

4.1 数据集的选取

Extended Yale B人脸数据集包含38个人分别在12°,25°,50°,77°,90°的不同光照角度下的2414张面部图像,每张尺寸为48×42,向量化后的维度是2016维.随机选取10人(从左至右依次编号为1至10,见图1),每人前30张面部图像组成5个二类图像集以及随机选取15人(从左至右依次编号为1至15,见图2),每人前30张面部图像组成5个三类图像集进行实验

Palm-print掌纹数据集包含400个人的8000个掌纹,每人20个,前10个和后10个分别在不同时间获取,每个掌纹尺寸为n,向量化后的维度是1024维.随机选取10人(从左至右依次编号为1至10,见图3)组成5个二类掌纹集以及随机选取15人(从左至右依次编号为1至15,见图4)组成5个三类掌纹集进行实验

4.2 累计贡献率的选取

本节只考虑PDEs的进化对四种算法的影响,不考虑压缩函数的影响,故取g(x)=x.利用LDA降维后的数据维度只与数据类数有关,而利用PCA、CCA或SCCA降维后的数据维度均与累计贡献率的选择有关.累计贡献率的大小不仅决定着降维子空间的维度,而且还影响着图像的分类精度,一般常选为100%,但这样一来很多时候起不到降维的作用.本节以85%,90%,95%,100%四个累计贡献率为例,通过一系列实验发现,当累计贡献率为95%时,无论是对二类还是多类问题,降维后数据的分类精度都没有太大的损失,且在此贡献率下维度下降最快.为此,在下面的实验中累计贡献率均取为95%.

4.3 PDEs的进化对四种降噪降维算法的影响

在下面所有实验中(见表2至表17),每个表的第二列表示只是利用PCA、LDA、CCA或SCCA降维后的图像分类结果,第三至第十二列表示利用PCAPDEs、LDAPDEs、CCAPDEs或SCCAPDEs进行降噪降维后的分类结果,n表示PDEs的进化次数.

4.3.1 PDEs的进化对PCAPDEs的影响.表2和表3是10个二类图像集上的实验结果,表4和表5是10个三类图像集上的实验结果.对Extended Yale B中的10个图像集(5个二类,5个三类,下同),利用PCA可从2016维降到2-10维(不同的图像集略有不同,下同).对Palm-print中的10个图像集,利用PCA可从1024维降到2-15维.

表2 Extended Yale B中5个二类图像数据集上的实验结果(C=10)

表3 Palm-print中5个二类图像数据集上的实验结果(C=0.01)

表4 Extended Yale B中5个三类图像数据集上的实验结果(C=0.1)

表5 Palm-print中5个三类图像数据集上的实验结果(C=0.01)

从表2-表5中可以看出,利用PCAPDEs进行降噪降维,最多经过2次PDEs进化,其降噪降维后的分类精度明显高于只利用PCA降维后的分类精度.对Palm-print图像集,最多经过8次PDEs进化,精度可达100%;对Extended Yale B图像集,最多经过6次PDEs进化,精度可达93%以上(除一种情况外).

4.3.2 PDEs的进化对LDAPDEs的影响.表6和表7是在二类图像集上的实验结果,表8和表9是在三类图像集上的实验结果.不同于PCA、CCA和SCCA,LDA降维后的维度是类数-1,即对二类图像集,LDA降至1维,对三类图像集,LDA降至2维.

表6 Extended Yale B中5个二类图像数据集上的实验结果(C=1)

表7 Palm-print中5个二类图像数据集上的实验结果(C=0.01)

表8 Extended Yale B中5个三类图像数据集上的实验结果(C=0.1)

表9 Palm-print中5个三类图像数据集上的实验结果(C=0.01)

从表6-表9中可以看出,利用LDAPDEs进行降噪降维,最多经过5次PDEs进化,其降噪降维后的分类精度明显高于只利用LDA降维后的分类精度或保持不变.对Palm-print图像集,最多经过8次PDEs进化即可达到最佳精度,甚至达到100%;对Extended Yale B图像集,最多经过10次PDEs进化可达到最佳精度.

4.3.3 PDEs的进化对CCAPDEs的影响.表10和表11是在二类图像集上的实验结果,表12和表13是在三类图像集上的实验结果.对Extended Yale B图像集,利用CCA可从2016维降至72-80维;对Palm-print图像集,可从1024维降至4-24维.

表10 Extended Yale B中5个二类图像数据集上的实验结果(C=0.1)

表11 Palm-print中5个二类图像数据集上的实验结果(C=0.1)

表12 Extended Yale B中5个三类图像数据集上的实验结果(C=1)

表13 Palm-print中5个三类图像数据集上的实验结果(C=0.01)

从表10-表13中可以看出,除两种情况精度下降、两种情况精度保持不变外,利用CCAPDEs进行降噪降维,最多经过7次PDEs进化,其降噪降维后的分类精度明显高于只利用CCA降维后的分类精度,最多可提高66.67%的精度.

4.3.4 PDEs的进化对SCCAPDEs的影响.表14和表15是在二类图像集上的实验结果,表16和表17是在三类图像集上的实验结果.对Extended Yale B图像集,利用SCCA可从2016维降到46-80维;对Palm-print图像集,利用SCCA可从1024维降到2-4维.

表14 Extended Yale B中5个二类图像数据集上的实验结果(C=0.01)

表15 Palm-print中5个二类图像数据集上的实验结果(C=0.01)

表16 Extended Yale B中5个三类图像数据集上的实验结果(C=0.01)

表17 Palm-print中5个三类图像数据集上的实验结果(C=0.01)

从表14-表17中可以看出,利用SCCAPDEs进行降噪降维,对Palm-print图像集,最多经过3次PDEs进化,其分类精度可达100%;对Extended Yale B数据集,最多经过9次(大多数情况下最多经过7次)PDEs进化,其精度可达100%.明显好于只利用SCCA降维后的分类精度.

综上所述,本文提出的四种降噪降维算法明显好于PCA、LDA、CCA和SCCA四种降维方法,且通过PDEs的进化可以提高降维所带来的低分类精度.这对处理高维噪声数据的分类任务很有帮助.

5 结论

面对高维噪声图像(光暗、有遮挡)的分类任务,首先需要考虑的是对图像进行降噪、降维处理.现有的降噪方法大多不具备降维功能,同样地,现有的降维方法也大多不具备降噪功能.为了能够一体化进行降噪降维,且还能保持良好的分类精度,本文提出了PCAPDEs、LDAPDEs、CCAPDEs以及 SCCAPDEs四种降噪降维算法.通过在Extended Yale B人脸数据集和Palm-print掌纹数据集中选取的20个(二类和三类)数据集上进行的80组实验,可以看出所提的四种降噪降维算法明显好于PCA、LDA、CCA和SCCA四种降维方法,且通过不超过10次的PDEs进化可明显改善降维所带来的低分类精度.接下来将在本文的基础上进一步拓展PDEs的应用范围,并将其使用在更为复杂的应用场景中.