网格失配下MIMO-STAP稀疏字典构造方法

何 团，唐 波，张 进，张 玉

(国防科技大学电子对抗学院，安徽 合肥 230037)

0 引言

空时自适应处理(Space-Time Adaptive Processing, STAP)技术[1]是用于机载雷达系统在杂波背景下检测运动目标的关键技术。STAP技术的关键是获取待检测距离单元精确的杂波协方差矩阵。根据RMB(Reed-Mallett-Brennan)准则[2]，要使估计杂波协方差矩阵带来的杂波抑制性能损失小于3 dB，所需独立同分布训练样本数至少为2倍系统自由度。然而，实际环境中杂波分布往往是非均匀的，使得用于估计杂波协方差矩阵的训练样本数很难满足要求。近年来，稀疏恢复技术被应用到STAP中，只需少量训练样本即可实现杂波谱的精确恢复[3-4]。而多输入多输出(Multiple-Input Multiple-Output, MIMO)雷达STAP技术因其能够实现更好的性能[5-6]，稀疏恢复技术也慢慢扩展到了MIMO雷达中。

稀疏字典对稀疏恢复技术至关重要，但传统的稀疏字典还存在网格失配问题。当前，国内外众多学者针对网格失配问题，提出了很多有效的算法。文献[7]指出为减小网格失配影响，一种比较直接的方法就是增加网格的数量，但网格数过密集会使得计算复杂度显著增加，且会导致邻近导向矢量相关性过高，恢复精度急剧下降。文献[8]结合先验知识探索了正侧视和非正侧视条件下的多普勒网格间距调整问题，该方法通过杂波脊线的关系式能够对网格宽度进行自适应调整。文献[9]提出了一种参数寻优正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法用来估计网格失配，通过在局部范围内搜寻最优参数找到与真实导向矢量最匹配的原子。文献[10]提出了基于局部搜索OMP的网格失配STAP算法，该算法先从全局找到与真实导向矢量最匹配的原子，然后再从局部字典中搜索最优原子。

目前，针对网格失配问题提出的方法都是在网格失配的基础上，尽力减小网格失配的影响，都没能从字典源头上直接避免网格失配问题的产生。因此，本文直接从字典源头出发，针对MIMO-STAP稀疏方法求解杂波谱时存在的网格失配问题，提出了一种字典构造方法。

1 杂波谱稀疏恢复问题建模

1.1 MIMO雷达杂波信号模型

图1为机载MIMO雷达正侧视条件下的几何模型[11]，其中φ为杂波块的俯仰角，θ为杂波块的方位角，Φ为线阵方向与杂波块方向所成的空间锥角；V为载机速度，h为载机距离地面的高度。

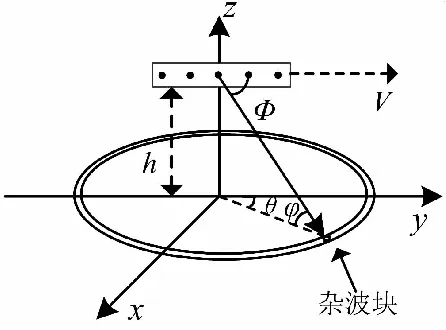
图1 机载MIMO雷达几何模型Fig.1 Geometric model of airborne MIMO radar

设均匀线阵体制下机载MIMO雷达天线发射的各波形满足正交关系,通过匹配滤波,可以在接收端分离出各个发射阵元信号。发射阵元个数为M，接收阵元个数为N。1个相干处理间隔(Coherent Processing Interval, CPI)内发射K个脉冲，脉冲重复频率为fr，工作波长为λ；发射阵元间距和接收阵元间距分别为dt和dr(一般为避免栅瓣问题，假定dr=λ/2)。

设φl为第l个距离环的俯仰角，将第l个距离环均匀切分为Nc个杂波块，θp为第p个杂波块的方位角。杂波块的空间频率为fs，多普勒频率为fd，则对应的空时导向矢量为：

v(fd,fs) =vd(fd)⊗vt(fs)⊗vr(fs)

(1)

式(1)中， ⊗表示Kronecker积，vt为发射导向矢量，vr为接收导向矢量，vd为时域导向矢量。发射和接收导向矢量分别为：

vt(fs)=[1 ej2πγfs… ej2π(M-1)γfs]T

(2)

vr(fs)=[1 ej2πfs… ej2π(N-1)fs]T

(3)

其中，γ为发射阵元间距与接收阵元间距之比；空间频率fs与θp、φl关系式为：

fs(θp,φl) =drcosθpcosφl/λ

(4)

时域导向矢量为：

vd(fd)=[1 ej2πfd… ej2π(K-1)fd]T

(5)

多普勒频率fd与θp、φl的关系式为：

fd(θp,φl)=2Vcos(θp)cosφl/(λfr)

(6)

正侧视条件下，杂波脊线各点的多普勒频率与空间频率之比为定值，该比值被称为折叠系数，可由以下式子求得：

(7)

式(7)中，V、dr、fr都可由先验知识精确得到，故折叠系数β可被精确估计。

则第l个距离单元的杂波信号可表示为：

(8)

式(8)中，σp为第p个杂波块的回波幅度，v(fd,p,fs,p)为第p个杂波块的空时导向矢量。

1.2 杂波协方差矩阵的求解

杂波分布在空时二维平面上具有稀疏性[4]，可由超完备字典近似表示为：

(9)

式(9)中，v(fd, i,fs, j)表示空时二维平面上空间频率为fs, j，多普勒频率为fd, i时所对应的空时导向矢量，σi,j为其幅度值；ψ为稀疏恢复使用的字典矩阵；σ为待求的稀疏参数矢量。

一般情况下，稀疏恢复的目的就是确定σ，则稀疏恢复问题最终可表示为：

(10)

式(10)中，y为不含目标信号的观测信号矢量，ε为噪声带来的误差阈值。

在求得稀疏参数矢量σ后，即可求得杂波空时功率谱为：

P=σ⊙σ*

(11)

在求得P后，杂波协方差矩阵可估计为：

(12)

2 克服网格失配的字典构造

2.1 传统字典缺点分析

如图2所示，一般情况下，为获得稀疏恢复所需的传统字典，需将整个空时二维平面网格化，将所有网格节点对应的空时导向矢量取出组成字典。设Q=NM，将fs和fd分别离散化为Ns格和Nd格，其中Ns=ρsQ，Nd=ρdK，ρs和ρd分别为fs和fd的离散化系数，超完备字典ψ的大小取决于ρs和ρd。目前ρs和ρd尚没有明确的最优值，只能结合具体问题给出经验化的取值。

图2 传统字典Fig.2 Traditional dictionary

对于MIMO-STAP，为了确保传统字典空间频率和多普勒频率取值范围将整个杂波脊线覆盖，字典的空间频率范围应满足：

(13)

式(13)中，fs max、fs min为空间频率可取的最大值和最小值。

字典的多普勒频率范围应满足：

(14)

式(14)中，fd max、fd min为多普勒频率可取的最大值和最小值。

空时二维平面横坐标为多普勒频率，其单位长度为：

Δfd=(fd max-fd min)/Nd

(15)

纵坐标为空间频率，其单位长度为：

Δfs=(fs max-fs min)/Ns

(16)

则传统字典的原子集合可表示为：

S={v(mΔfd,nΔfs)|m=0,±1,…,±Nd/2
n=0,±1,…,±Ns/2}

(17)

稀疏恢复技术在构建MIMO-STAP完备字典时，一般假定离散化后的网格节点与杂波脊线完全对准。然而实际情况下，网格节点与杂波脊线一般并不能完全对准，这就是网格失配问题。网格失配一般有两种情况：1)正侧视条件下杂波脊线的斜率不等于Δfs和Δfd之比；2)非正侧视条件下杂波脊线为椭圆曲线，椭圆杂波脊线与网格节点存在偏移。

因为非正侧视条件下网格失配问题很难有效解决，且一般机载雷达都在正侧视条件下进行目标探测，故本文只考虑解决正侧视条件下的网格失配问题。

如图3所示，在正侧视条件下，Δfs和Δfd的比值刚好等于杂波脊线斜率时，杂波脊线可以很好地定位在网格上，此时不存在网格失配，比如杂波脊线l1。当Δfs和Δfd的比值不等于杂波脊的斜率时，就会出现网格失配问题，比如杂波脊线l2。网格失配是目前传统字典存在的一个较大的问题。为了解决此问题，需要探寻新的字典构造方法。

图3 正侧视条件下网格失配示意图Fig.3 Schematic diagram of off-grid in side-looking case

2.2 网格失配字典构造方法

正侧视条件下，杂波脊线为一条直线，其斜率为：

k=1/β

(18)

折叠系数β可由先验知识精确得到，故斜率k也可精确得到。

如图4所示，沿杂波脊线方向及其垂直方向可形成多个网格，每个网格大小完全相同。设杂波脊线方向网格数为K1(K1为偶数)，杂波脊线垂直方向网格数为K2(K2为偶数)。一般来说，为保证恢复精度，K1取值相对要大，K2取值需要根据具体稀疏方法而定。如果稀疏算法只有在原子数较大的条件下才能获得较好的恢复性能，则K2取值不宜过小。反之，如果稀疏算法在原子数较小的情况下也能获得较好的恢复性能，则K2可取较小值，此时使用该字典在保证恢复精度的同时，还能极大地提升运算效率。因为考虑到本文字典需要对所有稀疏方法具有普适性，所以直接设定K1与K2相等。

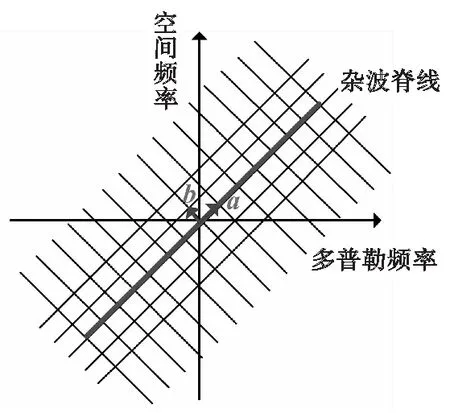
图4 网格失配字典构造Fig.4 Off-grid dictionary construction

对于单个网格，a，b为两基向量，基向量a与杂波脊线方向一致，基向量b与杂波脊线方向垂直。不同倍数的基向量相互组合可扩展成多个向量，所有向量的空时二维坐标值即可组成能克服网格失配的字典的空时二维坐标值。

基向量a，b分别为：

(19)

(20)

其中，d1，d2分别为a，b的模值，也就是单个网格的长、宽值。

设杂波脊线总长度为dmax，则

(21)

则基向量a的模值为：

d1=dmax/K1

(22)

基向量b的模值d2可根据实际杂波展宽程度确定，一般d2取值较小。尤其是非理想因素造成杂波展宽时，较小的d2可以提升杂波谱的恢复精度。

在确定两个基向量模值后，不同倍数的a，b进行组合可得到多个向量，具体表示为：

m·a+n·b

(23)

其中，

m=0，±1，…，±K1/2

(24)

n=0，±1，…，±K2/2

(25)

向量(m·a+n·b)对应的空间频率为：

(26)

多普勒频率为：

(27)

则字典原子的空时二维坐标为：

(28)

当m，n取遍所有值时，即可得到本文字典所有的空时二维坐标值。

还值得注意的是，本文字典空间频率和多普勒频率的范围肯定会大于传统字典。而过大的频率范围会对算法恢复性能产生影响，为了保证字典的性能，需要对字典进行削减。

如图5所示，直接将虚线框内的原子取出组成最终字典，即将空时二维坐标(fd,fs)同时满足以下式子的原子取出组成最终字典。

(29)

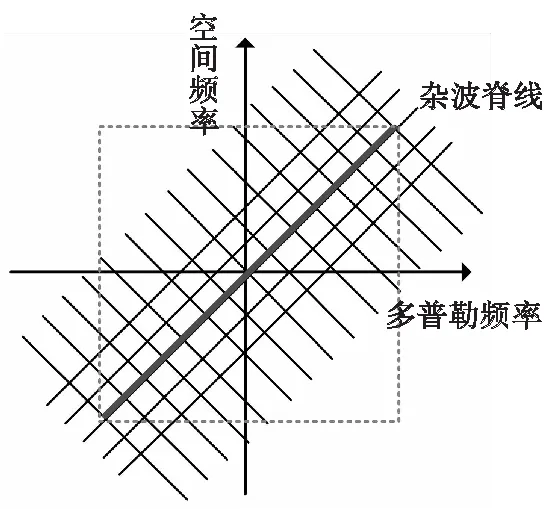
图5 削减字典Fig.5 Cut back on dictionary

通过对网格失配字典的削减即可使得其空间频率和多普勒频率取值范围不超过传统字典，从而保证稀疏恢复的精度。

构造克服网格失配字典的步骤可总结如下：

1) 根据机载先验信息，确定各种参数，由参数确定折叠系数β；

2) 确定基向量a，b两个方向的网格数K1，K2，并确定基向量a，b的模值d1，d2；

3) 找到所有网格节点，确定所有网格节点的空时坐标值，根据这些空时坐标值获得空时导向矢量，将所有空时导向矢量取出。

4) 削减所得空时导向矢量集合的范围，从而得到可有效解决网格失配的字典。

3 仿真分析

均匀线阵体制下的机载MIMO雷达仿真参数如表1所示。

表1 仿真参数

本节将对传统字典和本文字典在网格失配条件下的性能进行比较。传统字典ρs取2，ρd取4，即Ns取32，Nd取32。为了比较的公平性，本文字典K1、K2都取32，d2与d1取相同值。

3.1 字典网格节点分布图

为直观认识传统字典和本文字典的原子分布，本小节将β取0.7时两种字典的网格节点分布图进行展示。由图6可以看出，当β取0.7时，杂波脊线不能很好地定位在传统字典网格节点上，网格失配问题十分明显。而杂波脊线却能很好地定位在本文字典网格节点上，不存在网格失配问题。

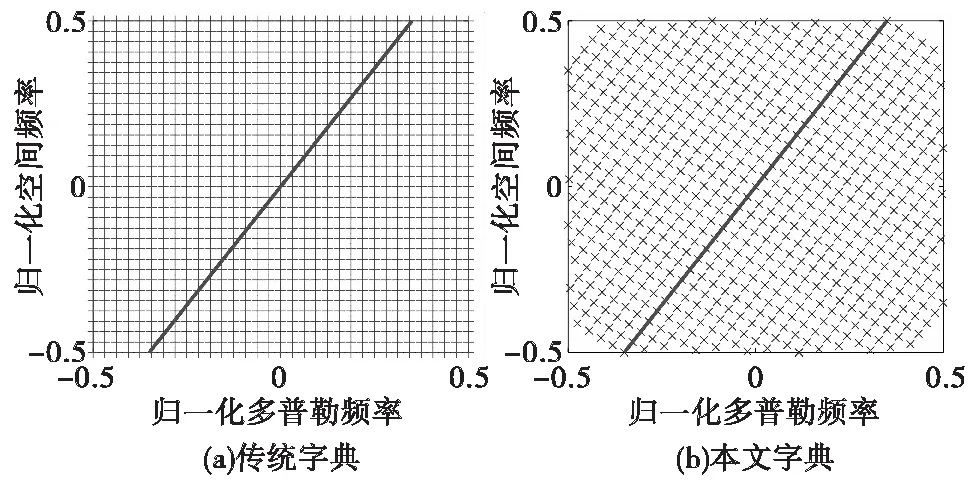
图6 字典网格节点分布图Fig.6 The distribution diagram of dictionary grid node

3.2 输出SINR比较

为比较传统字典和本文字典对各稀疏算法杂波谱恢复精度的影响，采用输出信干噪比(Signal-to-Interference-plus-Noise-Ratio, SINR)作为衡量基准。SINR(无有源干扰时)定义为输出信号与输出杂波加噪声信号能量的比值，具体表示为：

(30)

式(30)中，vt为目标信号矢量，R为杂波协方差矩阵与噪声协方差矩阵之和。

考虑三种场景来模拟现实环境:1)理想情况下，每个训练样本的杂波信号独立生成，杂波块的复振幅为满足复高斯分布的独立随机变量；2)存在时域非理想因素，主要考虑杂波内部起伏，采用Ward提出的杂波内部起伏模型[8]。模型的时间自相关函数服从以下分布:

(31)

式(31)中，T为脉冲重复周期，σv为速度标准偏移量，设置为0.2。3)存在空域非理想因素，主要考虑角度独立的阵列误差。假设阵列误差的幅度和相位均为窄带模型[8]，且幅度误差和相位误差分别服从以下均匀分布:

(32)

(33)

设置Δea为0.01，Δep为1°。

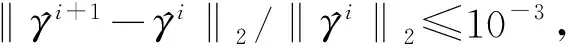
图7中每张图都包括SBL和LIKES两种算法分别使用传统字典和本文字典的输出SINR曲线。在理想条件下SBL、LIKES算法使用本文字典的输出SINR性能要远优于传统字典。在杂波内部起伏和阵列误差条件下，SBL、LIKES算法使用本文字典的输出SINR性能依旧要优于传统字典。因此，不论是在哪种条件下，存在网格失配时，SBL、LIKES算法使用本文字典的输出SINR性能都要优于传统字典。

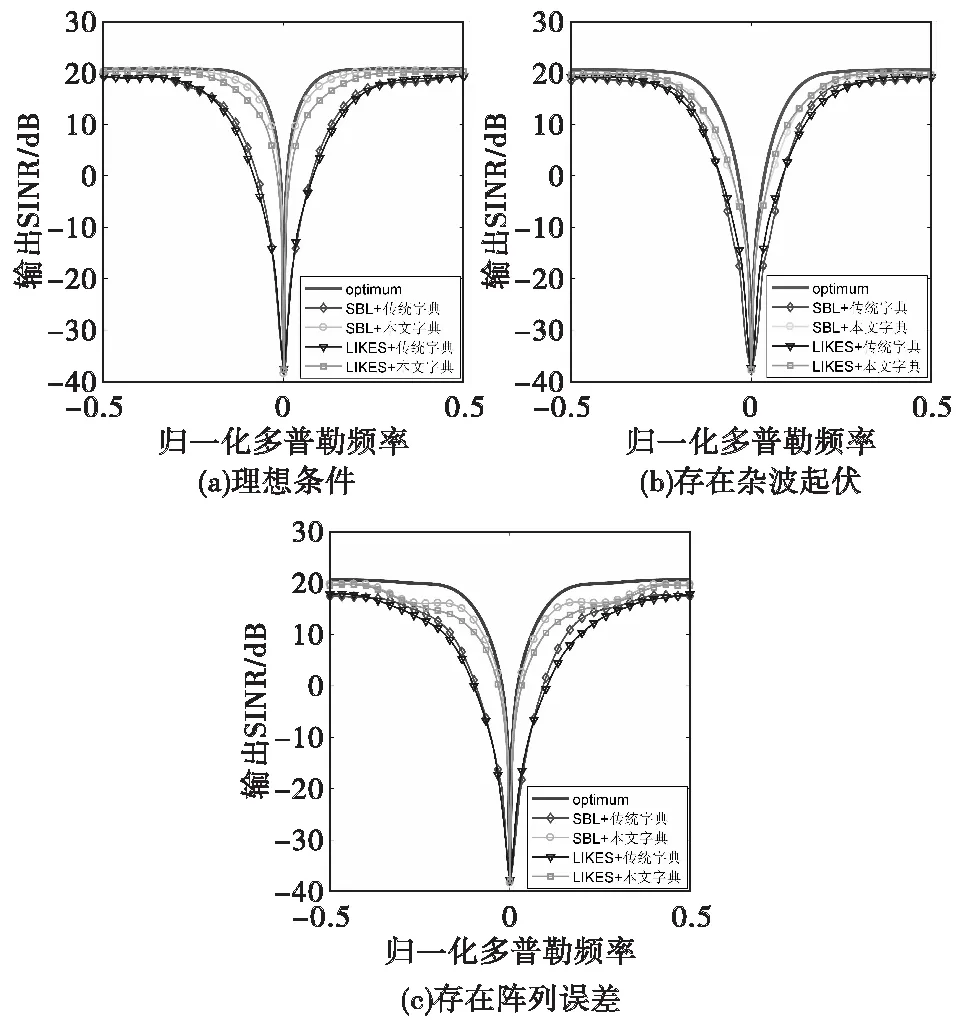
图7 不同条件下输出SINR比较Fig.7 Comparison of the output SINR under different conditions

4 结论

本文提出了一种网格失配条件下MIMO-STAP稀疏字典构造方法。该方法利用先验知识确定正侧视条件下的杂波脊线，然后沿杂波脊线方向及其垂直方向形成网格，将网格节点对应空时导向矢量取出组成并将空间频率和多普勒频率超出最大取值范围的原子去除以得到最终的字典。仿真实验表明，本文字典能够有效克服网格失配问题，网格失配条件下稀疏算法使用本文字典的输出SINR性能要远优于传统字典。