江泽涵译著《拓扑学》探析*

曾 汇

(1.中国科学院 自然科学史研究所,北京 100190;2.中国科学院大学,北京 100049)

拓扑学是一门相对分析学、代数学发展较晚的现代数学分支学科.这一学科自20世纪30年代传入中国,清华大学、北京大学、“中央大学”等高校数学系相继开设拓扑学课程.[1]江泽涵是中国传播拓扑学的先驱与发展拓扑学的奠基人.全面抗战时期,他着手翻译德国数学家沙爱福(H.Seifert,1907-1996)和施雷发(W.Threlfall,1888-1949)合著的《拓扑学教科书》(Lehrbuch Der Topologie),于1947 年出版了译著《拓扑学》.[2]这本译著是中国首部中文拓扑学教科书.他的出版改变了中国一直没有中文拓扑学教科书的状况,促进了拓扑学在中国的传播和发展.

关于江泽涵的这部译著,学界先前关注较少.目前,仅有陈克胜在其以博士学位论文为基础撰写的专著《民国时期中国拓扑学史稿》[3]中概括了这部译著的各章节内容,并述及相关的本土化问题,但未结合相关背景,充分利用其底本对这部译著进行系统研究.文章主要依据原始文献,围绕江泽涵这部译著的原作者与底本、翻译背景、翻译情况以及社会影响等问题进行探讨,以就教于方家.

1 《拓扑学》的原作者与底本

江泽涵所译《拓扑学》的原作者之一——沙爱福,1907年出生于德国一个名为贝恩施塔特(Bernstadt)的小镇.1926年,他考入德累斯顿工业大学(Dresden University of Technology).[4]沙爱福于1927年开始学习拓扑学,由施雷发教授授课.这是沙爱福第一次接触拓扑学,他便对此产生了极大的兴趣.1928 年,他赴格丁根大学(University of Göttingen)学习.当时,这所大学是世界一流的数学中心,有拓扑学家霍普夫(Heinz Hopf,1894-1971)任教.沙爱福于1930年获理学博士学位,1932 年又获哲学博士学位.此后,他一直致力于代数拓扑学的研究和教学.1935年,他成为海德堡大学(University of Heidelberg)教授,在该校教授拓扑学至1975年.[4]

《拓扑学》的另一位原作者——施雷发,于1888年出生在德国德累斯顿(Dresden),他的父亲是剑桥大学的一名植物学家.1907年,他从德累斯顿的一所名叫皇家人文的中学(Humanistischen Königlichen)毕业,并考入耶拿大学(University of Jena).他在大学主修化学,但也学习数学课程.1911 年,施雷发进入格丁根大学正式学习数学.1921 年他又进入莱比锡大学(University of Leipzig)学习数学,并于1926年获得博士学位.[5]毕业后,施雷发于1927年开始在德累斯顿工业大学教授拓扑学.他教学时没有正式教材,授课使用的是自己编写的讲义.沙爱福是他那时的学生之一,他们之间不仅是师生,更是研究伙伴.1934 年出版的《拓扑学教科书》(Lehrbuch Der Topologie)是他们两人共同研究成果的一部分.1938年,施雷发成为法兰克福大学(University of Frankfurt)的一名正式教授.[4]

1934年,沙爱福和施雷发合著的《拓扑学教科书》[6]出版.该书共十二章,第一章介绍了拓扑学的某些概念,包括同痕、同伦、同调和高维流形.第二章定义了几何基础,如领域空间、变换、点集、叠合等.这两章分别是直觉的讨论和单纯的复合形,主要对研究内容做简单引入,建立一种拓扑学的氛围.

第三章至第五章主要讨论基本拓扑概念以及性质,如链、边缘、同调群、广义上的单纯形、广义同调群以及维数、复合形、边缘的不变性.其中,第三章介绍了计算同调群的方法以及复合形的分类和性质;第四章通过证明逼近定理进而证明单纯同调群的拓扑不变性;第五章在前一章的基础上,通过将一点看作局部,将“全局的”不变性引申为“局部的”不变性,证明时使用了局部同调群来建立复形的维数和其他性质的不变性.

第六章至第八章介绍了曲面拓扑学、基本群、复叠复合形的相关概念,以及如何计算棱复合形和闭曲面的基本群,通过多边形叠合成多面形来解决高维空间的方法,引入基本群来解决高维复合形和流形的同胚问题以及复合复叠性的相关性质.

第九章和第十章分别介绍了三维流形和n维流形,主要从几何角度去讨论流形的性质.第九章介绍了构造和分析三维流形方法及其定向性的判定,在小节中也阐述了三维流形的普遍性质和求三维流形的示性数和基本群的方法.第十章将流形的讨论推广到n维情况,由于有第九章的内容为其做基础,因此相关的性质可以做推广.

第十一章是连续变换,讨论了前面涉及的复合形和流形之间的许多变换以及相关概念和性质.最后一章是群论中的定理,主要介绍群论知识,如同构变换、商群、Abel群.这些概念是近世代数学的基本定义,可将其作为备用知识.

《拓扑学教科书》与美国数学家韦布伦(Oswald Veblen,1880-1960)先前出版的《位置几何学》(Analysis situs)、俄裔美籍数学家莱夫谢茨(Solomon Lefschetz,1884-1972)的《拓扑学》(Topology)等著作不同,他以一种较清晰的方式来阐释书中的定理,出版后反响很好.当时有评论称“沙爱福和施雷发这本书开创了拓扑学的新纪元”.①英文原文为“The book of Seifert and Threlfall marked a new era in this history”.[7]而希尔斯(Tucker,A.W.,1905-1995)将《拓扑学教科书》与《与恩斯特·斯坦尼茨在拓扑学的要素下一起讲述多面体理论》(with Ernst Steinitz Vorlesungenüber die Theorie der Polyeder-unter Einschluss der Elemente der Topologie)做比较,认为前者最鲜明的特点是教科书,他讲述了现代拓扑学的基础.其写作目的是让学生了解当今拓扑学的深远发展,进而了解其根本思想.[8]《拓扑学教科书》于1934 年初版后,相继于1947年和1968年在纽约两次印刷,1980年在纽约再版,后于2000年和2006年相继印刷,对德国拓扑学的发展产生重要影响.

2 《拓扑学》的翻译背景及原因

现代数学源于西方,微积分、笛卡尔坐标系的出现开启了新的研究领域.19-20世纪数学各分支在西方持续发展,而后也有新的数学分支出现,如19世纪末出现的罗素悖论,后来发展为数理逻辑.与此同时,拓扑学这个新兴学科方兴未艾,他源于18世纪,以欧拉(L.Euler,1707-1783)发表论文解决“哥尼斯堡七桥问题”为标志.[9]德国著名数学家麦比乌斯(A.F.Möbius,1790-1868)在19世纪提出“四色问题”,1858年他发现了“单侧曲面”,也就是“麦比乌斯带”.1895年,法国数学家庞加莱(H.Poincaré,1854-1912)发表《位置分析》(Analysis situs)一文,之后他相继发表了4篇补充论文,这5篇论文基本构成了组合拓扑学的框架,[9]标志着拓扑学学科的正式诞生.进入20世纪后,相继有数学家发表相关论文,拓扑学开始进入蓬勃发展的时代.直至1935年,拓扑学已有新的突破,开始发展成一门相对成熟的学科.

相比西方,现代数学在中国起步较晚,在第一次鸦片战争后才有规模地从西方引介.清政府在甲午海战战败后,加快了学习西方和发展现代教育的步伐,不仅派遣大批留学生赴日本学习,而且于1904年颁布“癸卯学制”,又于1905年废除科举制.“中华民国”成立后,国民政府颁布实施较为新式的教育体制——“壬子癸丑学制”,并规定“大学以教授高深学术、养成硕学闳材、应国家需要为宗旨”.[10]这消除了癸卯学制所尊奉的“无论何等学堂,均以忠孝为本,以中国经史之学为基”[11]628的这一封建色彩浓厚的立学宗旨,偏向于学术专业化,并开始建立自己的学术特色.随后,全国各大学陆续建立数学系,现代数学在中国开始逐步发展.

当时大学的数学系教学使用外文教科书的现象非常普遍.这虽然可以使学生直接接触外文原著并有利于学习外文,但对不精通外文的学生来说存在言语障碍,不利于现代数学在中国的本土化和传播.国民政府定都南京后,以蔡元培为代表的学界精英提倡将中国各学校的教科书中国化.[12]江泽涵早年留学美国,跟随其导师莫尔斯(Marston Morse,1892-1977)研究拓扑学,1930年获哈佛大学博士学位,随即应普林斯顿大学的聘请,任拓扑学教授莱夫谢茨的研究助教一年.[13]江泽涵是一位有抱负的数学家.在美国时,他就立志回国后“迅速引进现代数学新理论,坚决终生从事教学与研究”.[14]151931年他回国后,任教于北京大学数学系.同年,他在清华大学开设拓扑学课程,这是中国首次开设拓扑学课程,[15]所用教材是韦布伦编撰的《位置几何学》和莱夫谢茨的讲义[3].1934年,他在北京大学开设此课程,并将沙爱福与施雷发合著的《拓扑学教科书》作为教材,而且是用中英文授课.[13]

1937年7月卢沟桥事变爆发后,北京大学、清华大学、南开大学西迁至长沙,合组为“国立长沙临时大学”.江泽涵以为会在皖南旌德乡下长住,便萌生翻译一本中文拓扑学教科书的想法.正如他在其译著《拓扑学》序中所说:“那时候以为必须在皖南旌德乡下住一个相当长久的时期,就有在乡下翻译一本拓扑学的志愿”.[16]当时他只带了两本书,一本是沙爱福与施雷发合著的《拓扑学教科书》,另一本是亚历山大里亚德夫(Paul Alexandroff,1896-1982)与霍普夫合著的《拓扑学》(Topologie).[13]1938 年,“国立长沙临时大学”迁至云南昆明,更名为“国立西南联合大学”后,江泽涵于1937年开始开设拓扑学课程,[17]所用教材是亚历山大里亚德夫与霍普夫合著的《拓扑学》[18].在后来的教学中,他也用沙爱福与施雷发合著的《拓扑学教科书》作为教本,边教边译.[17]而在他看来,《拓扑学教科书》是一本空前的好书,内容清楚严密,便于初学.[16]于是,江泽涵决定将其翻译为中文的拓扑学教科书.

3 《拓扑学》的翻译情况与影响

江泽涵译著《拓扑学》的底本于1934年在德国首次出版,后于1947年重印.据江泽涵的学生胡炳生和其子江丕权、江丕栋编写的《江泽涵先生年谱》记载,《拓扑学》一书于1947年夏译完,江泽涵在7月为此书作序.[2]由前所述,江泽涵于1937年将底本带到长沙并开始翻译.因此推断可知,《拓扑学教科书》的初版是译著的底本.译著全书共12章87节,中译本目录与德文版一一对应(表1),章节完全一致,内容无删减.译著力求内容与底本一致,底本中涉及的图形和公式以及数学符号表达在译著中都保持不变,只更改了排版,可见其忠实原文的程度很高.

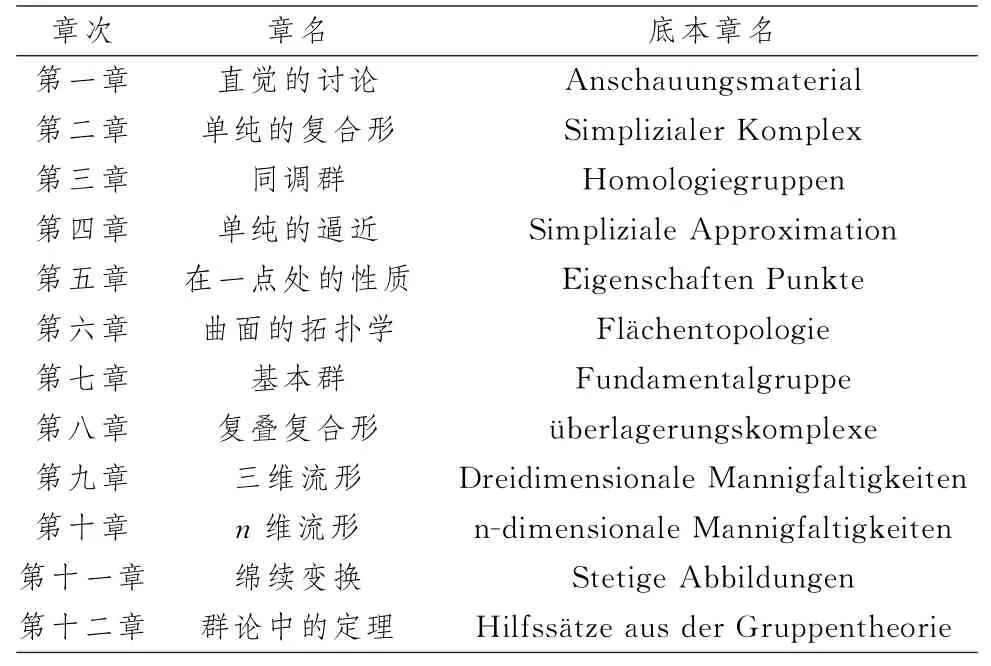
表1 《拓扑学》与底本的对应章次表Tab.1 Catalog of Topology and Lehrbuch Der Topologie table

书籍是沟通知识的桥梁,对译著来说,翻译的精准性尤为重要.科技术语常用的翻译方法有零译法、译意法、译音法、造字法等.[19]“Topology”最早由莱布尼茨于1679年提出,早期称“形式分析学”.[20]后来采用“Topologic”,因为它与地形学“Topography”词意相近,所以也称“形势几何学”或“连续几何学”.[21]江泽涵最早使用“形势几何学”这一名称.“拓扑学”一词是译音法,由姜立夫先生提出,[22]后来一直延续运用至今.

译著《拓扑学》全文用白话文表达,语言简洁明了,叙述通俗易懂.全书排版符合逻辑规律,知识循序渐进.译著《拓扑学》按底本一一翻译,并保留了例题和习题,其在内容和结构上与底本保持高度一致.在此举一例对译著正文内容予以说明,如表2所示.

表2 《拓扑学》凝点定理译文与底本对应内容比较表Tab.2 Condensation point theorem comparison of Topology and Lehrbuch Der Topologie table

名词的译名会影响读者对数学理论的整体把握,同时也影响知识的传播.江泽涵在译者序中写道:“本书中数学名词的译名,多半遵照中国科学社的科学名词审查会于1938年编印的《算学名词汇编》”.[16]《算学名词汇编》[23]中的名词经过科学名词审查会审定,书中名词以英文、法文、德文、日文和中文五种语言对照呈现.译著中的名词大多按此书翻译,基本实现了名词术语本土化.对于首次出现的数学名词,江泽涵在译本中将名词的德语形式标注在其后的括号内,以便读者查阅.《拓扑学》一书名词术语较多,在此不一一列举,经笔者对照,表3的名词是按《算学名词汇编》翻译的.

除表3列举的按《算学名词汇编》翻译的名词外,江泽涵还自译了部分名词.自译方式多样,部分按英语释译,再取相近的数学含义,如底本中的“Basis”,译为“基底”;也有新造术语,如底本中的“Loch”译为“洞”“Lagenraum”译为“位置空间”“Normalunterteilung”译为“法重分”“Umgebungsraum”译为“领域空间”;还有采用组合词来释义的,如底本中的“Simplizialer Komplex”,译为“单纯的复合形”.

从表4可以看出数学名词非一成不变.正如江泽涵在1981年版《拓扑学》的重印说明中写道:“本书中的奇异同调论的处理不仅有失于陈旧,且有缺陷;再者,译本中所用的语句有些也是旧式的,现今已不再选用”.[24]现举部分名词将其与现今释义比较:(1)如译著中的第1章第1节第2页中为了说明同胚的重要性时提到了“全合”,它是几何学中的一个概念,根据后面描述“两个全合的图形本质上无区别”,可知现在定义为“全等”;(2)第1章第4节第25页“绵续函数”的定义是“一个换领域成领域纔(唯一)的变换叫作绵续的变换”,通过与其他拓扑书比较,可知现在称它为连续函数,表示两个拓扑空间之间的一种对应关系,而连续性是数学中非常重要的性质,在此又有了“新”的定义;(3)第3章第24节第123页“闭假流形”的定义与现在“伪流形”一致.除以上所述,不仅数学名词在修订,数学符号也有了变化,例如第2章第9节第50页的“0□n□m”,现在将其表达为“0≤n≤m”更简便.

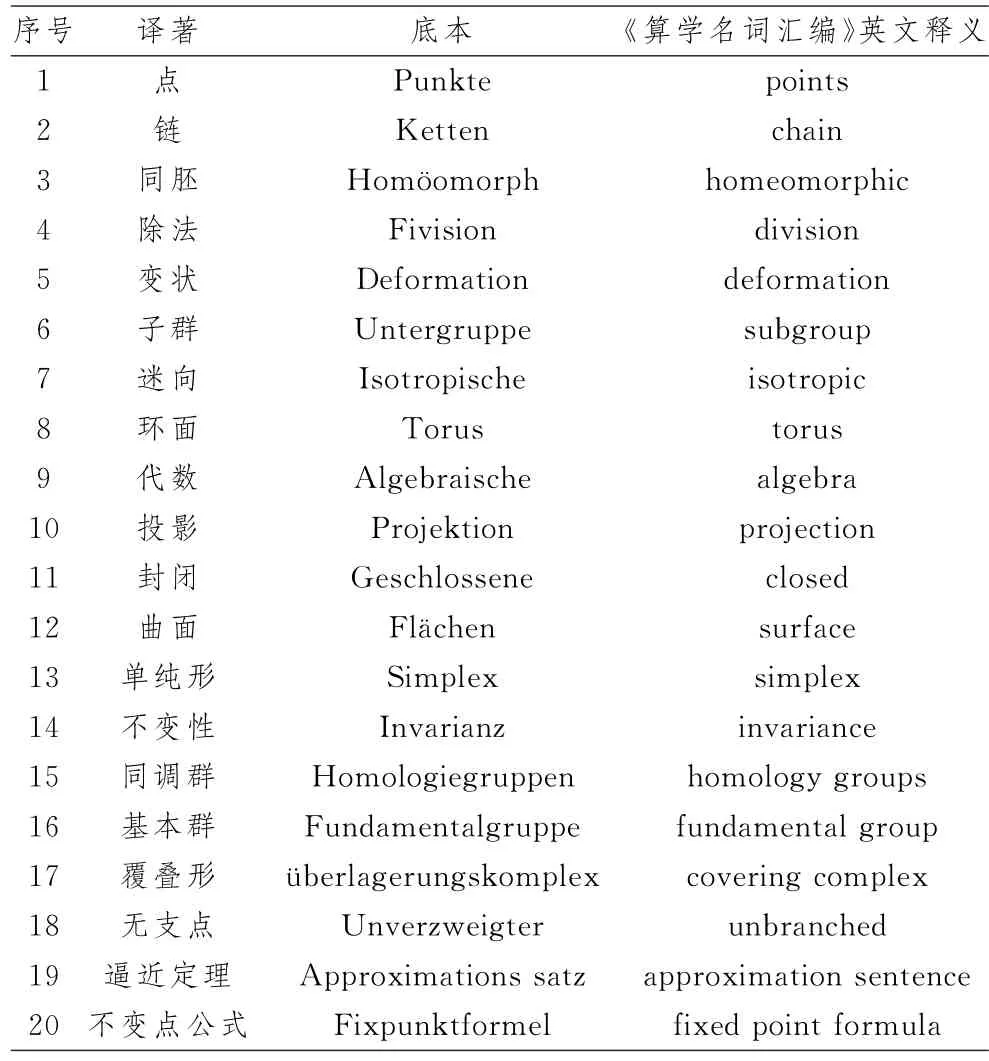
表3 《拓扑学》中按《算学名词汇编》翻译的部分名词比较表Tab.3 A comparison of some terms in Topology translated according to Compilation of Mathematical Terms table

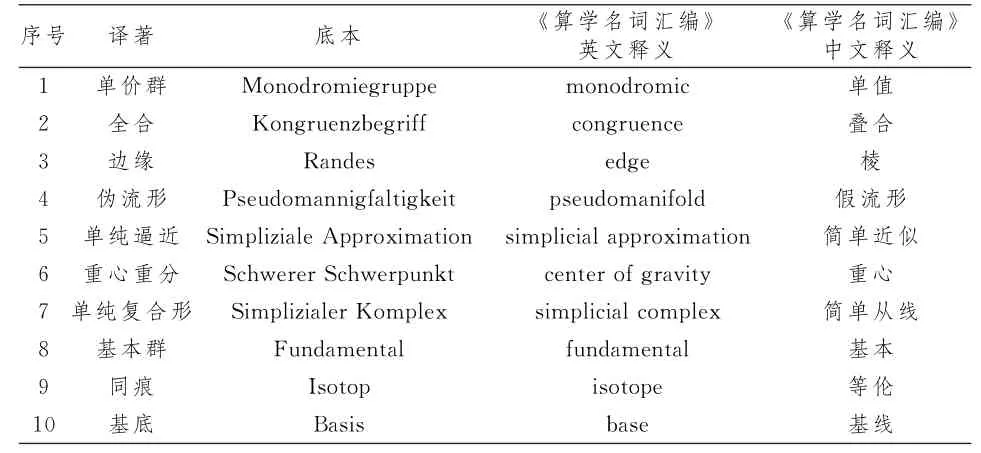
表4 《拓扑学》中未按《算学名词汇编》翻译的部分名词比较表Tab.4 A comparison of some terms in Topology not translated according to Compilation of Mathematical Terms table

译著《拓扑学》注重细节,在某些知识的处理上相对底本更清晰.如底本第4 章第29 节第102 页的“Was nun die Formeln (2)und(4)angelangt,so können höchstens die Vorzeichen falsch sein.Ein Simplex Ekdes Randes von zk+1z.B.muβjedenfalls auf xkoder ykoder einer der Ketten zliegen”,译为“至于公式(2)与(4),至多只有正负号的错误.例如公式(4)中zk+1的边缘中的一个单纯形Ek,就必定是xk中,或yk中,或一个z链中的一个单纯形”,在译文中说明了zk+1的来源,体现了数学的精确性.

第4章第29节第103页的“Koeffizientenvergleichung ergibtηv=ξv=1,womit die Formelon(2)bis(4)bewiesen sind”译为“比较单纯形的系数,即知ηv=ξv=1.因此公式(2),(3),(4)都证明了”.根据前文的叙述已经证明了(3)是(1),(2)与(4)的结果,而这里是为了证明(2)与(4)式的公式是正确的,所以在译文中加上(3)式也被证明了是准确的.

第4章第30节第104页的“Den Fall,dass die zu approximierende singuläre Kette Ak0-dimensionalist,erledigen wir vorweg,da er sich nicht den späteren Betrachtungen unterordnet”,译为“关于k=0的讨论不属于后来关于k ＞0的讨论的范围.我们先行证明在k=0时的逼近定理”,在底本中只指出它不属于后面讨论的0维,没有指明k=0.

《拓扑学》在翻译上平实但仍有不足.如某些备注的名词拼写有误,此处举几例进行说明.如底本第1章第4节第18页的“Bewegungszustände”,译本备注的是“Bewegungszustande”;第1章第5节第23页的“Begrenzung”,译本备注的是“Begrunzung”;第3章第18 节第65 页的“algeb raischen”,译 本 备 注的是“algebraischr”;底本第3章第16节第59页的“Als Basis(§86)kann man die orientierten Simplexe E,benutzen”,译文备注的是“我们能用定向的单纯形作这群的一个基底(Basis,§81)”.而底本中§86才是基底和Abel群的内容,通过比较前后文发现,这里是译文误将“§86”印刷成“§81”.

《拓扑学》中值得注意的还有全文的字体格式.底本共三种字体,正文叙述采用一种字体,书中的定理以及一些需要注意的地方采用另一种字体以示区分,而注释、例题、习题等用小字予以说明.译著保留了这些优点,用不同字体叙述全文以示区别,并对一些内容进行加粗处理,这样可以增加可读性.读者在阅读时可根据自身需求进行取舍,进而提高阅读效率.

《拓扑学》在1947年出版后,于1951年再版,[25]1959年出新一版,[26]1981年又重印[24].江泽涵在北大授课时曾将《拓扑学》作为教科书,且用于他主持的拓扑专门化.[27]吴振德、姜伯驹、[28]刘应明[29]都是当时拓扑专门化的学生.南京大学数学教授周学光在大学毕业后曾自学江泽涵译著《拓扑学》.[29]由此,他掌握了代数拓扑学的基础知识和国外研究文献的内容,这为他今后研究同伦理论奠定了基础.江泽涵在《拓扑学》中自创的一些名词术语后来被部分数学家使用.吴文俊就是其中之一.20世纪50年代,吴文俊的论文《“格拉斯曼”流形中的平方运算》中的名词术语多按江泽涵译著《拓扑学》翻译,并使用了江泽涵自创的“流形”“胞腔”“同调类”等名词.[30]《拓扑学》中“流形”“同胚”“同调”“同伦”“边缘”等名词至今仍在使用.[31]江泽涵在1981 年《拓扑学》重印本说明中指出:“它的内容扼要、丰富,表达清晰、具体,二维曲面与三维以及n 维流形的讨论约占全书三分之一.由于他的这些特点,在他以后出版的代数拓扑学新课本,都在所附的文献表课本栏中提到它.甚至有些人认为它还是最好的课本.因为中文的这类课本很少,所以更有重印这译本的必要.”[24]这些表明《拓扑学》出版后影响较大,对拓扑学在中国的传播和发展起到积极作用.

4 结语

自明末利玛窦和徐光启合译《几何原本》前6卷以降,[32]翻译国外数学书籍成为在中国传播西方数学知识的一条重要途径.至19世纪末,翻译国外数学书籍的主体是来华的外国人以及没有海外留学经历的国人.20世纪初,在国外受过专业训练的中国留学生开始成为翻译国外数学书籍的主要力量.在美国立志“迅速引进现代数学新理论,坚决终生从事教学与研究”[13]的江泽涵就是其中一员.江泽涵选择沙爱福与施雷发合著的《拓扑学教科书》作为翻译对象,不仅与“中华民国”开展后现代数学教育相关,也与蔡元培等学界精英提倡将中国各学校的教科书中国化的大背景联系密切,同时也离不开江泽涵在皖南旌德乡萌发翻译一本中文拓扑学教科书的想法.他认为该书是空前的好书,内容清楚严密,便于初学.

翻译书籍有“信、达、雅”三原则,其最早出自严复《天演论》中的“译例言”.[33]江泽涵的翻译成果《拓扑学》在整体上符合“信”,译者多数采用直译方式且忠实于底本,无任意删减.他还自创四字拓扑术语,使之贴切原文,这也为以后编写教科书提供了参考.关于“达”,其在翻译时兼顾本国情况,将底本做了本土化的处理,使之既准确表达了术语的原意,又符合中文习惯,在译著中也尽可能使用简洁明了的语句.在笔者看来,唯一不足的是“三难”中的“雅”,一方面在于尚无前例,书中的表达需自创,很难做到叙述文雅;另一方面在于数学之精准,要做到文字上的“雅”也并非易事.

江泽涵虽然在翻译过程中受到环境因素的影响,但因在美国留学时习得深厚的拓扑学知识,且精通德文,最终克服困难,历经十年完成此项翻译工作.此项翻译工作开中国数学家翻译国外拓扑学著作之先河,是民国时期现代数学在中国本土化的有机组成部分.其翻译成果《拓扑学》出版后影响较大,对拓扑学在中国的传播和发展起到积极作用,应该是得益于该书底本内容清楚、严密,语言简洁明了,叙述通俗易懂等因素综合作用的结果.不论如何,江泽涵的此项翻译工作是中国数学家从国外引入拓扑学著作的一次成功尝试,反映了他对中国拓扑学教科书建设与拓扑学在中国的传播和发展所做的贡献.

致谢:本文在写作过程中得到了郭金海老师的大力帮助,郭老师在论文选题、撰写及修改过程中给出了恰当的建议,并在笔者遇到困难时悉心指导.在此,对郭老师致以衷心的感谢!