充分利用“数形结合”，引导学生理清算理

陈清传

[摘要]如何让计算更有数学味道，要从理解算理开始，但对于以具体形象思维为主的小学生来说，计算算理的抽象性又使学生难以理解，这就需要有一种介于抽象和直观之间的媒介来解决，“数形结合”是最有效，最直观的办法，它可以将“数”体现于“形”，又可以用“形”体现出“数”的作用，使学生体会到“数”与“形”的关系，将抽象的语言与直观的图像联结起来，使计算的道理直观化。其实在教材中应用了不少“数形结合”的工具，比如点子图、数格子、摆小棒、画数线等，本文探讨了如何有效地利用这些直观方法，帮助学生主动参与到表象的建立和算理的探究中，从而达到对算理的深层理解，牢固掌握算法，形成计算技能。

[关键词]“数形结合”;算理;探究;理解

“算理”，字面的理解就是计算的道理，为什么这样算的理由。在小学数学计算教学中，有的学生虽然懂得算，但却不知道为什么这样算，也就是对算理不甚了解，只知其然，不知其所以然，很多学生的计算只是机械地操练，学生的计算能力整体偏弱。

一、趣摆小棒，感悟算理

小棒是孩子们眼中非常熟悉的物品，既直观又形象，是教材最常采用的教学方法之一。小棒好比是一把打开数学大门的“金钥匙”，实践证明，巧妙地运用“摆小棒”操作活动，能使抽象的计算具体化、深奥的算理形象化，又能使数学学习变得有趣。

如教学北师大版一年级上册“一共有几瓶牛奶（9+5=？）”时，一般学生都能正确得出14这一结果，但是教学9+5的目的不仅仅是让学生口算得出结果，更重要的是要引导学生展现“凑十法”的思考过程，明白加法的计算规律。特别是低年级学生，合理有效地引导学生利用常见的小棒这一学具，“数形结合”显得既有必要又有趣味。

教师引导学生分步、有序地操作：

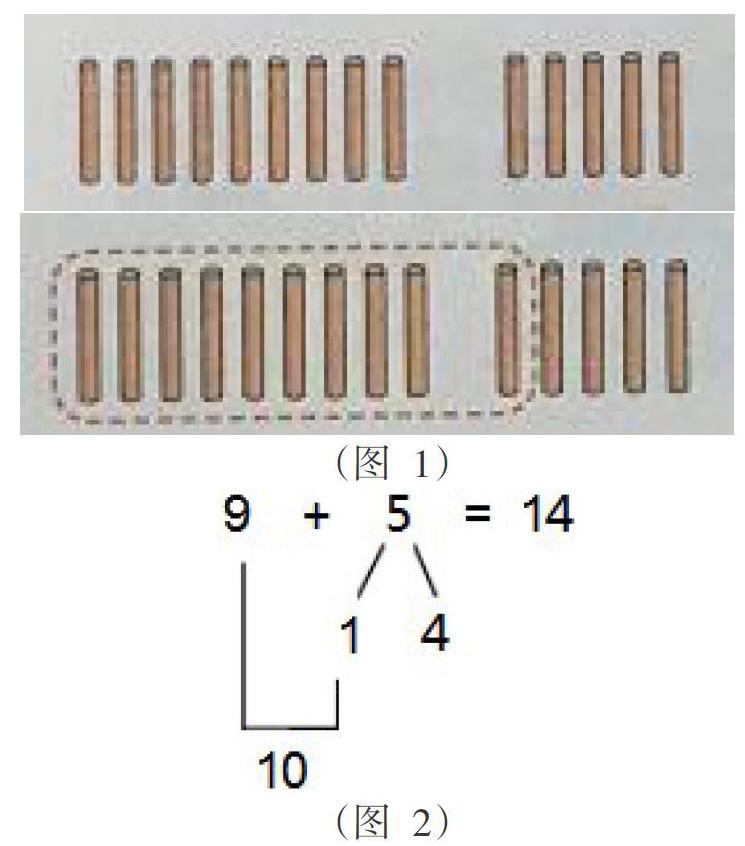
1、照算式中的数摆2堆小棒，一堆9根，另一堆5根。提出问题思考：怎样操作，让人一眼就看出有14根小棒？

2、边操作边口述，把5分成了1和4，再把1和9凑在一起得到10，10和4合起来共14根（图1），再指定学生上台现场操作，边操作边口述，其他学生认真倾听。

3、在学生摆小棒这一操作探究的经验基础上，教师利用课件动态展示从5中“分”出来的1根小棒和9根小棒“合”凑成10的过程，概括出“凑十法”，明白计算的道理（图2）。

有的教师可能会认为学生都会算了，还摆小棒会造成秩序混乱，浪费宝贵的教学时间，可以省去操作过程，不用再让学生操作小棒。其实“摆小棒”是一种行为操作，以直观的方法获得计算经验和计算结果，是学生获取直接经验的重要渠道，学生在操作的过程中理解“凑十法”的整个思考过程。所谓“我经历了，我就懂了”，学生有了这种操作的经历，会在脑海中形成直观的印象，当下次教学8加几，7加几时，头脑中就会自觉地再现“凑十法”的操作过程，从而达到培养迁移类推能力的目的。

二、妙用点子图，探究算理

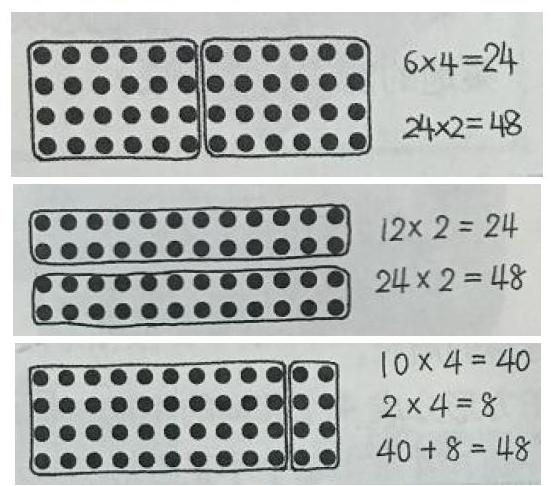
点子图也是教材常用的引导学生理解算理的一种教学方法，教材为什么要用点子图？教材中提到：低年级学生的思维正处在由形象思维向抽象思维过渡的阶段。点子图是从形象思维到抽象思维的数学化过程，妙用“点子图”的直观载体帮助学生更好地理解算理、开拓学生的思路，让学生能够运用多元化的思维解决数学问题，有效提高学生理解问题的能力。例如教学北师大版三年级上册“一共有多少只蚂蚁（两位数乘一位数）12x4”计算时，提供给学生一张点子图为研究素材，让学生自己动手操作，在点子图中充分暴露思维轨迹，呈现丰富的思考过程，体会不同的解题策略和个性理解。学生交流算理时，始终结合点子图来解释明理。

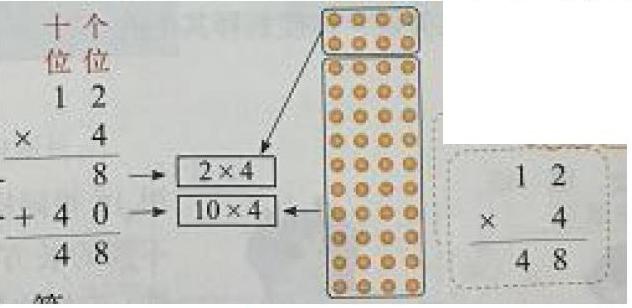
在利用点子图充分理解口算算理的基础上，教材继续用点子图来突出竖式加法里面两个加数的意义，也揭示了竖式笔算两个重要的计算步骤与口算的联系。

学生通过观察点子图理解8和40分别在点子图中的哪个位置？理解竖式表示的算理是先把12看成10和2，4x2=8表示每排有4只，2排，就是2个4有8只蚂蚁，10x2=40是每排有4只，10排表示10个4，共40只蚂蚁，再加起来一共有48只蚂蚁。针对“4”为什么要写在十位上，8写在个位上，继续引导学生在图中找到它所表示的点子数并说清理由。最后学生通过对比明白了两种写法的道理其实是相同的，即：都是用一位数分别去乘另一个因数的每一位，再把所得的积相加，只是第二种写法比较简洁。

探索算理是为了更好地掌握算法，有数与形的巧妙结合，就能化抽象为直观地理解算理。在点子图的几何直观下能更好地把乘法意義从隐性转化为显性，为学生更好地理解搭建“脚手架”，直观地解释每一步的算理，沟通了口算和竖式计算相应的联系，“先分后合”的思路与乘法竖式计算的基本思路融为一体，突出了教学重点，突破了教学难点。

三、利用数线，理解算理

数线作为一种直观工具，能帮助小学生理解数学算理。北师大版教材从一年级就开始引入数线，类似“尺子”的数线实际上是数轴的“雏形”，利用数线既可以体会数的顺序和比较大小，又可以进行计算：“顺着数”相当于加法，“倒着数”相当于减法，可以帮助学生很好地理解加法和减法的计算道理，因此，数线具有重要的价值。在教学北师大版二年级《加与减》中有关三位数进位或不进位加减法时，如计算122+149=？，这里教材采用了画数线、拨计算器、列竖式计算三种方式，启发学生借助多种直观方式获得计算结果。在画数线时把122作为起点，将149分为100、40、9，因为是加法所以“向右顺着画”，先整百加，再整十加，最后加个位得出271的结果。计算118-57时，118作为起点，因为是减法所以“向左倒着画”，整十、个位逐一减去，非常地直观易懂。

经过实践，学生很喜欢这种方式，学生更容易依据数线理解算理得出结果，而且不易出错。数线是一种非常直观易懂的方法，等同于分步计算，学生容易理解数的组成和意义，发现相同数位要对齐的计算道理。教材之所以大量采用画数线的方法解决加与减的计算就是因为画数线体现了口算过程的直观化，它帮助学生直观地展示和记录了计算的过程，利于学生数感的形成。当然，对于计算教学，教材还采用了很多直观的方法，如表格、画线段、计数器等，主要目的就是要让学生在领悟算理的基础上掌握算法，形成计算技能。不明白算理的算法是机械的，对计算技能的形成是不牢固的，其迁移能力就难以培养，无法灵活运用。在计算教学要充分发挥这些直观工具，注重“数形结合”帮助学生理解算理，做到“循理入法，以理驭法”，最终形成牢固灵活的计算技能。