追本溯源 深度建构

王庆菊

[摘要]深度学习强调批判理解、内容整合、知识建构、问题解决、能力提高和思维发展。在深度学习背景下的数学复习课中，通过思维导图，提高學生的单元知识再加工能力和建构知识网络的能力;通过追本，唤醒学生已有的经验;通过溯源，厘清知识的来龙去脉，促进学生对知识本质的深刻理解以及对知识之间内在结构的深度把握，将思维与实践引向更深更远处。

[关键词]追本;溯源;建构

[中图分类号]

G623.5

[文献标识码]A [文章编号] 1007-9068（ 2020）11-0009-02

“平面图形的面积”是六年级下册总复习“空间与图形”中的一节课，它是在学生已经学习了长方形、正方形、平行四边形、三角形、梯形、圆的面积计算的基础上进行教学的。教材首先是小精灵提问：“说说什么是平面图形的面积。”接着通过图示，要求学生写出各个图形的面积计算公式，并说一说这些计算公式是怎样推导出来的。不难读出编者的意图：一方面让学生明确平面图形面积的意义，掌握长方形、正方形、三角形、梯形、圆等基本平面图形的面积计算公式及其推导过程;另一方面，借助图示引导学生构建平面图形面积的知识网络，体验各平面图形之间的关系，形成知识体系。那么，平面图形面积计算的本质是什么？平面图形面积计算的根与源在哪里？长方形、平行四边形、三角形、梯形、圆的面积计算之间有着怎样的内在统一性？面积学习的背后，更为深层的价值又是什么？

【教学过程】

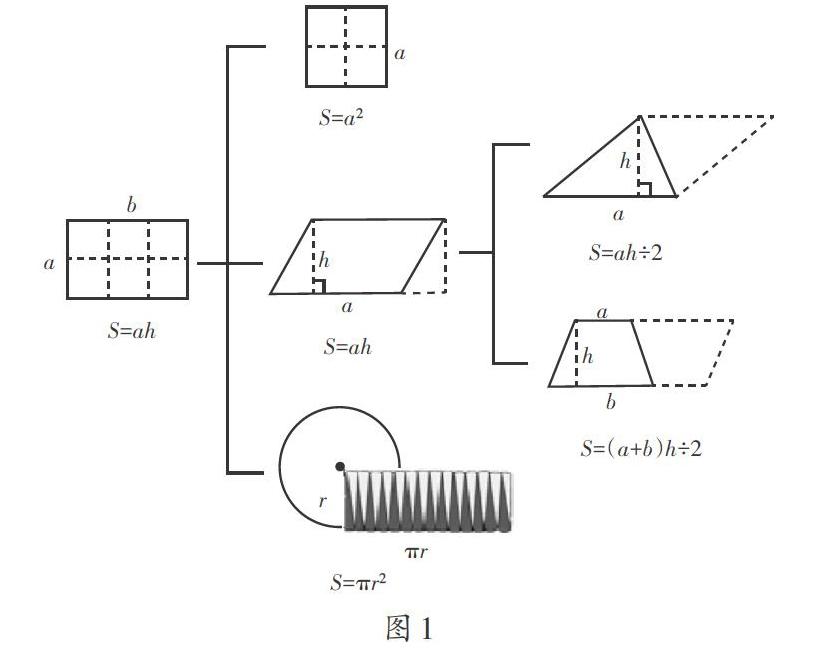
出示学生整理的平面图形的面积计算公式及其推导过程（如图1）。

1.沟通联系

师：能说说为什么这样整理吗？通过整理这些图形面积的计算方法，你有什么发现？

生1：这六种平面图形之间联系很紧密。

生2：从左往右看，根据左边图形的面积计算公式可以推导出右边图形的面积计算公式;从右往左看，在研究一种新的图形的面积计算方法时，都是把它转化成已经学过的图形。

师：以前我们是一个图形一个图形学习的，今天把它们放到一起，就能发现它们之间的联系。（逆时针转动图1）换个角度看这幅图，你觉得这幅图像什么？

生3：像一棵大树。

师：这个说法很形象！这是一棵知识的“大树”，树根是谁？

生4：长方形的面积计算公式。

师：这样看来，哪个图最关键？

生5：长方形。

师：是呀，长方形是基础，知道了长方形的面积计算方法，我们就可以推导出许多图形的面积计算公式，而连接这些图形的正是“转化”这一重要的思想方法。

2.深度建构

师：再看这幅图，你有问题要问吗？

生6：其他图形的面积计算公式可以做“树根”吗？比如平行四边形或者三角形、梯形、圆形。

学生小组讨论后汇报：

平行四边形可以做“树根”：把长方形、正方形、梯形、圆转化成平行四边形。

三角形可以做“树根”：把长方形、正方形、平行四边形分割成两个完全相同的三角形;把梯形分割成两个三角形;把圆剪拼成近似的三角形。

梯形可以做“树根”：把长方形、平行四边形分割成两个完全相同的梯形;把梯形分割成两个三角形。

圆形可以做“树根”：把长方形、平行四边形剪拼成近似的圆形。

师：既然这样，你能只用一个公式就计算出长方形、平行四边形、三角形、梯形、圆的面积吗？

生7：我认为这六种图形中的任何一个都行。

师：如果由你来编写教材，你会按什么顺序安排这几个平面图形的面积学习？

生7：我会按照平行四边形、三角形、梯形、长方形、正方形、圆的顺序编写。

生8：我会按照三角形、平行四边形、长方形、正方形、梯形、圆的顺序编写。

生9：我会按照梯形、平行四边形、三角形、长方形、正方形、圆的顺序编写。

生10。：我会按照圆、长方形、正方形、平行四边形、三角形、梯形的顺序编写。

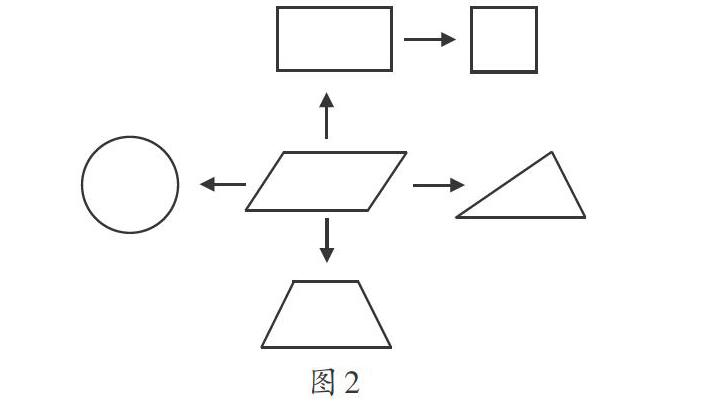
生11（出示图2）：我会按这幅图的顺序编写。

师：课本上一直是按“先长方形，再平行四边形、三角形、梯形、圆”的顺序来研究，这又是为什么？

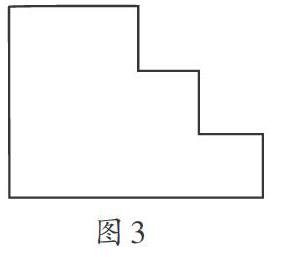
师：现在让我们穿越到三年级，回到最初的面积计算。假设你现在是一名三年级的小朋友，所有图形的面积公式你都不知道。（出示图3）怎样知道这个图形的面积有多大？

生12：我觉得可以用面积单位来摆一摆，看看这个图形里有多少个面积单位，它的面积就是多少。

师（出示图4）：的确，最初没有计算公式时，我们就是用面积单位来度量的。不过，面积单位是什么图形？

生13，：边长为1厘米或1分米、1米的正方形。

师：既然这样，用面积单位摆一摆的方法测量图形面积时，哪种图形的面积更容易测量？

生14：长方形和正方形。

师：对。正如华罗庚爷爷所说，“量，起源于量。”你知道这句话是什么意思吗？

生15：我的理解是，比如像长度、面积、重量等这样的量，都是用度量单位测量出来的。

生16：我明白了！长方形的面积能直接用面积单位来测量，而平行四边形、三角形、梯形、圆这几个图形的面积不能直接用面积单位测量出来，所以我们先学习的就是长方形的面积。

子日：“温故而知新”，然“复习课难上”却是许多教师经常感叹的。复习课既不像新授课那样有“新鲜感”，又不像练习课那样有“成就感”，“复习课就是回忆概念、公式，重复做以前做过的题”。那么，复习课，尤其是总复习课该如何“温故”，又该如何“知新”？

1.温故：追本溯源

复习课的基本任务在于“理”与“通”，即系统整理、融会贯通。长方形、平行四边形、三角形、梯形、圆的面积计算方法是什么？这些图形的面积计算之间又有着怎样的内在统一性？平面图形的面积的学习从三年级开始，一直持续到六年级，时间跨度大，知识点比较分散。上述教学通过“追本”，唤醒学生已有的面积计算经验;通过“溯源”，沟通不同图形面积计算之间的逻辑关联，厘清知识的来龙去脉，让零散的知识一一再现并形成条理化、系统化的树形结构图，增强学生对平面图形的面积的整体认识，使得转化思想得到进一步的彰显。

2.知新：深度建构

复习课的基本任务还在于“发展”，即知识得到新的生长、学生得到新的发展。面积学习的背后，更为深层的数学思想又是什么？面积是最基本的几何学概念，面积的大小就是看一个面包含有多少个面积单位。上述教学凭借层层递进的问题串，在迂回中杀了个漂亮的“回马枪”：其他图形的面积计算公式可以做“树根”吗？你能只用一个公式就计算出长方形、平行四边形、三角形、梯形、圆的面积吗？如果由你来编写教材，你会按什么顺序安排这几个平面图形的面积学习？课本上一直是按“先长方形，再平行四边形、三角形、梯形、圆”的顺序来研究，这又是为什么？……一系列问题接踵而至，直逼教材，学生在“诘问——批判——重构”中一次次突围，获得对知识本质的深刻理解以及对知识之间内在结构的深度把握。长方形、平行四边形、三角形、梯形、圆的面积计算之间的网状沟通在多种可能中不断地卷入、强化，在度量的本质意义中凸显了面积单位的重要性以及长方形的面积作为平面图形面积研究的核心地位，使学生在深度思辨中拾阶而上。这样，不仅实现了知识本质上的融合，而且能促进学生把问题想深想透，将思维与实践引向更深更远处。

复习是学习之母，复习是为了更好地出发。在追本溯源中深度建构，是一种理念，更是一种信念;是一种境界，也是一种行动。它超越当下，穿越时空，能给数学学习带来无限的生机与活力。

【本文系河南省基础教育教学研究项目“小学数学深度学习实验研究”的研究成果。】

（责编金铃）